爆破荷载下岩质直立边坡预应力锚板墙动力响应机理

靳晓波，孙金山，高振鲲，聂 峥

（1. 北京城建勘测设计研究院有限责任公司，北京 101100；2. 中国地质大学（武汉），武汉 430074）

预应力锚板墙是近些年利用锚杆技术形成的一种新型挡土结构[1-2]，它自身结构质量轻，使挡土墙的结构轻型化，与常见的重力式挡土墙相比，可节约大量的误工和节省工程投资，并且利于挡土墙的机械化、装配化施工，可以减轻繁重的体力劳动，提高生产率；可采用自上而下逐级施工的方法，不需要开挖大量基坑，能克服不良地基挖基的困难，可以有效地避免边坡坍塌，并利于施工安全。锚板墙的一端与工程结构物联结，另一端通过钻孔、插入锚杆、灌浆、养护等工序锚固在稳定的地层中，以承受土压力对结构物施加的推力，从而利用锚杆与地层间的锚固力来维持结构物的稳定。此种围护结构由挡土结构与锚固系统两部分组成，由挡土结构与锚固系统共同承担土压力。挡土结构常采用钢筋混凝土墙面（肋柱、面板）、排桩加止水帷幕或地下连续墙，支撑体系常采用土层锚杆，锚杆将桩、墙等挡墙所承受的荷载通过拉杆（索、管、栓）传递到稳定土层中，形成锚杆体系，锚固体系可分为锚杆式和地面拉锚式两种。随基坑深度不同，可分为单层锚杆、二层锚杆和多层锚杆。

边坡支护结构的工作机理非常复杂，影响因素众多，目前有关边坡支护结构在天然地震和爆破地震等动力作用下的响应特性和工作机理的研究，在数值模拟、试验和理论计算方面已初步取得一些成果：李宁等[3]利用数值仿真试验研究了不同爆破单响药量、不同岩体阻尼比及距爆区不同距离不同预应力吨位的预应力锚索的动态响应特性，得到了关于单锚、群锚的动力响应规律的量化规律。汪鹏程[4]通过建立一切方直立边坡模型开展了地震荷载作用下桩锚支护土坡动力响应研究；Bathurst和Ho等[5-6]对锚杆挡墙的动力响应进行了有限元模拟；单仁亮等[7-8]用物理模型试验研究了集中装药荷载作用下临近工作面端锚锚杆的动态响应；Ivanovic等[9-10]对单根预应力锚杆在动载作用下的动力响应特性开展了系统的物理试验并通过数值模型计算取得了较为显著的成果；陆遐龄、张云等[11-12]根据工程施工中的现场试验，研究了爆破荷载对边坡预应力锚索等锚固设施的影响；董建华等[13-15]通过建立边坡支护结构的水平地震动力计算模型求解出水平地震作用下土钉和锚杆的动力响应解析解，并通过有限元软件验证了理论计算的合理性，为框架预应力锚杆和土钉边坡支护结构的地震分析及抗震设计提供了理论依据。

现阶段有关预应力锚板墙的动力分析还较少，无法满足工程实践的需要。为了更好地指导今后类似工程设计与分析，开展板预应力锚板墙边坡支护结构的动力特性分析是非常必要的。笔者结合重庆市沙坪坝区的沙坪坝铁路枢纽综合改造工程，分别对不同的锚杆预应力、锚固段长度等参数进行了敏感性研究，得到了一些初步量化规律，研究结果可以为预应力锚板墙边坡支护的安全设计及优化提供一定借鉴。

1 岩质边坡模型概化

1.1 计算模型

重庆市沙坪坝区的沙坪坝铁路枢纽综合改造工程基坑开挖范围南北宽125 m，东西长540 m，开挖面积约5.4×104m2，开挖方量约1.36×106m3。本基坑工程的开挖面积较大、边坡较高，基坑平均深度超过30 m，属于深基坑，基坑紧邻铁路站台、重庆八中、翁达平安大厦等重要建筑，周边环境较窄，施工安全等级为一级，地层由砂岩、泥岩、黏土所构成，可以提供较大的锚固力。通过对上述方案的比较以及对基坑的具体情况的分析，选取预应力锚板墙作为主要支护结构。

本文选取风井基坑西侧与原地面及地铁站台层之间的基坑边坡为研究对象建立基坑边坡数值计算模型。计算过程中，视岩体为各向同性均质介质，采用弹塑性本构模型和摩尔—库伦破坏准则。计算尺寸取30 m×24 m×2 m，除临空面外其余设置黏滞边界，防止波在边界上的反射。在高程236.50～253.50 m处设置预应力锚板墙，板墙墙高17.0 m，自上而下设置预应力锚杆，支护结构立面及剖面如图1、2所示。计算中模型岩体采用实体单元模拟，板墙用壳型单元模拟，预应力锚杆采用锚索单元模拟。模型的具体计算参数见表1、表2。

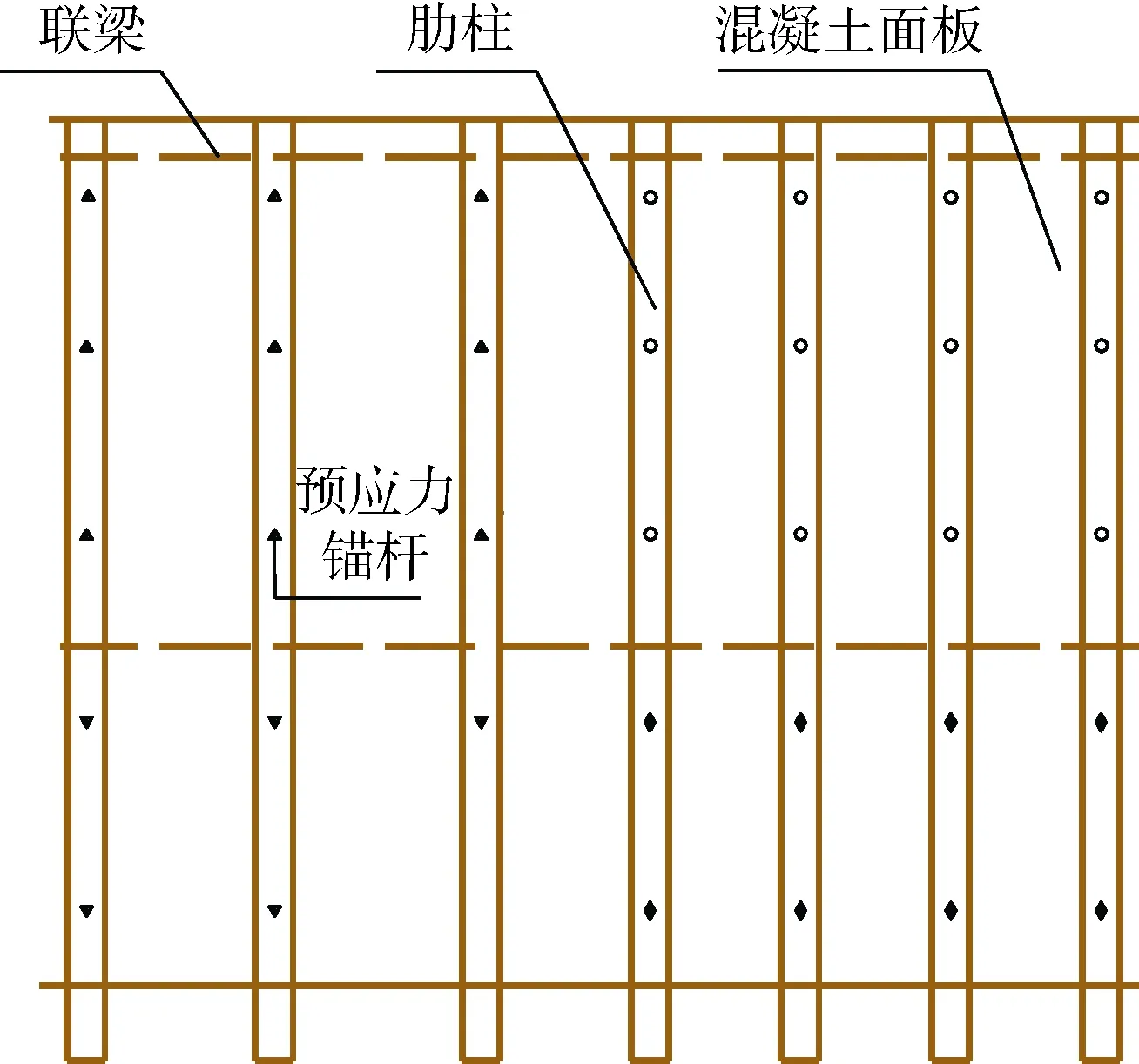
图1 预应力锚板墙支护结构立面Fig. 1 Elevation drawing of the pre-stress anchor wall

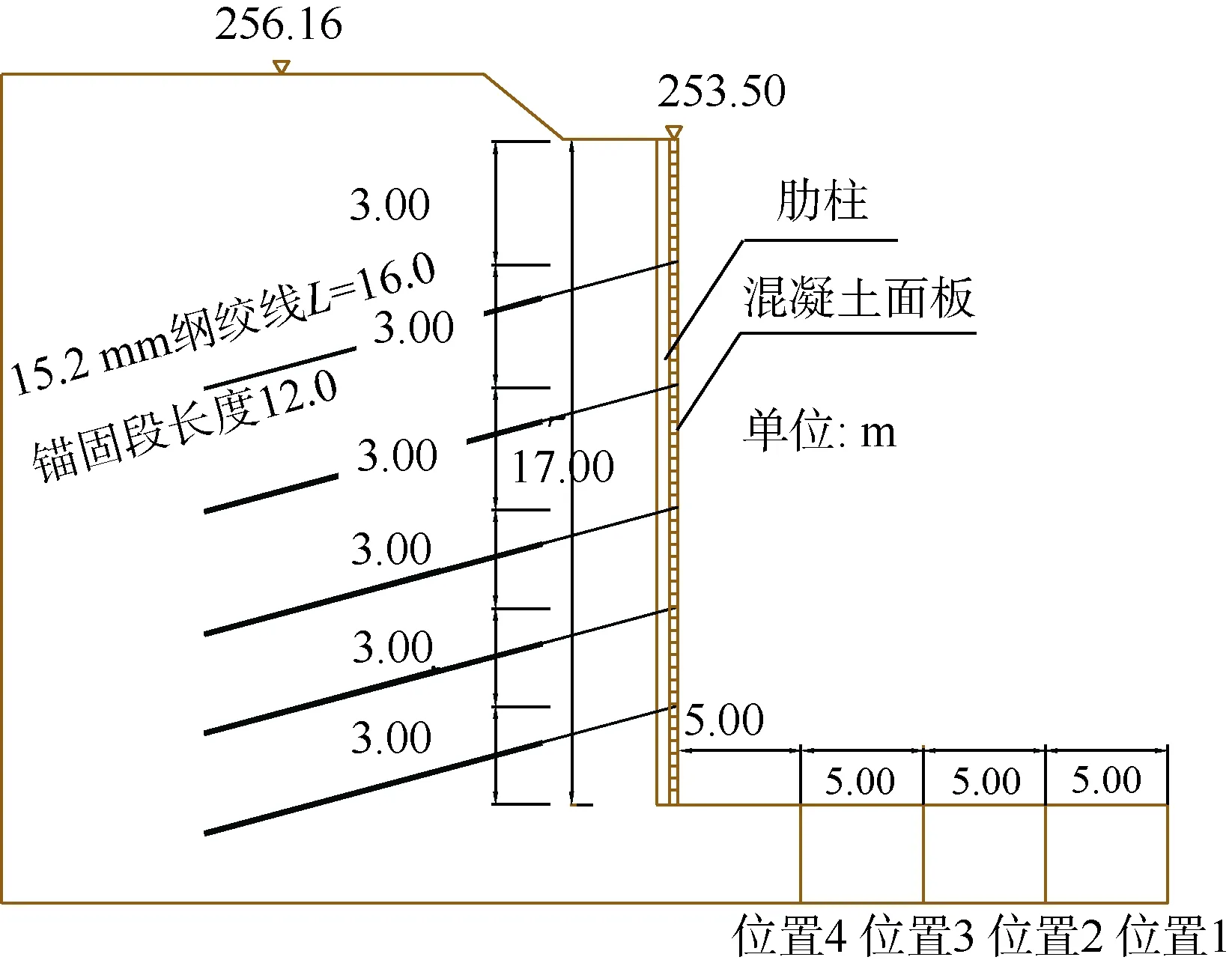
图2 预应力锚板墙支护结构剖面Fig. 2 Profile of the pre-stress anchor wall

表1 土体物理性质Tab. 1 Slope rock parameters

表2 预应力锚板墙设计结果Tab. 2 Design results of the pre-stress anchor wall

1.2 动力输入

爆破动力荷载的确定是进行爆破荷载下岩石边坡动力响应研究的关键。数值模拟中，爆破动力荷载采用现场实测的爆破振动速度时程曲线输入，在图2中4个爆破位置分别施加如图3所示的现场实测爆破地震波，进行爆破作用下的边坡支护结构动力响应分析，并在坡面每根锚杆锚头及锚杆所在点板墙位置设置5×2=10个测点。

图3 现场实测的水平振动速度时程曲线Fig. 3 Time history of the horizontal velocity obtained by site monitoring

2 模拟结果及分析

2.1 锚杆轴力增量响应规律

在地震作用下，锚杆支护边坡内各个质点会产生惯性力，由于地震的竖向和水平向作用，这个惯性力可以分解为水平惯性力和竖直向惯性力，同时锚杆本身又会产生地震附加动应力。一般认为，锚杆所受的拉应力由两部分组成：一部分是由于边坡的变形使锚杆产生的静态拉应力；另一部分为附加动态拉应力。当地震作用消失或者爆破冲击完成后，锚杆支护结构中锚杆的应力又恢复到静态拉应力。

图4为各根锚杆沿杆长方向轴力增量分布曲线，可以看出，爆破作用下锚杆轴力增量分布与静力作用下相似。各根轴力增量在自由段变化不大，从锚固端开始轴力增量急剧减小并都逐步趋于零，且由各部位锚杆轴力分布曲线可知锚杆轴力增量随着爆源与基坑位置距离的减小而逐渐增大，但是增幅越来越小。综合图4中各根锚杆最大轴力增量进行分析，可得到各根锚杆在爆破作用下最大轴力增量随边坡高程的分布情况，如图5所示。由图可知，锚杆轴力增量沿高度基本呈上下小、中间大的分布形式，在爆破作用下位于边坡中部位置的锚杆轴力增量最为显著，上下部锚杆增量较小，呈现出“鼓胀型”分布形式。

2.2 板墙水平位移响应规律

板墙在爆破产生的土压力作用下向临空面一侧产生水平位移，锚固在板墙上的预应力锚杆，由于板锚之间的互相作用，就会限制板墙的水平位移。板墙水平位移沿边坡高程分布曲线如图6所示，由图可知，不同爆破位置工况下板墙水平位移曲线近似呈三角形“鼓肚”状变化形式，最大水平位移出现在板墙中部位置，这与锚杆轴力增量最大值位置基本相同，并且板墙底部在爆破荷载下会有轻微的内倾，这可能是由于爆破对正前方板墙产生的冲击作用所致。

2.3 板锚变形协调分析

板锚结构变形协调条件是板肋式锚杆挡土墙设计中内力计算的关键点。锚杆伸长量和锚杆所在点板的水平位移之间存在变形协调条件。锚杆的伸长量Δi与板在此锚杆点的水平位移Fi沿锚杆方向的分量相等，即Δi=Ficosβ，见图 7。

图4 锚杆轴力增量沿杆长分布曲线（H代表距坡顶距离）Fig. 4 Anchor axial force increment along the bolt(H represents the distance from the top slope)

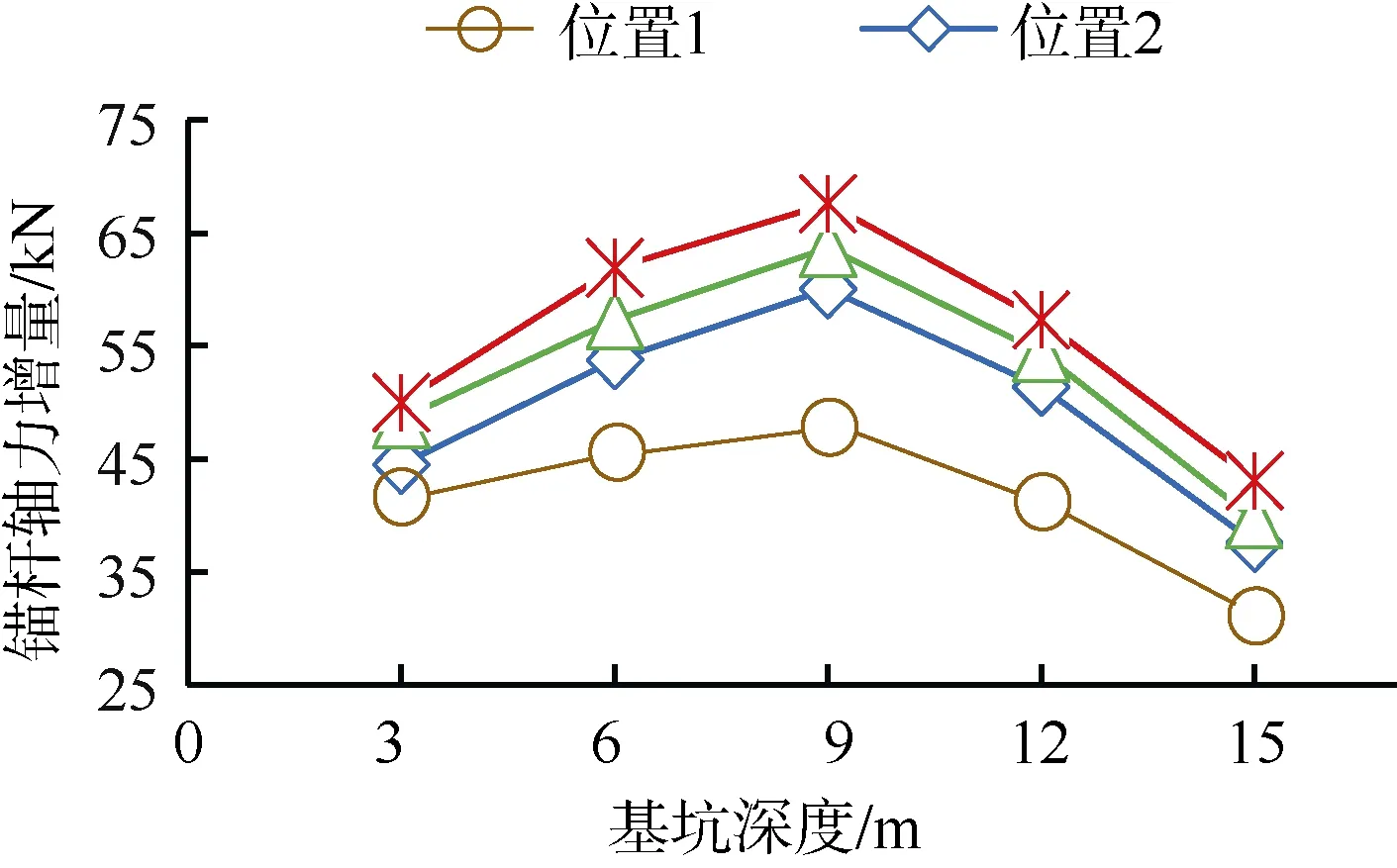
图5 锚杆最大轴力增量随边坡高程分布曲线Fig. 5 Maximum anchor axial force increment along the slope

图6 板墙水平位移沿边坡高程分布曲线Fig. 6 Horizontal displacement of the wall along the slope

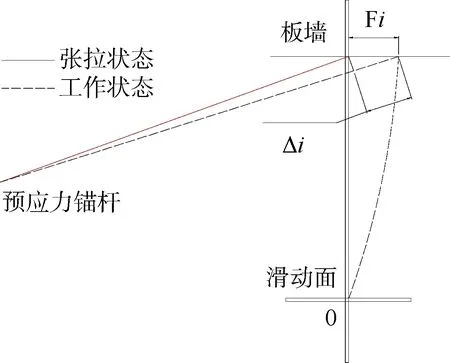
图7 锚板变形协调示意Fig. 7 Compatible distortion between the anchor and the wall

设板墙上共设置n排预应力锚杆，由位移变形协调原理，每根锚杆伸长量Δi与该锚杆所在点板墙的位移Fi在锚杆受力方向的分量相等，即

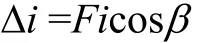
而锚杆伸长量理论计算公式为Δi =PL/EA。式中：L为钢束的有效长度，自锚固端至张拉锚具之间的距离；P为张拉应力，理论伸长量对应的是理论应力，实际伸长量可以反算出实际应力；E为钢材的弹性模量；A为钢材的断面面积。表3给出了爆破作用下，预应力锚板墙支护结构板墙水平位移数值模拟值和理论计算值，由表3可见，板墙水平位移数值模拟和理论计算结果十分接近且偏差控制在 10%以内，说明板—锚结构变形协调较为一致，两者互相作用良好。

表3 板墙水平位移值Tab. 3 Horizontal displacement of the wall

3 参数敏感性分析

基于以上研究成果，仍以前述沙坪坝模型尺寸为研究对象，本节利用FLAC3D分析了锚杆预拉力大小、爆破荷载振动峰值和锚杆锚固段长度对锚杆轴力增量和板墙水平位移的影响，得到了每根锚杆和板墙上部、中部和下部的一些变化规律。

3.1 预拉力

为了分析锚杆预应力大小对爆破作用下锚杆轴力增量和板墙水平位移的动力响应，选取预应力从50～550 kN进行分析计算，得到预应力大小与锚杆轴力增量和板墙水平位移关系曲线，如图8、图9所示。由图8可以看出，随着锚杆预应力的增长，各根锚杆在爆破作用下轴力增量越来越低，其中第1、2、3、4、5根锚杆轴力增量分别下降了30%、27%、21.6%、19.5%和 24%，各根锚杆的轴力降低较为一致，这说明提高预应力在一定程度上有助于降低锚杆对爆破的振动效应。由图9可知，板墙各部位位移随着预应力的增大而逐渐降低，在桩顶、桩中和桩底部水平位移分别降低了51%、46%和77%，桩底部的位移较其他位置减小更为显著，也从另一方面证明了增大预应力降低爆破作用对于支护结构的影响效果的有效性。

3.2 爆破峰值荷载

模拟计算结果显示，在其他参数保持不变的情况下，锚杆轴力增量和板墙水平位移的动力响应呈现非线性变化特征。如图10、图11所示为当爆破峰值荷载分别取为1～10 MPa时，边坡支护结构锚杆轴力增量和板墙位移变化曲线，主要呈现如下特征：

图8 不同预应力条件下锚杆轴力增量变化曲线Fig. 8 Axial force increment under different prestresses

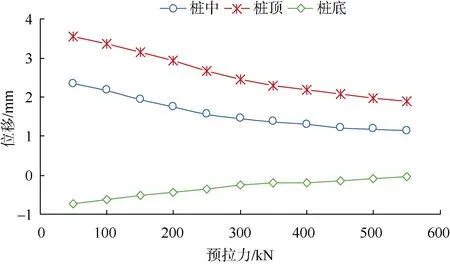
图9 不同预应力条件下板墙水平位移变化曲线Fig. 9 Horizontal displacement under different prestresses

图10 不同荷载条件下锚杆轴力增量变化曲线Fig. 10 Axial force increment under different blast loads

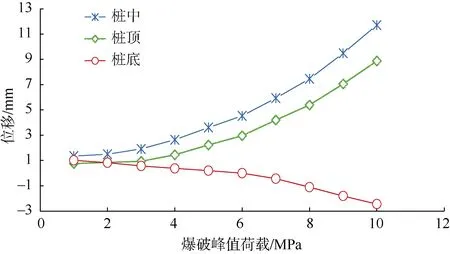
图11 不同荷载条件下板墙水平位移变化曲线Fig. 11 Horizontal displacement under different blast loads

1）当爆破峰值荷载在1～3 MPa区间时，各根锚杆轴力增量和板墙各位置水平位移随荷载变化基本一致，均较为缓慢，其中第2根锚杆的轴力增长最为明显，其次为上下两侧，最上和最下部分锚杆轴力增长较小；板墙水平位移最大处与锚杆轴力增长最大处几乎在同一位置，底部板墙出现一定的内倾。

2）当爆破峰值荷载在4～10 MPa区间时，各根锚杆轴力增量和板墙各位置水平位移随荷载变化基本一致，均抛物线状迅速增大，且各根锚杆轴力增量和板墙水平位移的增大幅度较为接近。

由此可见，在爆破作用下，各根锚杆轴力增量和板墙各位置水平位移的变化规律具有一定的荷载敏感区间，即荷载频率较低，大致在1～3 MPa时，荷载峰值对边坡支护结构影响较大；而荷载峰值超过3 MPa后，即在3～10 MPa时，荷载峰值对边坡支护结构影响越来越显著。

3.3 锚固段长度

根据相关研究成果，在锚杆杆体总长度一定的情况下，减小内锚固段长度，可有效控制杆体轴力的增大。设置预应力锚杆总长为20 m，分别取锚固段长度L=11、13、14、15、16 m时，研究边坡支护结构在爆破作用下的动力响应，并分别绘制锚杆轴力增量沿锚杆全长、板墙水平位移沿板墙全长之间的关系曲线，如图12、图13所示。

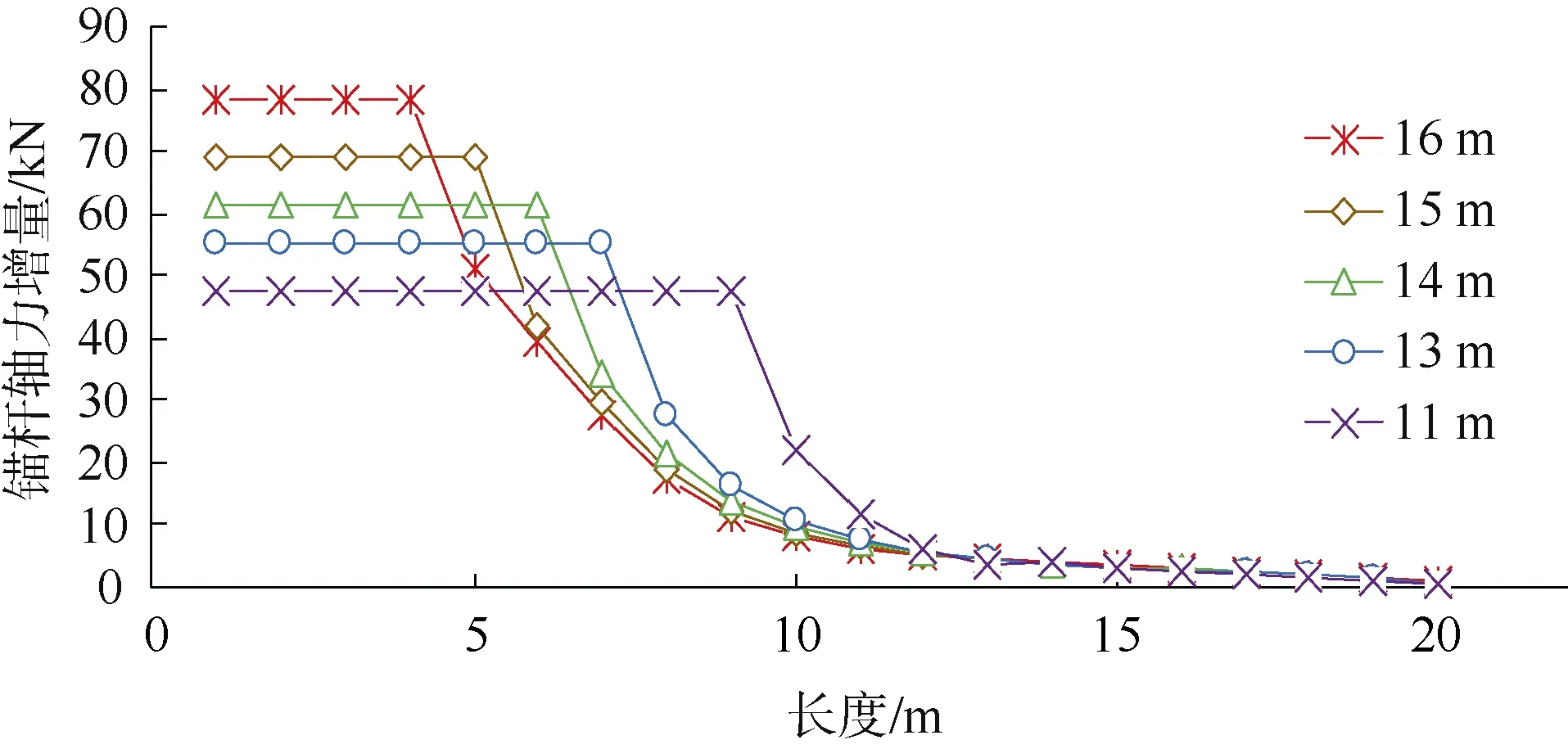
图12 不同锚固段长度下锚杆轴力增量变化曲线Fig. 12 Axial force increment under different anchor lengths

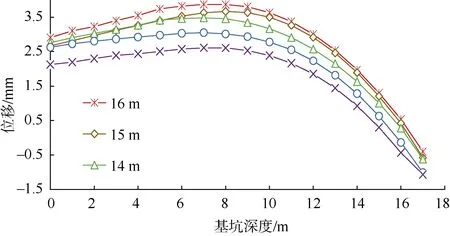
图13 不同锚固段长度下板墙水平位移变化曲线Fig. 13 Horizontal displacement under different anchor lengths

由图12、图13可以看出，随着锚固段长度的减小，各根锚杆锚头的最大轴力增量越来越小，分别为78.6、69.1、61.5、55.1和47.8 kN，其中L=11、13、14、15 m的锚头轴力增量比L=16 m时分别减少了9.5、17.1、23.5、30.8 kN，在锚杆全长不变的情况下，锚固段长度的减小有利于控制爆破作用下锚杆轴力的增大，并使其沿锚杆全长分布更加均匀合理；另一方面，板墙水平位移也随锚固段长度的减小而逐渐降低，分别为3.80、3.63、3.35、2.94和2.53 mm，其中L=11、13、14、15 m的最大位移比L=16 m时分别减少了0.17、0.45、0.86和1.27 mm。锚固段长度的降低减轻了动力作用下板墙的变形程度，有利于边坡的稳定。

4 结论

笔者研究了预应力锚板墙边坡支护结构在不同开挖位置的爆破荷载作用下的动力响应特性，得到结论如下：

1）爆破作用下锚杆轴力增量沿锚杆长度分布与静力作用下基本相同，各根轴力增量在自由段变化不大，从锚固端开始轴力增量急剧减小并都逐步趋于零。

2）通过比较板墙水平位移的数值模拟值与理论计算值得到，预应力锚板墙中板—锚结构变形协调较为一致，边坡在板—锚结构的互相作用下可使板墙部分的变形得到有效约束，大大改善了板墙的受力状态。

3）影响预应力锚板墙动力作用下受力状态和结构变形规律的因素主要包括锚杆预应力大小、爆破荷载峰值和锚杆锚固段长度等。岩质边坡预应力锚板墙支护设计和施工应综合考虑各种因素，使边坡在爆破动力作用下保持足够的稳定。