汽车建模及其动力学特性分析

吴敬东, 王 典

(沈阳化工大学 能源与动力工程学院, 辽宁 沈阳 110142)

在路面行驶的汽车经常会受到路面的激励,这些来自路面的激励都是随机的,它们经过轮胎、悬架系统作用到车身,影响乘坐人员的舒适性.同时这些随机的激励会使汽车和路面受到不同程度的载荷,从而会影响汽车的舒适性、安全性和操控稳定性.为了减小这些不利影响,需要对行驶中的汽车建立数学模型,通过数值分析计算,对汽车系统参数进行优化,以提高汽车的性能.国内外有很多学者对这些方面进行了研究.吴亮廷[1]应用matlab软件建立了汽车三维七自由度车辆振动模型,通过实验和单因素分析法对所建立的车辆振动模型的准确性及振动特性进行了模拟仿真验证.虽然线性模型和非线性模型的动力学响应在大多数情况下差别不大,线性模型能够近似反映汽车动力学性能,但是在激励幅值和激励频率比较高情况下(既汽车高速通过高度不平整路面),线性模型和非线性模型的响应相差较大[2-3].Kim C[2]等研究分析了悬架弹簧和阻尼器的物理特性,使用SPMD测试出悬架实际参数,利用曲线拟合得到悬架弹簧的非线性特性,表示为位移的三阶多项式形式,而阻尼器拟合特征是速度二阶函数.张朝杰等[4]应用多体动力学分析软件建立了铰接式自卸汽车虚拟样机模型,并进行了随机路面下的平顺性仿真研究.崔艺文等[5]研究了二自由度振动的轻型汽车模型,在用简谐激励模拟路面激励的情况下,基于Simulink进行处理和仿真,得到不同参数情况下的各位移的响应.吴颖熹[6]等通过建立十自由度车辆动力学模型,借助Matlab/Simulink对车辆振动特性进行仿真,得到增加轮胎刚度和悬挂刚度将导致汽车平顺性变差的结论.张衍成等[7]建立非平稳路面时域模型及整车振动模型,运用滤波白噪声的方法生成随机路面轮廓,借助Matlab/Simulink建立振动仿真模型,得出在非平稳路面激励下适当调整前后悬架阻尼和刚度可提高汽车乘坐舒适性的结论.文中以七自由度模型为研究对象,采用Newmark-β数值计算法研究系统参数对独立悬架幅频振动特性的影响,计算结果可为汽车结构的优化设计提供相关理论参考.

1 建立模型

考虑到汽车模型的特性,早期一些学者以单自由度和二自由度的1/4汽车模型为研究对象,后期逐渐研究四自由度1/2汽车模型.这些简单的车辆模型,不能对车辆整体的运动特征进行研究.由于路面激励方式的不同,车辆也有可能发生仰俯和侧倾运动,从而1/2模型也不能完整地模拟仿真.本文以七自由度整车模型为研究对象,其更接近实际情况.车身可以看作是一个具有侧倾、仰俯和垂直运动的刚体,前后4个车轮分别独立做垂直运动,一共7个自由度.整车振动模型如图1所示.

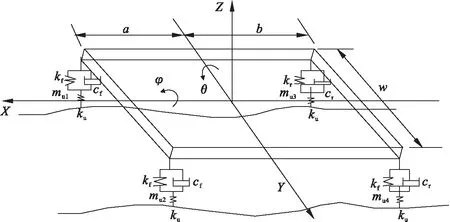
图1 具有独立悬架的7自由度整车振动模型Fig.1 With independent suspension of 7 DOF vehicle vibration model

图中车身质心处的垂直位移为z,车身的侧倾角为φ,车身的仰俯角为θ,整车簧载质量为ms,4个车轮质量分别为mu1、mu2、mu3、mu4,侧倾运动转动惯量为Ixx,仰俯运动转动惯为Iyy,前轮到质心的距离为a,后轮到质心的距离为b,整车宽度为w,前悬架的刚度系数为kf,后悬架弹簧的刚度系数为kr,前后悬架的阻尼系数为cf、cr,轮胎的刚度系数为ku.

在侧倾角和仰俯角较小的情况下,车身4个端点处的垂向位移关系为式(1)所示.

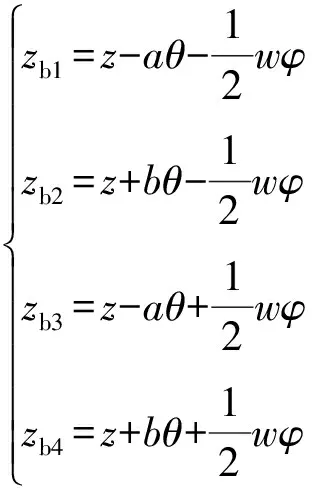
(1)

分别求出系统的动能、势能和耗散能后,由Lagrange第二类方程得出整车的振动方程如下:

车身做垂直运动方程:

(2)

车身做侧倾运动方程:

(3)

车身做俯仰运动方程:

(4)

4个车轮的垂直运动方程:

kf(zb1-zt1)

(5)

kf(zb2-zt2)

(6)

kr(zb3-zt3)

(7)

kr(zb4-zt4)

(8)

将式(1)代入振动方程(2)～(8),可以写成如式(9)所示的矩阵形式.

(9)

式中,X为位移列向量,Q为路面激励的列向量,M为总体质量矩阵,Ku为轮胎的总体刚度矩阵,K为悬架的总体刚度矩阵,C为总体阻尼矩阵,各自表达式如下:

X=[z,φ,θ,zt1,zt2,zt3,zt4]T,

Q=[0,0,0,q1,q2,q3,q4]T

2 数值仿真

振动系统中的相关参数数据[8]如表1所示.

由于研究七自由度模型,考虑到计算结果的精度,采用Newmark-β数值计算方法研究汽车悬架的振动过程.

2.1 给定参数下的仿真

按照表1给出的整车数据进行数值仿真,得到汽车振动系统的幅频特性曲线,如图2所示.

在工程实际中,汽车前后两个悬架分别具有相同的振动特性.本文为了突出研究独立悬架的动态特性,对4个独立悬架分别施加不同的外部激励,因此,得到各个悬架不同的幅频特性曲线.

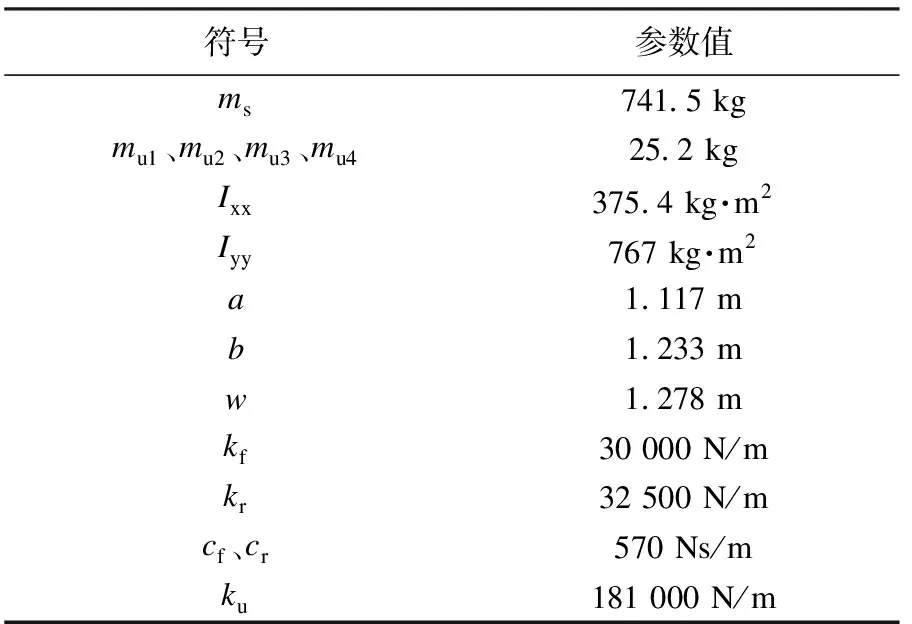
表1 振动系统的相关参数Table 1 The related parameters in the vibration system

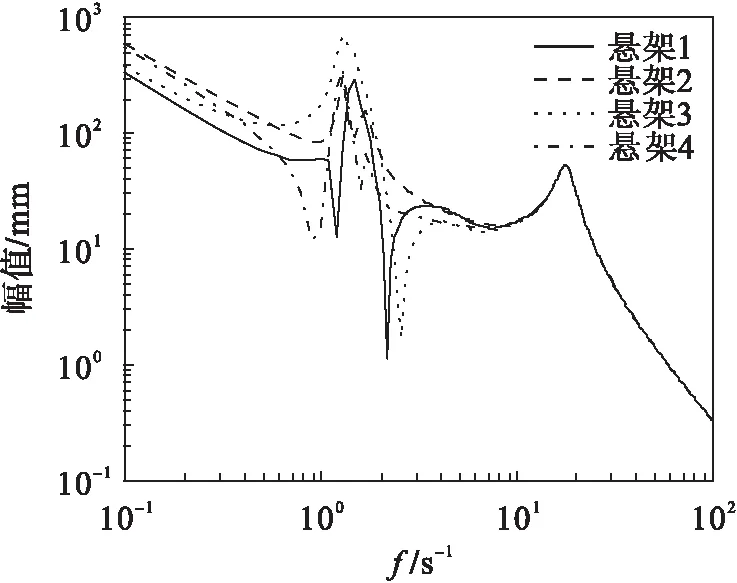
图2 系统的固有幅频特性曲线Fig.2 The inherent frequency of system characteristic Dcurve

由图2可知:悬架1在f=1.21和f=2.14处有较大的波动;而悬架2的振幅较为平缓;悬架3在f=2.63处产生波动非常剧烈;悬架4在f=1.0时出现明显的波动.因此,在对悬架进行设计时,悬架应避开f=0.8～3.0的共振区间.在f为上述一些值时,悬架的振幅波动明显,体现了汽车的幅频振动特性.

2.2 设计参数不同对结果的影响

2.2.1 悬架阻尼

采用控制变量法,对悬挂的阻尼(单位N·s/m)选取下列不同组合,(1)cf=200,cr=200;(2)cf=500,cr=500;(3)cf=1 000,cr=1 000,得到的幅频特性曲线分别如图3～图5所示.

对比图2以及图3～图5可见:随着悬架阻尼的增大,悬架1的幅值变化显著;悬架2的幅值比较稳定;悬架3的幅值变化比较大;悬架4的幅值变化不明显.结果表明:悬架阻尼的增大对悬架1、3的影响比较大,对悬架2、4的影响不大,这些影响同时也使汽车的乘坐舒适性和稳定性下降,设计悬架时应选择合理的悬架阻尼.

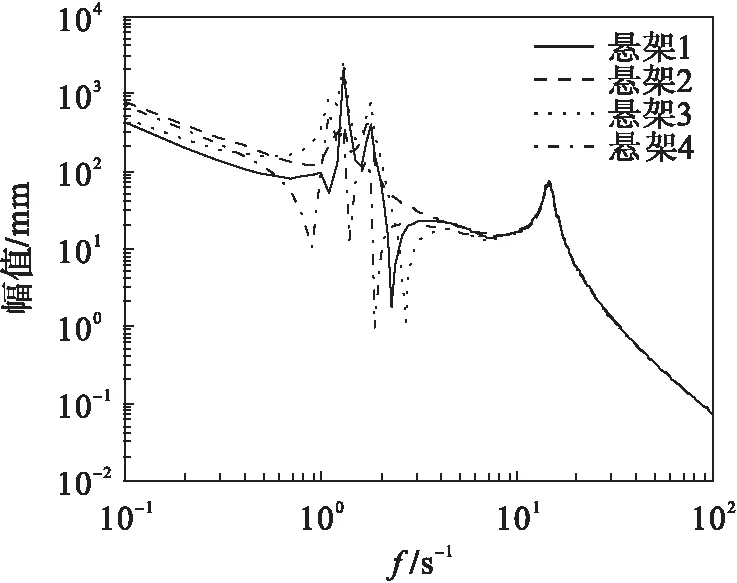
图3 cf=200、cr=200系统幅频曲线Fig.3 The amplitude-frequency curve(cf=200,cr=200)

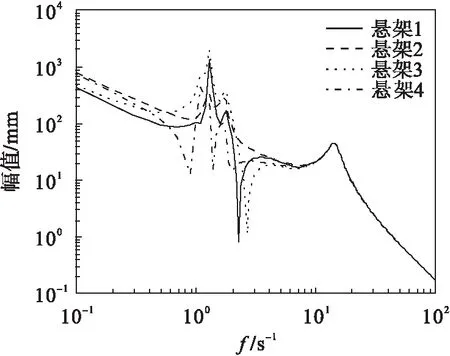
图4 cf=500、cr=500系统幅频曲线Fig.4 The amplitude-frequency curve(cf=500,cr=500)

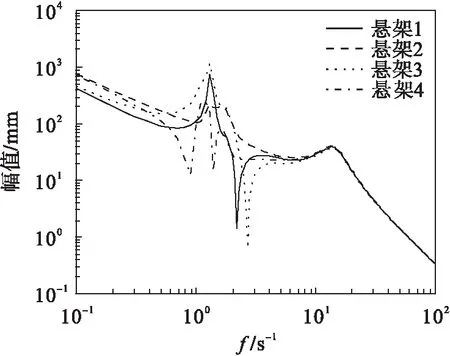
图5 cf=1 000、cr=1 000系统幅频曲线Fig.5 The amplitude-frequency curve(cf=1 000,cr=1 000)

2.2.2 悬挂刚度

采用控制变量法,悬挂的刚度(单位N/m)选择下列不同情况时,(1)kf=10 000,kr=12 500;(2)kf=20 000,kr=22 500;(3)kf=40 000,kr=42 500,系统的幅频振动特性曲线分别如图6～图8所示.

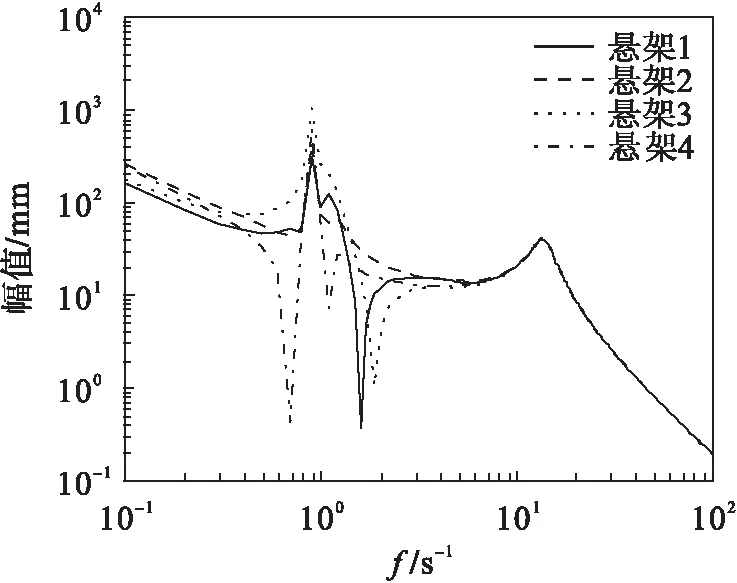
图6 kf=10 000、kr=12 500系统幅频曲线Fig.6 The amplitude-frequency curve(kf=10 000, kr=12 500)

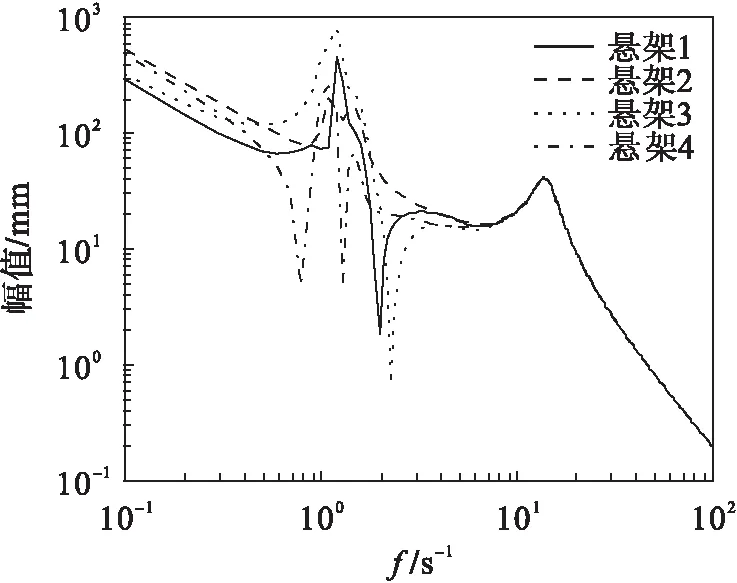
图7 kf=20 000、kr=22 500系统幅频曲线Fig.7 The amplitude-frequency curve(kf=20 000, kr=22 500)

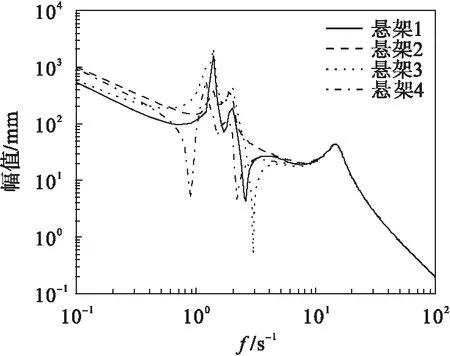
图8 kf=40 000、kr=42 500系统幅频曲线Fig.8 The amplitude-frequency curve(kf=40 000, kr=42 500)

对比图2和图6～图8,得出结论:悬架刚度的增大会引起幅频特性的很大变化,悬架1的振幅变化趋于平缓;悬架2的幅值比较稳定;悬架3的幅值变化剧烈;悬架4的振幅出现两个明显的峰值.因此,在共振区域时,随着悬架刚度的增加,汽车的操控性和安全性下降,但在频率比较高的区域,幅频特性幅值变化并不明显.

2.2.3 轮胎刚度

采用控制变量法,轮胎的刚度(单位N·s/m)分别取如下3种时,(1)ku=100 000;(2)ku=150 000;(3)ku=300 000,系统的幅频特性曲线分别如图9～图11所示.

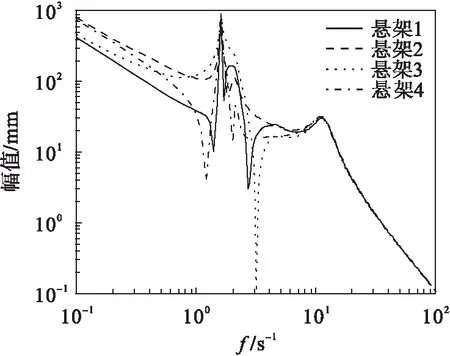
图9 ku=100 000系统幅频曲线Fig.9 The amplitude-frequency curve(ku=100 000)

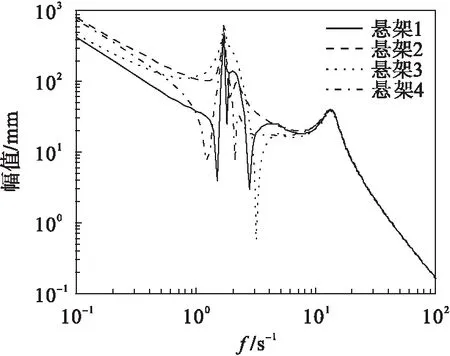
图10 ku=150 000系统幅频曲线Fig.10 The amplitude-frequency curve(ku=150 000)

对比图2以及图9～图11可以看出:随着轮胎刚度的不断增大,悬架1的振幅变化明显;悬架2的幅值变化依然比较稳定;悬架3的幅值变化非常大;悬架4的幅值变化比较大.表明轮胎刚度的增大,对悬架幅值的影响比较大,也会使汽车的乘坐舒适性和稳定性下降.

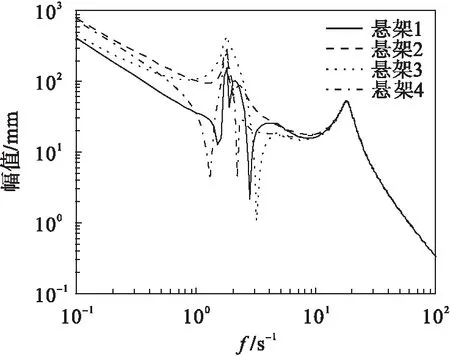
图11 ku=300 000系统幅频曲线Fig.11 The amplitude-frequency curve(ku=300 000)

3 结 论

通过分析对比以上结果,得出如下结论:系统的共振区间为f=0.8～3.0;在共振区域时,随着悬架刚度、悬架阻尼和轮胎刚度的增加,汽车的操控性和安全性下降,但在频率比较高的区域,幅频特性幅值变化并不明显;随着系统参数的变化,悬架1、3的幅值变化剧烈,悬架2、4的幅值变化不是很明显,因此,在设计悬架时应该选择合理的结构参数.