电磁能量转化与电磁场的关系研究

潘 营 利

(渭南师范学院 数理学院，陕西 渭南 714099)

在普通物理[1-2]及电磁学[3-5]教材中，人们常处理变化磁场产生电场和变化电场产生磁场的问题，以此来解释或说明一些电磁现象，但是对于电磁转换过程中的能量关系则避而不谈，这样对电磁转换过程的描述就存在着缺陷。在处理电路问题时，更多的是从电路角度讨论其能量转化关系，并没有从电磁场角度对能量的转化关系做说明，基于此，本文将从电磁场理论出发对磁产生电和电产生磁过程中的能量转化关系做了全面的说明，同时对电路中的能量转化关系也从电磁场的角度做出解释，从而使人们对“路”与“场”的关系有更深刻的理解。

1 电磁转换过程中的能量关系

1.1 磁产生电过程中的能量关系

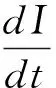
1.1.1 从坡印廷矢量的角度进行讨论

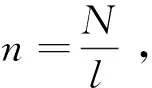
(1)

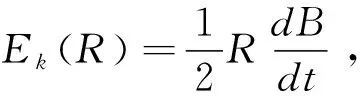
(2)

方向垂直于圆柱面指向圆柱内(如图2所示)，其大小为：

是一常数。这样单位时间内从周围电磁场进入圆柱面的能量为：

(3)

图1载流长直螺线管

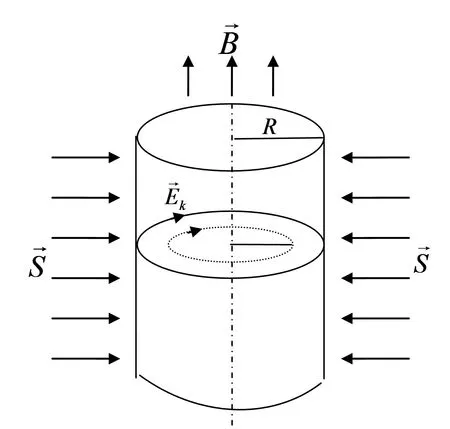
图2 变化磁场产生涡旋电场

由于磁场增大，单位时间内磁场能量的增加量为：

(4)

由(3)式和(4)式得

由此可得：单位时间内圆柱面内磁场能量的增加量来源于单位时间内从周围电磁场进入圆柱面的能量。

1.1.2 从自感电动势的角度进行讨论

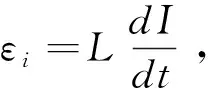
(5)

由于

L=μ0n2V=μ0n2πR2l，μ0nI=B，

代入(5)式并整理得

(6)

由此又可得：单位时间内圆柱面内磁场能量的增加量来源于单位时间内电源反抗自感电动势所做的功。

1.1.3 从涡旋电场的角度进行讨论

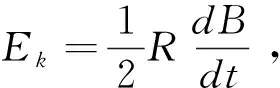
(7)

考虑到I=n0S0qv，B=μ0nI，代入(7)式得：

(8)

由此还可得出：单位时间内圆柱面内磁场能量的增加量来源于单位时间内电源反抗涡旋电场对电荷的作用力而对所有电荷所做的功。

1.2 电产生磁过程中的能量关系

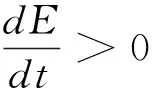
(9)

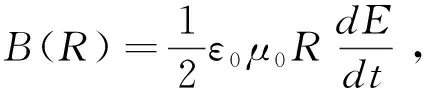
此时的坡印廷矢量大小为：

(10)

方向如图3所示。这样单位时间内电容器从周围电磁场中吸收的能量为：

(11)

单位时间内电容器中电场能量的增加量为：

(12)

由(11)式和(12)式可得：

由此可得：单位时间内电容器中电场能量的增加量来源于电容器单位时间内从周围电磁场中吸收的能量。

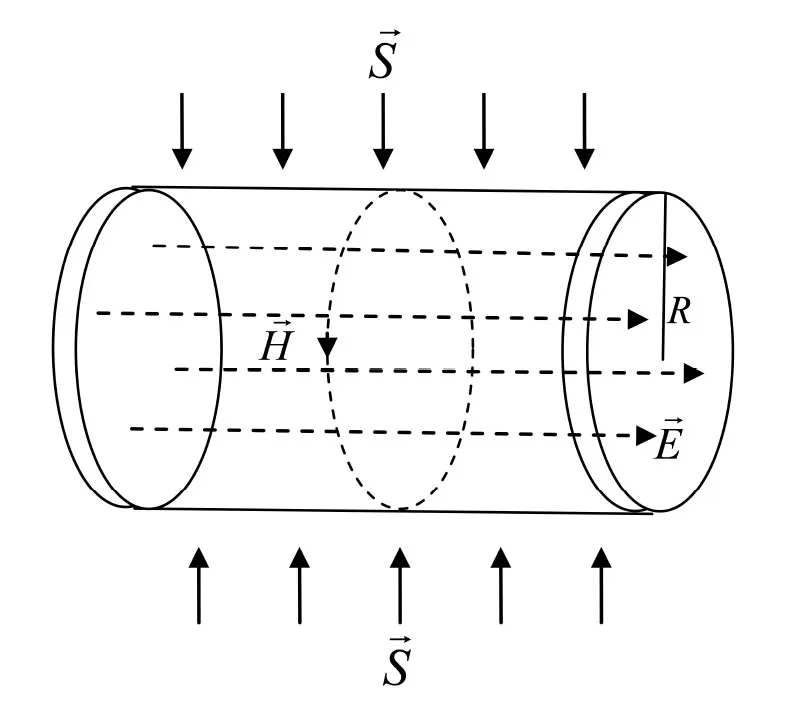
图3变化电场产生磁场

2 电路中的能量转化与电磁场

对电磁现象的研究从一开始就分为2种不同的方法，这就是“路”与“场”。“路”的理论以欧姆定律、焦耳定律为基础，以基尔霍夫定律为核心；“场”的理论以库仑定律、毕奥—萨伐尔定律、法拉第电磁感应定律为基础，以麦克斯韦方程组为核心。“路”与“场”的理论在研究多样性的电磁现象中从不同角度解释了其规律性，二者的殊途同归反映了电磁现象内在规律的和谐性。

下面从“场”的理论出发推导“路”的定律以探求“路”的定律与“场”的内在联系。

2.1 焦耳定律与电磁场

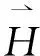
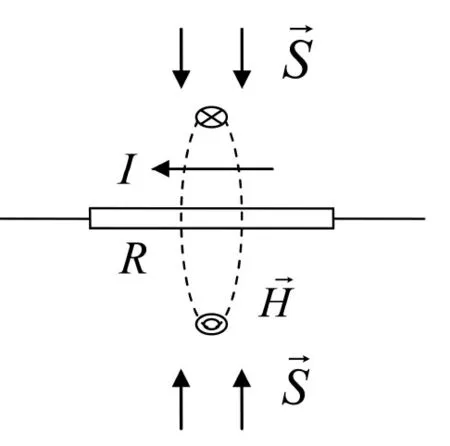
图4电阻消耗的能量与电磁场的关系

下面计算由周围电磁场向电阻传输的能量。

为研究问题方便，假定电阻截面是半径为r′的圆形，电阻的长度为l′，则有[5]:

电阻在单位时间内吸收的电磁能为：

电阻在时间t内吸收的能量全部转化为热能，即

Q=W=I2Rt。

(13)

此式即为“路”的焦耳定律。

2.2 欧姆定律与电磁场

如图5电路所示，电源的电动势为ε，内阻为R0，外电路负载电阻为R，导线电阻忽略不计。

图5简单电路与欧姆定律

由坡印廷矢量定义式知：

首先讨论几个有关矢量的方向问题：

(3)由右手螺旋定则可知，磁场方向为由电源负极向正极看去时的顺时针方向。

这几个矢量的方向如图6所示。

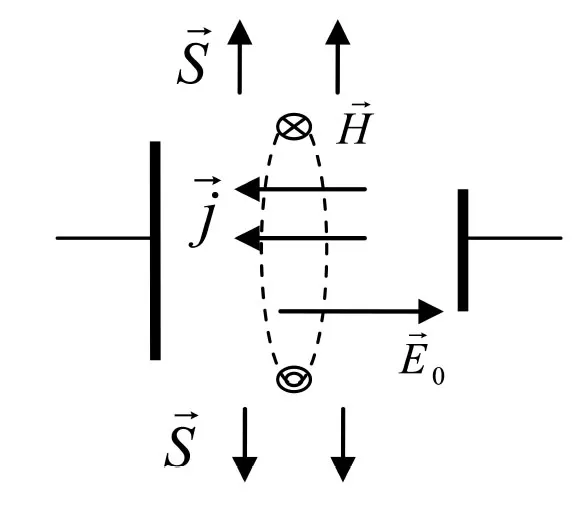
图6电源内多个物理量的方向

注意到上述各矢量间的方向关系，由

为了研究问题方便，将电源看成是截面半径为r的圆且正、负极间的距离为l，此时有

(14)

电源单位时间内向外传输的电能即电源的输出功率为

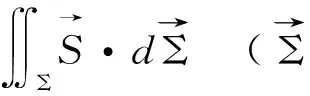
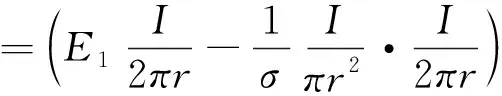
=εI-R0I2。

即

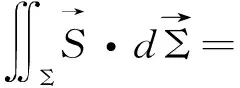
(15)

(15)式结果表示电源的输出功率等于电源的非静电功率减去电源内阻消耗的功率。由我们所研究的电路知电源的输出功率即为电路中负载电阻吸收的功率RI2，由此得出：

RI2=εI-R0I2，

(16)

(16)式即为“路”的欧姆定律。

2.3 基尔霍夫定律与电磁场

图7为电路中某一节点，作闭合曲面Σ，Σ与通过节点的导线相交被截得的面积分别为Σ1、Σ2、Σ3、Σ4。

图7节点电流之间的关系

设各导线中流过的稳恒电流分别为I1、I2、I3、I4，由电荷守恒定律知：

如果穿过节点的电流有i个，则有

(17)

此式为基尔霍夫定律的电流定律。

3 结论

(1)单位时间内磁场能量的增加量来源于单位时间内从周围电磁场中吸收的能量。

(2)单位时间内磁场能量的增加量来源于单位时间内电源反抗自感电动势所做的功。

(3)单位时间内磁场能量的增加量来源于单位时间内电源反抗涡旋电场对电荷的作用力而对所有电荷所做的功。

(4)单位时间内电容器中电场能量的增加量来源于电容器单位时间内从周围电磁场中吸收的能量。

(5)“路”与“场”的理论在研究多样性的电磁现象中从不同角度解释了其规律性，二者的殊途同归反映了电磁现象内在规律的和谐性。