最大速度在哪里
郑 琦
(浙江省萧山中学 浙江 杭州 311201)
1 原题展示
教学时经常会遇到这样一道题.
【题1】如图1所示,固定的光滑竖直圆轨道半径为R,圆心为O,AB为竖直方向上的直径.一个可视为质点的质量为m的小球紧贴圆轨道内壁做圆周运动,过A点时速度为v0,试求最大压力的位置和它的大小.

图1 题1附图
解析:由机械能守恒可知A点即为最大速度处,而最大压力也必然在A点.具体证明如下.
如图2所示,假设某时刻小球运动到C点,C处位置用角度θ表示,C处速度记为vC.
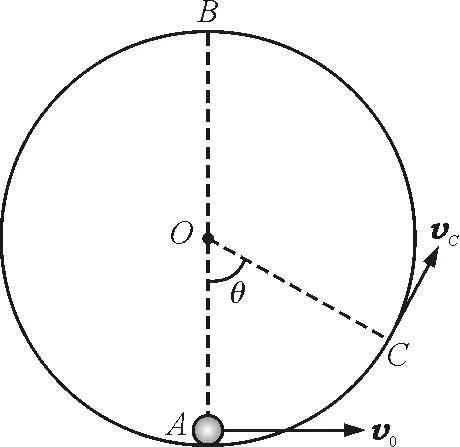
图2 题1解析用图
由机械能守恒定律和C处向心力公式,可列出以下关系
联立以上两式,可得
说明:(1)θ可取范围为[0,π],cosθ单调递减,N也单调递减.
可知A处压力最大,为
B处压力最小,为
(2)要完成完整圆周运动的条件就是能保证通过B点,即在B点处要求不脱离轨道,即
得
(3)A,B两点的压力大小之差恒为定值
NA-NB=6mg
2 思考与拓展
上题中的圆轨道是光滑的,那么如果它是粗糙的呢?最大速度还会在A点吗?压力最大也在A点吗?如果不是,它们分别在哪里?并且两个最大值的位置会在同一位置吗?
【题2】固定的粗糙竖直半圆面,半径为R,圆心为O,PQ为水平直径.从P点静止释放一个质量为m并可视为质点的小球,它与轨道之间的动摩擦因数恒为μ,试求:
(1)最大速度的位置和大小;
(2)最大压力的位置和大小.
(两个位置可用角量θ表示)
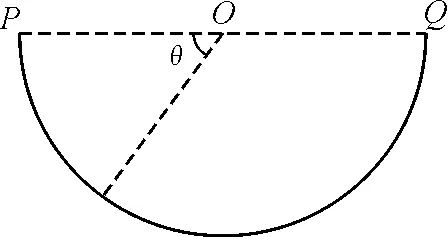
图3 题2附图
分析:速度的大小变化由切向加速度决定,如图4所示,设轨道最低点为M,对小球在轨道上任意位置时,写出切向和法向的动力学方程.

图4 题2解析用图
切向:
maτ=mgcosθ-μN
(1)
法向:
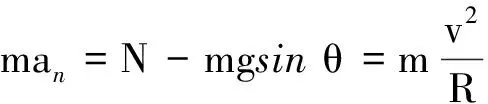
(2)
(1)定性判断

(2)半定量证明两者不在同一位置及先后关系
把式(1)、(2)用角量表示
(3)

mgcosθ1=μN(θ1)
故
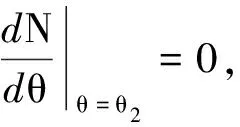
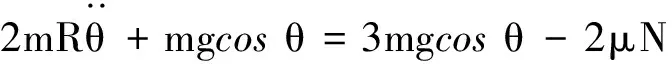
所以当θ=θ1时
而θ=θ2时
故
(4)
即A点和B点是不重合的.小球先到达速度最大处,然后再到达压力最大处.
(3)定量计算它们的位置和大小
由式(3)得到
考虑到
方程两边同乘dθ,得
移项
即
这是一个关于f(θ)的一阶线性微分方程,两边同乘e2μθ,有
e2μθf′(θ)+2μe2μθf(θ)=
即
左右同时积分并注意到等式右边部分应用分部积分方法,得到
考虑初始条件:θ=0时f(θ)=0,得
即
(5)

(6)
速度最大时,要求
即
(7)
压力最大时,要求
即
(8)
说明:
(1)式(7)、(8)为超越方程,没有解析解,只能用数值模拟逼近,可参考文献[1],笔者用计算格代数值模拟得到图5.
(2)比较式(7)、(8)可知式(7)成立时的θ1确实比式(8)成立时的θ2略小,与式(3)和图5都吻合.
数值模拟各参数如下:
v0=4 m/s,θ0=0,g=10 g/s2,m=1 kg,R=1 m,μ=0.1.
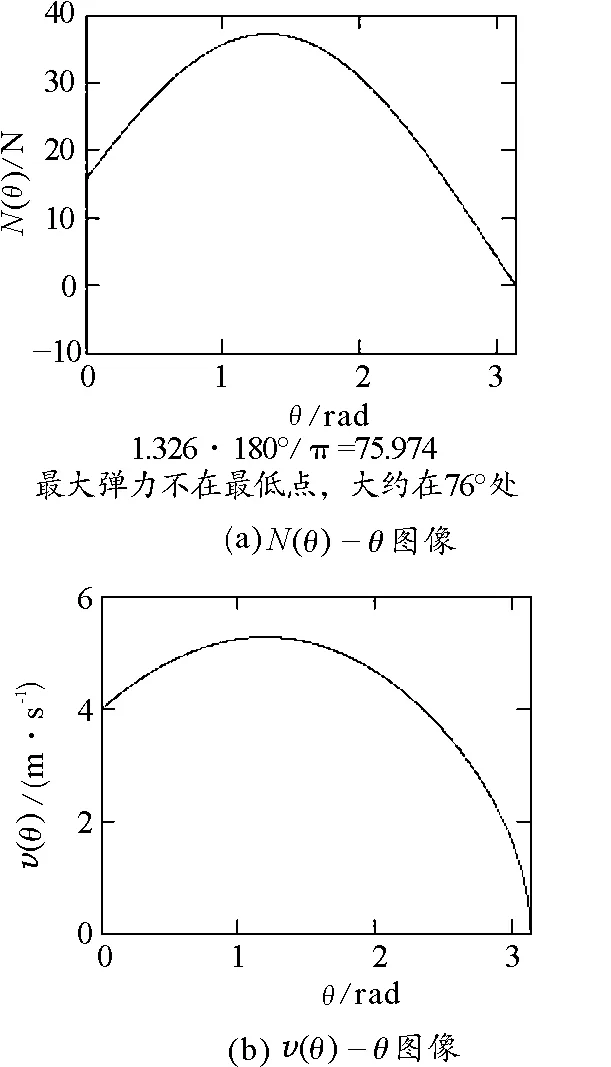
图5 数值模拟图
3 结束语
高中物理中的许多问题,如果细细追究会有很多这样类似的问题存在,对于这些问题的深度挖掘和拓展,既能提高物理教师的专业水平,又能提高命题水平和试题辨析能力,使试题更加科学,也能更好地帮助学生少走许多弯路.

