低质量流速光管内超超临界水传热特性的实验与数值模拟

曲默丰, 梁梓宇, 赵云杰, 万李, 杨冬

(西安交通大学动力工程多相流国家重点实验室, 710049, 西安)

超超临界发电机组具有大容量、高参数、低能耗等诸多特点[1]。近年来,超超临界循环流化床(CFB)锅炉和超临界水冷堆(SCWR)得到了广泛重视,国内外学者也展开了大量的基础研究[2]。管内的超临界压力水传热特性的研究是研发超超临界CFB锅炉和SCWR的基础[3]。

由于水在临界点附近物理性质发生剧烈变化,使得超超临界水具有特殊的传热特性,表现为传热强化和传热恶化两个方面。一般对超超临界水在管内流动传热时发生传热强化和传热恶化的定义为:当超超临界水的换热系数在某一焓值下出现峰值,其量级与亚临界水发生核态沸腾相当时,称为传热强化;当局部换热系数明显降低,从而导致壁温飞升时,称为传热恶化。传热强化会导致换热系数增大,此时被加热的管壁可以被充分冷却,十分有益于超临界水冷堆和超临界循环流化床锅炉的正常运行。传热恶化会引起壁温飞升从而威胁到机组的安全运行,因此二者越来越受到学者们的重视。Ackerman认为超临界下一种类似于膜态沸腾的拟膜态沸腾现象导致了传热恶化的发生[4]。Jackson等认为浮升力和热加速效应是造成传热恶化的主要原因[5]。Shiralkar的研究显示,热加速效应可能是导致这种类型传热恶化发生的主要原因[6]。由此可见,在超超临界压力下,水物性的变化、浮升力以及热加速效应对传热的影响很大,因此对这些无量纲参数展开研究是十分必要的。

对超临界流体传热的分析除了进行实验分析以外,还可以对其进行数值模拟研究。早期的研究常常使用相对简单的混合长度模型以及更为精确的k-ε模型来预测传热情况,然而模拟的结果显示,采用k-ε模型预测超临界流体传热在有些情况下与实验数据不相符。Kim等建议采用k-ε-ν2-f模型,但是该模型不能很好地预测传热恶化后下游区域温度的恢复情况[7]。文献[8-10]尝试采用SSTk-ω模型对超临界流体传热进行预测,发现该模型预测由浮升力或热加速效应引起的传热恶化效果很好。因此,本文采用SSTk-ω模型对超超临界水管内传热进行了数值模拟分析。

本文主要针对大直径低质量流速垂直管内超超临界水的传热进行实验和数值模拟分析,并用实验结果分析了各种无量纲参数对传热的影响,数值模拟结果揭示了传热强化和传热恶化的机理。

1 实验系统和方法

1.1 实验系统简介

实验系统如图1所示。实验系统中水箱内的去离子水由最大操作压力为40 MPa的柱塞泵加压,泵送出的工质水大部分进入实验回路,很少部分通过旁路回流到水箱中,用来调节实验时所需的压力和流量。流入实验回路中的工质水依次经过质量流量计和回热换热器后,在预热段中被加热,而后进入垂直实验管段被继续加热至实验工况下所需温度,同时, 实验管段的温度和压力等参数会被测量并保存,最后经过冷凝器冷却后回到水箱进行下一循环。此外,整个实验系统中加热管段均采用电加热方式。

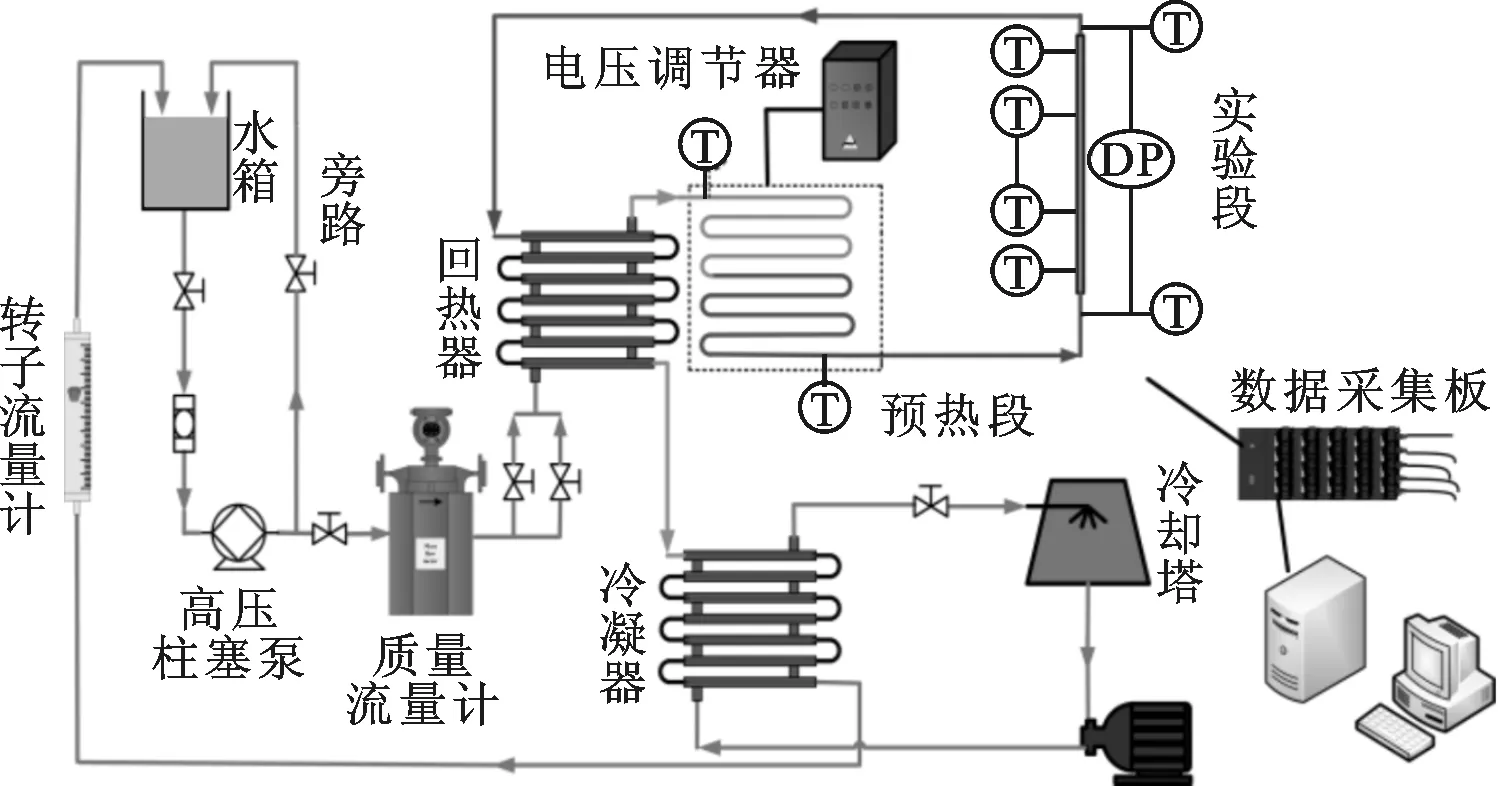
图1 流动传热特性实验系统示意图

垂直上升实验管段测量原理图如图2所示。该管段为直径30 mm、壁厚5.5 mm、长度2 m的12CrMoVG材质光管。实验管段外壁包裹绝热材料以减少散热损失;管段外壁温度由热电偶进行测量,热电偶焊接在管段外壁,其布置方式如图2中所示;管段内工质水温度由铠装热电偶测得;管段进出口压力和压降分别由压力和差压传感器测量;热流密度通过输入的电功率和热损失计算得到。

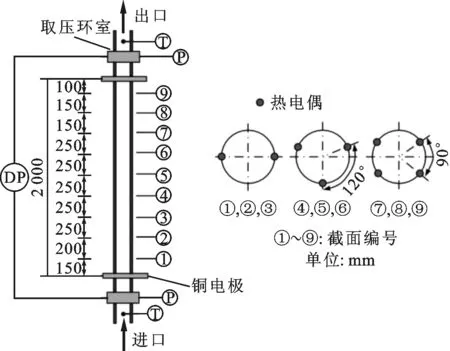
图2 实验段的结构及测点布置

1.2 实验步骤

本次实验操作的压力范围为21～32 MPa,质量流速范围为410～760 kg·m-2·s-1,热流密度范围为150～430 kW·m-2。在每个实验工况下,加在实验段上的电功率恒定以满足该工况下所需的热流密度;实验压力和质量流速也通过高压阀调节到该工况要求值;通过操作控制电柜来逐渐增加实验管段电流以提升进口工质水总焓值,直到管壁温度飞升或实验管段入口发生蒸汽过热时停止实验。

2 无量纲参数对超超临界水传热的影响分析

针对超临界压力区流体物性的特殊性,通过分析其传热机理,采用比热容比、浮升力以及热加速参数等可以较好地表征超临界流体的传热。下面就这些无量纲参数对超超临界水管内传热的影响进行讨论。

由于超超临界水在大比热容区物性剧烈变化会对传热造成很大影响,因此一般认为比热容比可以较好地反映其影响的特点。

比热容比定义为

(1)

式中:Cp,b为工质的比定压热容;Cp,a为平均比定压热容

(2)

其中hw为按内壁面温度计算的工质焓值,hb为按工质平均温度计算的工质焓值,tw为内壁温度,tb为工质平均温度。

在最近的研究中,Cheng等提出了浮升力和热加速效应对超超临界水管内传热的重要影响,这两个参数定义如下[11]

(3)

式中:πA为Cheng的热加速参数;β为热膨胀系数;q为管段热流密度;G为管段质量流速。

(4)

式中:πB为Cheng的浮升力参数;λ为工质的导热系数。

此外,Jackson提出另一种浮升力参数的表达形式[12]

(5)

式中:Bo为Jackson的浮升力参数;Re为雷诺数;Pr为普朗特数;Gr为格拉晓夫数

(6)

其中ν为工质的运动黏度。

McEligot等提出了另一种热加速参数的表达形式[13]

(7)

式中:KV为McEligot的热加速参数;μ为工质的动力黏度。

2.1 比热容比的影响

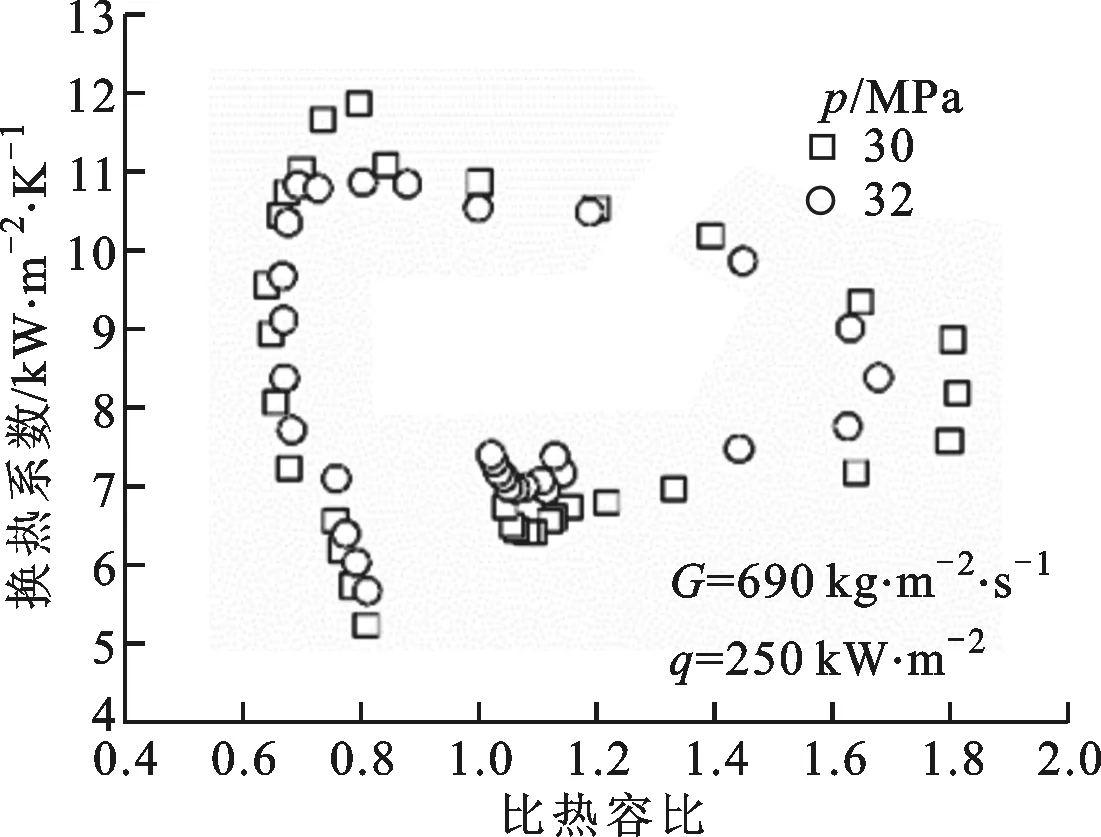
(a)不同压力

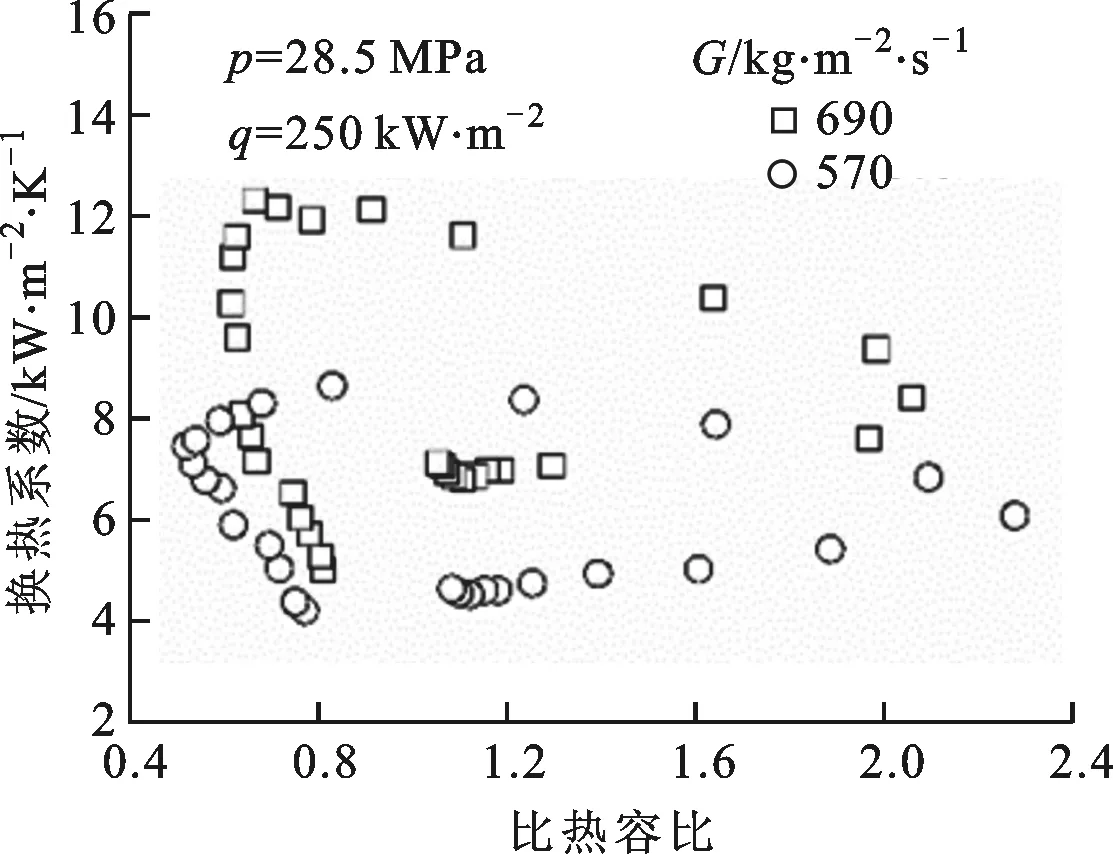
(b)不同质量流速

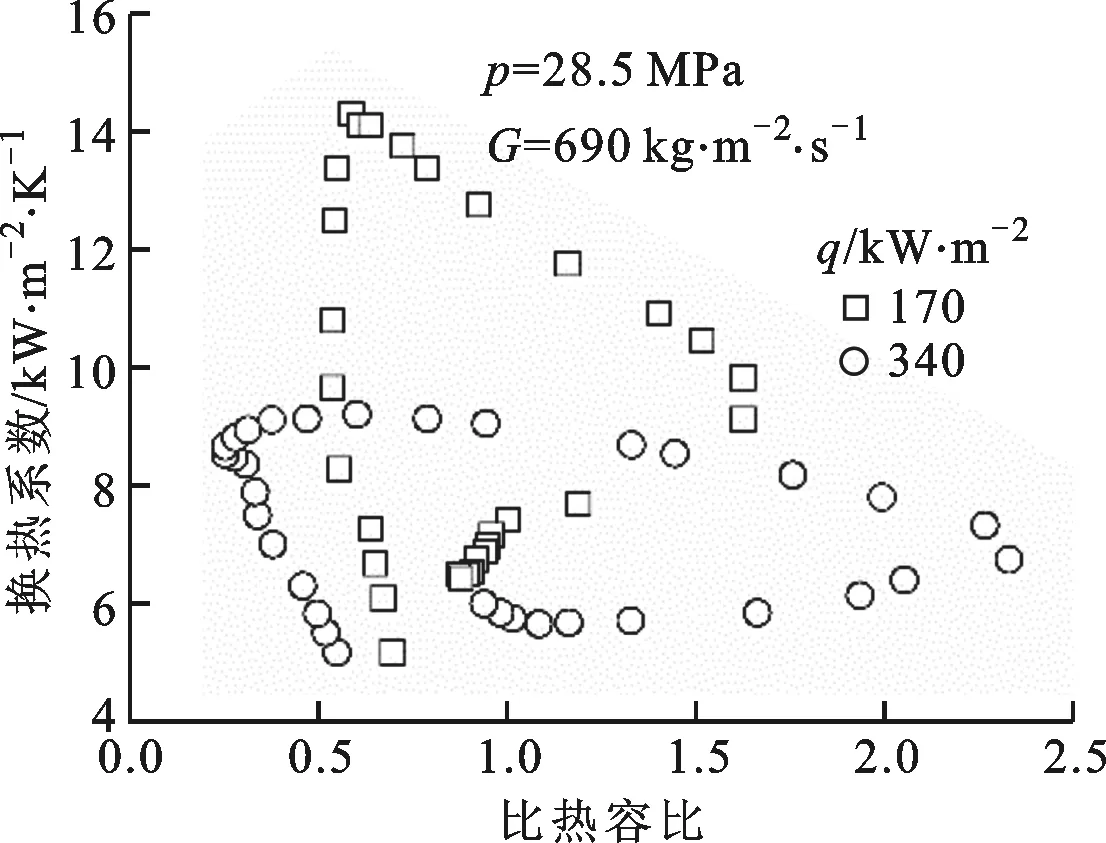
(c)不同热流密度图3 换热系数随比热容比的变化规律

为了研究比热容比对超超临界水管内传热的影响,图3给出了不同条件下换热系数随比热容比的变化情况。可以看出,换热系数与比热容比不是单值性关系,同一比热容比对应不同的换热系数,因此,利用比热容比来预测超超临界水管内传热需要补充其他参数来提高准确度。在各个工况下,换热系数峰值均出现在比热容比小于1的位置,当降低热流密度、增大压力和质量流速时,换热系数峰值向比热容比增大的方向移动,逐渐接近比热容比为1的位置。这表明比热容比小于1时发生传热强化,此时工质温度低于拟临界温度而管段内壁面温度高于拟临界温度。Ackerman指出,当拟临界温度介于工质温度和管段内壁温度之间时,会出现异常传热现象[4]。本文的研究证实,这种异常传热表现为传热强化。

2.2 热加速效应的影响

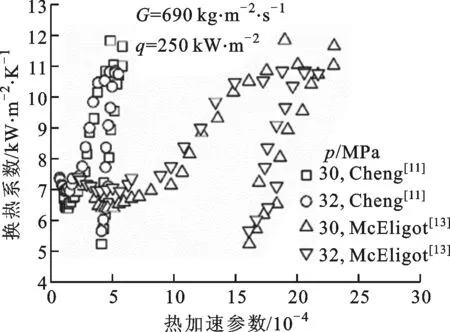
(a)不同压力

(b)不同质量流速

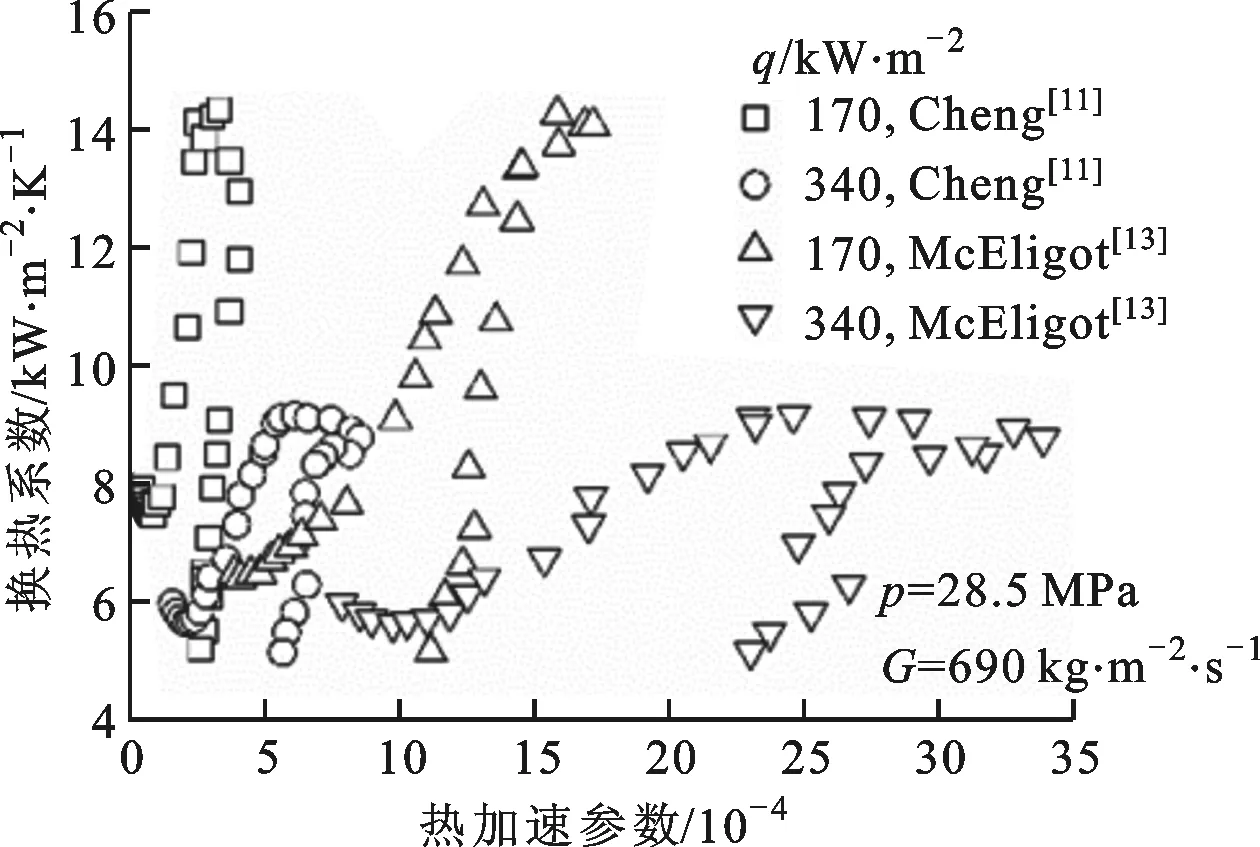
(c)不同热流密度图4 换热系数随热加速参数的变化规律

为了研究热加速效应对超超临界水管内传热的影响,图4给出了Cheng和McEligot的热加速参数对换热系数的影响。对于Cheng等提出的πA,在低焓值区,即πA较小的区域,换热系数与其呈现单值性关系,二者一一对应;进入大比热容区后,πA逐渐增大并与换热系数一同达到峰值,此时β/Cp,b最大,可看出,虽然Cp,b增大,但是β的增幅以更大,使得πA在拟临界温度处达到最大值;随后πA随焓值的增大而减小,从而出现同一πA对应多个换热系数的现象。可见,πA对应的热加速效应在拟临界温度前逐步增强,在拟临界温度处影响最大,而后影响逐渐减弱。同样地,McEligot等提出的KV也表现出相同的规律,不再赘述。因此,这不能说明热加速效应对传热的影响占据主要地位,无论是采用上述哪种形式的热加速参数来预测超超临界水管内传热,都需要补充相关参数以提高预测准确性。

2.3 浮升力的影响

(a)不同压力

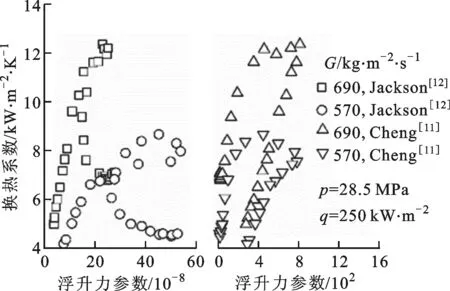
(b)不同质量流速

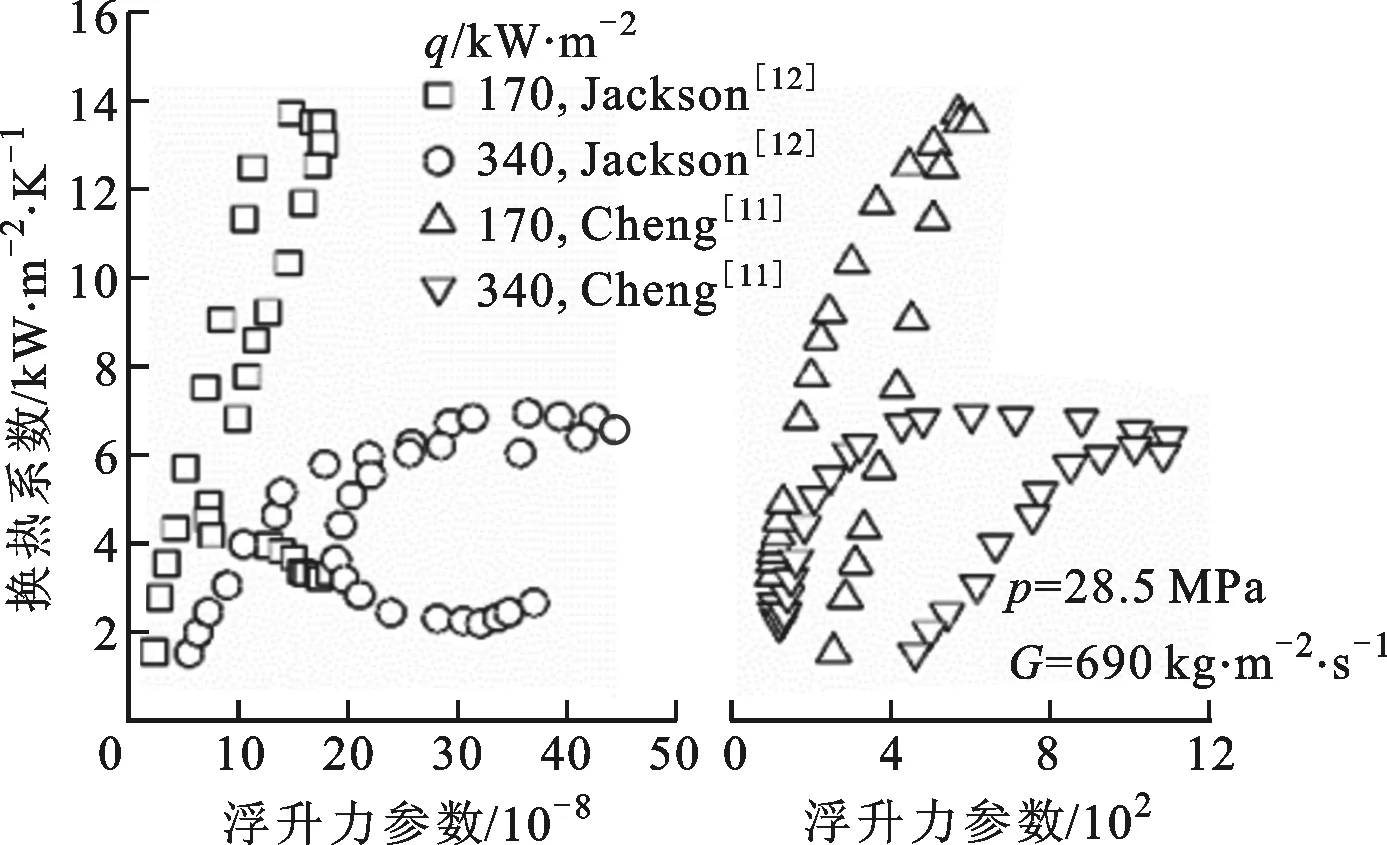
(c)不同热流密度图5 换热系数随浮升力参数的变化规律

为了研究浮升力对超超临界水管内传热的影响,图5给出了Cheng和Jackson的浮升力参数对换热系数的影响。对于Cheng等提出的πB,其对传热的影响为先增强后减弱,并且压力越小、热流密度越大,影响更加明显,但是对质量流速的变化不敏感。同样,Jackson提出的Bo对传热的影响也是先增强后减弱,与πB不同的是,Bo对压力不敏感,随着质量流速的减小和热流密度的增大而增大。热流密度的改变会导致工质密度差发生变化,是造成浮升力变化的主要因素,从图5来看,πB和Bo都对热流密度表现出较强的敏感性。由于在浮升力较大的区域,πB或Bo与换热系数之间都不存在较强的单值性关系,因此上述浮升力参数均不能完整地预测超超临界水管内传热,需补充相关参数。

3 数值模拟与验证

数值模拟部分选择与实验管段相同的管长2 m、管径30 mm、壁厚5.5 mm的光管模型进行模拟分析。整个管段均匀加热,为了保证数值计算的连续性,管段入口处的流体流速和湍流强度大小由前一次模拟结果决定,管段出口设置为压力出口,内壁表面设置为无滑移边界条件。

图6 计算网格划分示意图

管段的结构化网格由ICEM软件生成。由于边界层对传热影响很大,因此该区域的网格需要加密处理,如图6所示。为了验证网格独立性,本文分别对网格数为1.5×106、2.8×106、4.6×106、7.2×106的模型进行了计算。由模拟结果可知,当网格数达到4.6×106后,计算结果基本不发生变化,因此本文模拟部分网格数为4.6×106。

对管段中流体的超临界传热模拟采用ANYSYS FLUENT软件,计算时用FLUENT调用NIST REFPROP软件将工质物性设置为定压条件下随温度变化的函数。计算过程中监视残差以及出口的温度、速度、流量、湍动能和内壁面平均温度等参数的变化,当这些被监视参数的相对变化率小于10-6时判定收敛。

为了验证模型的准确性,选取本文光管实验结果和Ackerman光管实验结果[4]对模型进行验证,结果如图7所示。图7a表明SSTk-ω模型的预测结果与实验数据吻合很好,说明该模型能够预测光管内超临水的传热强化;图7b表明SSTk-ω模型能够预测传热恶化发生时管壁温度飞升的位置以及恶化后传热的恢复情况,但是预测的峰值有一定偏差。可见,SSTk-ω模型能够较为准确地预测光管内超超临界水的传热情况。

(a)与本文实验结果的比较

(b)与Ackerman实验结果的比较图7 数值模拟模型验证结果

4 超超临界水传热强化及传热恶化数值模拟结果与分析

4.1 传热强化

本文选取p=30 MPa、G=690 kg·m-2·s-1、q=250 kW·m-2的工况进行数值模拟以及传热强化机理分析,如图8a所示,选取传热强化过程中换热系数从低到峰值所对应的A、B和C截面,不同流体温度下流场的详细信息分别表示在图8中。

(a)A、B、C截面位置

(b)工质温度

(c)轴向速度

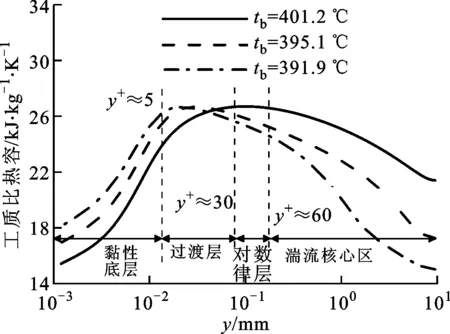
(d)工质比热容

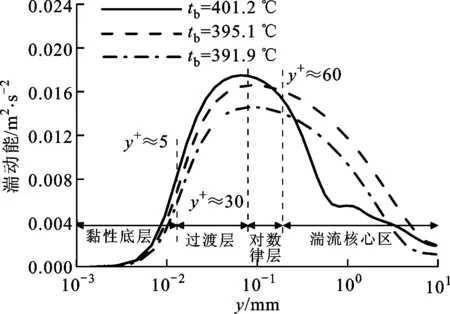
(e)湍动能图8 传热强化工况下的流场参数变化

在黏性底层,A截面的比热容最大,C截面比热容比其他两截面低;在过渡层和对数律层,A截面比热容达到最大值后开始减小,C截面比热容最高。这是因为在黏性底层,A截面处内壁附近温度接近拟临界温度,因而比热容最大。虽然C截面在黏性底层的比热容最小,但该区域狭窄,而在过渡层以及对数律层,C截面处工质比热容最大,由于这两个区域相对于黏性底层要宽得多,因此C截面处边界层内大比热容工质的份额仍然是最大的,使得C截面处换热系数最大,传热效果最好,可见边界层内大比热容工质份额是影响传热的重要因素之一。

随着换热系数的增大,在黏性底层和过渡层,从A截面到C截面的湍动能增加,但在对数律层的后段以及湍流核心区,由于湍流扩散较热扩散的影响小,使得C截面湍流强度不是最强但是传热效果最好。可见,在传热强化工况中,湍动能不是影响传热的最主要因素。

4.2 传热恶化

本文选取文献[4]中发生传热恶化的工况(p=24.8 MPa、G=404 kg·m-2·s-1、q=284 kW·m-2)进行数值模拟以及传热恶化机理分析,如图9所示,选取了图7b中恶化最严重的M截面和下游恢复后的N截面,不同流体温度下流场的详细信息分别表示在图9中。

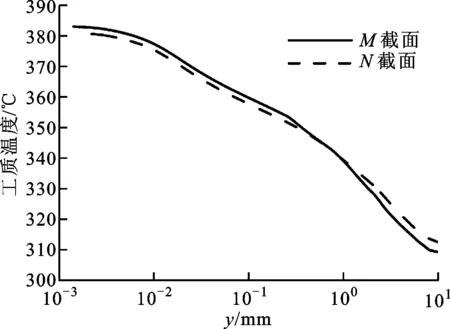
(a)工质温度

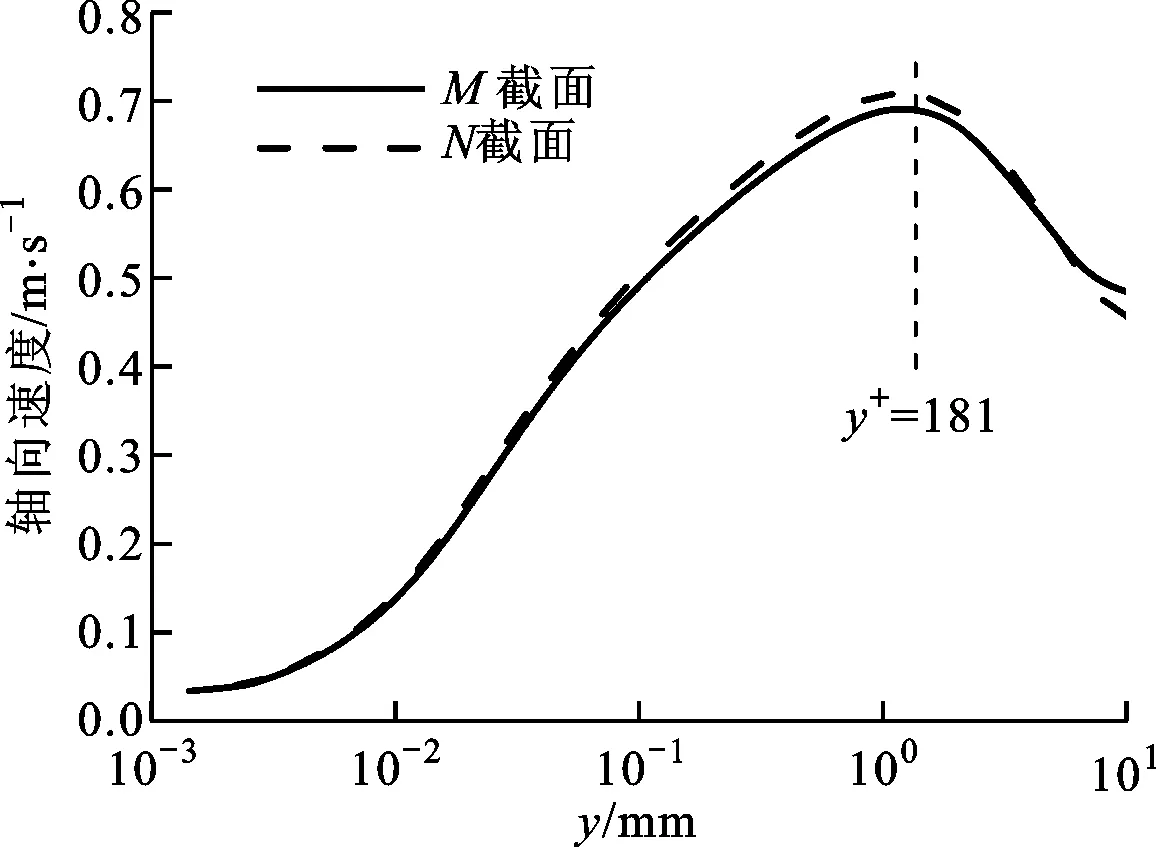
(b)轴向速度

(c)工质比热容

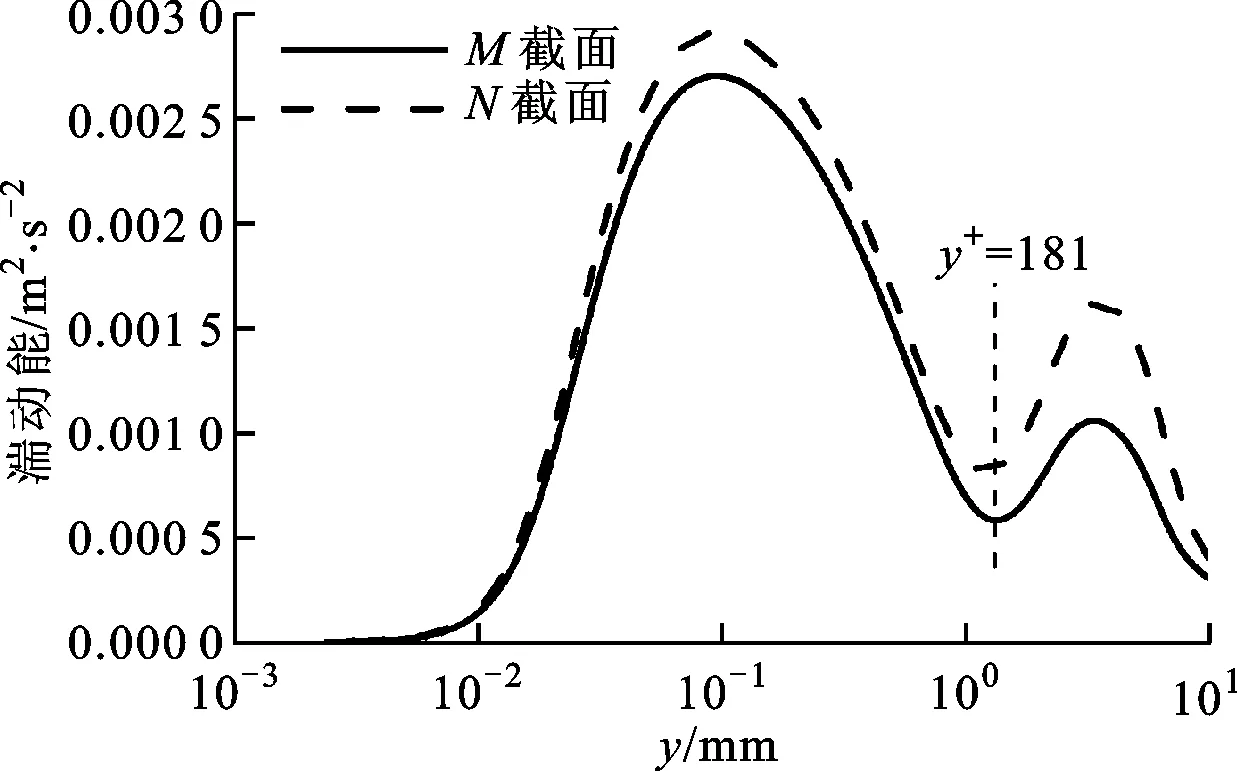
(d)湍动能图9 传热恶化工况下的流场参数变化

传热恶化工况下工质径向温度梯度大,即温度下降迅速。近壁面区域流体浮升力作用使得轴向速度显著增大。在垂直上升管内流动中,浮升力与流体流动方向相同使得轴向速度增大,其中轴向速度最大值位于y+=181处。M截面的湍动能(k)较N截面小很多,即M截面发生传热恶化,k先沿径向增大到峰值,而后在y+=181即轴向速度峰值位置减小到最小值,这表明k的径向分布与轴向速度沿径向的分布关系紧密。Li等也得到了类似的结论[14]。其主要原因为,在y+=181位置径向速度梯度降低到最小值,剪切应力的降低导致k降低,此处雷诺数很小,流动接近层流,径向的传热传质微弱,热量不能及时被流体带走从而导致M截面温度突增,即发生了传热恶化。此外,该位置流体的比热容急剧减小,流体吸热能力也随之降低,加剧了传热恶化的发生。

5 结 论

本文从实验和模拟两个方面对超超临界水管内传热进行了研究,得到的主要结论有:

(1)针对比热容比、浮升力以及热加速参数对超超临界水管内传热的影响进行了讨论,这些量纲一参数与换热系数之间都不存在很强的单值性关系,采用上述参数预测超临界流体传热时需要补充其他参数;

(2)通过与实验数据对比可知,采用SSTk-ω模型能够较为准确地模拟出超临界流体传热强化和传热恶化过程;

(3)根据模拟结果获得了超临界流体发生传热强化和传热恶化的物理机理,边界层内的大比热容工质份额和浮升力作用分别是导致传热强化和传热恶化的主要原因之一。