谐波齿轮负载侧隙和啮合力分布规律研究

陈晓霞, 杨朋朋, 邢静忠, 姚云鹏

(1.天津工业大学天津市现代机电装备技术重点实验室, 300387, 天津; 2.天津工业大学机械工程学院, 300387, 天津)

谐波齿轮传动凭借其传动比大、体积小、结构简单、重量轻、承载能力大和传动精度高等优点,被广泛应用于航天航空、工业机器人、精密机床、仪器仪表等领域[1]。随着机器人技术的迅猛发展,在未来5年,谐波减速器将在高精度、高承载能力等相关技术方面大力发展[2]。目前,指导和评价谐波齿轮齿廓设计的几何学指标为空载侧隙及影响回差的背隙[3-4],目的是为了保障传动运动的精度。对于负载工况下的谐波齿轮传动,齿间啮合力既是柔轮强度计算的基础,同时又对定位精度和动态稳定性等啮合性能有重要影响。

随着计算技术的发展,很多研究者通过建立等厚度壳体的柔轮有限元模型,计算了空载状态下柔轮的结构应力和变形[5-6]。伊万诺夫依据实验数据,给出了齿间啮合力分布的经验公式[1]。基于该啮合力分布,董惠敏将柔轮简化为没有轮齿的等厚度壳体有限元模型,在柔轮中面上施加啮合力,计算了传动状态下柔轮不同截面上的变形和应力[7],并基于动态啮合仿真给出的啮合力,提出了渐开线齿廓的优化设计方法[8]。考虑到传动荷载应该作用在轮齿上,陈晓霞等采用变截面壳单元和梁单元相结合的柔轮有限元模型,对波发生器及传动荷载共同作用下的柔轮应力以及齿根和齿尖处的变形进行了分析[9],并对不同波发生器作用下柔轮中面的伸缩变形进行了研究[10-11]。考虑到柔轮轮齿的影响,刘文芝等建立了实体单元柔轮模型,用三维弹性接触分析研究了柔轮应力和轮齿变形,计算分析了承载柔轮齿圈和筒体的应力分布规律[12]。Li利用自编有限元软件建立实体有限元模型,计算了空载和负载状态下柔轮杯底的应力,并进行了实验验证[13]。

考虑到柔轮在负载工况下的动态啮合状态,郑德林等采用边界元法计算柔轮变形,用轮齿的重叠量修正啮合力,获得了齿间啮合力分布[14]。乐可锡等考虑传动元件的弹性、间隙、误差等影响因素,提出了求解谐波齿轮空间动态啮合力的直接迭代方法[15]。崔博文等在实体有限元模型上定义了波发生器与柔轮内壁、柔轮齿与刚轮齿之间的接触关系,计算了不同负载状态下的啮合齿对数和啮合力分布[16]。姜世平等通过在刚轮上安装活齿测得的啮合力数据,利用统计方法得到啮合区切向力和径向力的实验曲线,从而获得了载荷区的内载荷分布方程[17]。上述研究从理论分析、数值模拟和实验验证等方面,对揭示谐波齿轮多齿啮合特性起到了重要的推动作用。

目前,对实际工况下的谐波齿轮多齿对啮合工作状态尚缺乏简单有效的分析计算方法,难点在于:①影响因素多,因为啮合力与齿廓形状、空载状态下的空载侧隙分布及负载大小相关;②波发生器与柔轮、柔轮齿与刚轮齿之间的接触是非线性的,使啮合力计算建模复杂,分析耗时;③齿形很小,且多齿啮合的啮合侧隙在几微米到十几微米之间,实验验证非常困难。因此,啮合状态的有限元仿真成为一种有效可行的计算方法。

为反映负载工况下谐波齿轮的啮合特性,本文提出一种基于周向啮合刚度矩阵和空载侧隙的啮合力迭代算法。利用精确算法计算装配状态下的空载侧隙;建立参数化的、输出端固定的柔轮有限元模型,定义波发生器与柔轮内壁的接触关系,利用逐一施加单位啮合力的方法,提取单位啮合力与啮合点周向位移对应关系的啮合柔度矩阵,得到能更真实反映柔轮齿廓啮合点周向刚度特性的啮合刚度矩阵;根据空载侧隙,迭代计算不同负载工况下刚轮齿廓与柔轮齿廓间的负载侧隙和啮合力;建立包含刚轮齿廓和柔轮齿廓接触关系的实体有限元模型,仿真验证不同负载工况下的负载侧隙和啮合力分布,以及扭转刚度特性。

1 利用精确算法计算空载侧隙

装配状态的柔轮变形后,轮齿的位置由波发生器的形状确定。空载侧隙是指装配变形后柔轮轮齿与刚轮轮齿间的最小间隙。装配状态下谐波齿轮的空载侧隙与齿廓形状和波发生器类型相关。本文以双圆盘波发生器作用下的渐开线齿廓杯形柔轮为例进行计算分析。

1.1 基于精确算法的变形后柔轮轮齿定位

图1所示为双圆盘波发生器作用下的柔轮中性层变形示意图,图中R为圆盘的计算半径,e为圆盘轴线的偏心距,γ为柔轮对圆盘的包角,u0为最大径向变形。

在波发生器作用下,柔轮的中性层横截面从变形前半径为rm的圆形(见图1)变为非圆曲线(图1中径矢为ρ的粗实线)。

中性层任意位置φ处的点在变形后的矢径

ρ=rm+u(φ)

(1)

式中:rm为变形前柔轮中性层曲线的半径;u(φ)为变形后柔轮中性层曲线上任意点的径向位移。

图1 双圆盘波发生器作用下的柔轮中性层变形

在双圆盘波发生器作用下,柔轮变形以包角γ为界,包角范围内柔轮齿圈变形后与波发生器完全贴合,其径向变形为u1,其余的径向变形为u2。

(2)

式中:A1=π/2-γ-sinγcosγ;B1=4[cosγ-(π/2-γ)sinγ]/π。

波发生器迫使柔轮啮合端中性层产生径向位移u(φ)、周向位移v(φ)和轮齿对称轴相对于径矢的转角θuz(φ),如图2所示。柔轮啮合端中性层与齿对称线的交点Of从初始φ位置移动到φ1位置,轮齿对称线也转至图示xf方向。

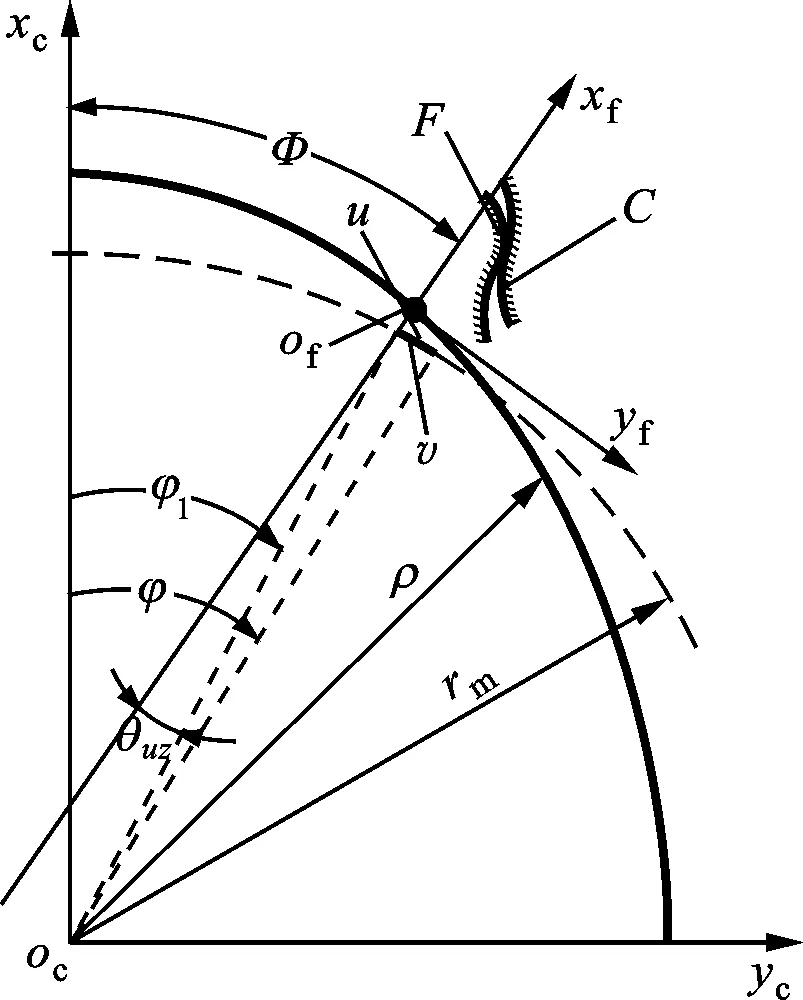
图2 柔轮啮合时的几何关系

依据中性层变形曲线不伸长条件

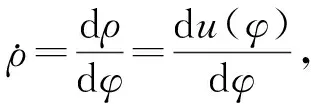
v=-(φ1-φ)rm

(3)

相对于变形后的齿根极径OcOf,轮齿对称轴xf的转角

(4)

1.2 渐开线齿廓谐波齿轮的空载侧隙

用参数s表达的渐开线右侧齿廓方程[19]为

(5)

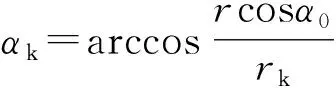
装配变形后的柔轮齿面和刚轮齿面间的最小周向距离,即该齿对间的侧隙

(6)

点K1(xK1,yK1)是利用极值求解方法沿柔轮齿高方向取点对比计算出的柔轮齿廓到刚轮齿廓的最小周向距离点,刚轮齿廓啮合点K2(xK2,yK2)为极径与K1相等的刚轮齿廓上的对应点。

1.3 基于实体有限元模型的侧隙验证

由于空载侧隙是啮合力计算的基础,为此本文建立含真实渐开线齿廓信息的柔轮和刚轮有限元模型,对装配状态的柔轮变形和侧隙结果进行验证。某电子传动设备的额定扭矩为7 N·m,其谐波齿轮的齿廓参数和结构参数如下:模数m=0.2,压力角α0=20°,柔轮最大径向变形量u0=0.2 mm,柔轮齿数z1=140,刚轮齿数z2=142;柔轮齿根圆半径rf=14.156 mm,齿顶圆半径ra=14.584 mm;柔轮变位系数x1=2.13,刚轮变位系数x2=1.925;齿圈壁厚δ1=0.3 mm;柔轮筒内半径ri=13.856 mm,筒长l=30 mm,筒体壁厚δ2=0.273 mm;柔轮齿圈的宽度b=4 mm,柔轮中性层曲线半径rm=14.006 mm,柔轮杯底固定孔内径drim=14.156 mm;圆盘轴线的偏心距e=0.6 mm。

柔轮、刚轮齿廓选用SOLID45单元。利用二分法求解渐开线齿廓从齿顶到齿根6个均布的齿廓参数s,基于齿廓方程(5)得到6个不同的关键点坐标,再用样条函数曲线连接生成柔轮、刚轮齿廓。柔轮筒体和双圆盘波发生器外表面选用SHELL63单元。双圆盘波发生器用2个对称的圆面来表示,定义波发生器外表面与柔轮内壁的接触为刚体与柔体的面-面接触单元。以波发生器的上半圆为目标面,定义Targe169目标单元;以柔轮的内壁为柔性接触面,定义Conta172接触单元。固定约束柔轮杯底圆孔和波发生器表面,求解装配状态下的柔轮变形。图3所示为谐波齿轮传动的有限元装配模型。

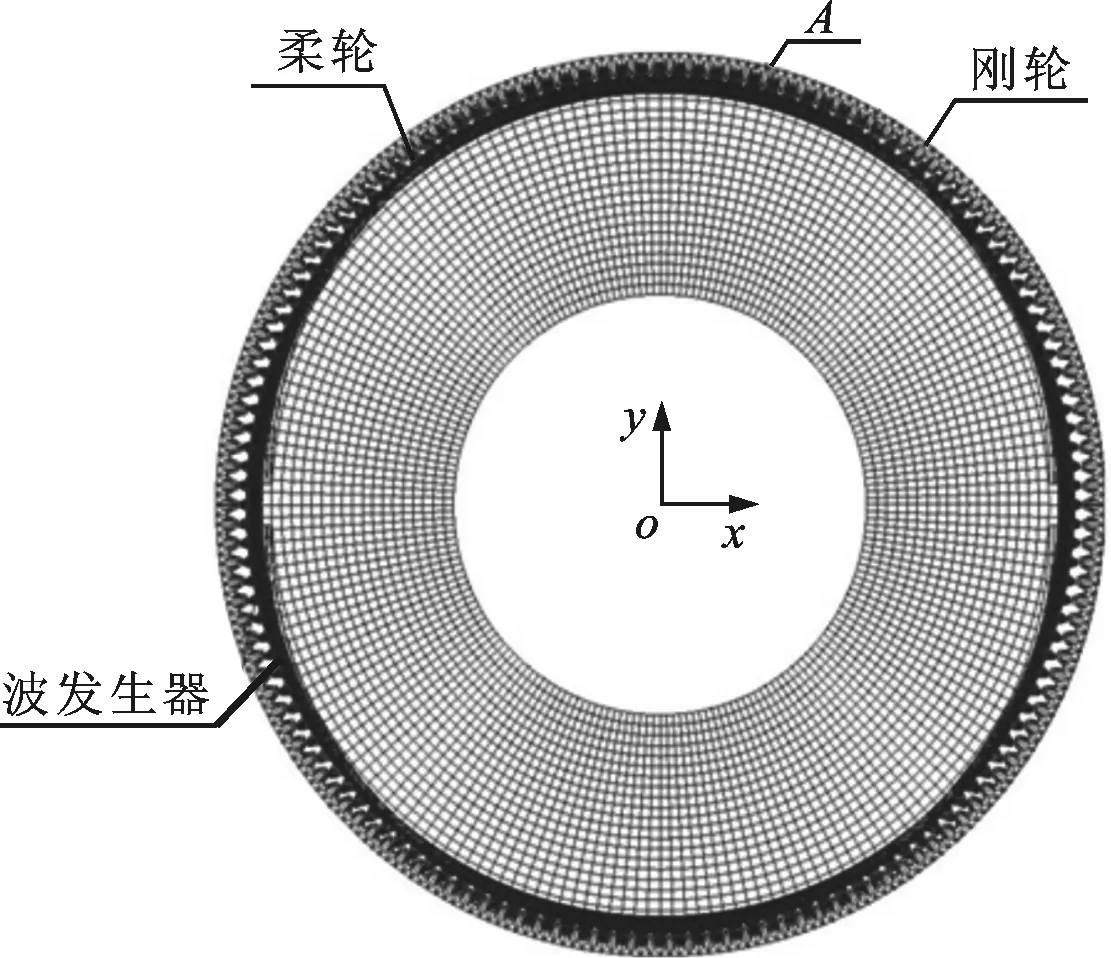
图3 谐波齿轮传动的有限元装配模型

图4为图3中柔轮齿与刚轮齿啮合的局部放大图,图中的数值为柔轮齿廓和刚轮齿廓的节点编号。

图4 柔轮齿与刚轮齿啮合的局部放大图

柔轮齿廓在柔轮变形后发生位置和形状的改变,因此,柔轮齿廓变形后的位置根据齿廓上节点变形后的位置得到。这样,柔轮齿廓和刚轮齿廓间的最小周向距离简化为变形后柔轮齿廓上的节点到刚轮齿廓的周向最小距离问题。

图5所示为空载侧隙的本文算法理论解和有限元分析结果,图中横坐标是啮合齿位置的极角,φ=0°表示长轴,顺时针为正。图5显示,2种算法的空载侧隙在φ<25°区域内基本一致,其他位置的理论解略大于有限元结果。

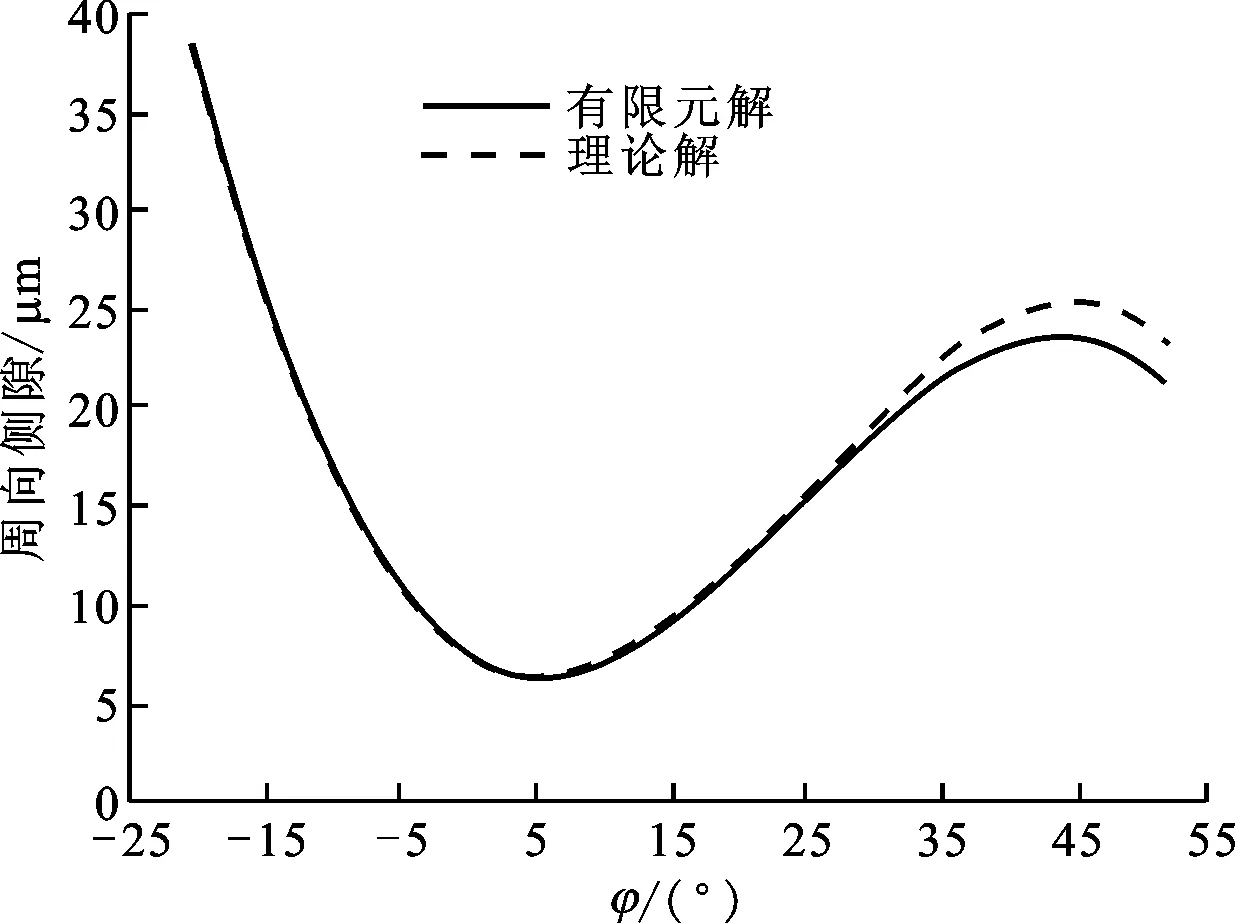
图5 本文算法与有限元模型计算的空载侧隙

1.4 侧隙偏差的影响因素分析

柔轮轮齿的刚度远大于齿圈的刚度,故通常认为柔轮在波发生器的作用下只是轮齿对称线与中性层曲线交点的位置产生径向位移u(φ)、周向位移v(φ)和相对于径矢的转角θuz(φ),轮齿本身不变形[19]。图6所示为双圆盘波发生器作用下柔轮齿圈中性层变形位移的本文算法理论解与有限元解的比较,图中横坐标0°对应长轴位置,顺时针为正。为方便比较,将本文算法式(2)、式(3)和式(4)中的径向位移、周向位移和法线转角进行归一化:Cu=u/u0;Cv=2v/u0;Cθuz=θuzrm/(2u0)。

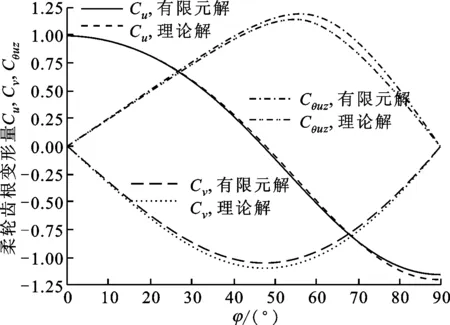
图6 柔轮中性层位移的理论解与有限元解

图6显示,在0°<φ<55°区间上,径向位移的理论解与有限元结果在啮合区间上基本一致;短轴处理论解略偏大,但不在啮合区间,不会影响侧隙;周向位移的理论解和有限元模型结果在长、短轴处完全一致,在其余位置小于有限元结果;法线转角的理论解在φ<45°处偏小,其余位置偏大。

理论解的周向位移和法线转角偏小都会引起侧隙偏大。由于齿高很小,法线转角偏差对侧隙影响不大,故柔轮中性层的周向位移偏差是空载侧隙偏差的主要来源。

2 啮合刚度矩阵及其性质

柔轮啮合刚度系数是引起柔轮啮合点单位周向位移所需的啮合力。柔轮周向位移由轮齿变形和柔轮筒体变形2部分组成,而轮齿变形又包括齿间接触变形、轮齿弯曲变形和柔轮齿圈变形。谐波齿轮柔轮受载后,柔轮筒体本身还会产生一定程度的畸变,因此理论推导啮合刚度非常复杂。本文通过三维实体单元的柔轮有限元模型进行啮合刚度矩阵的计算。

2.1 模型建立及装配变形求解

谐波齿轮传动中柔轮的变形是由波发生器和啮合力共同作用的结果,因此求解装配状态下的柔轮变形是求解负载状态的柔轮变形的基础。基于1.3节建立的实体有限元模型,在模型求解过程中保证波发生器长轴位置的径向变形量等于u0,从而获得装配状态下的周向位移。

2.2 单位啮合力引起的位移

在变形后的柔轮有限元模型上,沿柔轮齿啮合点切线方向逐一施加周向力(该周向力的幅值取额定扭矩下平均啮合力的3～5倍),提取所有啮合点处的周向位移,将其除以周向力幅值得到折算位移,即为折算单位力的柔度矩阵系数。图7所示为各啮合点的折算位移。

图7 啮合点的折算位移

图7中:横坐标为柔轮轮齿啮合点位置的极角,φ=0°为长轴;纵坐标为所有啮合点的周向位移。根据空载侧隙对应的极角范围,选取从长轴左侧φ=-21°至右侧φ=51°可能与刚轮啮合的柔轮轮齿范围。图7中的尖点表示在某个轮齿上施加单位啮合力时,该啮合点的周向位移。被施加啮合力的齿上的位移最大,其余齿的位移较小,距离施加啮合力的齿位置越远的齿,位移就越小。这是由于施加啮合力的齿上的啮合点位移由齿体变形和柔轮筒体变形组成,而其余齿的啮合点位移主要是由筒体变形引起。柔轮不同位置齿上的啮合点受单位啮合力时,产生的啮合点周向位移分布不同,表明不同位置齿的啮合刚度不同。

2.3 啮合刚度矩阵

根据第i个单位啮合力引起的第j个柔轮齿上啮合点的周向位移dij(j=1,2,…,n),循环i=1,…,n次得啮合柔度矩阵

(7)

D中各行元素分别表示在不同齿上施加啮合力时所引起的所有啮合点的周向位移,n为啮合点的数量。通过对柔度矩阵D求逆,可得啮合刚度矩阵

(8)

3 负载侧隙和啮合力迭代算法

3.1 啮合力迭代算法

在整个啮合过程中,波发生器和柔轮杯底固定,通过给刚轮施加逐渐增大的周向转动,来模拟谐波齿轮的负载传动状态。基于空载侧隙,求解负载工况下谐波齿轮的负载侧隙和啮合力分布。

首先定义啮合力数组{F}和柔轮啮合点位移数组{d},建立平衡方程

{F}=K{d}

(9)

当刚轮啮合点的周向位移大于该齿对的空载侧隙与柔轮啮合点的周向位移之和时,柔轮与刚轮啮合,反之处于未啮合状态。对于已啮合齿,柔轮啮合点的位移di等于刚轮啮合点的周向位移减去该齿对的空载侧隙,且该啮合点出现未知啮合力Fi。对于未啮合的齿,啮合力Fi为0,位移di未知。将以上数组元素代入式(9),利用迭代算法求解各啮合点的位移{di}与啮合力{Fi},迭代算法的流程如图8所示。具体步骤如下:

(1)设定初始数据,啮合齿数m=0,啮合齿的编号i=0,啮合齿编号数组N的所有元素置为0,刚轮转动的周向位移初始步长b=0.1 mm,最小迭代步长e=10-5mm;初始状态下全部齿未啮合,啮合力数组{Fi}为零;

(2)循环递增啮合齿数;

(3)循环递增刚轮转动的周向位移;

(4)求解平衡方程(9),得柔轮各啮合点的周向位移。

逐一判断刚轮上各啮合点的周向位移θm是否小于第i个柔轮啮合点的周向位移di与该齿对间的空载侧隙ci之和:若是,返回第(3)步循环;否则,判断步长b是否大于e,若是则令b=b/2返回第(3)步,否则表明第i个齿已啮合,保存该啮合齿编号。最后,判断负载扭矩是否小于额定扭矩:若是,返回第(2)步;否则,保存柔轮啮合点位移、负载侧隙和啮合力,迭代结束。

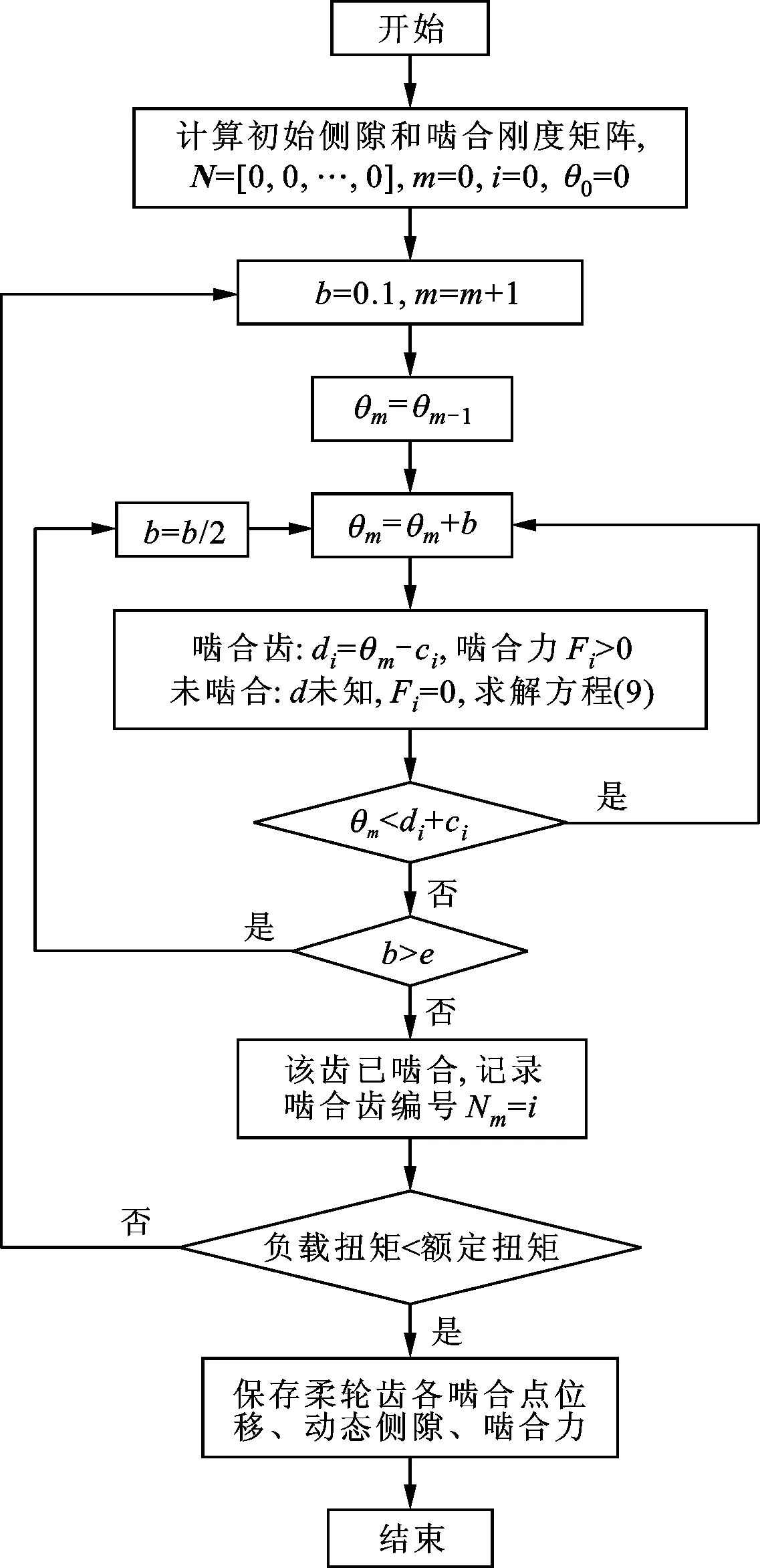
图8 迭代算法的流程图

由以上迭代算法可知,啮合齿数从0按步长1递增,直到负载扭矩达到额定扭矩。在此过程中,已啮合齿数不断增加,柔轮各啮合点的周向位移和啮合力在逐渐增大的刚轮啮合点周向位移作用下不断增大。

3.2 负载侧隙

不同负载下柔轮啮合点的周向位移和相对应的刚轮啮合点的周向位移不同,故负载工况下的侧隙是随负载大小变化的,本文定义其为负载侧隙。图9所示为本文算法计算的不同负载工况下的负载侧隙,图中:横坐标是柔轮啮合齿的位置极角,长轴处为0,顺时针为正;图例为施加在刚轮上的周向转角θ和刚轮上对应的负载扭矩T。

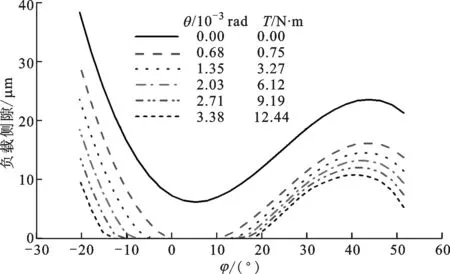
图9 本文算法计算的负载侧隙

由图9可知:长轴右侧φ=5°附近的空载侧隙最小,且首先降到0,表明此处的齿首先进入啮合;随着负载的增大,左右两侧齿的负载侧隙依次降为0,相继进入啮合;在φ=51°处齿的负载侧隙下降更快,当刚轮的周向转角达到3.38×10-3rad(相应的负载扭矩为12.44 N·m)时,负载侧隙降至5.34 μm。如果继续加大负载,该齿的负载侧隙会降为0,将发生齿廓干涉。

3.3 啮合力分布

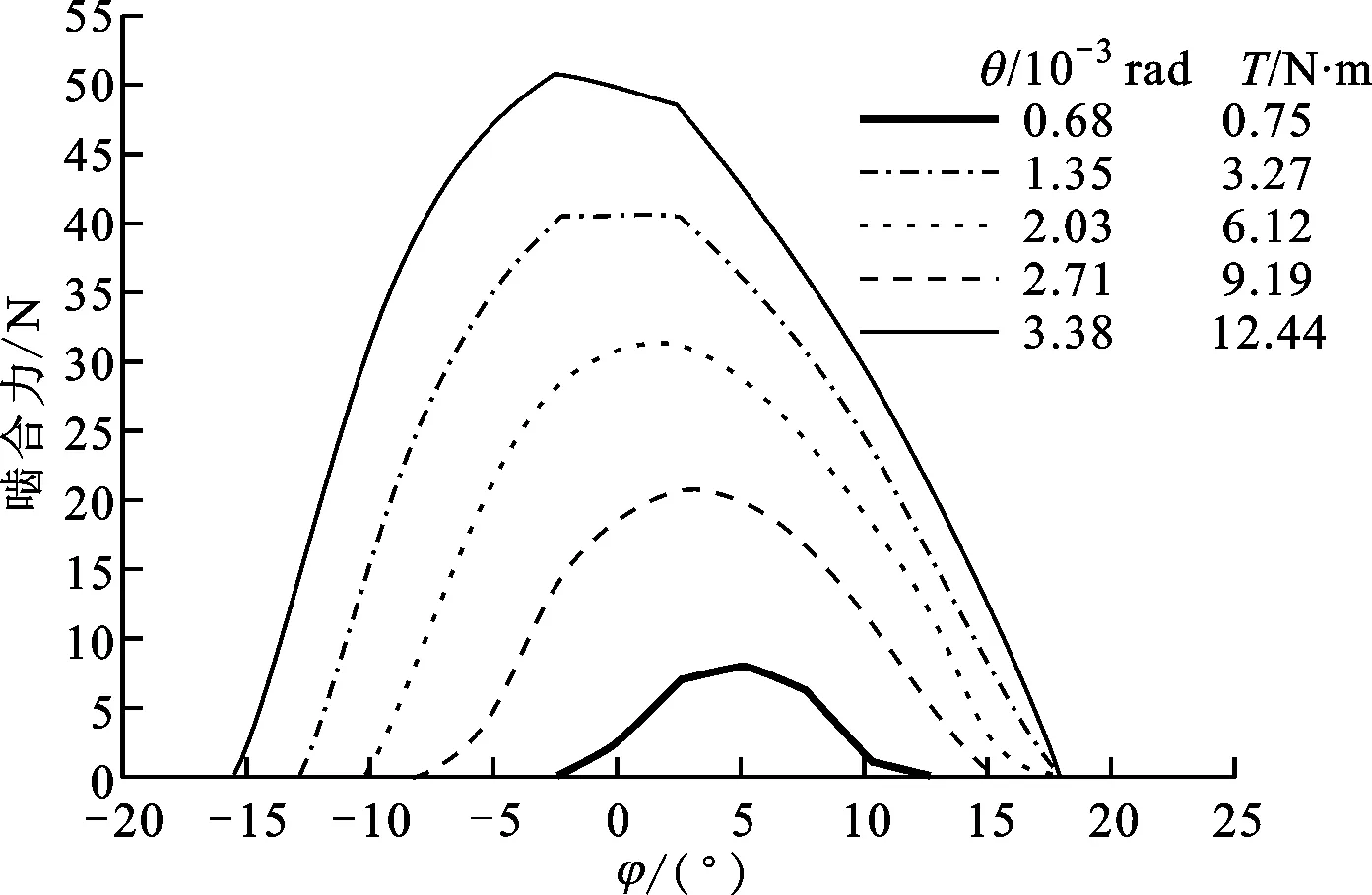
图10 本文算法计算的啮合力分布

图10给出了与图9相同负载下的啮合力分布,从中可以看出:在负载扭矩较小时,侧隙最小的齿(本算例约在φ=5°处)最先进入啮合,啮合力分布曲线在φ=5°处左右基本对称,最大啮合力为8 N;随负载增大,左右两侧的齿依次进入啮合,参与啮合的齿对数量增多,最大啮合力出现的位置逐渐向长轴左侧偏移;在刚轮的周向转角达到3.38×10-3rad(负载扭矩为12.44 N·m)时,最大啮合力幅值达到51 N。

4 啮合力的仿真验证

本文提出的啮合力和负载侧隙理论迭代算法所采用的线性啮合刚度矩阵,没有考虑啮合刚度随啮合力增大的非线性影响,特别是没有考虑不同啮合力作用于双圆盘波发生器使包角范围改变所引起的啮合刚度的非线性变化。为验证本文算法的有效性和适用范围,建立实体单元的有限元模型,利用有限元非线性接触分析方法,直接定义柔轮齿廓与刚轮齿廓间的接触关系,数值求解更贴近实际的啮合力和负载侧隙。

4.1 齿廓接触定义与接触分析

在有限元模型上的各啮合点的切线方向,定义三维点-点接触单元,可提高啮合齿面的接触计算效率。由柔轮啮合齿面上最小侧隙出现位置的分析可知,柔轮齿顶通常是最小侧隙点,因此首先定义柔轮齿顶点为接触单元端点。假定刚轮在传动过程中未变形,沿柔轮变形后齿顶矢径的切线方向,按照一定长度定义接触单元的另一端节点作为虚拟刚轮点。选用点-点接触单元CONTA178模拟啮合齿廓间的接触关系。选用增强拉格朗日接触算法,穿透容差小于10-5mm。每个接触单元的侧隙(GAP)设定为空载侧隙。

首先进行波发生器作用下的空载变形状态求解,随后移动虚拟刚轮点到达空载啮合状态。按照本文算法实例的刚轮传动位移,沿周向逐步移动虚拟刚轮点,施加与实例相同的刚轮啮合点周向位移,依次求解虚拟刚轮在不同传动状态时柔轮的变形和接触单元状态。

求解结束后,依次提取每个载荷步下接触单元的状态参数——接触力(PRES)和GAP,可获得接触面之间的法向接触力和负载侧隙。根据每个接触单元的状态参数,判断齿间啮合状态:对已啮合齿,PRES>0,GAP=0;对于未啮合齿,PRES=0,GAP<0。

4.2 有限元模型的负载侧隙和啮合力

图11是由有限元模型得出的负载侧隙曲线,实线为空载侧隙,其余曲线为不同负载下的负载侧隙。由于有限元模型的啮合刚度是非线性的,所以图11中的负载扭矩值与图9、图10中的略有不同。由图11可知:在长轴右侧φ=5°附近,负载侧隙首先降到0;随负载的增大,左右两侧的齿的负载侧隙依次降至0,表明这些齿已进入啮合,但长轴左侧的齿的负载侧隙下降更快;在刚轮转角为3.38×10-3rad(负载扭矩为11.19 N·m)时,左侧φ=-13°处齿的负载侧隙为0,表明该齿进入啮合,此时最右侧φ=51°处齿的负载侧隙为4.96 μm。

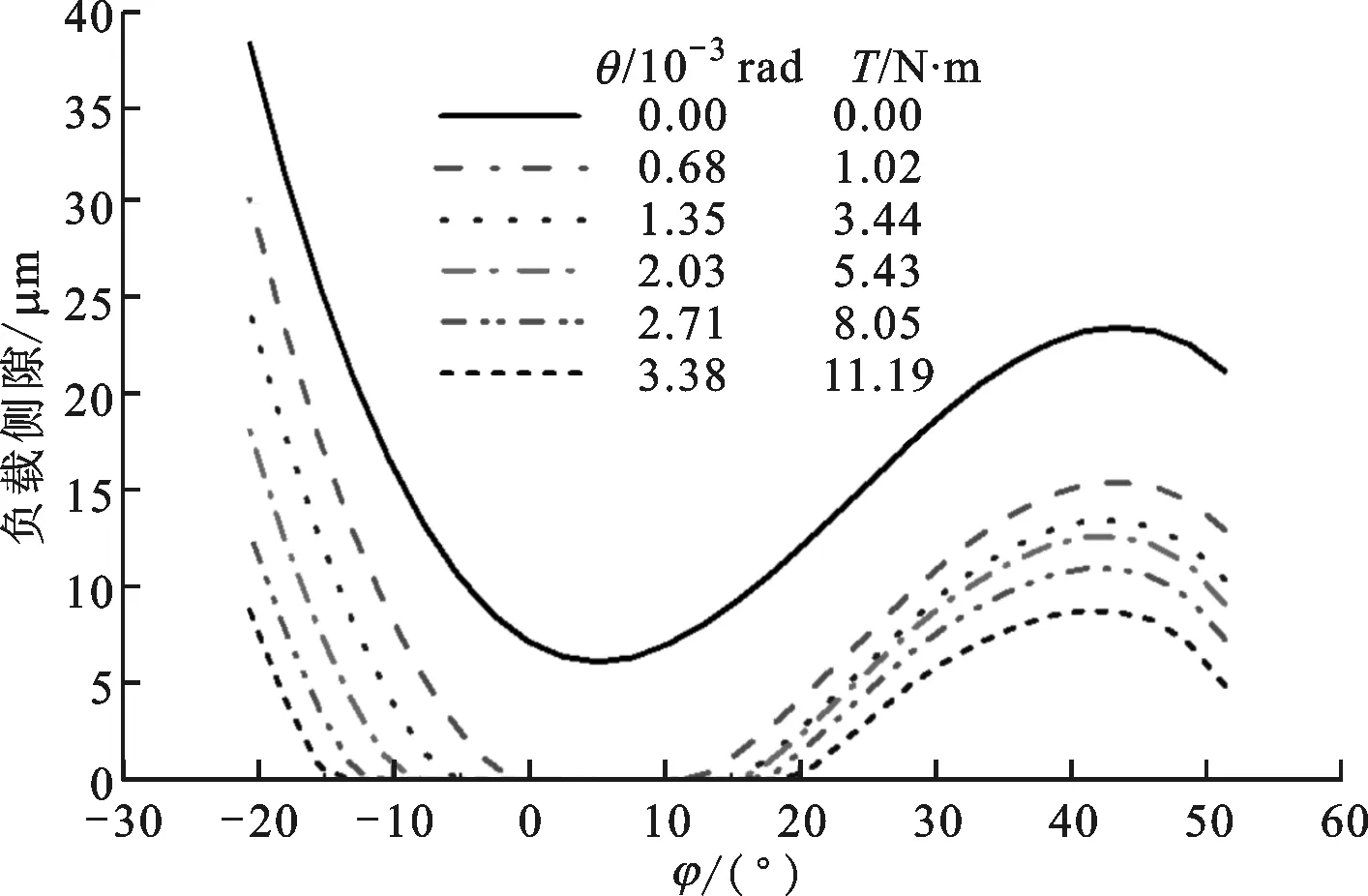
图11 用有限元模型求得的负载侧隙曲线

图12为由有限元模型求得的啮合力分布曲线,可以看出:当负载扭矩较小时,在空载侧隙最小的位置φ=5°处,齿出现了啮合力,在-5°≤φ≤15°区间上关于φ=5°基本对称分布,最大啮合力为9.6 N;随负载增大,左右两侧参与啮合的齿逐渐增多,最大啮合力的位置向左明显偏移,在刚轮转角为3.382×10-3rad(负载扭矩为11.19 N·m)时,最大啮合力位置向左偏移了8°,最大啮合力幅值达到43 N。

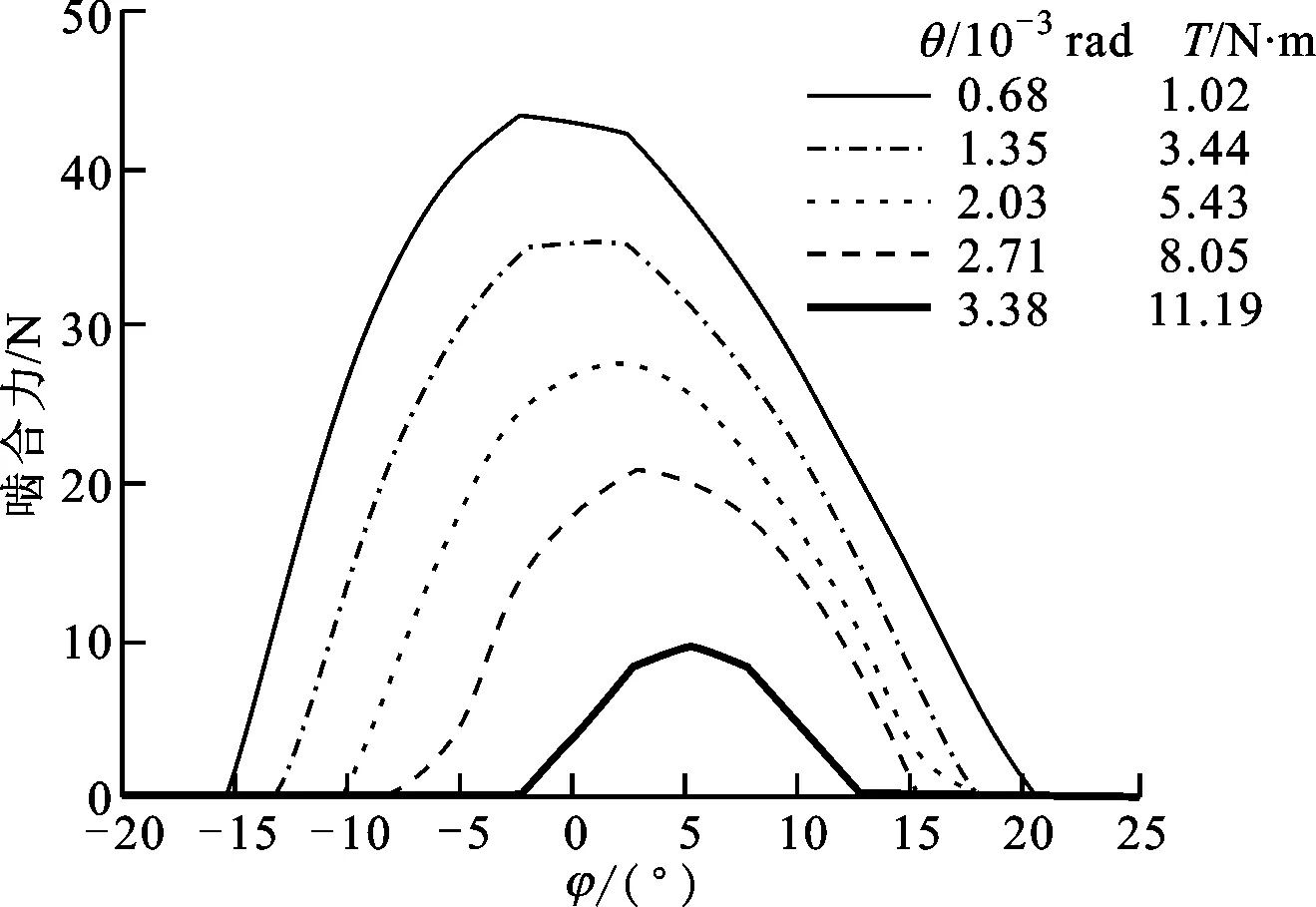
图12 由有限元模型求得的啮合力分布

5 本文算法和有限元分析的比较

5.1 负载侧隙比较

对比图9和图11发现:负载侧隙的本文算法理论解和有限元解吻合得很好;在长轴右侧φ=5°附近空载侧隙最小处,负载侧隙首先降为0,表明该齿首先进入啮合;随着刚轮转角的增大,左右两侧的齿的负载侧隙逐渐降为0,表明该部位的齿相继进入啮合;在刚轮转角为3.38×10-3rad时,理论解和有限元解的啮合区间都为-13°≤φ≤18°;在φ=-21°和φ=51°处有限元解的负载侧隙都小于理论解的负载侧隙,侧隙差值分别为1.04 μm和0.38 μm,表明有限元解的负载侧隙比理论解下降得快,在长轴左侧下降得更快,但差异不大。

5.2 啮合力分布对比

对比图10和图12发现:在刚轮转角不大时,啮合力的本文算法理论解和有限元解关于φ=5°左右对称分布,区间相同,但理论解的啮合力小于有限元结果,表明小负载时相比于有限元解,理论解的刚度偏小;随着刚轮转角的增大,2种方法的最大啮合力位置均向长轴左侧偏移了8°,啮合力分布区间相同,但有限元解的啮合力幅值低于理论解;至最大刚轮转角时,理论解的最大啮合力比有限元解的大17%左右,表明大负载时理论解的刚度略大于有限元解。

5.3 单齿啮合力分析

为定量分析本文算法理论解的啮合力与有限元解的差异,给出了2种算法得出的最先进入啮合的2对齿(分别为波发生器长轴右侧的第3号齿和第4号齿)上啮合力随刚轮转角的变化曲线,如图13所示。

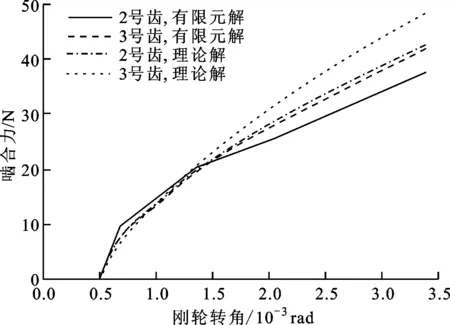
图13 本文算法与有限元分析得出的单齿啮合力曲线

由图13可以看出:在刚轮转角小于1.5×10-3rad的低负载工况下,2个啮合点上理论解与有限元解的啮合力吻合良好,但随刚轮转角的增大,单齿啮合力的理论解大于有限元解。这是由于随着负载的增加,有限元模型的啮合刚度呈非线性变化并略有下降所致。

5.4 扭转刚度对比

图14所示为理论解与有限元解的负载扭矩-刚轮转角曲线。转角0.45×10-3rad为刚轮的空程转角,此时轮齿刚进入空载的啮合状态。去除刚轮转过的空程,曲线的斜率为扭转刚度。

从图14可以看出:理论解的扭转刚度为常数;在刚轮转角小于1.5×10-3rad的低负载工况下,负载扭矩与刚轮转角呈现线性关系,有限元解与理论解吻合良好;随刚轮转角的增大,有限元解的扭转刚度呈现非线性,理论解的扭转刚度大于有限元解,但2种方法的负载扭矩偏差不大,在刚轮最大转角时的扭矩偏差约为11.21%。

通过查阅Harmonic Drive组件型产品综合目录得知,本文算例的额定扭矩在7 N·m左右。由图14可知,对于12 N·m以下的负载扭矩,本文算法给出的扭转刚度与有限元分析的结果基本吻合。

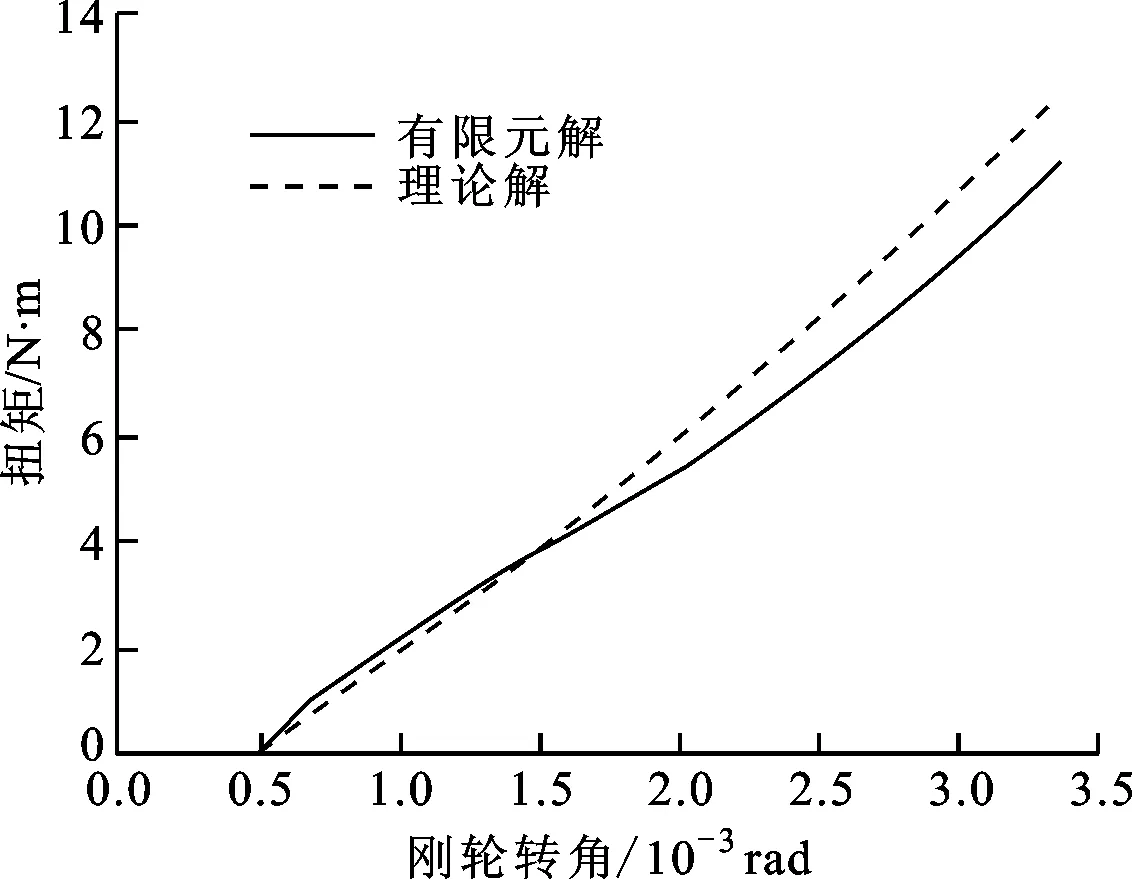
图14 本文算法与有限元分析得出的负载扭矩-刚轮转角曲线

6 结 论

(1)在低负载工况下,单个齿上的啮合力与刚轮转角呈现线性关系;随负载的增大,单个齿上的啮合力与刚轮转角呈现非线性关系。

(2)啮合力分布关于最小侧隙位置左右基本对称;当负载较大时,轮齿的啮合刚度非线性变化显著,最大啮合力位置向左侧明显偏移。本文理论算法得到的轮齿啮合刚度偏大,故其啮合力幅值总体高于有限元模型的。

(3)在额定扭矩下,本文算法给出的扭转刚度与有限元分析给出的非线性结果基本吻合。