基于粗糙集和遗传算法的中医方证相关性研究

陈建国 李四海 赵 磊

1(甘肃中医药大学信息工程学院 甘肃 兰州 730000) 2(甘肃省高校中(藏)药化学与质量省级重点实验室 甘肃 兰州 730000)

0 引 言

辨证论治是中医认识疾病和治疗疾病的基本原则，是中医对疾病的一种认识和处理方法，“方证相应”则是中医辨证论治的核心环节。方即是方剂，是药味有效作用于证的连接点和桥梁。证是对疾病发展特定阶段所呈现病理反映的抽象和概括，包括病变的原因、性质、部位及对立关系，反映这一阶段病理变化的本质。与疾病的具体症状相比，证能更全面、更深刻、更系统地揭示疾病的本质。所谓“方证相应”指的是一个方剂的药味、配伍关系、主治功效和该方剂所对应的证之间存在高度的统一性和针对性[1]。方与证对应程度越高，则疾病的治疗效果越好，反之则治疗效果越差，研究方证之间的对应关系对于实现辨证论治及临床选方用药都具有重要意义[2]。

粗糙集[3]是由波兰数学家Z.Pawlak于1982年提出的一种处理不精确、不完备、不相容数据的数学工具。其主要思想是将不精确或不确定的知识用已有知识库中的知识来近似表达，属性约简是粗糙集理论的核心内容。在保持决策系统分类能力不变的前提下，删除不相关或不重要的条件属性，简化计算过程，得到问题决策规则的过程被称为属性约简。将粗糙集与神经网络、支持向量机、模糊集、遗传算法等机器学习方法相结合，可有效解决近似推理、金融数据分析、图像处理、医疗诊断等领域中的知识发现问题。

从信息处理的角度来看，中医辨证论治过程可归纳为首先通过四诊获取病人的症状信息建立知识库，然后根据专家知识和经验对疾病证候或证型进行人工推理决策的过程，这与粗糙集理论中的知识获取和决策推理过程有相似之处。近年来，粗糙集被逐渐用于中医药研究领域，文献[4]运用粗糙集分析了方剂和症状之间的相关性，通过属性约简，提取了方剂所对应的核心症状集。文献[5]建立了中药性味归经和其祛风湿功效的支持向量机预测模型，通过粗糙集属性约简消除了冗余属性，降低了模型的复杂度。文献[6]基于粗糙集理论对中药复方药物的重要性进行了评价，其评价效果优于传统的频次统计方法。以上研究中决策表的论域及属性集规模较小，属性约简都是根据定义直接进行约简，无法有效解决大规模决策表的属性约简问题。

本文收集治疗心率不齐(心悸)及心绞痛(胸痹)的冠心病方剂共165首，建立方剂和证型之间的决策表，使用改进的遗传算法进行属性约简，提取了方证之间的决策规则，对方证规则的合理性进行了分析。

1 粗糙集理论[7]

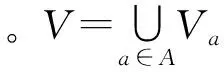
定义2对于决策表DT=(U,C∪D,V,f)，若B⊆C，则B对应的不可辨识关系定义为：

Ind(B)={(x,y)|(x,y)∈U2,∀b∈B(b(x)=b(y))}

如果(x,y)∈Ind(B)，则称x,y是基于B不可分辨的。以U/Ind(B)表示不可辨识关系Ind(B)在U上导出的所有等价类。[x]Ind(B)为基于B得到的x的等价类。

定义3给定对象集合X⊂U，属性集合B⊆A，Ind(B)为不可辨识关系，则X关于B的下近似为：

定义4决策属性D关于条件属性C的正域为：

定义5决策属性D对条件属性C的依赖度定义为：

定义6R是一个等价关系簇，I∈R，若Ind(R)=Ind(R-{I})，则称I在等价关系簇R中是不必要的，否则称I为R中必要的。如果R中的每一个等价关系I都是必要的，则称I是独立的，否则称I为依赖的。

定义7对于决策表DT=(U,C∪D,V,f)，B⊆C，如果B独立且Ind(B)=Ind(C)，则称B是C的约简，记为red(C)。

定义8核属性定义为：core(B)=∩red(B)，其中red(B)表示B的所有约简。

2 属性约简算法

属性约简是粗糙集理论主要的研究内容之一[8]，由于求解决策表的最小约简和所有约简是NP-hard问题，因此一些智能优化算法被用于决策表的属性约简[9-10]。遗传算法是由美国Michigan大学的Holland教授提出的一种解决最优化问题的启发式搜索算法，具有搜索范围广、自组织、自适应、鲁棒性及可扩展性强等特点，已被广泛用于机器学习、信号处理、组合优化等领域，在粗糙集属性约简中也已经得到成功应用[11]。

2.1 算法描述

2.1.1 编码方法

种群个体采用二进制位串的编码方式，每一个二进制位代表一个条件属性。假设条件属性集合为C={C1,C2,…,Cm}，则二进制编码的长度为m，用0表示对应的条件属性被约简，用1表示对应的条件属性被保留。

2.1.2 适应度函数

适应度函数是评价个体优劣和选择个体的重要依据，由属性约简的定义，个体的适应度函数要考虑两个方面的要求：(1) 个体包含的条件属性个数。个体中二进制编码1的个数越少，个体被选择的概率越大，得到的约简也越接近最小约简。(2) 个体的分类能力。属性约简与原条件属性集的分类能力应该相当。一般用决策属性对条件属性的依赖度来度量个体的分类能力。为构造适应度函数，首先进行如下定义。

定义1个体稀疏度定义为：

(1)

式中:j=1,2,…,n，n为种群大小，ρj表示个体中没有包含的属性的比率。个体包含的属性个数越少，ρj越大，个体稀疏度越高。

定义2个体稀疏度的KL散度定义为：

(2)

式中:ρj为个体j的稀疏度，ρ为期望稀疏度。ρ的作用在于控制对个体的惩罚力度，ρ越小，惩罚力度越大。图1给出了ρ分别为0.2和0.5时，个体稀疏度的KL散度曲线。

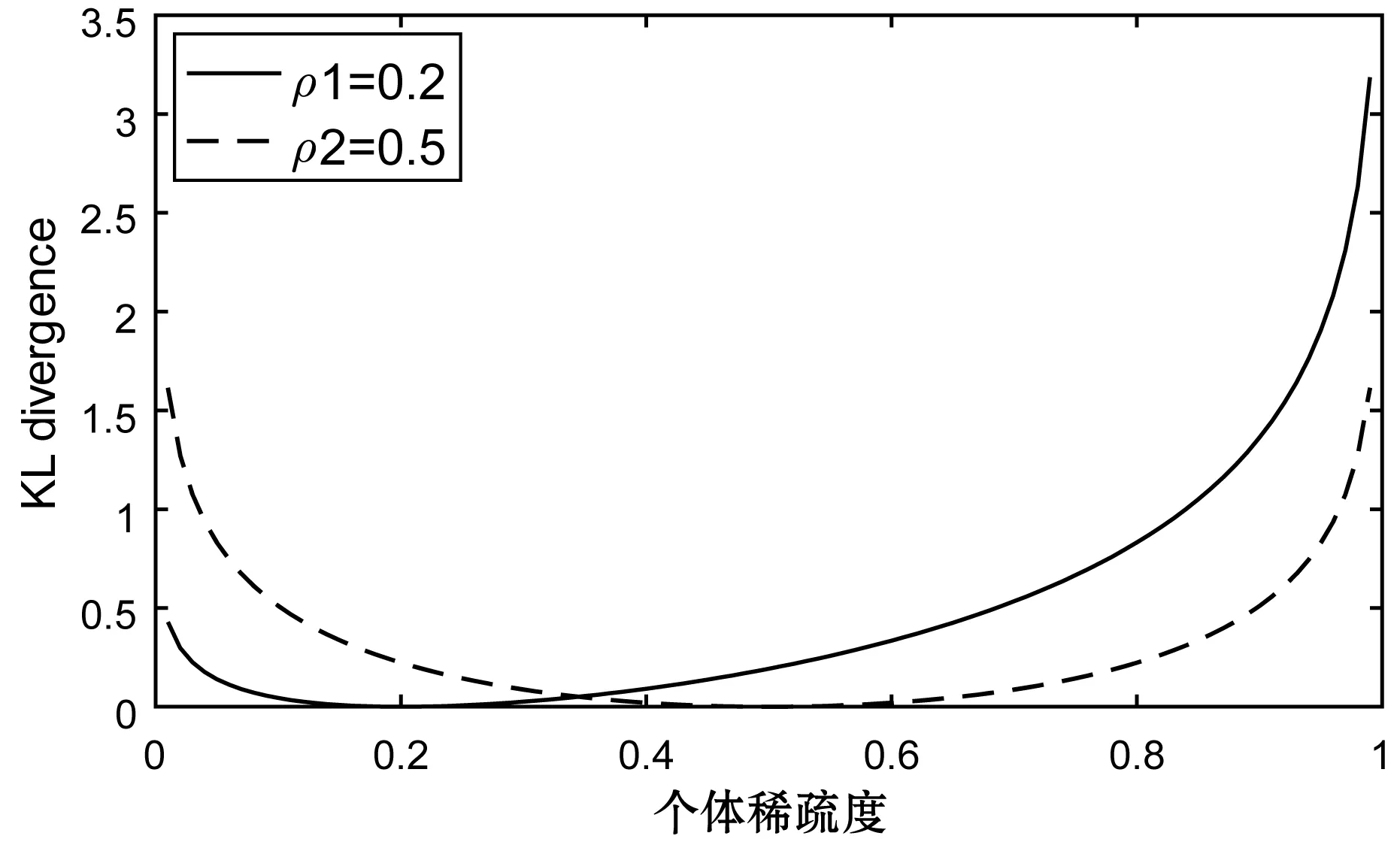
图1 个体稀疏度的KL散度曲线

由图1可知，个体包含的属性越少，其稀疏度越高，KL散度值也越大。因此，通过最大化KL散度能够保留稀疏度较高的个体，抑制稀疏度较低的个体，得到最小约简。考虑到种群为随机初始化，个体稀疏度接近0.5，当ρ=0.5时，惩罚力度明显不够，得不到最小约简，减小ρ则能够相应地增大惩罚力度，因此，一般设置ρ<0.5，其最优值通过实验确定。

定义3适应度函数定义如下：

(3)

该函数由两部分组成，第一部分是目标函数，其含义为决策属性D对个体xj的依赖度。依赖度值越大，表明个体的分类能力越强。最大化决策属性对个体的依赖度，可以使个体搜索总在可行解空间上进行。

适应度函数第二部分为惩罚项，KL(ρ‖ρj)表示个体稀疏度的KL散度，用于对包含条件属性较多的个体进行惩罚。个体包含的属性越多，其稀疏度值越小，KL散度值也越小，则适应度函数值越小。反之，个体包含的属性越少，其稀疏度值越大，其KL散度值越大，则适应度函数值越大。最大化KL散度值将能够使稀疏度高的个体受到保护，稀疏度低的个体受到抑制，使搜索总在最小约简的方向进行。β为稀疏惩罚因子，用于权衡分类能力和稀疏度之间的相对重要性。

2.1.3 选择算子

选择算子决定了个体以多大的概率值被选择，是评价父代种群中个体优劣的重要依据。使用比例选择算子，通过轮盘赌的方式选择优质个体。对于种群规模为n的父代种群{x1,x2,…,xn}，个体xi被选择的概率值为：

(4)

2.1.4 交叉算子

交叉算子用于提高种群个体的多样性，采用单点交叉算子，以一定的交叉概率pc选择参与交叉的个体。个体交叉位随机选择，交换两个父代个体在交叉位左右的子串，产生下一代个体。

2.1.5 变异算子

采用基本位变异算子,具体过程为：根据变异概率pm产生满足数量要求的变异点，对每一个指定的变异点，对其基因位进行取反运算，从而产生出一个新的个体。

2.2 算法流程

算法遗传属性约简算法

输入：一个决策表DT=(U,C∪D,V,f)，期望稀疏度ρ，稀疏惩罚因子β；

输出：决策表的一个最小约简。

Setp1随机产生n个长度为m的二进制位串x1,x2,…,xn，得到初始种群。

Setp2根据设置的期望稀疏度ρ及稀疏惩罚因子β，按照式(3)计算个体的适应度函数值。

Setp3根据个体的适应度值，利用式(4)计算个体被选择的概率，然后通过轮盘赌的方式实现个体的选择。

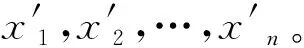
Setp6如果连续t=10代内种群中最优个体的适应度值没有改变或已经达到设定的最大进化代数T=30，则终止进化，输出最优个体。

3 实验结果及分析

3.1 方证决策表的建立

收集整理中医治疗冠心病的有效方剂165首，共涉及中药319味。每一首方剂均具有明确的主治证型，其中85首主治证型为心绞痛(属于中医胸痹、心痛范畴)，80首主治证型为心率不齐(属于中医心悸范畴)。对方剂中的中药药名进行统一规范处理，统计每一味中药出现的频次，按频次大小进行降序排列，中药药名分别用C1、C2、…、C319表示。如：C1=丹参、C2=黄芪、C3=川芎、C4=炙甘草、C5=当归。对方剂进行离散化处理，某一味中药在方剂中出现则对应的条件属性取值为1，否则取值为0，方剂主治证型为决策属性，用0表示心绞痛，1表示心率不齐，建立方证决策表。表1给出了冠心病方证决策表的部分内容。

表1 冠心病方证决策表

3.2 属性约简结果

对方证决策表使用文中给出的遗传算法进行属性约简。遗传算法的参数设置：种群大小m=200，交叉概率pc=0.8，变异概率pm=0.03，进化代数T=30，期望稀疏度ρ=0.05。

由适应度函数的定义可知，算法的关键参数主要有两个：期望稀疏度ρ和稀疏惩罚因子β，其中ρ控制对个体稀疏度的惩罚力度，为获得最小约简，ρ一般取较小值。本文经过多次实验，当ρ=0.05时能够获得较好的惩罚效果。

在确定惩罚力度的情况下，属性约简结果主要与稀疏惩罚因子β有关。β的作用在于权衡分类能力和个体稀疏性之间的相对重要性，并在二者之间取得平衡。图2给出了当ρ=0.05时，稀疏惩罚因子β和属性约简结果之间的关系曲线。

图2 惩罚因子对约简结果的影响

由图2可得，当惩罚因子β=0.5时，决策属性对约简结果的依赖度取得最大值0.987 88，此时C_reduct包含的条件属性数为24个。β越小，表示属性约简更重视个体的分类能力，约简结果所含有的属性个数会越多，则决策属性对约简结果的依赖度也会相应增大；反之，β越大，随着惩罚项在适应度函数中作用的提升，表示属性约简更重视得到最小约简，约简结果中所含有的属性个数会相应地减少，则决策属性对约简结果的依赖度也会相应减小。

根据以上分析，设置β=0.5，其他参数设置不变，图3给出了遗传算法的进化曲线。最后得到的属性约简中包含24味中药，分别为{丹参、黄芪、川芎、延胡索、当归、麦冬、桂枝、茯苓、赤芍、瓜蒌、党参、桃仁、红花、薤白、五味子、三七、细辛、制附子、陈皮、葛根、炒酸枣仁、炙甘草、苦参、鸡内金}。

图3 遗传算法进化曲线

3.3 决策规则及分析

根据置信度和覆盖度对得到的决策规则进行筛选。置信度定义为规则左侧对规则右侧的条件概率，覆盖度定义为决策规则的对象数占论域空间中对象数的比例[12]。表2为筛选出的4条决策规则。

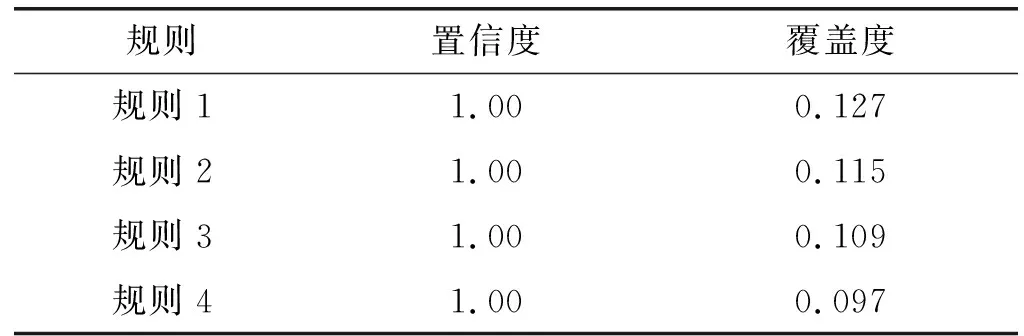
表2 决策规则筛选结果

规则1：麦冬 AND 桂枝 AND 党参 AND 红花 AND 三七 ->心率不齐

规则2：黄芪 AND 桂枝 AND 茯苓 AND 五味子 AND 葛根 ->心率不齐

规则3：丹参 AND 黄芪 AND 川芎 AND 茯苓 AND 赤芍 AND 陈皮 ->心绞痛

规则4：黄芪 AND 川芎 AND 当归 AND 茯苓 AND 赤芍 ->心绞痛

可以看出，规则1和规则2中的药物主要以益气、养阴为主，规则3和规则4中的药物主要以活血化瘀为主。冠心病属于中医胸痹、心痛范畴。文献[13]认为心悸(心率不齐)的病机为气阴两虚、痰瘀互结，其治疗主要以益气、养阴和安神为主，兼顾祛痰化瘀，实现标本兼治，在用药方面：益气药物有黄芪、党参等，养阴和安神药物有麦冬、五味子、炒酸枣仁等，祛痰化瘀药物有瓜蒌等。冠心病心绞痛为本虚标实之证，益气、活血、化瘀是冠心病心绞痛的基本治疗方法，在用药方面：活血化瘀药是治疗冠心病的首选药物[14]，常用的活血化瘀药物有丹参、川芎、红花、桃仁、延胡索、赤芍等。可以看出，本文得到的方证规则与中医治疗两种冠心病的用药方法基本一致。

4 结 语

提出了一种基于改进遗传算法的决策表属性约简算法，构造了新的适应度函数，一方面通过最大化决策属性对条件属性的依赖度保证了分类能力，同时为获得最小约简，对包含属性较多的个体进行惩罚，使搜索沿着最小约简的方向进行。使用该方法对冠心病方证决策表进行了属性约简，所提取的规则与中医对心率不齐及心绞痛两种类型的冠心病的认识与用药原则基本一致，说明本文的方法是合理和有效的。

文中提出的属性约简算法中惩罚因子对约简结果影响较大。此外，通过提前确定核属性，在个体的变异操作中对核属性对应的基因位不进行变异将能够进一步加快遗传算法的收敛速度。如何快速有效地选择惩罚因子及加快遗传算法的收敛速度将是下一步要解决的问题。