基于差异性和准确性的加权调和平均度量的基因表达数据选择性集成算法

高慧云，陆慧娟，严 珂，叶敏超

(中国计量大学信息工程学院，杭州310018)

(*通信作者电子邮箱hjlu@cjlu．edu．cn)

0 引言

癌症是威胁人类公共健康的主要疾病之一，且死亡率较高，如果能及早发现癌症疾病并及时治疗将有利于患者的康复［1］。目前，基因表达数据已普遍应用于癌症分类，通过利用机器学习的方法对基因表达数据进行处理分析，这种新方法有望通过对癌症的精确诊断为癌症患者提供更好的治疗。基因表达数据是通过DNA微阵列杂交实验得到的，其数据具有高维、小样本、高噪声等特点，使通过机器学习算法对癌症基因的诊断变得困难。

目前，机器学习的主要发展之一就是集成学习，集成学习是一种通过结合多个基分类器以提高整体泛化性能的算法［2］。常 见 的 集 成 学 习 算 法 有 Bagging［3］、Boosting［4］等。Tumer等［5］指出基分类器之间的差异性和基分类器自身的准确性是决定集成系统泛化性能的两个重要因素;周志华［6］也提出基分类器的差异性越大、准确性越高，则集成的效果越好;张春霞等［7］指出基分类器的差异性难以衡量，现有的选择性集成算法大多只考虑到基分类器之间的差异性而忽略基分类器自身的准确性;陆慧娟等［8］提出了一种输出不一致测度的选择性集成算法，通过删除相似度较高的基分类器来保证基分类器之间的差异性;Margineantu等［9］指出，基分类器的差异性和准确性这两个因素彼此相互制约;为克服平衡基分类器的差异性和准确性的困难，Mao等［10］提出一种通过最大化三个不同二次形式来对基分类器中的进行加权的新方法，通过最小化集合误差得到个体分类器的最佳权重。

超限学习机(Extreme Learning Machine，ELM)是2006年Huang等［11］提出的一种单隐层的前馈神经网络，该算法以极快的学习速度和较好的泛化性能得到人们的广泛关注。但单个ELM仍存在分类精度较差、训练结果不稳定等缺点。本文采用核超限学习机(Kernel Extreme Learning Machine，KELM)作为集成学习算法的基分类器，同时考虑基分类器之间的差异性和准确性，提出一种基于差异性和准确性的加权调和平均(Diversity-Accuracy-Weighted Harmonic Average，D-AWHA)度量的选择性集成算法，从UCI标准分类数据集中选择了乳腺癌Breast、肺癌Lung、卵巢癌Ovarian三种基因数据进行实验仿真，实验结果表明该算法为癌症基因表达数据的分析提供了一种有效的方法。

1 核超限学习机

ELM是单隐层的前馈神经网络训练算法，根据Huang等［12］提出的ELM理论，ELM的主要目的是同时减少训练误差和输出权重的范数。在传统的ELM框架和最小二乘损失函数中，最小化训练误差ζi和输出权重的范数可表示为:

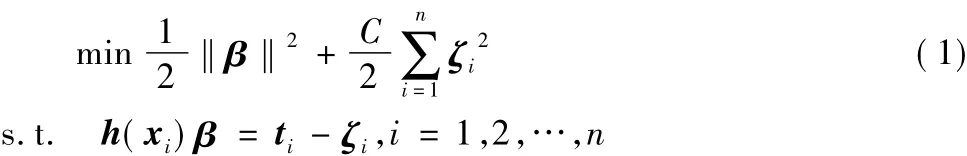
其中:β是输出权重，C是惩罚参数，ζ是训练集的训练误差矩阵，h(x)表示的是隐藏核映射，t是已标记样本，n为样本数。根据KKT理论，训练ELM等价于解决如下对偶问题:

其中:拉格朗日乘子αi对应第i个训练样本，因此，本文可以得到KKT(Karush-Kuhn-Tucker)最优条件:

其中:α = ［α1，α2，…，αn］T，H 为隐层输出矩阵，因此式(3)可等价为:

其中:I是单位矩阵。T可表示为:

因此，式(1)中最优β可以通过分析获得:

根据Mercer定理，任何半正定函数都可作为核函数，因此KELM的核矩阵可表示为:

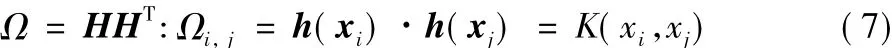
其中:i，j∈ (1，2，…，N)，K(xi，xj) 是核函数。

常见的核函数有:

1)RBF核函数(Radical Basis Function Kernel):

2)线性核函数(Linear Kernel):

3)多项式核函数(Polynomial Kernel):

本文采用RBF核函数，核函数参数δ为默认值类别数的倒数。

因此，KELM的实际输出可表示为:

2 选择性集成

一般来说，一个集成算法分为两个步骤:首先生成多个基分类器，然后通过某种结合策略将它们结合起来。根据文献［6］，集成学习算法按照基分类器的生成方式大致可分为Bagging和 Boosting两类。2002年，Zhou等［13］首次提出了选择性集成的概念，并指出选择集成系统中部分基分类器进行集成不仅能提高算法的速度，而且能提高集成系统整体的泛化性能。因此选择性集成是一种特殊的集成学习方式，它旨在使用更少的基分类器达到更好的泛化能力，被认为比单一的分类算法和传统的集成算法更有效。目前，许多选择性集成方法被提出，如徐晓杨等［14］提出一种基于ELM的选择性集成分类算法，Guo等［15］提出基于动态粗糙子空间的选择性集成，Zhu等［16］提出基于改进的人工鱼塘算法的ELM选择性集成，都证明部分集成的效果优于全部集成。根据文献［5］的内容，基分类器之间的差异性和基分类器自身的准确性是决定一个集成系统泛化性能的两个重要因素，因此，如何选择一组差异性高并且分类精度高的基分类器是本文的重点。

2．1 差异性度量

基分类器之间的差异性是决定一个集成系统泛化性能的关键因素，但测量基分类器之间的差异性不简单，目前还没有统一的定义形式。Kuncheva等［17］提出了10种度量基分类器之间差异性的方法，包括4种基于对(pair-wise)的方法:Q统计量(Q statistic)、相关系数(correlation coefficient)、不一致性度量(disagreement)和双误性(double fault)以及6种非基于对(non-pair-wise)的方法:投票熵(entropy of votes)、困难索引值(difficulty index)、Kohavi-Wolpert方差、评论一致性(interrater agreement)、泛化差异性(generalized diversity)和同步失败差异性(coincident failure diversity)。考虑到基于对的差异性度量的计算复杂度较小，本文将采用基于对的差异性度量。

假设标签数据集 D={d1，d2，…，dN}，对于二分类任务zj∈{0，1}，基分类器hi、hj的分类结果关系表如表1所示。

表1中N=N11+N10+N01+N00，N11表示基分类器hi和hj都分类正确，因此对于基分类器hi和hj，上述4种基于对的差异性度量方法Q统计量、相关系数ρ、不一致性度量D和双误性度量DF可分别表示为:

从式(12)～(13)可以看出，当基分类器hi和hj共同分对或者分错的越多时，Q统计量和相关系数ρ越接近1;反之如果两个基分类器对同一样本分出的不一致的结果越多则越接近－1。不一致性度量D是直接测量两个基分类器对同一样本分类结果不同的测度，当基分类器同时分对或分错时就越接近0，反之越接近1。双误性度量DF表示两个基分类器同时将样本分错与总样本数的占比。

因本文对基分类器之间的差异性的度量主要是考虑单个基分类器与其他基分类器分类结果之间的差异，并不只是考虑分错的情况，因此将不采用双误性度量这一评价标准。因上述其他3种差异性度量方式的侧重点不同，本文将综合这3种测量方式对各个基分类器进行度量，考虑到Q统计量和相关系数ρ的值域是［－1，1］，且值越小，基分类器之间的差异性越大，因此本文将采用sigmoid函数对其结果进行处理:

在实验中，本文将对每个基分类器的分类结果与其他所有的基分类器分类结果比较进行差异度计算，使用DIVi，j作为最后基分类器之间差异性度量，计算公式为:

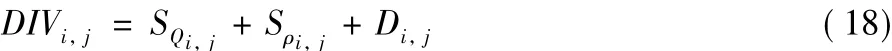
2．2 D-A-WHA 度量

差异性一直被公认为是提高一个集成系统泛化性能的重要因素，因为如果基分类器之间是高度相关的，将它们结合以后也很难得到更好的分类结果;而如果基分类器的分类精度非常准确，这就意味着基分类器的相似度将很高，因此差异性也就较差［18］。吴建鑫等［19］提出集成泛化误差公式:

为找出集成系统中差异性较大并且精度较高的基分类器，本文提出一种基于D-A-WHA度量的选择性集成算法，通过对集成系统中所有的基分类器的差异性和准确性的量化，利用加权调和公式将多样性和准确性有效结合，保证挑选出来的基分类器在保证准确性的同时差异性也大。为均衡基分类器之间的差异性(Diversity)和单个基分类器的准确率(Accuracy)对差异性和准确性进行归一化:

因此第i个基分类器的差异性和准确率的调和平均数(Harmonic Average，HA)可定义为:

因为在不同的数据集和生成的不同基分类器的情况下，基分类器之间的差异性和基分类器本身的准确率对一个集成系统泛化性能的影响不一定相同，且基分类器之间的差异性很难被准确量化，需要对差异性和准确率设置权重进行调节，因此D-A-WHA度量可定义为:

当ε=1时，公式退化为式(22)，当ε越大时差异性影响越大，ε越小时准确率影响越大。

3 算法描述

通过以上分析，D-A-WHA选择性集成算法的目的是选择出一组差异性较大并且分类精度较高的基分类器进行集成，D-A-WHA的算法描述如下:

1)设置训练的分类器个数n和挑选的基分类器个数m;

2)将原始数据分为训练样本和测试样本，并使用n个KELM对训练样本进行训练;

3)计算出每一个分类器的分类精度A和每一个分类器i对每个样本的分类结果;

4)计算分类器的差异性D;

5)将分类器的准确性A和差异性D归一化，按照式(23)计算每个基分类器的D-A-WHA度量;

6)取D-A-WHA度量前m的基分类器进行集成。

7)使用选择的部分基分类器对测试样本进行测试;

8)多次实验求平均值。

算法流程如图1所示。

图1 基于D-A-WHA选择性集成的流程Fig．1 Flow chart of selective ensemble based on D-A-WHA

4 实验

4．1 实验数据

为评估基于D-A-WHA测度的选择性集成算法的性能，本文对该算法进行了实验分析与仿真。本文在公开的UCI数据集中选择了乳腺癌Breast、肺癌Lung和卵巢癌Ovarian三种基因数据集进行实验和对比。因基因数据集样本数小，但维度较高，在不进行处理的情况下能到达上万维，因此在对数据进行分析之前要先对数据集进行ReliefF［20］降维，降维后的数据集基本信息如表2所示。

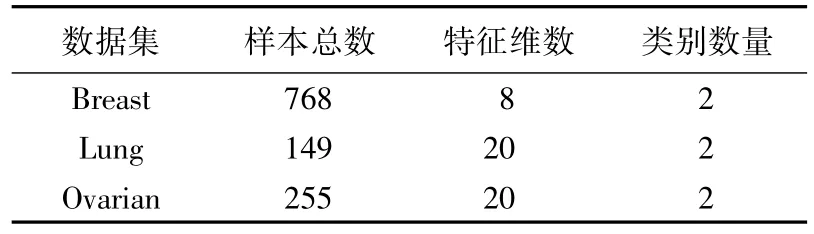
表2 数据集信息Tab．2 Data set information

4．2 实验结果

本文将实验中的KELM的隐藏节点数统一设为10，正则化系数为2，激活函数采用是的sigmoid函数。为避免算法的不稳定性，所有实验结果将取迭代30次的平均值。为了寻找在不同数据集中D-A-WHA的最优权重ε，实验在相同的基分类器个数下(基分类个数设为10)，多次取值找到最优权重ε。图2展示Breast数据集在ε不同取值时的精度，从图中可以看出在ε为1时分类精度最高;按上述方法得到在Ovarian和Lung数据集中，权重ε分为1．7和1．5时集成效果较好。

图2 Breast数据集下不同ε值分类精度的关系Fig．2 Relationship between classification accuracy and ε value on Breast dataset

为验证基于D-A-WHA测度的选择性集成算法的性能，将本文算法与传统的Bagging、Adaboost以及将KELM作为基分类器的Bagging_KELM［21］作对比，基于D-A-WHA测度的选择性集成算法的权重ε在Breast、Lung和Ovarian数据集中分别取1、1．7和1．5。实验结果如图3所示，可以看出D-A-WHA选择性集成的分类精度明显比其他算法高。

图3 不同数据集下各算法分类精度Fig．3 Accuracy of each algorithm on different datasets

4．3 实验分析

表3是不同集成学习算法取10个基分类器集成时精度、均方差和运行时间的实验结果对比，可以看出相对于其他几种算法，D-A-WHA算法不仅分类器精度最高，而且均方差更小，也就是更稳定。同时比传统的的Bagging和Adaboost运行更快，与Bagging_KELM相比运行速度相对较慢，但在精度和算法的稳定性方面，D-A-WHA算法要优于Bagging_KELM。

表3 不同算法的精度、均方差和运行时间对比Tab．3 Comparison of different algorithms in accuracy，mean square error and running time

5 结语

机器学习在生物信息学的研究中已经越来越受到重视，但基于基因表达数据的癌症分类仍是一个具有挑战性的任务［22］。本文提出一种基于D-A-WHA选择性度量的基因表数据选择性集成算法，针对传统的选择性集成学习算法难以平衡基分类器之间的差异性和准确性的问题，同时考虑基分类器之间的差异性和准确性选择部分基分类器进行集成。通过在癌症基因表达数据集上的分析，该算法在精度、稳定性和运行速度方面都优于传统的集成学习算法。但是对于如何更好地自动寻找D-A-WHA的最优权重ε还无法确定，因此如何在不同数据集下自动选择D-A-WHA的最优权重ε将是我们下一步的研究方向。