岩石薄片图像拼接中的色差校正算法

袁 媛，滕奇志，何小海，张余强

(1.四川大学 电子信息学院 图像信息研究所，四川 成都 610065;2.成都西图科技有限公司，四川 成都 610065)

0 引 言

在石油地质勘探行业中，通常使用采集到的岩石样本制成的岩石薄片研究地质油气分布情况。由于岩石薄片在长期保存中容易受到损坏，而图像资料能够完整持久地保存岩石薄片信息，因此利用相机来采集显微镜放大的岩石薄片图像，对于后续岩石薄片的研究和保存具有重要的意义。在显微镜下拍摄岩石薄片时，通常只能拍摄到岩石薄片的局部视域图，为了构造整个岩石薄片图像，需要对其分区域逐行逐列进行序列图像采集，得到一系列具有部分重叠区域的岩石薄片序列图像，然后对岩石薄片序列图像进行图像拼接，进而构造成一幅具有高分辨率的岩石全薄片图像。然而，在连续采集过程中，由于拍摄环境(如光线)、岩石薄片自身性能(如薄片厚度、损坏程度)等原因，会导致岩石序列图像之间往往存在亮度和色彩差异，从而导致拼出的结果图有明显的“块”效应，不能准确地保留完整的岩石薄片信息。

目前常用的图像拼接算法中，主要针对拼接缝区域进行颜色校正[1-3]，而对于两幅图像之间本身就有的颜色差异，只校正拼接缝区域并不能完整地改善拼接结果图质量。而针对两幅完整的光照不均匀、色彩不一致的图像，已有一些校正算法。例如，李勇等[4-5]基于直方图匹配的图像匀光算法，根据模板直方图与目标直方图累计归一化数据进行直方图匹配处理，实现对图像亮度的校正，但该方法在图像直方图差异较大时，会改变原有图像灰度级的相对距离。李德仁等[6]提出基于Mask原理的匀色算法，其需要高斯滤波器模拟图像的亮度分布作为背景图像，通过原始图像减去不均匀背景图像达到匀色目的，但这种方法主要针对灰度图像，对彩色图像匀色效果不好。吕楠等[7]提出了一种多相机图像拼接匀色算法，但其只针对拍摄一行图像进行处理，不适用于岩石薄片多行多列的全薄片图像拼接。

在已有算法的基础上，文中通过将岩石序列彩色图像从RGB颜色空间转换到lαβ颜色空间，然后利用Wallis滤波器分别计算两幅图像重叠区域l,α,β各个空间的均值和方差，校正目标图像的色彩亮度，再按照类“王”字型顺序整体调整序列图像的光照和色彩。

1 算法理论基础

1.1 颜色空间的选择

lαβ颜色空间是基于人眼的视觉感知，由亮度分量l,色度分量α、β组成，其中α分量表示黄-蓝通道，β分量表示红-绿通道。lαβ颜色空间的各个通道之间相关性较弱，有利于后续分通道进行亮度色差计算。因此，将彩色图像从RGB颜色空间转换到lαβ颜色空间进行处理。lαβ空间是从LMS空间转换过来的，LMS空间是基于人眼视网膜上对短波光线敏感的锥体细胞(S锥体)，对中波光线敏感的锥体(M锥体)，对长波光线敏感的锥体(L锥体)的颜色空间。因此要将颜色值从基于设备的RGB空间变换到lαβ空间，先要将颜色值转化到基于对波长敏感的LMS空间。

(1)先将RGB空间转换到LMS空间。

(1)

(2)由于LMS空间的分量分布比较分散，为了使其聚敛，将其转换到LMS对数空间。

L'=lgL

(2)

M'=lgM

(3)

S'=lgS

(4)

(3)将LMS对数空间转换到lαβ空间。

(5)

在lαβ空间进行图像色差校正后，为了后续进行图像融合，需要将校正结果图像从lαβ空间变换回RGB空间，其转换步骤如下所示：

(1)将lαβ空间转换到LMS对数空间。

(6)

(2)从LMS对数空间转换到LMS空间。

L=10L'

(7)

M=10M'

(8)

S=10S'

(9)

(3)从LMS空间转换到RGB空间。

(10)

1.2 Wallis滤波器特性

Wallis滤波器是一种应用于图像增强的滤波器[8]。它可以增强原始图像的反差，同时抑制噪声，其目的是将图像局部的灰度均值和方差(即图像灰度动态范围)映射到给定的灰度均值和方差。它是一种局部图像变换，使得在图像不同位置处的灰度方差和灰度均值具有近似相等的数值。一幅图像l分量的均值反映其亮度，在α、β分量的均值反映其在该分量的色调统计量，而标准差则反映了该分量的灰度动态范围。由于相机采集全薄片过程是连续的，因此在理想情况下获取的序列图像在色彩空间上也应该是连续的，具有近似一致的色调、亮度和反差，即也应该具有近似一致的均值和标准差。因此，文中主要采用Wallis滤波器进行两幅图像之间的匀光匀色处理。

Wallis滤波器的一般形式为：

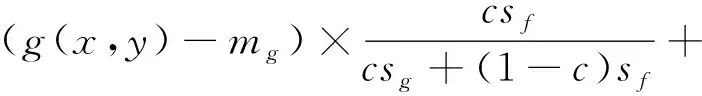
bmf+(1-b)mg

(11)

其中，g(x,y)为原始图像的灰度值；f(x,y)为目标图像的灰度值；mg为原始图像的局部灰度均值；sg为原始图像的局部灰度标准差；mf为目标图像的局部灰度均值；sf为目标图像的局部灰度标准差；c∈[0,1]为图像方差的扩展常数；b∈[0,1]为图像的亮度系数。

在式11中，当b趋向于1时，目标图像均值mf起主要作用；当b趋向于0时，原始图像均值mg起主要作用；当c=1,b=1时，为典型Wallis滤波器，如下：

(12)

其中，当mg=mf，sg=sf时，目标图像的均值和方差与原始图像的均值和方差相同，进行变换时不会改变图像的灰度值，适用于图像拼接时重叠区域的颜色校正[9]。

2 岩石薄片序列图像拼接

2.1 图像配准

由于岩石薄片颜色、亮度等信息差异较大，文中主要采用SIFT(scale-invariant feature transform)算法进行配准。SIFT算法[10]主要是通过在尺度空间寻找极值点，提取位置、尺度、旋转不变特征量等信息，形成128维特征描述符。对所有待拼接的序列图像采用SIFT算法查找其特征点，然后利用特征描述符的欧氏距离作为两幅图像的特征点的相似性判定度量。取其中一幅图像的某个特征点，找出相邻图像中与其距离最近的前两个特征点，对于这两个特征点，若最近距离除以次近距离小于某个阈值时，则可以接受该匹配点[11]。

在实现图像之间的粗匹配后，利用RANSAC模型进行参数估计[12]，剔除“误匹配”点，得到图像间的单应矩阵H。

2.2 图像色差校正

2.2.1 两幅图像色差校正

(1)颜色空间转换。

由于lαβ颜色空间各个通道相关性较弱，有利于后续匀光匀色分通道进行参数校正，因此首先将参考图像和目标图像进行颜色空间转换，即将图像从RGB颜色空间转换到lαβ颜色空间，转换公式如式1～5。

(2)重叠区参数计算。

根据单应矩阵H获得两幅图像间的重叠区域A(x,y)、B(x,y)，其尺寸大小均为m×n，将参考图像1重叠区域的lαβ通道分解成l1、α1、β1，目标图像2的重叠区域的lαβ通道分解成l2、α2、β2，分别计算两幅图像重叠区域各个颜色分量的灰度均值m1、m2和灰度标准差s1、s2。

(13)

(14)

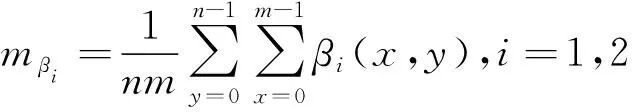
(15)

(16)

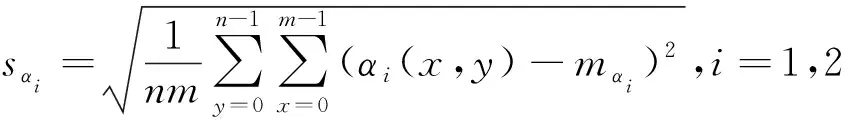
(17)

(18)

其中，ml1、mα1、mβ1表示参考图像1在lαβ空间各个通道重叠区域的均值；ml2、mα2、mβ2表示目标图像2在lαβ空间各个通道重叠区域的均值；sl1、sα1、sβ1表示参考图像1在lαβ空间各个通道重叠区域的方差；sl2、sα2、sβ2表示目标图像2在lαβ空间各个通道重叠区域的方差。

(3)图像匀光匀色。

由于这是两幅图像的重叠区域，所以理论上二者在lαβ空间的均值和方差应该基本一致，但是由于实际拍摄过程中拍摄环境和岩石薄片自身性能等因素，导致两幅图像重叠区域得到的均值和方差差别较大。采用Wallis滤波器，将参考图像1的颜色信息迁移至目标图像2，使两幅图像间的色彩亮度趋于一致。利用式12，对目标图像2中的每个通道的每个像素点使用Wallis滤波器，如下所示：

(19)

(20)

(21)

得到新的l,α,β分量后，将lαβ三个通道合并，再利用式10将目标图像从lαβ颜色空间转换到RGB颜色空间显示，即可得到与参考图像1亮度色彩一致的新的图像2。

2.2.2 序列图像色差校正

岩石全薄片图像是由采集多行多列的序列图像拼接而成，其采集顺序类似于“S”型。首先，采集系统在x方向上横向移动薄片，y坐标保持不变，在到达一行的末尾时，直接在y方向上进行平移，x方向坐标保持不变，接着向y的负坐标方向移动，依次循环，直至采集完全薄片视域。

常用的颜色校正算法通常只是平行地拍摄自然景物或灰度图像，并且对一行图像进行处理，在初始参考图像的选择上，有的采用分块影像中光照充足且分布均匀、具有最高亮度均值的图像作为初始参考图像进行颜色校正[13]，有的先计算图像的信息熵，选择信息熵最大的图像作为初始参考图像进行颜色校正[7]。当采用这些算法对岩石序列图像进行校正时，无法保证行与行之间的亮度信息趋于一致，会出现明显的一行一行的“裂痕”。

这种拼接结果图的视觉效果极差，只能保证一行图像的亮度一致，多行多列时会出现明显的“裂痕”，不利于保存真实的岩石薄片信息。而出现这种情况的原因常常是初始参考图像的选择只考虑了单行图像，然后按顺序依次调整，对于岩石薄片这种由多行多列序列图像组成的拼接结果图像而言，还需要考虑行与行之间色彩亮度的差异性。针对这种情况，采用类“王”字型顺序对全薄片进行亮度及色彩调整，如图1所示。

图1 类“王”字型顺序色彩亮度调整

其中，一条线代表一行图像，竖线代表了列中心，中间的圆代表了整幅薄片的中心图像。

(1)对所有序列图像先查找SIFT特征点，然后进行图像配准，得到序列图像两两之间的单应矩阵H，确定图像之间的重叠区域。

(2)找到在全薄片显示最中心的图像，并对其作自动白平衡，作为初始参考图像R(x,y)。

(3)对R(x,y)所在列按2.2.1所述方法进行图像色差校正，保证初始参考图像R(x,y)所在列的图像色彩亮度趋于一致，然后将校正后的图像作为该行的次级参考图像SRi(x,y)。

(4)对于第i行图像，以次级参考图像SRi(x,y)作为参考图像，依次向两侧分别用2.2.1所述方法逐个进行图像色差校正，整个图像颜色校正顺序类“王”字型展开。

(5)所有序列图像完成色差校正后，再计算各个图像相对于参考图像的单应矩阵，然后进行多分辨率图像融合[14-15]，最终得到一幅图像色彩亮度一致的高分辨率拼接结果图。

3 实验结果与分析

拍摄的相机采用Canon EOS 600D，通过偏光显微采集系统拍摄了多组岩石地质薄片进行实验，其中多组图像都出现了亮度色彩不一致的情况。先采用基于Wallis滤波器的颜色校正算法试验两幅图像校正后进行拼接的效果，再采用类“王”字调整顺序的颜色校正算法试验多行多列序列图像拼接后的效果。

3.1 两幅图像色差校正

图2是由相机连续拍摄的两幅相邻图像，其拍摄参数固定为曝光时间1/20 s，ISO为800，光圈值为F/5。

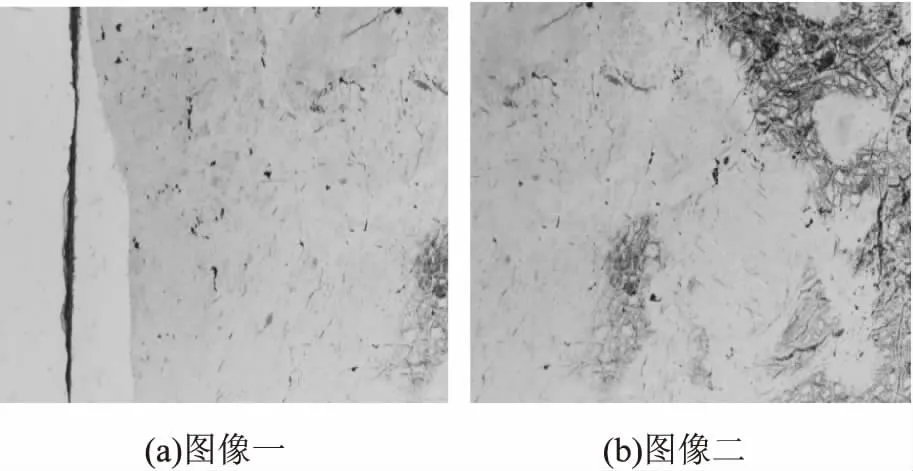
图2 相机连续拍摄图像

观察图2可以发现，两幅图像有重叠区域，并且重叠区域图像的亮度、色彩都不一致，如果直接采用图像拼接算法，未对图2(a)进行色差校正，得到的拼接结果见图3。

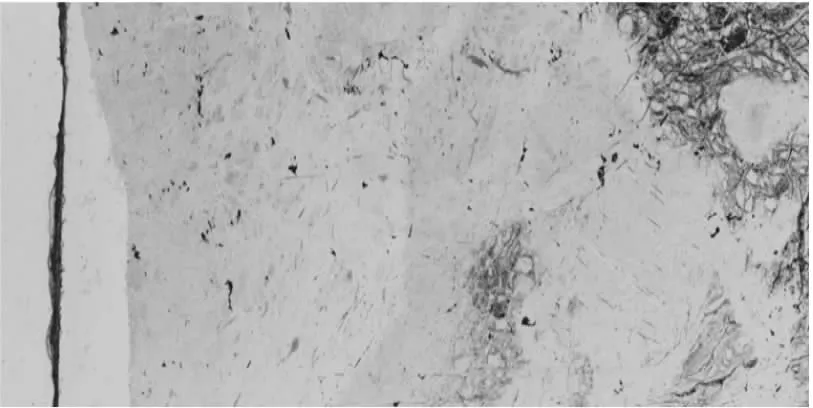
图3 两幅相邻图像拼接结果

观察图3可以发现，虽然两幅图像的拍摄固定参数一致，但是两幅图像的色彩亮度存在明显的差异，即便在图像融合算法中使用了多分辨率融合，但是直接拼接后，拼接结果图仍然有明显的拼接缝并且图像色彩亮度不一致，不利于保存岩石薄片信息。

采用文中的颜色校正算法，将图2(b)作为参考图像，图2(a)作为目标图像，进行颜色校正处理后得到新的图像。然后再对两幅图像进行拼接，拼接结果如图4所示。

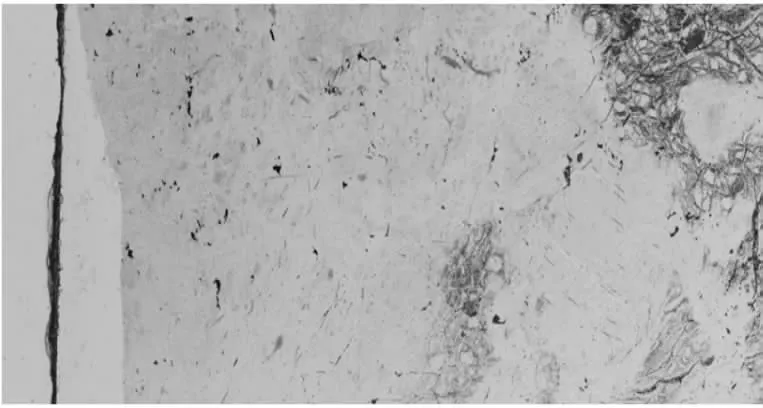
图4 处理后的拼接结果

对比图3和图4可以发现，采用文中算法能明显地改善岩石序列图像色彩亮度不一致的问题。

3.2 序列图像拼接

两幅图像色彩亮度调整是序列图像调整的基础。由相机连续拍摄24张序列图像，图2(a)、(b)是序列图像中的两幅图像。其未进行色差校正直接拼接的结果如图5(a)所示。可以看出该图中间区域由于相机白平衡效果不同，其色彩与周围区域出现明显差别，在这种情况下，只处理拼接缝的亮度色彩差异不能改善结果图的整体效果。采用文中所述的类“王”字型序列图像色差校正算法，以最中心图像作为初始参考图像进行处理，得到校正色彩后新的序列图像，用新的序列图像进行图像拼接后的结果如图5(b)所示。

图5 拼接图像

4 结束语

提出了一种针对色彩亮度不均匀岩石薄片序列图像的拼接算法。将待拼接图像先转换到lαβ色彩空间，然后利用SIFT算法进行图像配准后获得图像间重叠区域，计算重叠区域的Wallis滤波器相关参数，然后对目标图像的色彩亮度进行调整。全薄片采用类“王”字型顺序进行色彩亮度调整。实验结果表明，该算法对于相机连续拍摄的色彩亮度不一致的岩石薄片序列图像有较好的改善，可以明显消除拼接结果图中因为色差出现的“块”效应。