基于脑电信号的癫痫疾病智能诊断与研究

柳长源 张付浩 韦琦

摘 要：针对医疗诊断中癫痫脑电信号分类准确率低、分类类别少的问题，依据粒子群算法和支持向量机理论，提出了一种基于粒子群算法优化支持向量机参数的信号分类检测技术。首先利用小波分析对脑电信号进行5层分解与重构，然后提取含有癫痫特征频率的3、4、5层重构信号的波动系数和近似熵等特征，计算不同状态不同尺度的脑电信号能量，根据不同状态不同尺度的能量分布，调整特征向量的系数。最后使用粒子群算法优化的支持向量机对脑电信号进行分类。实验结果表明，本文提出的方法可以正确识别健康、癫痫发作间期、癫痫发作期3种类型脑电信号，最终的识别率可以达到99.83%。

关键词：

癫痫脑电信号；波动系数；近似熵；粒子群算法；支持向量机

DOI：10.15938/j.jhust.2018.03.016

中图分类号： TP391.4；R318.04

文献标志码： A

文章编号： 1007-2683（2018）03-0091-08

Intelligent Diagnosis and Research of Epileptic Diseases Based on EEG Signals

LIU Chang-yuan， ZHANG Fu-hao， WEI Qi

（School of Electrical and Electronic Engineering， Harbin University of Science and Technology， Harbin 150080，China）

Abstract：Aiming at the problem of low accuracy and classification of epileptic EEG in medical diagnosis，a signal classification and detection technique based on particle swarm optimization （PSO） was proposed to optimize the support vector machine （SVM） based on the theory of particle swarm optimization and support vector machine （SVM）.Firstly， the EEG signals were decomposed and reconstructed by wavelet analysis.Secondly， the coefficients of fluctuation and approximate entropy of the reconstructed signals containing the functional parameters of epilepsy were extracted. Finally， The support vector machine （SVM） optimized by particle swarm optimization （PSO） is used to classify the EEG signals. The experimental results show that the this method can correctly identify three types of EEG signals in healthy， interictal epilepsy and epileptic seizures， the final recognition rate can reach 99.83%.

Keywords：epileptic EEG signals；coefficient of fluctuation； approximate entropy；particle swarm optimization； support vector machine

0 引 言

癲痫是一种以脑内神经元异常放电为特征的部分或全脑功能障碍的慢性病，我国拥有数量庞大的癫痫患者，且每年以60万例的速度在增加[1]。癫痫脑电信号分类与检测技术有助于减少医务工作者的工作量，具有实际意义临床应用[2]。袁琦等用近似熵、波动系数、极端学习机对癫痫脑电信号进行二分类，将脑电信号诊断为正常和癫痫发作期状态，识别率为98%[3]。庞春颖等根据改进的经验模式分解和支持向量机，对正常脑电信号和癫痫脑电信号进行分类，识别率为94% [4]。张涛等利用小波包分解系数矩阵、小波包熵、AdaBoost算法，将脑电信号分类成正常状态和癫痫发作状态，最终识别率为97.5%[6-7]。孟庆芳等用支持向量机和递归定量分析分类脑电信号，识别率为96% [5]。王杰等用样本熵、AR参数和自适应极限学习机对脑电信号进行分类，分类准确率为97.16%[8]。Lee Y等用小波变换和高阶矩相结合的方法提取特征，使用支持向量机对脑电信号进行分类，最终的识别率达到94.5%[9]。上述文献将脑电信号分类成正常状态和癫痫状态，但没有考虑癫痫发作间歇期信号的分类。本文提出一种粒子群算法优化支持向量机的信号分类检测技术，在保证分类精度的基础上，脑电信号被分类为正常状态，癫痫间歇期状态，癫痫发作状态。

1 实验数据与预处理

1.1 实验数据

本文使用的数据来源于德国波恩癫痫研究院癫痫脑电数据库，（文件下载网址http：//epileptologie-bonn.de/cms/front_content.php），该研究院脑电数据已广泛应用于癫痫脑电的分类与检测中[10]。实验数据统计如表1，该数据库分为5个数据集，数据集A、B是健康人在睁眼和闭眼时采集到的数据；数据集C、D是在致痫灶外和致痫灶区收集的数据，数据集E是癫痫患者癫痫发作时获得的数据。

1.2 脑电信号预处理

本文主要对正常、癫痫发作间歇期、癫痫发作期的脑电信号进行分类与检测，使用数据集A、数据集D、数据集E进行后续的实验。每个数据集包括100段脑电信号，每段时长23.6s，每段信号采集4097点，采样频率为173.6Hz。由Nyquist采样定理[11-13]，我们可以得出如下结论，癫痫脑电信号最高频率为80Hz左右，经研究表明，癫痫脑电波异常频率主要分布在0.5～35Hz之间，因此首先利用小波变换，对脑电信号进行分解与重构，提取出有效频段，然后求解特征向量。本文利用db4小波对实验数据集A、实验数据集D、实验数据集E进行5层小波分解重构，其中第3、4、5层重构信号频率主要集中在癫痫特征频段[15]。因此本次实验中，提取第3、4、5层重构信号的特征构建特征向量。

2 特征提取

由上节论述得知，本文要提取小波分解与重构后的第3、4、5层的脑电信号特征。根据脑电图（electroencephalograph， EEG） 在癫痫发作时，时频域的变化和时间复杂度的不同，本文提取波动系数，近似熵等特征表征癫痫脑电信号。

2.1 改进近似熵算法

近似熵算法（approximate entropy，ApEn） 能较好的反映信号序列的时间复杂性，是对产生一个新的模式的信号的概率的定量描述。序列越复杂，则近似熵越大，反之则越小。近似熵具有很强的抗干扰能力，可用近似熵作为特征提取平稳信号和随机信号。

对待处理的N个数据点的癫痫脑电信号，通过改进的近似熵算法进行计算，ApEn的值与m，r的取值有关。本文取m=2，r=0.2*std（sig），std（sig）为信号sig的标准差：

1）计算N*N的距离矩阵D，D的第i行第j列元素记为dij，所有我们可知距离矩阵D为对称矩阵。

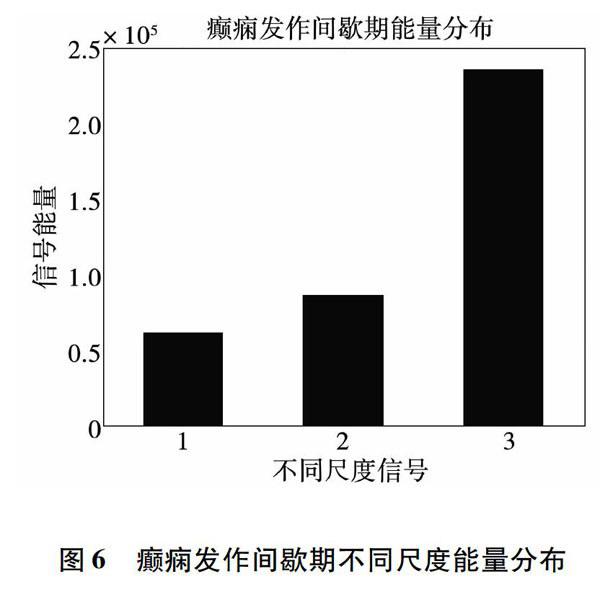
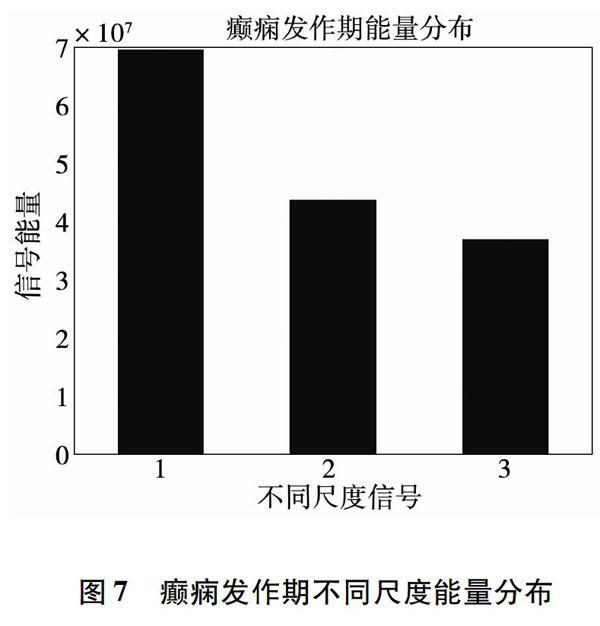
di，j=1， ui-uj

0，ui-uj≥r，i=1～N，j=1～N（1）

2）利用距离矩阵D中的元素，求得Cmi，Cm+1i：

Cmi=∑N-1j=1dij∩di+1j+1（2）

Cm+1i=∑N-2j=1dij∩di+1j+1∩di+2j+2（3）

3）根据Cmi，Cm+1i计算φmr和φm+1r

φmr=∑N-m+1i=1log（Cmi）/N-m+1（4）

φm+1r=∑N-m+1i=1log（Cm+1i）/N-m+1（5）

4）最后，根据φmr和φm+1r求得近似熵：

ApEnm，r =φmr-φm+1r（6）

由图1可见，健康状态、癫痫发作间期、癫痫发作期的近似熵的幅值具有较大差别，提取脑电信号的近似熵可以较好的表征不同脑电信号。

2.2 波动系数

经过长期的研究表明，癫痫发作时的脑电信号波动比正常时剧烈，不同状态的脑电信号波动系数有较大的差异，因此可以选择波动系数来衡量信号状态[9-10]，波动系数可以表示为：

Fin=∑M-1j=1anij+1-ani（j）（7）

式中：ani为第n段脑电数据小波变换后第i层的幅度；M为信号的长度。n取值范围1-100，i取值范围3、4、5，M取1024。

由图2、图3、图4可知，第三、第四、第五尺度的波动系数，在不同状态下有较为明显的差异。癫痫发作期波动系数最大而且波动性较强；癫痫发作间歇期的波动系数较为平稳，且值处于健康状态和癫痫发作状态中间；健康状态下的波动系数最为平稳且值最小。因此可用不同尺度下的波动系数作为脑电信号特征。

2.3 动态调整特征系数权重

本小节计算出不同状态、不同尺度EEG序列能量分布，以能量分布比例调整特征向量权重，能量分布高的频段所占比例大于1，能量分布低的频段所占比例小于1。

如图5、图6、图7所示，横轴表示第3、第4、第5尺度脑电信号，纵轴表示尺度信号的能量，不同状态的脑电信号在不同尺度下能量分布也有所差别。本文一个创新点是，计算不同状态不同尺度的脑电信号能量，根据不同状态不同尺度的能量分布，如表2所示，调整特征向量的系数，特征参数分配明细如表3所示。

不同状态、不同尺度下能量分布具体数值如表2所示。考虑到共3层信号，未设置系数时默认为1且各尺度系数之和为3，因此设定系数时以1为基准，某一尺度信号能量系数可以大于1，也可以小于1，但某一时期提取的特征，所有尺度信号能量系数之和等于3。由表2不同状态、不同尺度下能量分布的比例，调整特征向量的系数，特征向量权重分配如表3所示。

3 支持向量机分类器

支持向量机（support vector machine，SVM）廣泛应用于模式识别和分类检测中[13]，SVM很好的解决了高维度，小样本，非线性等问题。支持向量机的核心思想是，找到一种能够对两类样本进行正确分类的最优分类面，且不同样本距分类面距离越大，分类效果越好。

3.1 最优分类面

假设有两类待分类的实验数据：x1，y1，x2，y2，…，xn，yn，x∈Rn，yi∈1，-1（xi是实验数据，yi是实验数据的标签），存在一个最优分类面，其方程可以表示为：

wT·x+b=0（8）

通过这个最优分类面，可以分类两种类型的样本数据，我们令：

fx=wTx+b（9）

如果fx=0，那么x是位于分类面上的点；如果fx<0，可以设定x对应的标签y为-1；fx>0，那么x对应的标签y为1，至此就可以将实验数据进行分类。

如果所有测试样本都可以正确分类，测试样本应符合下列条件：

yiwT·xi+b-1≥0，i=1，…，n（10）

两条分类面H1、H2之间的距离是2/‖w‖，要寻找最优分类线，即使得2/‖w‖最大，也即12‖w‖2最小化，最优分类问题转化成一个约束优化问题

min‖w‖22（11）

s.t yiw.x+b-1≥0，i=1，…，N

求解上式的二次规划问题，得到最优分类面的w和b，最优分类函数为：

fx=sgnw·x+b（12）

图8中，正方形和圆形代表两种类型的数据，H代表最优分类面，H1、H2为各类中离分类线最近的样本且平行于分类面的直线，分布在该直线的点被称为支持向量，H1和H2的距离就是分类间隔。所谓最优分类面是指分类线既能正确分离两类，又能最大化分类间隔。wT是最优分类面的法向量，b为最优分类面的常数项。

3.2 核函数

对于线性不可分的数据，需要核函数对数据进行处理，在低维空间线性不可分的数据xi，通过非线性映射Φx到高维空间，使得数据在高维空間线性可分，在高维空间找出最优分类面。满足Mercer条件的核函数就可以实现非线性转换。

定义的Mercer条件的核函数：

Kxi，xj=Φxi.Φxj（13）

核函数有多种形式，经常使用的主要包含径向基函数、多项式函数、Sigmoid函数等。核函数的差异会构成不同的支持向量机，本实验选取的核函数是径向基函数。径向基核函数：

Kxi，xj=exp-‖x-xi‖2σ2（14）

3.3 SVM多分类算法

本文将脑电信号分为健康状态、癫痫发作间歇期状态、癫痫发作期状态，对脑电信号进行三分类。三分类问题可以理解为：给定属于3种类别的n个训练样本（x1，y1）， （x2，y2）…（xn，yn）yi∈0，1，2，通过上述训练样本构造分类器，将m个测试样本（a1，b1），（a2，b2）…（am，bm） bi∈0，1，2，进行三分类。

OAO（one-Agains-one decomposition）算法在每两类样本间训练一个分类器，对于K分类问题，有（K×（K-1））/2个分类器，当K取3时，则有3个分类器。用测试样本进行分类检测时，每个分类器都对其进行判断，并将识别出的诊断结果保存，最后统计分类结果最多的标签，即为分类结果。

4 粒子群算法优化支持向量机参数

支持向量机的惩罚因子C和核函数参数σ对数据分类具有很大的影响，这两个变量决定着支持向量机的泛化能力。如果得到最佳的分类效果，就要获取最佳的参数C和σ。一般来说这两个参数都是根据经验设定，无法获得最佳参数，也即无法获得最优分类率。本文利用粒子群（PSO）算法全局寻优的特点，对SVM的参数C和σ进行优化，寻找最优的参数值，进一步提高SVM学习能力和收敛速度[17]。

PSO算法是一种基于迭代寻优的算法，本文需要优化SVM的惩罚因子C和核函数参数σ，每个粒子可以想象成二维空间中的一点，PSO算法就是找到该二维空间中的最优位置，使得SVM对癫痫脑电信号的分类准确率最高。每个粒子在二维空间中的坐标表示为xi=xi1，xi2i=1，2，…，20，以速度vs=vs1，vs2s=1，2，…，20在二维解空间内进行搜索。粒子在更新位置时需要考虑粒子个体的最优位置pi和粒子种群最优位置pg。

pi=pi1，pi2，i=1，2，…，20（15）

pg=pg1，pg2，…pgn，n=20（16）

粒子根据式（17）、式（18）、式（19）更新飞行速度vs和位置。

vs+1=vs+c1rand1（）（pi-xi）+

c2rand2（）（pg-xi）（17）

xi+1=xi+vi+1（18）

vs=vmax，if vs>vmax

vs=-vmax，if vs<-vmax（19）

c1表示粒子向自身历史最优解靠近的权重因子，c2表示粒子向种群历史最优解靠近的权重因子，学习因子的值越大，粒子全局搜索能力越强。本文中c1取1.5，c2取1.7，rand1（）和rand2（）表示0到1的随机数。粒子种群数目设定为20，最大迭代数为200。

5 实验结果与分析

在本文中，脑电信号被分为三种不同的状态：健康期、癫痫发作间期、癫痫发作期。构造分类器时，将实验数据分为训练样本和测试样本，训练样本和测试样本见表4。训练样本：取50个数据集A的样本作为健康状态的数据；取50个数据集D的样本作为癫痫发作间歇期的数据；取50个数据集E的样本作为癫痫发作期的数据。将数据集A、数据集D、数据集E剩下的50个样本组为测试样本，利用测试样本对分类器性能进行检测。每一个样本信号采样4096个点，现将每段信号截取为4段，增加实验数据，提高实验的可靠性。

本文的两个创新点：一个是对提取的脑电特征增加了权系数；另一个是本文对脑电信号进行三分类，并利用PSO算法寻找支持向量机最佳参数，最后把脑电信号分成健康、癫痫发作间期、癫痫发作期不同状态，并可以提高分类准确率。现通过以下4个指标来对分类器性能进行判定。

1）准确率acc = 正确分类数量/测试样本数量

2）健康识别率p0 = 正常状态正确分类数量/正常状态的数量

3）间期识别率p1 = 间期状态正确分类数量/间期状态的数量

4）发作期识别率p2 = 发作期状态正确分类数量/发作期状态的数量

表5为本文三种实验结果对比，可以直观的看出：设置特征向量系数后，癫痫疾病诊断分类准确率有较大的提升，优化支持向量机后分类准确率进一步提升，但训练时间大幅增加，对于识别准确率与识别时间的矛盾需具体问题具体分析，若更看重识别效率则选择未优化支持向量机的方法，若更看重识别准确率则选择优化的支持向量机进行癫痫疾病的诊断

本文实验结果与其他方法的对比如表6所示，本文不僅将脑电信号分类为3种脑电信号，而且相比之前的准确率有所提高，解决了分类准确率和分类数的冲突。

6 结 语

国内外学者将现代数字信号处理技术应用到癫痫疾病诊断中，对脑电信号进行预处理、构建特征向量、识别分类，最终实现快速定位致痫区域。

本文汲取了其它文献的优点，弥补了癫痫智能诊断中分类类别少，分类准确度低的缺点，最终分类准确度达到99.83%，具备良好的实验效果。本文提取的特征维度较高，可能造成特征冗余，后期工作可在这方面做一些优化，进一步提高分类准确率。而且还可以做出操作界面，将各种实验方案整合在界面中，简化操作步骤，便捷地观察实验仿真结果，并对多个实验进行对比分析。

参 考 文 献：

[1] 张威，等.张京硕.癫痫300问[M].北京：化学工业出版社，2011：134-141.

[2] 郑效来，邱天爽，赵庚申，一种基于EEG特征提取的癫痫棘波综合检测判决方法[J].中国生物医学工程学报，2005，24（6）：696-699.

[3] 袁琦，周卫东，等.基于 ELM和近似熵的脑电信号检测方法[J].仪器仪表学报，2012，33（3）： 514 - 519.

[4] 庞春颖，王小甜，等.一种基于改进经验模态分解的癫痫脑电识别新方法[J].中国生物医学学报， 2013，32（6）：663-669.

[5] 孟庆芳，等.基于递归量化分析与支持向量机的癫痫脑电自动检测方法[J].物理学报， 2014， 63（5）：050506_1- 050506_8.

[6] 张涛，陈万忠，等.基于AdaBoost算法的癫痫脑电信号识别[J].物理学报，2015，64（12）：128701_1-128701 _ 7.

[7] 张涛，等. 基于频率切片小波变换和支持向量机的癫痫脑电信号自动检测[J].物理学报，2016， 65（3）： 038703_1-038703_7.

[8] 王杰，李牧潇，等. 改进的极限学习机在癫痫脑电分类中的应用[J].计算机仿真，2014，31 （6），343-346.

[9] LEE Y，WAHBA G，ACKERMAN S.Classification of Satellite Radiance Data by Multicategory Support Vector Machines[J].Journal of Atmospheric and Oceanic Technology，2004（21）：159-169.

[10]张鹏博，王雪，等.癫痫发作瞬态带宽特征自适应检测方法[J].仪器仪表学报，2016，37（6），1390-1397.

[11]ZHOU W，LIU Y， et al.Epileptic Seizure Detection Using Lacunarity and Bayesian Linear Discriminant Analysis in Intracranial EEG [J].IEEE Transactions on Biomedical Engineering，2013，60（12） ：3375-3381.

[12]宋立新，王玉静，等.基于Hilbert-Huang变换的心率变异信号分析[J].振动与冲击，2007，26（10），30-34，186.

[13]尹芳，郑亮，等.基于Adaboost的视频文本定位[J].哈尔滨理工大学学报.2017，22（1）：103-108

[14]王鹏，李珊珊，等.便携式脑电信号实时采集系统[J].哈尔滨理工大学学报.2016，21（1）：77-82.

[15]周卫东，赵建林，等.癫痫脑电信号识别算法及其应用 [D].济南：山东大学.2010，：37-38.

[16]PARVEZ M，PAUL M. Epileptic Seizure Detection by Exploiting Temporal Correlation of Electroencephalogram Signals[J]. Signal Processing， IET，2015，9 （ 6 ） ：467-475.

[17]SONG Y， CROWCROFT J， ZHANG J.Automatic Epileptic Seizure Detection in EEGs Based on Optimized Sample Entropy and Extreme Learning Machine [J].Journal of Neuroscience Methods，2012，210 （ 2 ） ：132-146.

[18]王广泽.改进粒子群算法在供应链库存控制中的应用[J]，哈尔滨理工大学学报.2016，21（5），90-95

[19]BAJAJ V. Classification of Seizure and Nonseizure EEG Signals Using Empirical Mode Decomposition[J]. IEEE Transactions on Information Technology in Biomedicine，2012，16（ 6） ： 1135-1142.