基于代理模型的汽车正撞安全性仿真优化∗

陈媛媛,郑 玲

(重庆大学汽车工程学院,机械传动国家重点实验室,重庆 400044)

前言

传统的汽车碰撞安全研究方法为实车试验法，但这种方法研究周期长，费用昂贵且对试验设备和人员的要求较高。随着计算机辅助分析技术的不断发展和碰撞理论的逐渐成熟，汽车碰撞过程的有限元仿真得到实现，极大地缩短了开发周期。然而对于汽车碰撞这种复杂且存在高度非线性的动力学过程，有限元仿真技术无法满足迭代优化的计算要求，因此将代理模型应用于汽车碰撞安全优化的方法得到发展。

1992年文献[1]中首次利用代理模型对结构的抗撞性能进行分析，随后文献[2]和文献[3]中将其应用到结构的抗撞性优化中。经过长期的发展和完善，多项式响应面模型、Kriging模型和径向基函数模型等多种代理模型方法在碰撞安全领域得到广泛应用。目前，如何构造高精度的代理模型来替代有限元模型进行优化已成为汽车碰撞安全性优化的重点。文献[4]中采用随机抽样、分层抽样和拉丁超立方抽样3种方法进行样本点的选取并建立代理模型，通过比较其预测误差平均值和方差发现，拉丁超立方抽样法优于另外两种方式。文献[5]中对多元二次(Multiquadric，MQ)径向基函数和高氏(Gaussian)径向基函数中形式参数c的选择进行了研究，结果发现模型的拟合精度仅在合适的c值范围内提高。文献[6]中将多项式响应面函数和径向基函数应用于汽车前端部件的抗撞性优化问题，拟合后发现通过方差分析后的二次多项式响应面函数可以很好地对结构的能量吸收进行预测，而MQ径向基函数对峰值加速度的预测能力更高，说明对于不同的拟合对象应该单独分析，并选择合适的代理模型。

针对多目标优化问题，传统的优化方法迭代计算的周期长，优化效率低，亟需一种快速的优化计算模型来替代。本文中结合代理模型技术和多目标优化算法，采用代理模型代替有限元模型，以某乘用车正面碰撞安全性为对象，对该车质量、B柱加速度峰值和前围板侵入量进行了优化。

1 汽车正撞有限元模型

图1为某乘用车有限元模型，它包含778个部件，约105万个单元，93万个节点，总质量为1.642t。利用该模型建立100%正面碰撞仿真计算模型，采用LS-DYNA求解计算。图2为座椅横梁加速度响应均值的试验结果与仿真对比。由图可见，曲线的变化趋势基本吻合，说明此碰撞模型是准确的，其计算结果可靠有效。

图1 整车有限元模型

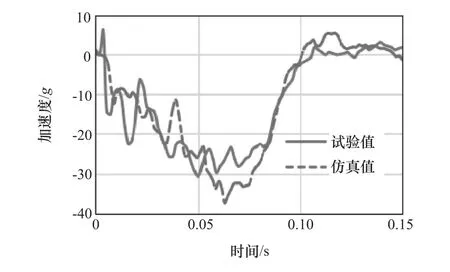
图2 座椅横梁加速度均值的试验结果与仿真对比

2 目标代理模型的建立

2.1 代理模型的基本方法

代理模型的建立包括以下两个方面：(1)采用试验设计方法，在变量空间中选取样本点的数量规模和分布位置；(2)利用数值模型(如有限元仿真模型)计算出各样本点处的输出响应值，得到代理模型可用的训练数据集，并在此基础上构建出相应的近似代理模型。

试验设计(design of experiment，DOE)是一种用来对多因素和响应变量关系进行处理和研究的科学方法[7]。目前常用的DOE方法有全因子试验设计、正交试验设计、拉丁超立方试验设计等，这里采用拉丁超立方试验设计方法。拉丁超立方试验设计是一种随机抽样法，具有“空间填充”的特征，可以保证整个变量空间都被样本点覆盖。

使用代理模型替代有限元模型时，首先需要保证代理模型的预测结果与有限元仿真计算结果足够接近，必须通过精度评估指标来提高代理模型在整个设计空间的响应预测能力。本文中利用检验样本点的平均相对误差作为模型的误差分析指标，其表达式为

RE的值越小越靠近0，说明模型的精度越高。

2.2 优化目标和设计变量

汽车碰撞过程是一种非常复杂的非线性动态过程，其响应是多种的，可被作为优化目标的变量也是多样的，如加速度、速度、力和位移等。汽车碰撞安全性优化的目的是，当汽车碰撞事故发生时，尽量保护乘员不受伤害或将受到的伤害程度降到最低，因此，作为优化的目标函数必须能表征乘员的安全状态或伤害程度。本文中以B柱加速度峰值和前围板侵入量最小化为优化目标，同时考虑轻量化的要求，将整车质量作为约束条件，三者的初始值分别为35.3g，138.54mm 和 1.642t。

在汽车碰撞过程中，主要的受力和吸能部件都在前端，因此选择碰撞过程中变形较大的前端板件作为优化的对象。将汽车前端12个板件厚度作为优化变量，根据结构的对称性，可简化为8个变量。表1为各板件的初始厚度和优化取值范围。

2.3 优化目标代理模型的建立

为研究样本数量对代理模型精度的影响，并得到相对明显的优化效果，采用拉丁超立方试验设计方法，共抽取了174组样本，用其中的150组数据作为训练样本集，剩余的24组数据作为检验样本点，并将其随机分为1和2两组检验样本，各12组数据，研究检验样本点变化对模型误差的影响。

2.3.1 测试点评价法构造代理模型

用150组训练样本集数据中不同数量的样本点分别建立各优化目标4种类型的代理模型，且每个代理模型的精度都用两组检验样本进行验证，得到模型预测值与仿真计算值之间的平均相对误差，作为模型精度的评价指标。图3～图5分别给出了两组不同检验样本点下各优化目标代理模型的误差变化曲线，图中SVD为二次多项式响应面模型，RBF_GS为高斯径向基函数模型，kriging为克里金模型，RBF_MQ为多元二次径向基函数模型。由于建立完全形式的二次多项式需要的最小样本数量为45组，因此多项式响应面模型的样本数量从45组开始变化，其余模型样本数量从30组开始变化。

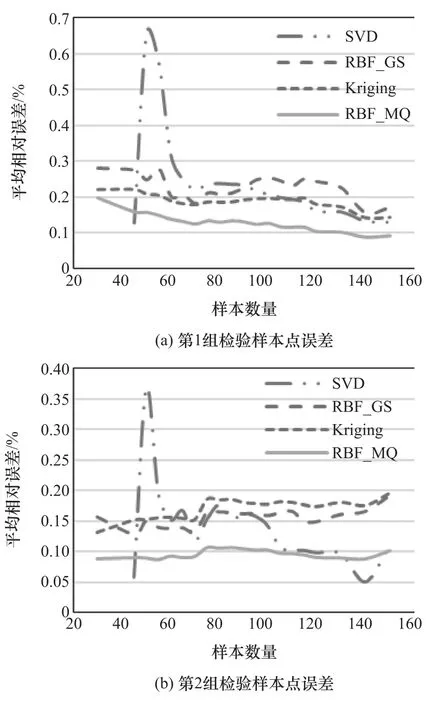
图3 整车质量的代理模型精度比较

从图中可以看出，在两组检验样本点下，当样本数量增加时，SVD模型的拟合精度变化最明显，拟合误差减小而精度提高，但波动也较大。与Kriging模型、RBF_GS模型和RBF_MQ模型相比，SVD模型的拟合精度较低，而当样本数量足够时，SVD模型也能达到较高的拟合精度。对Kriging模型和径向基函数模型而言，由于模型本身的拟合精度较高，样本数量的增加对模型精度的影响不大。这说明对于某些代理模型，即使增加样本点数量，也不能达到提高模型精度的目的，反而会花费大量计算时间。同时，由于整车质量的线性程度较高，各类型代理模型的拟合精度都较好，而对于B柱加速度峰值和前围板侵入量这种非线性程度较高的问题，代理模型的拟合误差都较大。

对比两组检验样本点下的模型误差，用两组样本点检验模型精度时，模型的误差有较大差别，说明采用测试点评价方法来对模型精度进行评估时，由于该方法是以检验样本点的平均相对误差作为评价指标，评价的结果在很大程度上取决于测试点的数目和位置，用随机产生的有限测试点可能很难对代理模型在整个设计空间的精度进行有效评价，导致出现较大的随机性和偏差。

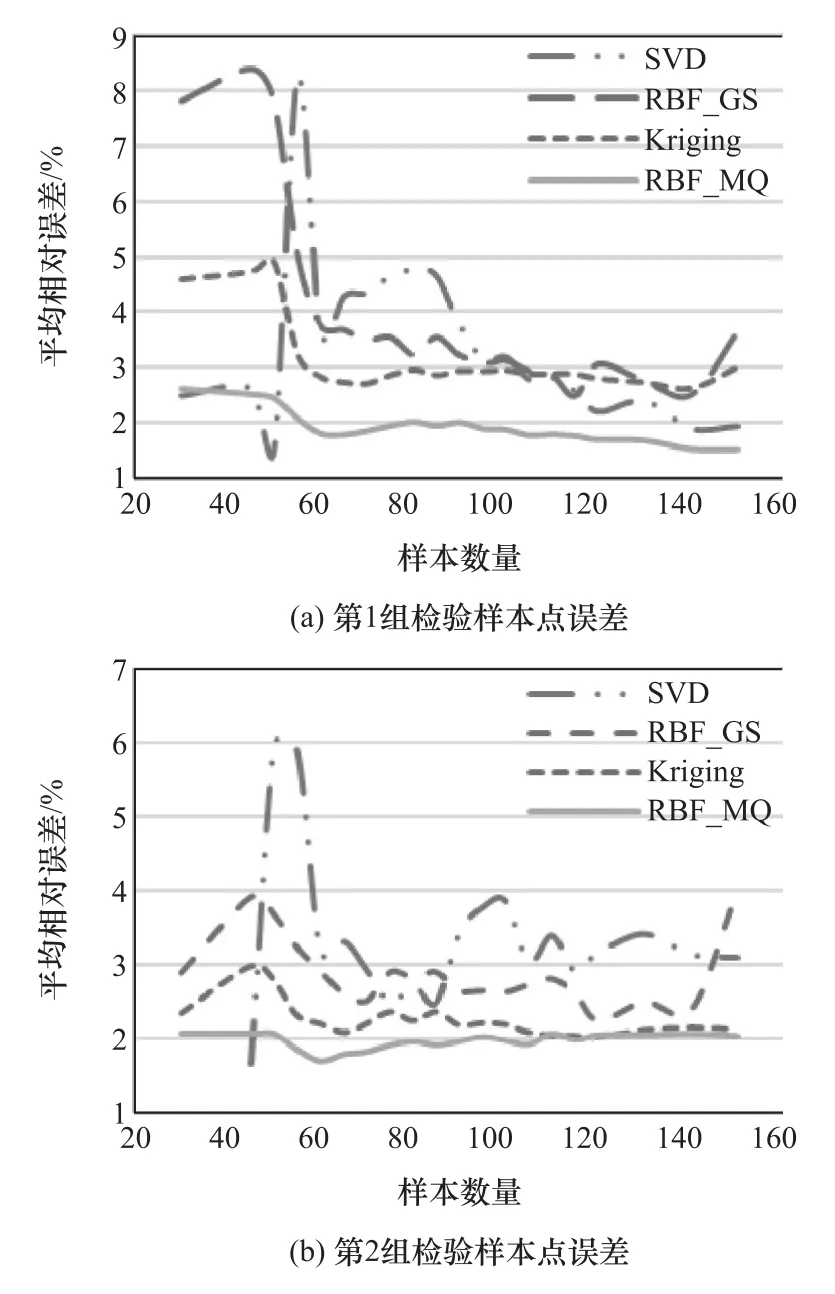
图4 B柱加速度峰值的代理模型精度比较

2.3.2 交叉验证法构造代理模型

交叉验证是一种简单的模型精度评价、模型选择方法，可以充分利用样本点信息对模型进行检验。其中，k-折交叉验证是最常用的方法，将样本集随机划分为大小相同的k份，其中k-1份作为训练集以构造子代理模型，剩下的1份作为验证集，然后依次轮换训练集和验证集，共进行k次子代理模型的构造和验证。将k次子代理模型的精度进行数据处理，通常采用求平均值的方法，得到整个模型的精度，而验证误差最小的模型即为所求模型。

本文中采用1次10折交叉验证法来对各优化目标的代理模型进行选择。将仿真计算得到的150个样本点随机划分为10组，每组15个，利用其中的9组构建子模型，则有135个样本点，剩下的15个样本点进行检验，如此进行10次。表2～表4分别给出了整车质量、B柱加速度峰值和前围板侵入量的不同类型代理模型的10组子模型的验证误差及其平均值，其中验证误差为检验样本点处预测值与仿真值的平均相对误差。

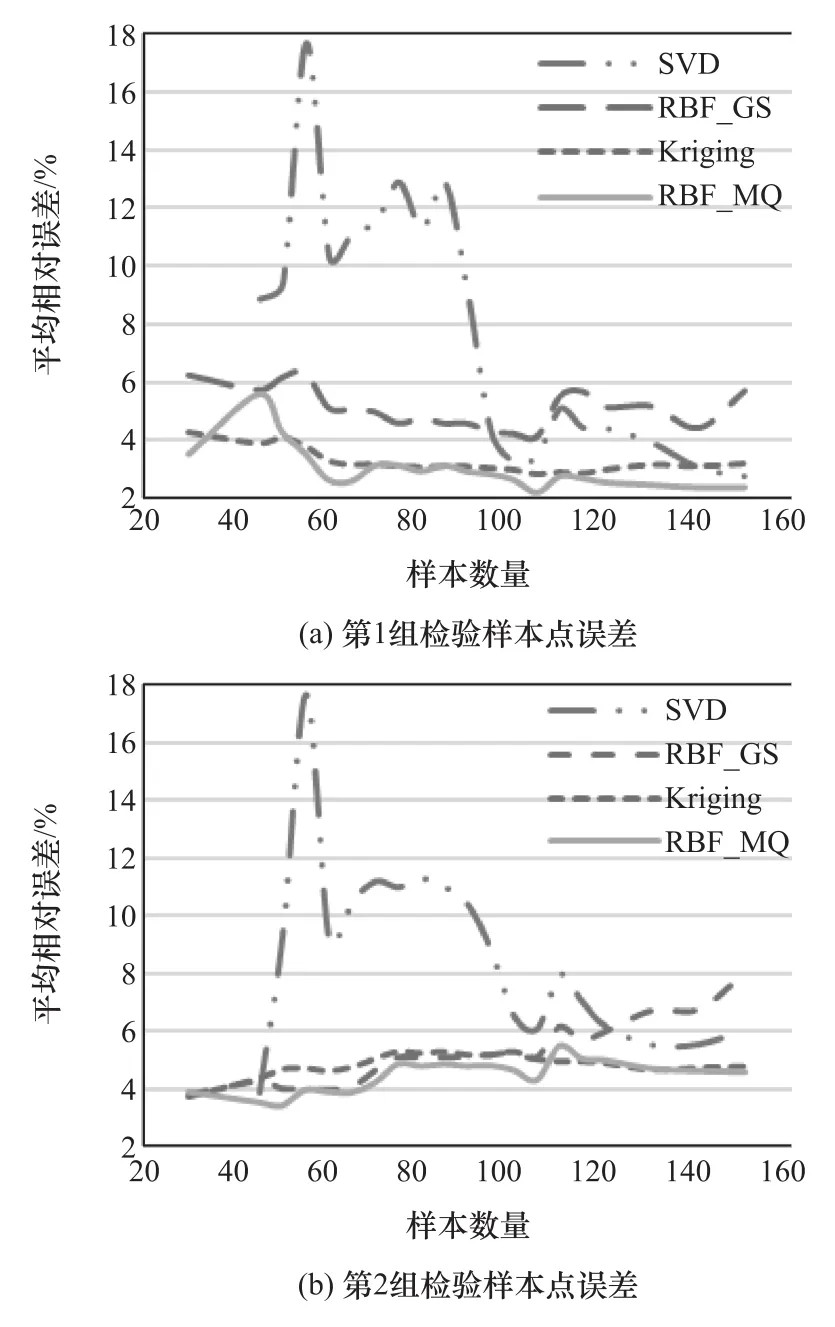
图5 前围板侵入量的代理模型精度比较

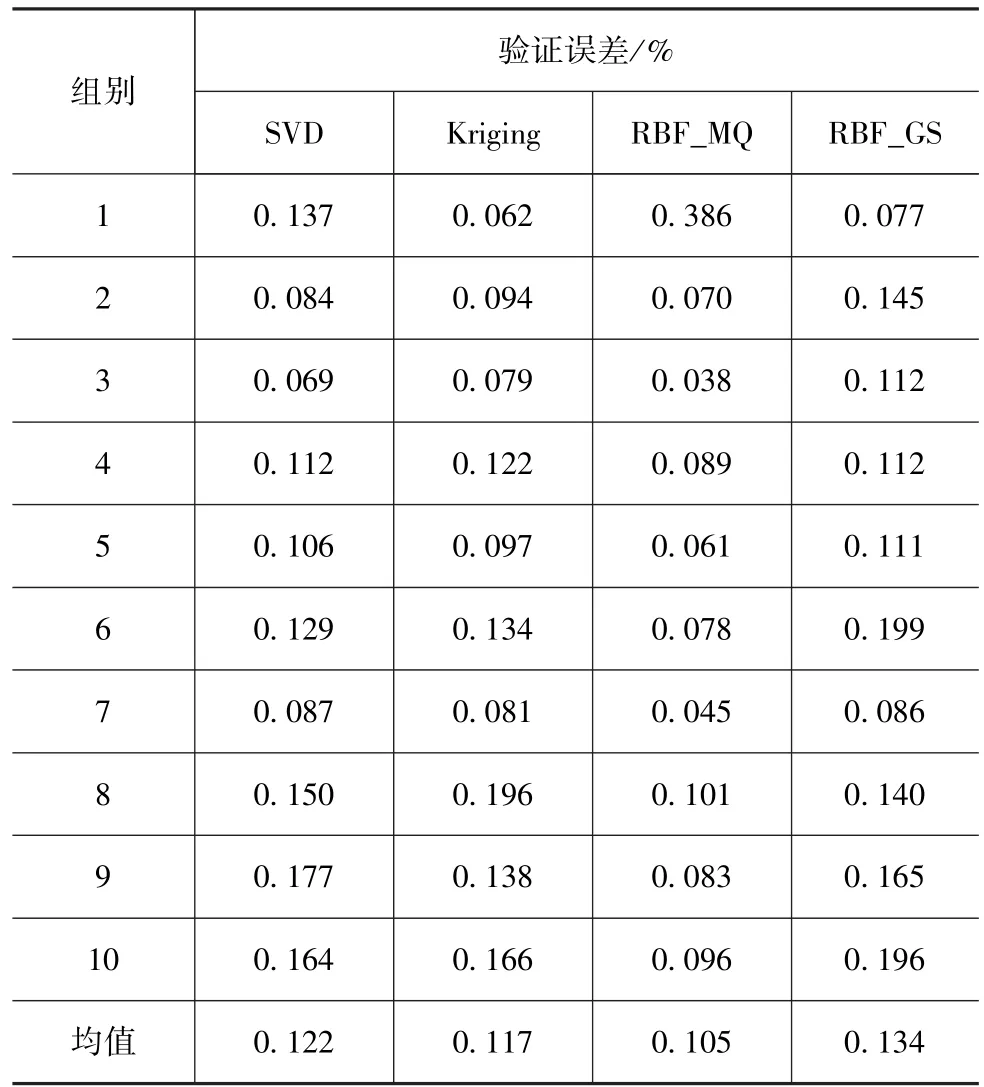
表2 整车质量子代理模型的交叉验证误差

从表2可以看出，在样本数量足够的条件下，对于整车质量这种非线性程度较低的问题，多项式响应面模型、Kriging模型和径向基函数模型均表现出较好的拟合效果，各子代理模型的验证误差都在0.2%以内，具有较高的精度，其中第3组RBF_MQ模型的验证误差最小，仅为0.038%。4种代理模型中，RBF_MQ模型的精度最高，Kriging模型其次，多项式响应面模型再次，而高斯径向基函数模型最差。

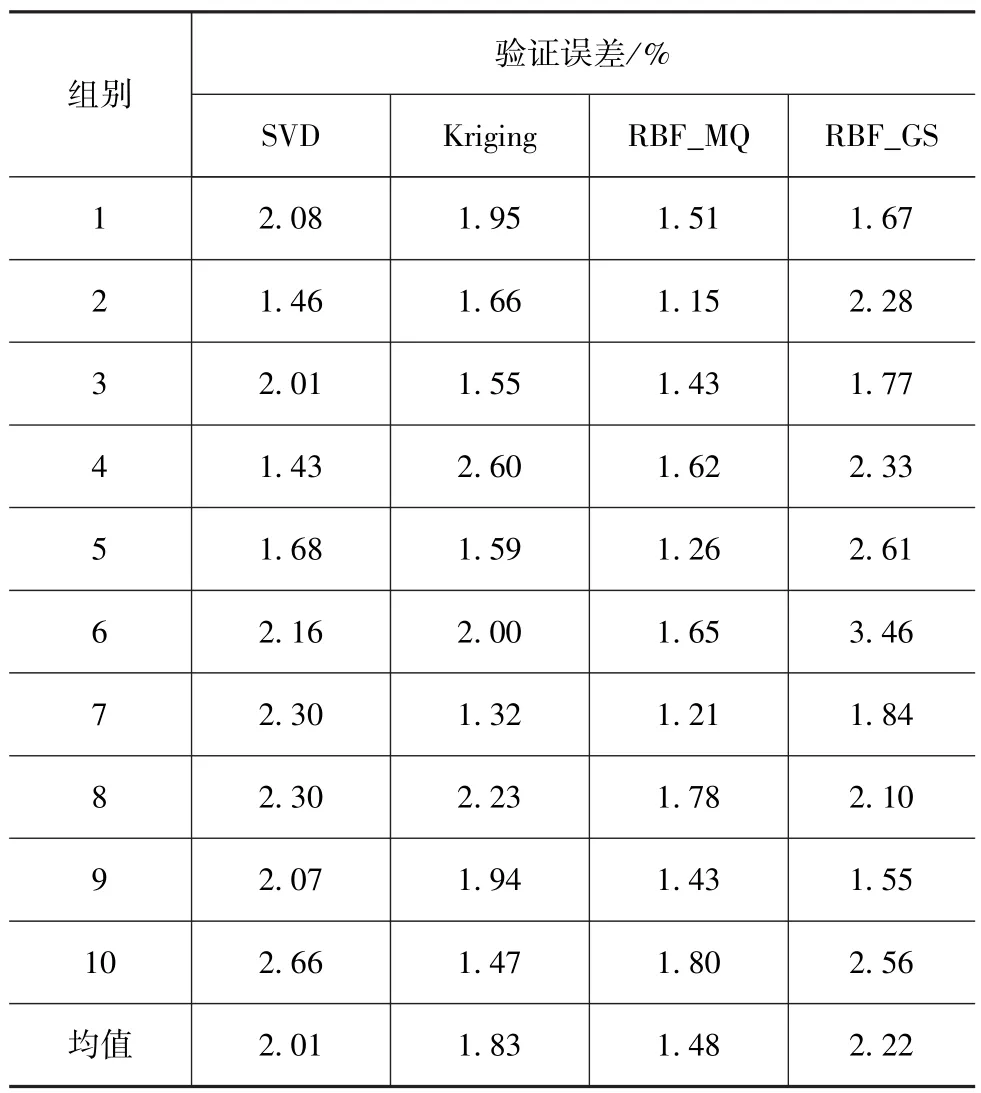
表3 B柱加速度峰值子代理模型的交叉验证误差

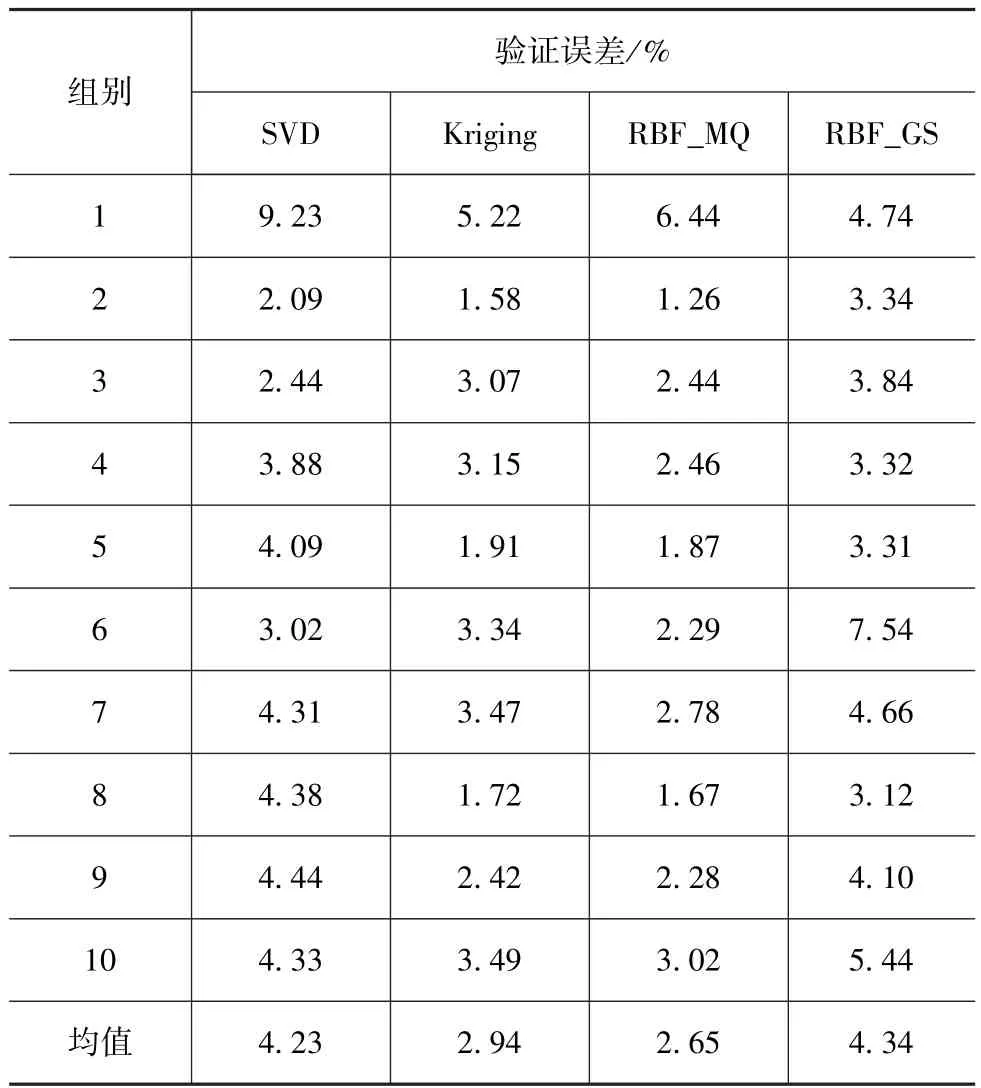
表4 前围板侵入量子代理模型的交叉验证误差

通过表3和表4可以看出，相比整车质量，B柱加速度峰值和前围板侵入量的非线性程度较高，代理模型的拟合精度相对较低，而前围板侵入量的非线性程度又高于B柱加速度峰值，误差更明显。B柱加速度峰值的子代理模型最大误差为3.46%，而前围板侵入量的子代理模型最大误差为9.23%，两个目标函数各子模型的最小误差也在1%以上。无论是B柱加速度峰值，还是前围板侵入量，拟合精度最高的子模型都是第2组RBF_MQ模型，误差分别为1.15%和1.26%；4种代理模型中，都是RBF_MQ模型精度最高，Kriging模型其次，多项式响应面模型再次，而RBF_GS模型最差。

综上所述，不论对于非线性程度较高，还是线性程度较高的问题，RBF_MQ模型和Kriging模型都表现出较优的拟合效果。其中RBF_MQ模型的精度更高，因此可优先选择。在样本数量充足时，多项式响应面对非线性问题的拟合精度也可达到要求，而高斯径向基函数模型的使用则可根据实际问题的需要和样本规模的大小进行选择。

3 正撞安全性多目标优化

3.1 优化目标代理模型的选择

表5给出采用两种模型评价方法时，3个优化目标代理模型的精度比较。可以看出，采用交叉验证方法构造的代理模型的最小误差更小，模型精度更高。因此，将表2中的第3组RBF_MQ模型、表3中的第2组RBF_MQ模型以及表4中的第2组RBF_MQ模型分别作为整车质量、B柱加速度峰值以及前围板侵入量的优化代理模型。

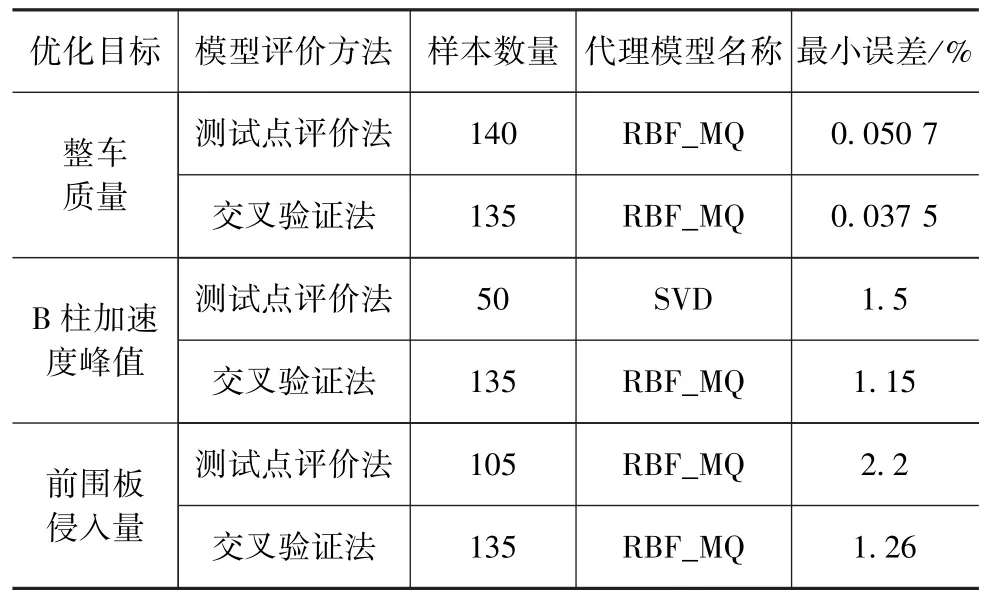
表5 两种评价方法的模型精度比较

3.2 多目标优化建模与求解

汽车正面碰撞安全性多目标优化的数学模型可表示为

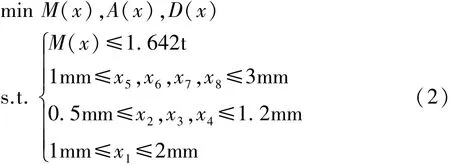
式中：M(x)为整车质量；A(x)为B柱加速度峰值；D(x)为前围板入侵量；x1～x8为待优化板件的厚度。

在Modefrontier软件中搭建优化流程，采用NSGA-II优化算法进行100次迭代寻优，得到176组Preto最优解。图6给出了Preto解集的气泡图。从图中可以看出：当整车质量处于较低水平时，B柱加速度峰值和前围板侵入量都处于较高水平，甚至超过了初始值，不符合优化设计的初衷；而当整车质量处于较高水平时，B柱加速度峰值虽然处于较低水平，前围板侵入量又显然偏大，不满足安全性的设计要求。出于对安全性和轻量化的考虑，首先满足对B柱加速度峰值和前围板侵入量的优化和降低程度，选择B柱加速度峰值和前围板侵入量都处于较低水平的Preto解作为最终的优化方案，如图中箭头所指。表6给出了该方案中各板件的厚度值和优化目标的优化解。

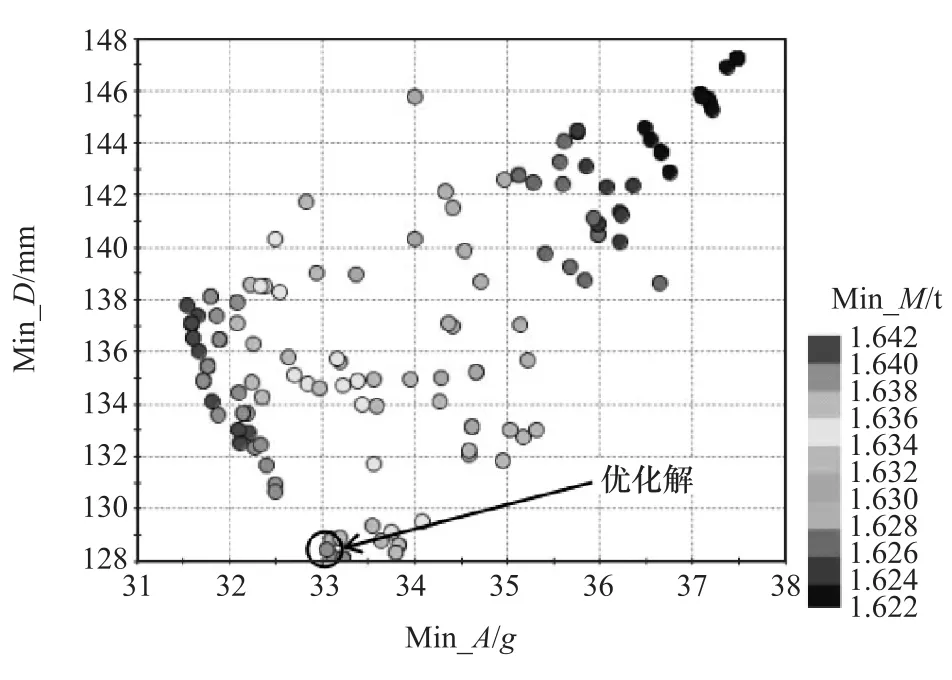
图6 优化目标的Preto解数值变化关系

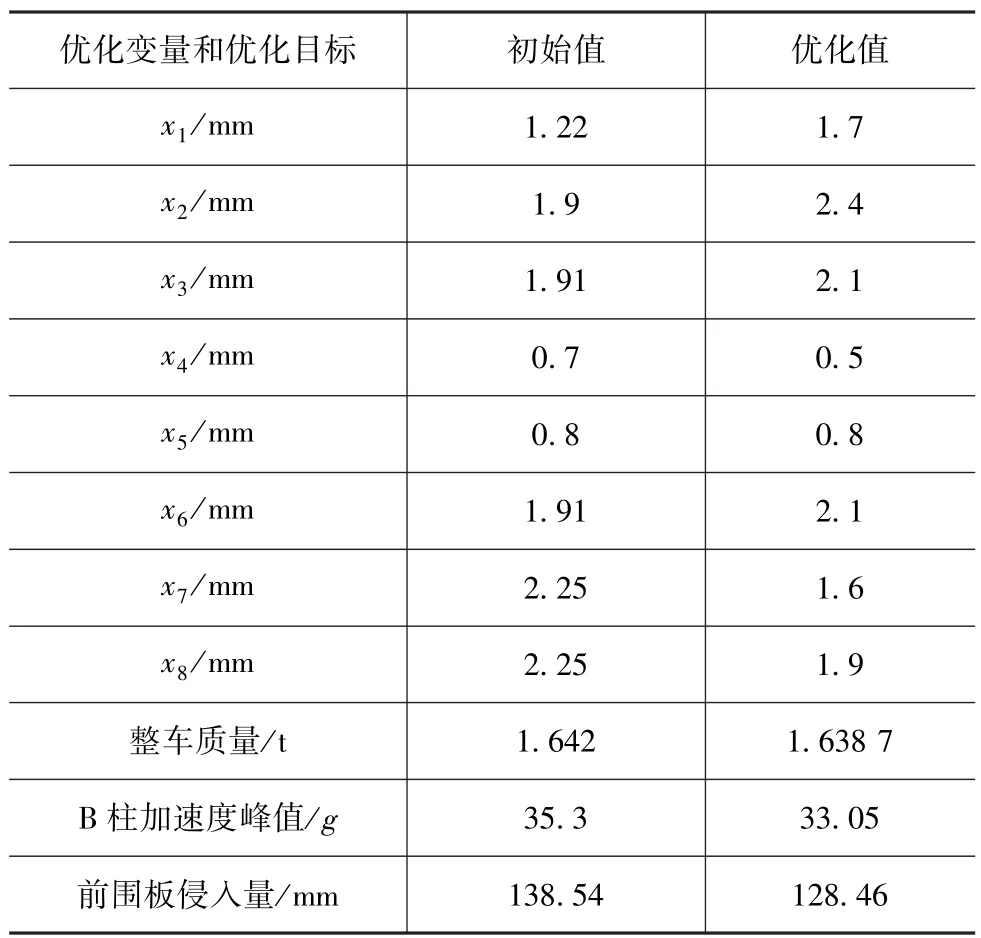
表6 多目标优化的初始值与优化值

代理模型的预测结果的准确性需要通过有限元计算来进行验证，表7给出了优化解的预测值与仿真值对比。3个优化目标的相对误差都在可接受的范围内，说明本文中构造的代理模型满足精度要求，可对仿真结果进行预测。优化后，整车质量为1.637 9t，减少了4.1kg；B柱加速度峰值为32.32g，比优化前降低了8.44%；前围板侵入量为130.19mm，比优化前降低了6.03%。

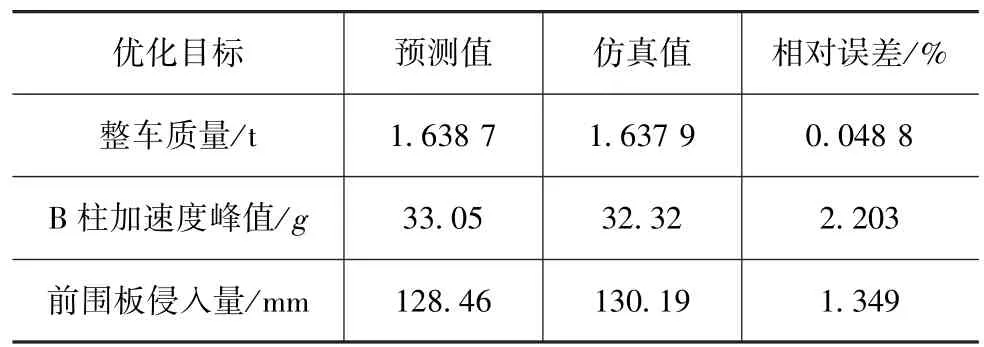
表7 优化解的预测值与仿真值对比

4 结论

结合有限元法和代理模型方法，对某乘用车100%正面碰撞安全性进行了优化，研究了样本数量对代理模型精度的影响，并比较了测试点评价方法和交叉验证法对模型精度评估的不同效果，得出结论如下。

(1)随着样本点数量的增加，代理模型的精度有提高的趋势，但当样本数量达到一定规模时，模型的精度不再随数量的增加而提高，此时扩大样本数量只会增加计算成本而达不到提高模型精度的目的。

(2)对于线性程度较高的问题，多项式响应面模型、Kriging模型和径向基函数模型都有较好的拟合效果；对于非线性程度较高的问题，宜采用MQ径向基函数模型和Kriging模型，若样本数量足够，多项式响应面模型也能达到较好的拟合效果。

(3)采用测试点评价方法对模型精度进行评估时，产生的结果在很大程度上取决于测试点的数目和位置，测试点不同，模型精度的评估结果可能会有较大的差异。由于测试点是有限的，如本文中只用了12个测试点来计算模型误差，因此使用随机选取的有限的测试点可能很难对代理模型在整个设计空间的精度进行有效评价，这种评价方法存在较大的随机性和偏差。而交叉验证法无需产生额外的检验点，通过充分利用现有样本点信息，可以确定出能对问题进行准确描述的主要成分，建立更高精度的替代模型。

(4)本文中的优化结果达到了碰撞安全性和整车轻量化的要求，且预测值与仿真值误差较小，说明构造的代理模型是准确的。说明将有限元法与代理模型技术相结合的方法可用于汽车碰撞的优化，对降低设计周期，提高工程优化设计效率具有重要意义。