多元逻辑代数理论及其在机械工程中的应用初探

朱永迪

（兰州职业技术学院，甘肃 兰州 730070）

逻辑代数也称为布尔代数，是分析和设计逻辑关系的一种数学工具，逻辑代数有“0”和“1”两种逻辑值，它们并不表示数量的大小，而表示逻辑两种状态，如开关的开与关等，所以逻辑代数中的“0”和“1”与自然数1和0有着本质区别[1]。若将逻辑代数两种状态推广到n种状态，对应的可用符号“0”、“1”、“2”、“3”、“4”、……、“n-1”来表示 n 种逻辑值，同理逻辑代数有“0”、“1”、“2”、“3”、“4”、……、“n-1”n 种逻辑值，它们并不表示数量的大小，而表示n种逻辑状态。传统的逻辑设计都是基于二值逻辑器件来处理逻辑问题的。然而，自然界多姿多彩的许多逻辑问题用二值逻辑是不易或不能解决的。在实际生产生活中，逻辑代数中“0”、和“1”两种逻辑值并不能完全满足应用要求。例如：机械控制中的“正转”、“停止”、“反转”三态，交通灯的红、黄、绿三种颜色等等，本身都属于三元逻辑问题。显然，研究多元逻辑代数在机械工程中的应用有着极其重要的意义。

1 多元逻辑代数的引入

多元逻辑代数同布尔代数一样，也是用字母表示变量。所不同的是，在布尔代数中逻辑变量的取值只有“0”、“1”、，多元逻辑代数根据实际生产生活应用可以定义n个值，n为有限值。0-1布尔代数逻辑变量为{0,1}，如引言中提到的机械控制中“正转”、“停止”、“反转”三态可用3元逻辑变量{0,1,2}，以此类推 n 元逻辑变量为{0,1,2,3,4,···,n-1}，其中 n 为有限值。用0-1布尔代数法进行逻辑表达式的运算及简化时一般需要掌握布尔代数的基本定律、结合律、交换律、分配律、互补律、0-1律、吸收律、还原律、狄摩根定理、分解定理等；以及一些规则，如代入规则、反演规则、对偶规则及一些常用的恒等式等[2]。布尔代数基本逻辑关系有，与逻辑：F=A·B；或逻辑：F=A+B；非逻辑：F=A¯。在多元逻辑代数中与逻辑：F=A·B和或逻辑：F=A+B成立但是其中的A和B必须为同维度变量，即A和B的逻辑变量数必须相同。在0-1逻辑代数基础上研究3元及3元以上逻辑代数，即 {0,1,2}，{0,1,2,3}，{0,1,2,3,4,···,n-1}（其中 n 为有限值），的运算性质。

在3元逻辑代数中，即逻辑变量为{0,1,2}，“逻辑与”的计算 0·0=0，0·1=0，0·2=0；1·0=0，1·1=1，1·2=1；2·0=0，2·1=1，2·2=2；“逻辑或”的计算 0+0=0，0+1=1，0+2=2；1+0=1，1+1=1，1+2=2；2+0=2，2+1=2，2+2=2；在4元逻辑代数中，即逻辑变量为{0,1,2,3}，“逻辑与”的计算 0·0=0，0·1=0，0·2=0，0·3=0；1·0=0，1·1=1，1·2=1，1·3=1；2·0=0，2·1=1，2·2=2，2·3=2；3·0=0，3·1=1，3·2=2，3·3=3；“逻辑或”的计算0+0=0，0+1=1，0+2=2，0+3=3；1+0=1，1+1=1，1+2=2，1+3=3；2+0=2，2+1=2，2+2=2，2+3=3；3+0=3，3+1=3，3+2=3，3+3=3；在n元逻辑代数中，即逻辑变量为{0,1,2,3,4,···,n-1}（其中n为有限值）“逻辑与”的计算F=A·B取决于A和B中值小的一个，“逻辑或”的计算F=A+B取决于A和B中值大的一个。

表1 电工考试总成绩真值表

2 多元逻辑代数的基本运算法则和基本定律

2.1 基本运算法则

在 n 逻辑系统中，设 Ln={0,1,2,3,4,···,n-1}，为多元变量的取值集合，且 0＜1＜2＜···＜n-1，那么系统的两种基本运算为

（1）多元“与”运算

n 变量 X1，X2，X3，…，Xm的逻辑“与”，其积 F 为m变量中的最小值，可表示为

式中Xi∈Ln。多元“与”运算也称为最小运算。

（2） 多元“或”运算

n 变量 X1，X2，X3，…，Xm的逻辑“或”，其和 F 为m变量中的最大值，可表示为

式中Xi∈Ln。多元“或”运算也称为最大运算。

（3）多元“与”和多元“或”基本运算法则

0·A=0，n·A=A（A 值≤n），n·A=n（A 值≥n)，A·A=A；

0+A=A，n+A=n（A 值≤n），n+A=A（A 值≥n），A+A=A；

2.2 基本定律

交换律：A·B=B·A，A+B=B+A

结合律：ABC=（AB）C=A（BC），A+B+C=（A+B）+C=A+（B+C）

分配率：A（B+C）=AB+AC，（A+B）（A+C）=A+A（B+C）+BC

其中的A、B和C必须为同维度变量，如同为3值或4值或5值…n值，n为有限项。

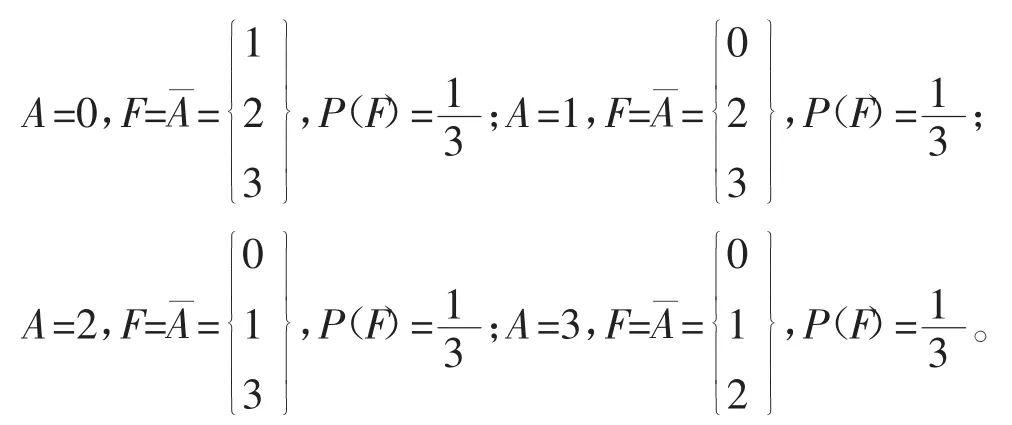
同理n元逻辑代数{0,1,2,3,4,…,n-1}（其中n为有限值）中取值0时F≠0，在n元逻辑空间中除0以外其余值的取值概率为1/n；A取值1时F≠1，在n元逻辑空间中除1以外其余值的取值概率为1/n；A取值n时F≠n，在n元逻辑空间中除n以外其余值的取值概率为1/n。

非逻辑的两个运算性质：在n值逻辑空间{0,1,2,3,4,···,n-1}（其中n为有限值）中有

3 多值逻辑代数的应用初探

3.1 基于多元逻辑代数的小球分拣系统探析

以一个小球分拣系统为例，研究多元逻辑代数在机械系统中的应用。为使研究的问题简化，本文将一些复杂的机械系统简单化、模型化。如图1所示的圆盘小球分拣系统，圆盘以ω的角速度旋转，圆盘有四个不同孔径的孔，分拣四种不同直径的小球（单位：mm），定义有四种孔（单位：mm）：

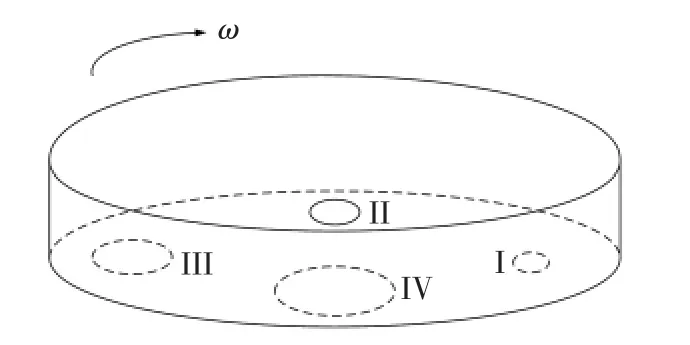
图1 小球分拣系统

定义两个4元逻辑代数变量，孔的逻辑变量定义为A，A的逻辑值为 {0,1,2,3}，ø孔对应的逻辑值取“0”；ø孔对应的逻辑值取“1”；ø孔对应的逻辑值取“2”；ø孔对应的逻辑值取“3”。

小球的逻辑变量定义为B，B的逻辑值为{0,1,2,3}，球对应的逻辑值取“0”；球对应的逻辑值取球对应的逻辑值取球对应的逻辑值取“3”。

I孔逻辑表达式：F1=0·B，即 F1=0，对逻辑表达式的取值进行分析易知I孔仅能分拣的球。II 孔逻辑表达式：F2=1·B，即 F2={0,1}T，对逻辑表达式的取值进行分析可知II孔可以分拣和的球。III孔逻辑表达式：F3=2·B，即F3={0,1,2}T，对逻辑表达式的取值进行分析可知III孔可以分拣的球。IV孔逻辑表达式：F4=3·B，即 F2={0,1,2,3}T，对逻辑表达式的取值进行分析可知IV孔的四种直径的球均能分拣。

对逻辑表达式F的取值进行分析可以得出不同孔的分拣情况，此例虽然较为简单却可以清晰地反映出多元逻辑代数中“逻辑与”在机械系统中的应用和分析方法。

3.2 基于多元逻辑代数的零件配合精度探析

以两个机械零件的配合精度为研究对象，研究多元逻辑代数在机械工程中的另一应用。为使研究的问题更加清晰，现将复杂的机械零件配合精度问题简单化处理。有1号零件的A轴和2号零件的B孔配合，不考虑其他因素的前提下，设定A轴和B孔的配合精度由A轴和B孔的加工精度决定。

规定A轴和B孔有五种加工精度，对应的为IT5、IT6、IT7、IT8、IT9 级。定义两个五维逻辑变量 A和 B，A的逻辑值为 {0,1,2,3,4}，B的逻辑值为{0,1,2,3,4}，A轴、B孔精度与逻辑值的对应关系如表2所列，则1号零件和2号零件配合精度F的表达式为：F=A+B。

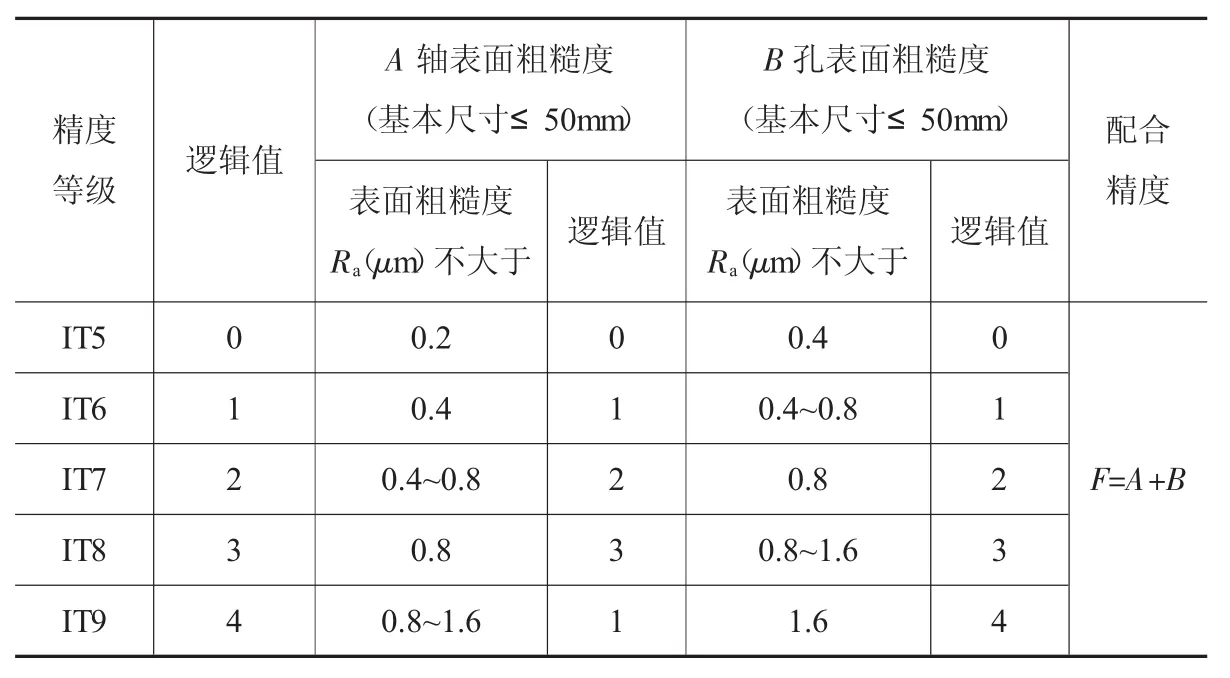
表2 A轴、B孔精度与逻辑值的对应关系[3]

表3 1号零件和2号零件配合精度真值表

由逻辑表达式可得出1号零件和2号零件的配合精度真值表，如表3所示。

对逻辑表达式F的取值进行分析可得出A轴和B孔的配合精度等级。此例是多元逻辑代数在机械工程公差配合部分的典型应用，可清晰反映出多元逻辑代数中“逻辑或”在机械工程中的应用和分析方法。

4 结束语

本文在经典的0-1逻辑代数的基础上引入了多元逻辑代数问题，研究了多元逻辑代数“逻辑与”和“逻辑或”的运算方法。研究了多元逻辑代数的基本运算法则和基本定律，研究了交换律、结合律、分配率、逻辑非的运算性质。多元逻辑代数可以应用到生产生活及机械工程的多个方面，本文以一个小球分拣系统为例研究了多元逻辑代数“逻辑与”的应用，以两个机械零件轴孔配合精度为例研究了多元逻辑代数“逻辑或”的应用。随着现代科学技术的不断发展，大型复杂系统的研制日益增多，对其可靠性、维修性及有效性的分析与评定已成为系统研制过程中不可缺少的重要组成部分[4]。相信随着多元逻辑代数这一全新概念的引入，与其相关的一些理论和规律将会进一步发展和完善，多元逻辑代数在机械可靠性、有效性及故障分析等方面必将有其独到建树。