巧借空间向量，妙解平行问题

☉江苏省华罗庚中学 席国金

我们知道，空间向量可以用来处理空间中有关线、面平行的关系（包括线线平行，线面平行，面面平行），其实质就是把空间中的点、线、面、角等问题利用空间坐标的代数形式表示出来，然后利用空间向量的线性关系或空间向量的数量积，通过代数运算来解决对应的平行问题.

一、线线平行问题

利用空间向量解决线线平行问题的常见方法：证明两直线的方向向量共线.

例1 如图1，ABEDFC为空间多面体，平面ABED与平面ACFD垂直，点O在线段AD上，OA=1，OD=2，△OAB，△OAC，△ODE，△ODF都是正三角形.证明直线BC∥EF.

分析：通过建立相应的空间直角坐标系，找出相应点的坐标及对应的空间向量的坐标，利用两空间向量平行的特点来证明相应的线线平行关系.

图1

图2

证明：过点F作FQ⊥AD，交AD于点Q，连QE，由平面ABED⊥平面ADFC，知FQ⊥平面ABED，以Q为坐标原点，Q—→E为x轴正向，Q—→D为y轴正向，Q—→F为z轴正向，建立如图2所示空间直角坐标系Q—xyz，

点评：判定空间线线的平行问题，利用空间向量的代数运算形式，通过计算两直线所在的方向向量互为共线的关系，确定两对应的方向向量互相平行，进而判定线线的平行问题.这样处理往往可以省去几何证明中的严格的叙述，以代数运算的形式通过计算来达到证明的目的，这样可以省去不必要的逻辑推理与分析，更为简单.

二、线面平行问题

利用空间向量来解决线面的平行问题的常见方法：①证明该直线的方向向量与对应平面的某一法向量垂直；②证明直线的方向向量与对应平面内的某直线的方向向量平行.

例2 如图3所示，在四棱锥P—ABCD中，PC⊥平面ABCD，PC=2，在四边形ABCD中，∠CBA=∠BCD=90°，AB=4，CD=1，点M在PB上，PB=4PM，PB与平面ABCD成30°的角.求证：CM∥平面PAD.

分析：先根据题目条件，以C为坐标原点建立相应的空间直角坐标系，结合线面角的定义确定对应的边长问题，进而确定对应顶点的坐标，通过平面PAD的一个法向量n的求解，结合n·C—→M=0的确定来判断n⊥C—→M，进而结合线面平行的判定定理加以证明.

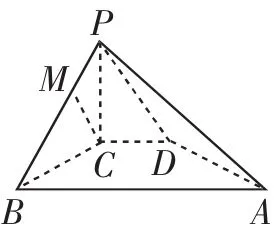
图3

图4

解析：以C为坐标原点，CB为x轴，CD为y轴，CP为z轴建立如图4所示的空间直角坐标系C—xyz.

因为PC⊥平面ABCD，所以∠PBC为PB与平面ABCD所成的角，所以∠PBC=30°.

设n=（x，y，z）为平面PAD的法向量，

又CM⊄平面PAD，所以CM∥平面PAD.

点评：判定空间线面的平行问题，往往直接利用直线的方向向量与对应平面的法向量的数量积为0，通过空间向量的代数形式的运算，及两空间向量的垂直关系的转化，解决有关线面平行的问题.

三、面面平行问题

利用空间向量解决面面平行问题的常见方法：①证明两平面对应的法向量为共线向量；②转化为线面平行、线线平行的问题来处理.

例3 已知平面α内的三点A（2，0，0），B（0，0，2），C（0，2，2），平面β的一个法向量为n=（2，0，2），则不重合的两个平面α和β的位置关系是______.

分析：根据平面α内的三点的坐标来确定相应的向量坐标，进而求解平面α的一个法向量，结合平面β的一个法向量得到对应的共线关系，进而得以判定面面平行.

设m=（x，y，z）为平面α的法向量，

不妨设z=1，可得m=（1，0，1）.

又平面β的一个法向量为n=（2，0，2），

可得n=2m，即m∥n，故α∥β.则填答案：平行.

点评：判定空间面面的平行问题，如果利用两平面的法向量的平行来证明，直接利用空间向量的代数形式的运算即可；而如果利用线线平行、面面平行的判定定理及空间向量来表示与转化，还要说明相应判定定理的条件，千万不能遗漏.

四、平行的探索问题

通过利用空间向量来探究与平行有关的存在性等问题，将几何证明转化为空间向量的计算问题，大大降低了对空间想象能力的要求.对于这类存在性问题，一般是先假设其存在，然后利用空间向量的运算，依据题中的条件求解、检验、判断.

例4 （2016·北京理·17（3））如图5，在四棱锥P—ABCD中，平面PAD⊥平面ABCD，PA⊥PD，PA=PD，AB⊥AD，AB=1，AD=2，AC=CD=.在棱PA上是否存在点M，使得BM∥平面PCD？若存在，求的值；若不存在，说明理由.

分析：取AD的中点O，证明PO，OC，AD两两互相垂直，进而建立对应的空间直角坐标系，利用空间向量的表示，先求解平面PCD的法向量，再假设点M在棱PA上，设出A—→M=λA—→P，根据参数的取值的存在性来分析与判断对应点的存在性问题.

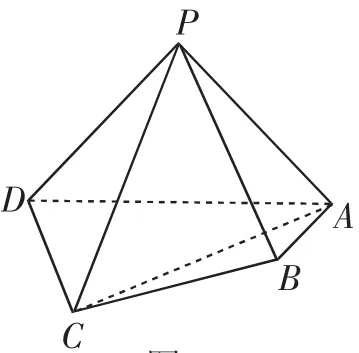
图5

图6

解析：如图6，取AD的中点O，连接PO，CO.

因为PA=PD，所以PO⊥AD，

又因为PO⊂平面PAD，平面PAD⊥平面ABCD，所以PO⊥平面ABCD，

因为CO⊂平面ABCD，所以PO⊥CO，因为AC=CD，所以CO⊥AD，

如图6建立空间直角坐标系O—xyz，

由题意得，A（0，1，0），B（1，1，0），C（2，0，0），D（0，-1，0），P（0，0，1），

点评：解决立体几何中的此类问题时，通常利用空间向量的运算来逆推，目标明确，要注意推理过程是否可逆，不要把必要条件当作充分条件来处理.通常假设题中的数学对象存在（或结论成立），然后在这个前提下进行对应的逻辑推理，若能推导出与条件吻合的数据或事实，则说明假设成立，即存在，并可进一步证明与求解；若推导出与条件或实际情况相矛盾的结论，则说明对应的假设不成立，即不存在.

其实，利用空间向量解决立体几何中的平行关系时，可以通过建立空间直角坐标系，利用空间向量的坐标运算或数量积得出平行关系.当遇到不适合建立空间直角坐标系的问题时，也可以根据题意在立体几何图形中选取一个基底，然后将所需的空间向量用此基底表示出来，再利用向量的运算或数量积进行求解或证明即可.J