构造法在高中数学解题中的应用

☉江苏省新沂市第一中学 徐 剑

数学思想方法结合构造技巧，能使我们领悟数学的价值，形成一整套行之有效的数学学习方法与思想，从不同的角度、不同的知识层面来看待高中各种各样的复杂数学应用题型，紧跟教师课堂的教学步骤，从单一的思维模式中解放出来，探寻一种高效率、高质量、高保证的数学学习模式.

一、注重构造法的理念，训练和解决数学问题

我们在利用“构造法”进行解答数学例题之前，要先了解构造法的概念.首先，“构造”就是为达到某一目的，要采取一系列的方案和手段，制作出步骤及相应的流程来完成这个目的.我们可以选择某种合理的、能促进自己理解的方式去达到提高解题效率的成果，强有力地锻炼自身的数学思维逻辑，无论遇到多么复杂的数学题目，都能进行化简，从而把它们变成日常练习过的简单例题，有效的解答，全方面地学好数学.方程作为高中数学的重要内容之一，涉及很多难理解的知识层面，它与代数式，各种复杂的函数相连接，还与不等式等章节密切不可分，我们在做特殊方程的例题时，要充分利用构造法，依据方程理论，加深对数学应用题的理解和记忆，循序渐进，反复训练，能使许多的问题得以转化，从而得到解决，经历一个反复思考的数学学习过程，把生活中的各种数学分类迁移到数学中来，挖掘教材提供的机会，并根据数学的特殊性质，对自己负责，逐渐养成学习数学的良好习惯.

数学中的构造法有效而特殊，会让我们有“似曾相识”的感觉，它是为了对数学学科的研究和日常的解题方便而采用的一种思想.它能激发我们的学习思维，让我们在头脑中能有一种潜意识，从而进行不断的知识迁移和扩展、数学定理的推移、数学证明的猜测和结合等，通过各种手段，让原来一个复杂的数学过程变得通用化、简单化、快捷化.对于一些复杂的三角函数例题，由于存在特殊的函数角度，不方便直接求解，这时就需要采用构造法.

例1 求sin20°cos70°+sin10°sin50°的值.

解析：不能直接求出来，需要借用“构造法”，引入几个特殊值，所求式子与和差角公式结构一致，达到构造和提高解题效率的目的.我们可以令x=sin20°cos70°+sin10°sin50°，y=cos20°sin70°+cos10°cos50°，构造出两个方程表达式，则x+y=sin20°cos70°+sin10°sin50°+cos20°sin70°+cos10°cos50°=sin90°+cos40°=1+cos40°. 同理，x-即sin20°cos70°+sin10°sin50°的值为，就完成了解答过程.这样一个构造的解题过程，能扭转一些数学解题困局.我们要不断估计和推理，把普遍问题类比为特殊问题等，获取最佳的解答方案.

二、广泛应用构造思想，多角度思考和理解问题

在数学界有许多的数学家都是勤勤恳恳地利用自己的学习经验，借助构造法发现并证明了许多十分有用的数学定理.例如，欧几里得、洛必达研究的洛必达法则；欧拉研究的欧拉不等式；拉格朗日研究的中值定理等，大多都用“构造法”解决了许多的数学难题，为我们开辟了数学道路.我们要向前辈学习，运用一系列的数学定理和数学推理，自行构造和解答，学会从一个数学角度转移到另一个角度或者层面，从一个对象获得另一个对象的性质，养成学习数学的好习惯，逐渐加强构造法的力度，完善有效数学学习方法.构造法是一种重要的数学解题方法，我们在解题过程中要注重构造思想的实际效果，合理应用构造思想，对题目进行整理和分析，学会实质性的训练和不断的探索创新，不断的感知数学公式、概念，遇到复杂的题目时，换一个角度去思考，去理解，去感悟，从而找到一条绕过障碍的新途径.

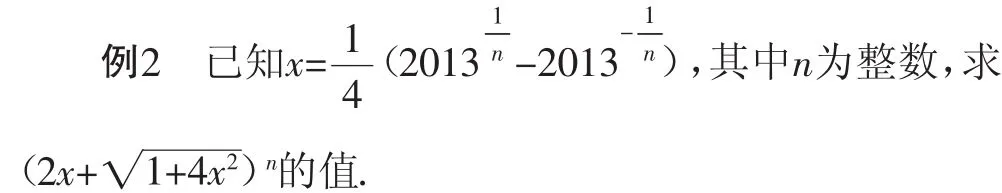
解析：这是一道复杂的代数求解问题，首先得看清已知条件是什么，不能匆忙下手，更不能胡乱拉取数学公式，造成解题思路的混淆，而是要通过已知条件选择更简单的解题方法.通过对题目的详细观察，不难发是倒数关系，这时可以设a和b是方程t2-4xt-1=0的两个实数根，又因为a＞b，所以最终解得（）n的值为2013，这是2013年的高考真题.我们可以到书店购买一些实质性的学习资料和数学真题，时常练习，发现数学例题的解答规律，形成常规题型的解题思路和模式，正视自己的数学学习基础，并结合各类数学概念和公式，做好必要的笔记，及时复习和巩固.

三、引入构造法的模式，全面提高解题效率

在对构造法的应用过程中，我们要不断地引入构造法的模式，全面提高数学解题效率，可以借鉴课内外的书籍，加强自身的数学素质培养.国内外就有许多的研究成果，如西方的《几何原本》和中国的《九章算术》等都详细地记载了数学学习的方法，对我们的学习效率和技巧很有帮助.我国的构造法主要是针对当前数学学科的特殊性，注重问题的能行性，引出一系列的方法和模式，许多古典的书籍和书籍中的数学例题对推动中国数学的发展起到了深远的影响，我们一定要合理地运用和练习，从各个角度寻求数学例题的解题思路，遇到不懂的问题多思考、多求解、多询问，循序渐进地提高自己的数学能力.构造法是一种极其富有技巧性和思维创造性的常用解题方法，需要我们了解自己所需要的数学模型和接受知识的能力和基础，并根据数学的特殊性质，全面地进行归纳和理解，和同学老师做好沟通交流，取长补短地提高自己的实际能力，构造出一种新的问题形式，丰富自身内涵，从数学例题中领悟数学的学习技巧，构造出具体的结果，从而绕过解题障碍，明确构造的目的和做题时的最终结果，全方面地通过用心观察、仔细联想，采用新的学习方法，把数学题目中的已知的关系式为“支架”，真正体验一种创造性思维的构思过程，在把握渗透契机的同时，往往能使许多复杂的数学问题在新的关系下得以转化，许多不懂的问题也可以很快解决.

另一方面，当今的计算机科学和各类的财经类专业，都离不开数学这一门学问，在很大程度上是靠数学来发展的，无论我们今后从事什么职业，都要运用数学的知识来解答一些实质性的问题.因此，我们高中生必须从现在做起，吸取生活中各种各样有价值的数学学习元素，打好数学基础，凭借结构上的数学相似性，找到数学例题的解题突破口，把定理和公式合理结合在一起，才能极大降低数学例题的难度，通过适当的调节和代换，以及相应的变形，适当的时候结合图像进行分析和揣摩，抓住解题的关键点，分析、发现数学问题的各个环节，以及它们之间的联系，从而达到事半功倍之效.

例3 已知x+y+z=0，xyz=8，求z的取值范围.

解析：构造一个以x，y为根的一元二次方程t2+bt+c=得z<0或z>.构造法在解题时的便捷性由此可见.

数学学习是循序渐进的学习，不断积累学习经验的一门学科，我们一定要学会把“构造法”加入到各种复杂的数学例题解答过程中，充分转化和化简，并通过自己的学习经验发现数学的真谛.在解答各类题型时，一定要注重构造法的理念，训练日常数学课堂例题，经历一个认真总结、积累经验的数学探索和学习过程，才能逐渐地加强构造法的力度，完善有效数学学习方法，最终引入构造法的模式，全面提高数学解题效率.J