培养解题能力的“四化”策略——从向量加法的“平行四边形法则”说起

☉江苏省海安曲塘中学 狄玉兰

在高三数学复习中，采用何种方式，才能既巩固基础，又能促进学生解题能力的提升？这是困扰广大一线教师的一个难题.如果只是将知识点简单、机械地重复一遍，并不能达到上述目的.笔者教学中发现，从一个最基本问题出发，通过将问题变化、拓展，建立其与其他知识之间的关联，对于构建知识网络、提高解题能力，可收到事半功倍之效.本文以苏教版必修4中向量求和的平行四边形法为例说明.

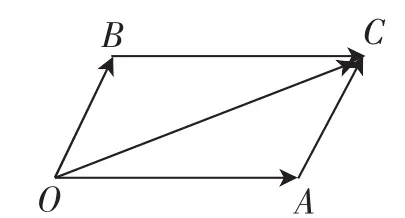
图1

两向量求和的平行四边形法则：如图1所示，以同一点O为起点的两个向量O—→A，O—→B为邻边作平行四边形OACB，则以O为起点的对角线O—→C就是O—→A+O—→B.

一、将问题“变化”，巩固“四基”

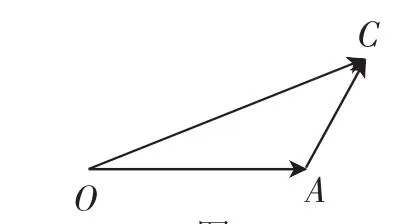
图2

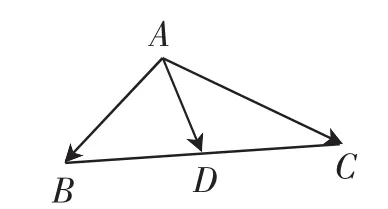
图3

通过上述几种变化将向量加法的平行四边形法则，三角形法则，减法的三角形法则以及中线向量公式连成一线，实现了基础知识的巩固.

二、将问题解法“一般化”，培养思维的概括能力

设e1，e2是同一平面内两个不共线的向量，a是这一平面上的任意一个向量，根据向量的定义，将它们置于同一起点，设=a（如图4所示），过点C作OB的平行线，交OA或其延长线于点M，过点C作OM的平行线，交OB或其延长线于点N.则存在实数

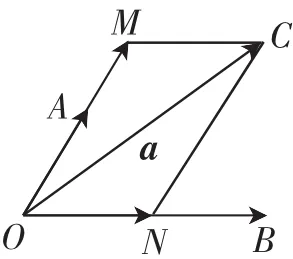
图4

进而得到了平面向量的基本定理：

变化5：如果e1，e2是同一平面内两个不共线的向量，那么对于这一平面内的任意一个向量a，有且只有一对实数λ1，λ2，使得a=λ1e1+λ2e2.其中这组不共线的向量e1，e2叫做表示这一平面内所有向量的一组基底.

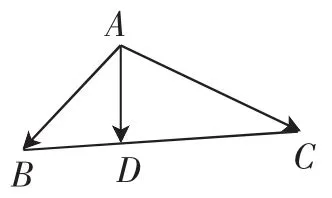
图5

变化7：A、B、C为平面内不共线的三点，D为平面ABC上一点，且，则B、C、D三点共线.

三、将例问题“深化”，培养思维的广阔性和深刻性

例1（2016年江苏卷）如图6所示，在△ABC中，D是BC的中点，E，F是AD上的两个三等分点的值是______.

图6

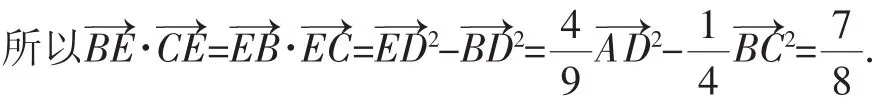
将问题深入探究形成结论，为我们解题提供了便利.

四、将问题“类化”，展现通性通法

例2 已知e1、e2为平面上的单位向量，e1与e2的起点均为坐标原点O，e与e的夹角为.平面区域D由所有满足的点P组成，其中λ+μ≤1，λ、μ≥0，那么平面区域D的面积为（ ）.

解析：由题目条件及变化9易知平面区域D为边长为1的等边三角形，其面积为

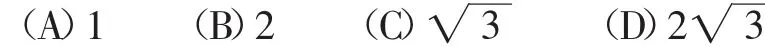
解析：由题目条件及变化10易知平面区域内所有点P构成的图形为三角形，其底为，高为2，故面积为.故选C.

将形异质同的问题类化后，找到统一的解答思路，形成了通法，落实了能力.

综上，本文从一个教材结论出发，站在整体高度上，从不同角度进行变化、拓展，将所涉及的知识由点及线、由线及面，构建知识网络，既落实了知识的系统学习，又促进了学生解题能力提升.J