基于特征值的单机无穷大电力系统随机稳定性分析

张 振， 刘艳红(郑州大学 电气工程学院，河南 郑州 450001)

0 引言

电力系统的短路故障和控制等是研究人员长期关注的研究课题[1-2]. 电力系统在运行过程中不可避免地受到负荷波动、控制回路噪声、电网谐波、随机故障等随机扰动的影响.随着现代电力网络规模不断扩大，新能源发电与并网以及电动汽车的使用，使得电力系统受到的不确定随机扰动进一步增加，对系统稳定性和电能质量造成的影响不容忽视[3-5].

电力系统中的随机因素可概括为3类：①外部随机扰动；②系统初值的随机性；③系统参数的随机性. 文献[6-7]考虑外部随机扰动下系统建模与稳定分析，针对随机扰动下的电力系统的稳定性分析问题，建立了系统的随机动态模型，结合随机系统p阶矩稳定性理论，通过求解显示解分析了系统的均值稳定、均方稳定性. 多机电力系统的随机小扰动稳定性问题与单机系统类似，但要考虑系统之间的相互影响[8-9]. 基于电力系统动态模型对电力系统小扰动概率稳定性分析，可以得到随机扰动下系统关键特征根位于左半平面的概率[10-11]. 但上述研究结果均未给出随机扰动与无扰动系统稳定性之间的定量关系，无法准确估计在给定随机扰动强度条件下系统响应的均值均方差的界，也没有讨论扰动强度和系统参数对均值均方差界的影响.

笔者研究了随机扰动下单机无穷大电力系统的随机稳定性.首先建立了单机无穷大系统的随机动态模型，采用随机微分理论[12]和矩阵论[13]相关知识给出了系统均值均方稳定的条件，分析了系统均值均方差的界与随机扰动强度之间的关系，并讨论了系统矩阵特征值和系统参数对系统均值和均方差的界的影响， 最后，通过对随机扰动下的电力系统进行仿真分析，验证了所得结论的正确性.

1 电力系统随机动态模型

图1所示为单机无穷大系统.

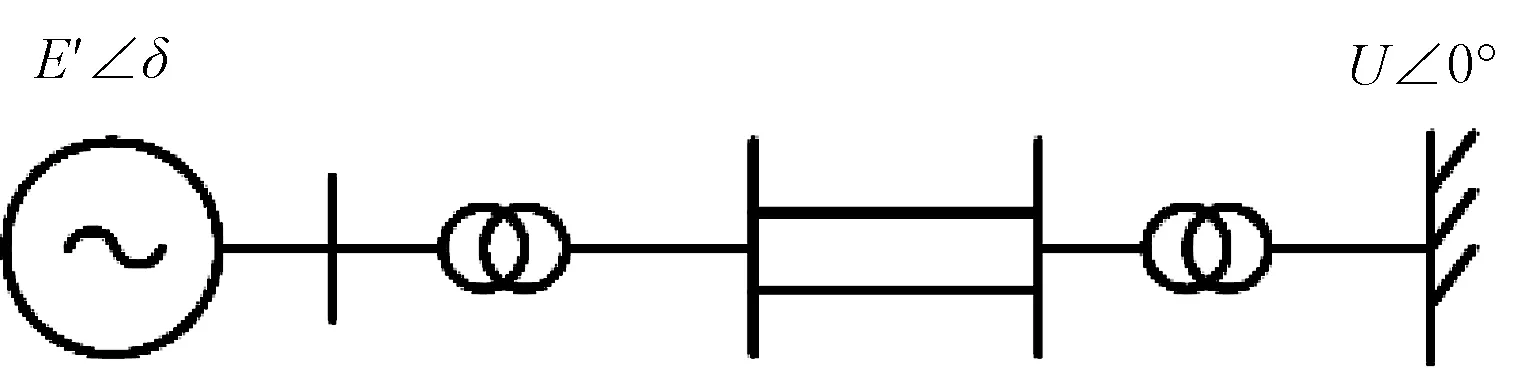
图1 单机无穷大系统Fig.1 Single machine infinite bus system

无随机扰动下系统的动态模型表示为[14]：

(1)

式中：D为阻尼系数；M为惯性时间常数；δ为发电机功角；ω为转子角速度；ω0为同步角速度；Pm为发电机输入机械功率；Pe为发电机输出的电磁功率，且

(2)

(3)

式中：E′为发电机内电势;U为无穷大母线电压；XΣ表示总电抗,δ0为系统平衡状态对应的功角.

考虑新能源发电、电动汽车等对电力系统所产生的随机扰动，并将其近似看作高斯过程[7]，电力系统的随机动态模型表示为：

(4)

式中：W(t)为高斯过程；σ为随机扰动强度.

将系统在平衡点处线性化，并注意到：

(5)

电力系统动态模型可表示为下面标准随机系统：

dx(t)=Ax(t)dt+A′dB(t),

(6)

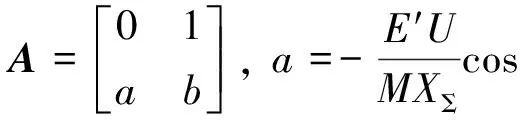
2 随机电力系统均值均方稳定性

本节讨论电力系统的均值和均方稳定性，并建立系统均值和均方差的界与随机扰动强度及系统参数之间的关系.

定义1：对于系统(6)，若其解过程x(t)满足：

(7)

式中：ε是正常数，则系统是p阶矩稳定；特殊的，p等于1、2时，称系统是均值、均方稳定；当ε→0时，称系统是p阶矩渐近稳定.

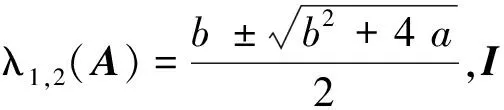
定理1：若矩阵A的特征方程的根为重根，则

(8)

若矩阵A的特征方程无重根且为实数，则

(9)

若矩阵A的特征方程无重根且为复数，则

(10)

式中：γ1、γ2、γ3是关于a、b的量.

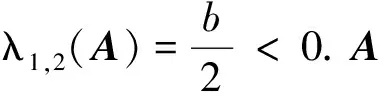
由函数f(x)在λi处可展开表示为:

(11)

式中：i=1,2. 将R代入上式得:

(12)

令f(x)=ex，有

(13)

(2) 若矩阵A的特征方程无重根且为实数，有

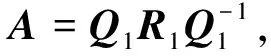
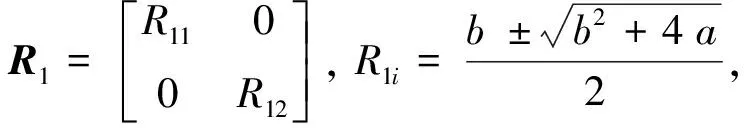
将R1i带入f(x)，令f(x)=ex，整理得：

eR1i=eλi(A).

(14)

(3) 若矩阵A的特征方程无重根且为复数，即：

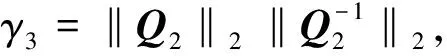
定理2：对随机电力系统(6)，若Re{λ1,2(A)}<0，那么系统是均值稳定的，且满足：

(i) 矩阵A的特征方程有重根,有

(15)

(ii) 矩阵A的特征方程无重根且为实数，有

(16)

(iii)矩阵A的特征方程无重根且为负数，有

(17)

证明：对于系统(6)的解的显式表达式为：

(18)

有

E[xT(t)x(t)]=E[(eAtx0)TeAtx0]+

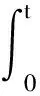
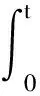
(19)

非随机变量的期望等于本身，有

(20)

根据维纳性质，有

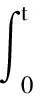
(21)

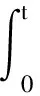
(22)

对式(19)等号右边第四项根据维纳过程的随机积分性质，有

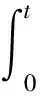
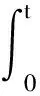
(23)

把式(20)～(23)带入式(19)得

(24)

(i) 若矩阵A的特征方程有重根，有

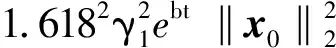
有

故

(25)

根据Couchy-Schwarz不等式

则

(26)

(ii) 矩阵A的特征方程无重根且为实数，同理可得:

(27)

(iii) 矩阵A的特征方程无重根且为实数，有

(28)

综上，存在

满足：

(29)

则系统(6)是均值稳定的.

定理3：对随机电力系统(6)，若Re{λ1,2(A)}<0，那么系统是均方稳定的，且满足：

(i) 矩阵A的特征方程有重根，有

(30)

(ii) 矩阵A的特征方程无重根且为实数，有

(31)

(iii)矩阵A的特征方程无重根且为负数,有

(32)

证明：由定理1知

(i) 矩阵A的特征方程有重根，有

(ii) 矩阵A的特征方程无重根且为实数，有

(iii)矩阵A的特征方程无重根且为负数，有

(33)

则系统(6)是均方稳定的.

注1：定理2所得结果可推广到n维随机电力系统. 具体地，将n维随机电力系统化为方程(6)所示标准随机动态系统形式，由定理2的证明过程知方程(24)仍成立. 进一步，根据矩阵特征值分析方法得到‖eA‖2以及‖A′‖2的表达式，并根据矩阵A特征值的不同取值情况得到方程(24)的不同表达式，与定理2类似可判断系统的均值均方稳定性.

3 仿真算例

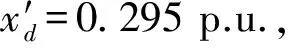
系统的系数矩阵为：

λ1，2(A)=-0.000 4±0.023 8j;

R2=

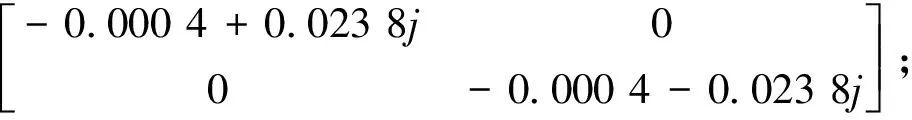
Q2=

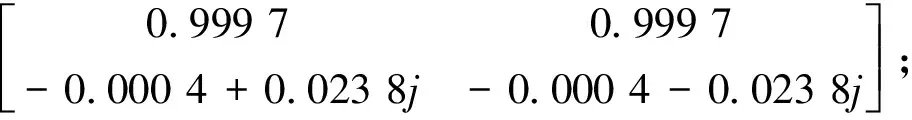
综上知Re{λ1,2(A)}<0，则系统(6)在无扰动下是局部渐近稳定，在随机小扰动下是均值、均方稳定.

下面对不同随机扰动强度作用下系统的稳定性进行仿真. 系统状态均值和均方差的界如表1所示，显然随着σ的增加，系统均值和均方差的上界也增加.不同扰动强度下的仿真结果如图2～7所示.

表1 均值均方差的界Tab.1 The bounds of mean and mean square error

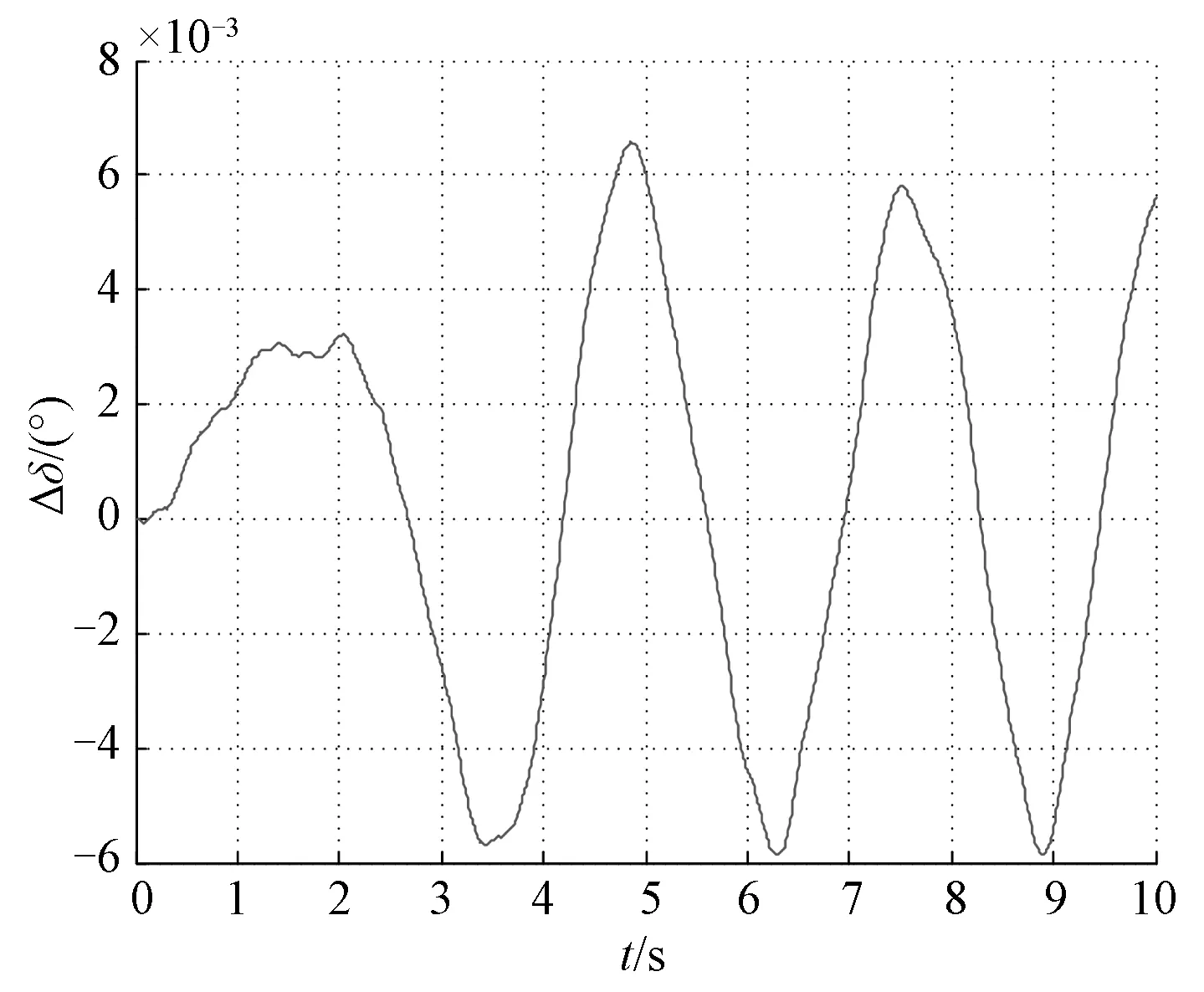
图2 σ=0.02时的Δδ响应曲线Fig.2 Response of Δδ with σ=0.02

图3 σ=0.02时的Δω响应曲线Fig.3 Response of Δω with σ=0.02

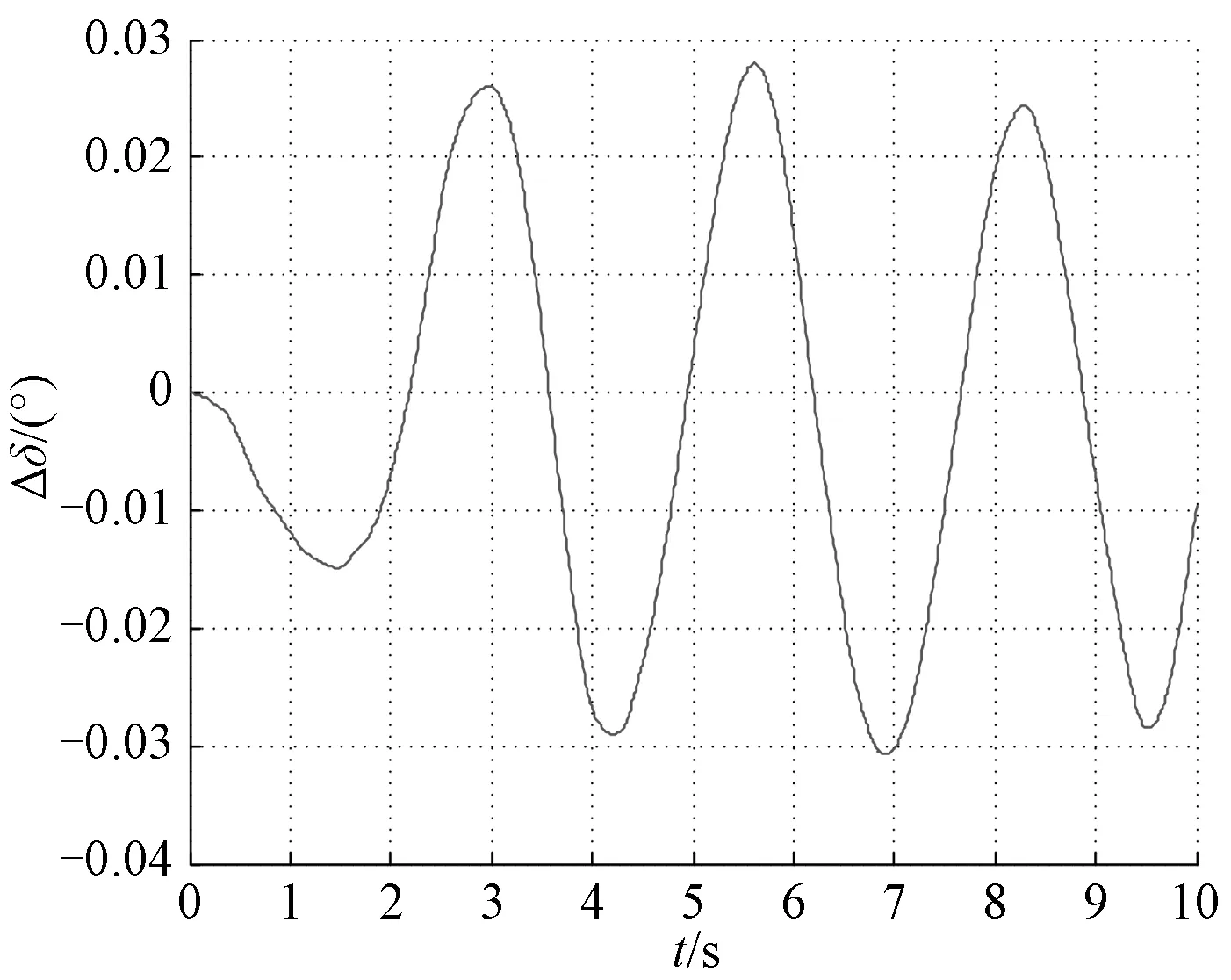
图4 σ=0.04时的Δδ响应曲线Fig.4 Response of Δδ with σ=0.04

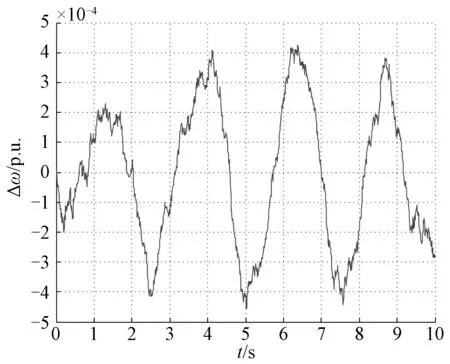
图5 σ=0.04时的Δω响应曲线Fig.5 Response of Δω with σ=0.04

图6 σ=1.50时的Δδ响应曲线Fig.6 Response of Δδ with σ=1.50

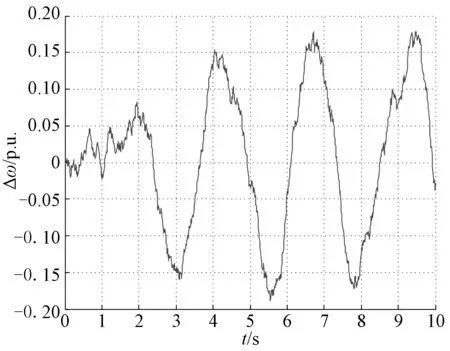
图7 σ=1.50时的Δω响应曲线Fig.7 Response of Δω with σ=1.50

从图2～5可以看出，当取σ=0.02,σ=0.04，即系统在较小随机扰动作用下，功角及角速度变化量很小，能够稳定运行在扰动前的平衡状态，但图4中系统功角的变化峰值较图2有比较明显的增大，图5所示角速度变化量较图3也有明显的增大，表明随着随机扰动强度的增大，系统状态的波动增加. 由仿真结果图6和图7可知，当σ=1.50，即在较大随机扰动作用下，系统功角、角速度的波动明显增大，扰动后系统运行点无法稳定在扰动前的平衡状态，系统失稳.

4 结论

笔者对高斯随机小扰动下电力系统的稳定性进行分析. 建立了系统的高斯随机小扰动随机动态模型，研究了电力系统随机小扰动稳定性，给出了系统的均值均方稳定性的条件，通过对系统矩阵特征值的3种不同情况进行分析，给出了系统均值均方差的界与随机扰动强度以及系统参数之间的关系，并在不同随机扰动强度下对系统进行仿真分析. 研究结果表明：随机小扰动不会影响系统的稳定性，但会影响系统均值均方差的界；大扰动不仅会影响系统均值均方差的界，而且会造成系统不稳定. 笔者所提出的分析方法同样适应于高阶随机电力系统的小扰动稳定性分析，且能够准确估计随机扰动和系统参数对系统状态稳定性的影响.