双驱动轴承试验机的负载特性研究
韩红彪,潘荣铭仁
(河南科技大学 机电工程学院,河南 洛阳 471003)
轴承试验机用于测试轴承的各项性能,验证其是否符合设计标准,针对试验中出现的问题改进轴承设计,同时在轴承设计定型后对轴承的质量进行检测。因此,研制相应的轴承试验机对轴承设计和制造至关重要[1-4]。对于某型航空轴承,根据其特殊的实际工况需求,需设计专用的双驱动轴承试验机,为确保试验机正常运行,达到设计条件,需要研究双驱动轴承试验机在不同工作条件下的负载特性,便于正确设计驱动系统和选择电动机。
1 试验机机械结构和受力分析
根据轴承试验要求设计的双驱动轴承试验机的机械原理如图1所示。试验机采用卧式设计,其驱动轴系分为左、右2个部分,每个轴系都由电动机、联轴器、增速箱、主轴和2套支承轴承组成。左、右侧轴系分别驱动轴承内、外圈旋转。通过固定在试验机中部的径向加载液压缸向试验轴承外圈施加径向载荷Fr(不大于18 kN);通过固定在外圈轴系支承轴承4轴肩处的加载液压缸,经支承轴承4的外圈向试验轴承施加轴向载荷Fa(不大于40 kN)。
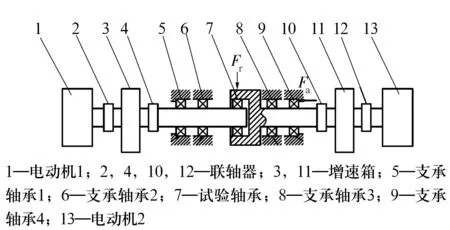
图1 双驱动轴承试验机机械结构简图
根据双驱动轴承试验机的转速控制要求,试验机两侧的电动机需带动试验轴承内、外圈实现同时同向或反向旋转。在试验机进行带载荷试验时,通过增速比为1∶10的增速箱后,试验机主轴转速应达到1 500~10 000 r/min,并可实现在此速度区间内的无级调速。同时,在试验机进行空载极限转速试验时,试验机主轴转速应能达到30 000 r/min。在上述试验过程中,主轴转速误差为±0.5% F.S,主轴的每万转升降速响应时间不超过10 s。
为正确设计驱动系统并选择合适的电动机,就需要分析试验机在不同试验条件下的负载特性。在试验过程中,每个主轴的负载力矩主要是其上各轴承的摩擦力矩和加速/制动力矩,而各轴承的摩擦力矩与其所承受的径向力、轴向力和转速等因素密切相关,需要对每个轴系进行受力分析。右侧轴系的简化受力分析如图2所示(左右两侧轴系的受力对称),图中:0为试验轴承的中心,3和4分别为支承轴承3和支承轴承4的中心,轴承跨距分别为L1和L2。
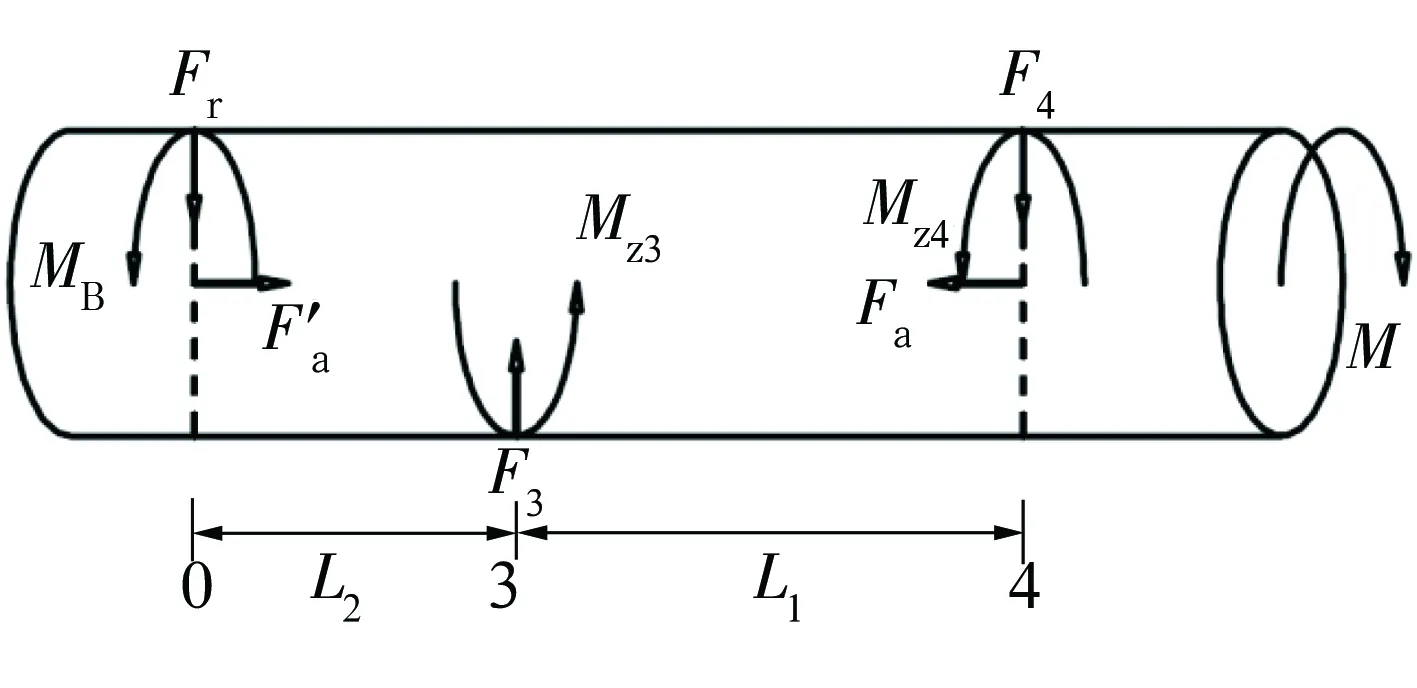
图2 右侧轴系简化受力图
当试验机处于高转速试验阶段时,支承轴承和试验轴承在高速运转的同时受到加载系统所施加的外部载荷的作用,各轴承会产生较大的摩擦力矩,根据力矩平衡公式可得
F3L1=Fr(L1+L2),
(1)
F3=F4+Fr,
(2)
(3)
整理 (1),(2) 式可得
(4)
(5)
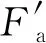
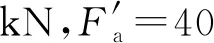
2 负载特性分析
在双驱动轴承试验机轴系中,试验轴承为新型角接触球轴承,单侧轴系采用一对与被测轴承型号相同的角接触球轴承支承。因此,在进行单侧系统中轴承摩擦力矩计算时,需要计算2个支承轴承及试验轴承的摩擦力矩。单侧系统的总扭矩T等于在加速/制动工况下主轴的加速/制动扭矩Ts与各轴承的总摩擦力矩M之和,即
T=Ts+M,
(6)
(7)
则根据对应的工作转速n计算得单侧系统所需的总功率P为
(8)
式中:α为角加速度,r/s2;m为轴系质量,kg;r为轴系平均半径,m;Δω为单位时间转速增量;t为主轴每万转加速时间,s。按照设计要求,α=105 r/s2,r=0.06 m,m=76 kg,t=10 s;将数值代入(6)与(7)式后,计算出主轴的加速/制动扭矩Ts=14.4 N·m。
当进行负载试验时,对于单侧轴系,轴系总摩擦力矩等于各轴承的摩擦力矩之和,即
M=MB+Mz3+Mz4,
(9)
式中:MB为试验轴承的旋转摩擦力矩;Mz3,Mz4分别为支承轴承3、支承轴承4的旋转摩擦力矩。
对于轴承摩擦力矩的计算,经典计算公式在高速运转条件下考虑的变量较少,计算结果并不准确[5]。因此,采用SKF公司提出的计算公式[6],对于试验轴承,其摩擦力矩为
MB=Mrr+Msl+Mseal+Mdrag,
(10)
式中:Mrr为滚动摩擦力矩;Msl为滑动摩擦力矩;Mseal为密封件的摩擦力矩;Mdrag为由于拖曳损失、涡流和飞溅等导致的摩擦力矩。各部分的具体计算可查阅文献[6]。对于轴系中的支承轴承,其摩擦力矩Mz3,Mz4的计算方法与试验轴承的摩擦力矩计算方法相同。
根据上述公式可计算得到不同转速下试验机主轴的负载扭矩和功率。某航空轴承在负载试验(承受最大径向载荷和最大轴向载荷)及空载极限转速试验时驱动系统的负载扭矩/功率随主轴转速的变化如图3所示。
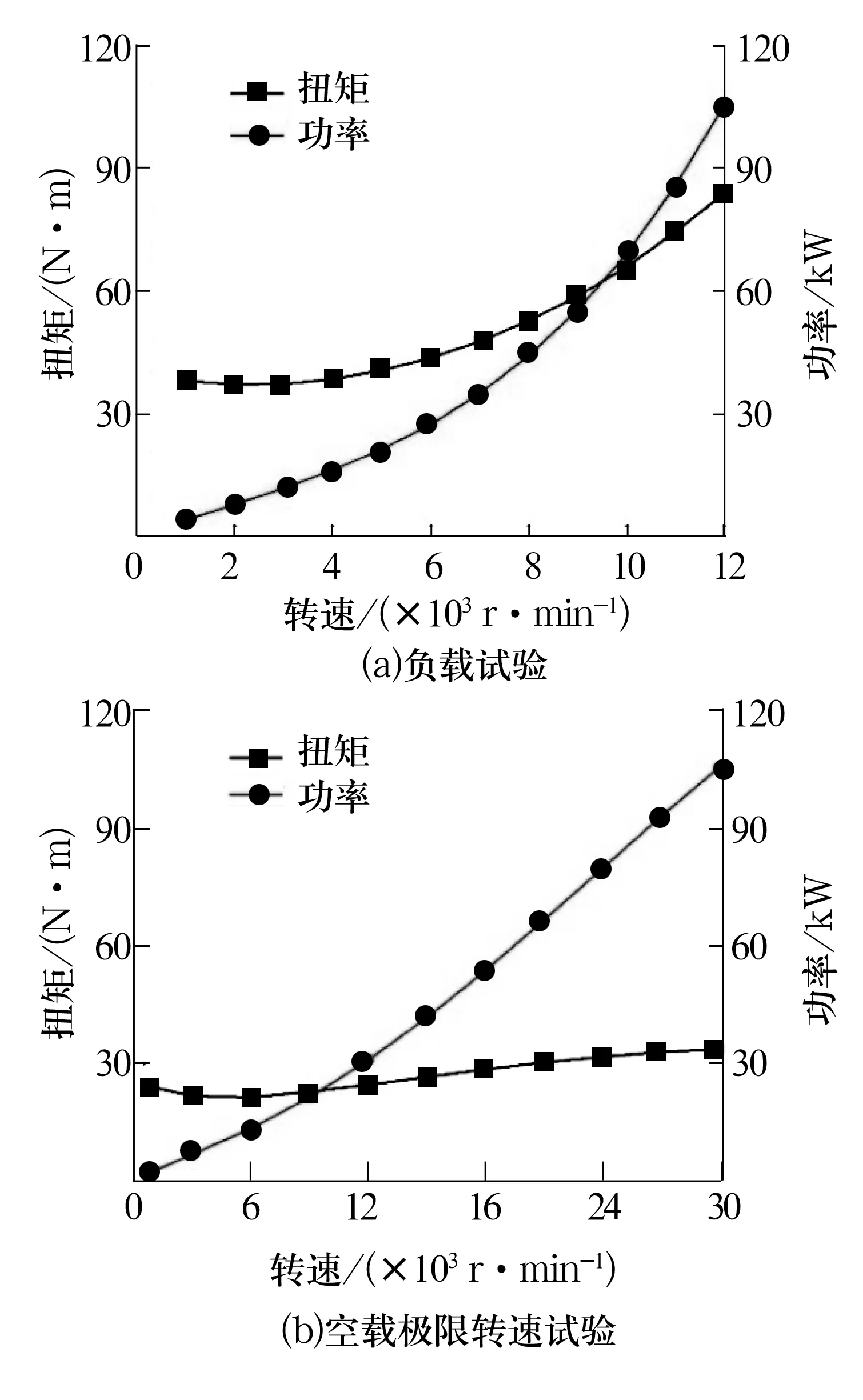
图3 某航空轴承负载扭矩/功率随主轴转速的变化
由上述分析结果可知:负载试验时系统负载扭矩达到最大值,最大扭矩T=83.82 N·m;空载极限转速试验时系统所需功率最大,最大功率P=105.63 kW。
3 电动机和变频器选型
由双驱动轴承试验机的机械结构可知,传动系统中有增速箱、联轴器等环节,增速箱为采用8级精度齿轮的二级增速箱,其传动比为1∶10,每级传动效率η1=0.97;联轴器为梅花接轴联轴器,机械效率η2=0.98。则电动机所需实际扭矩Tc及实际功率Pc分别为
(11)
(12)
计算可得Tc=92.76 N·m;Pc=116.98 kW。由于电动机需要负载启动,并能够在快速加、减速过程中进入瞬时高负载状态;另外,电动机采用恒转矩调速,为与试验机的工况需求相适应,电动机选型时需要足够的功率余量[7]。因此,选择西门子1LE0系列电动机,其主要参数见表1;变频器则选择功率模块为PM240的G120变频器,其额定输出功率为250 kW,额定输出电流为400 A。

表1 电动机主要参数
转速控制系统如图4所示,PLC通过2台变频器分别对两侧轴系电动机进行转速的闭环控制,同时,使用交叉耦合方式对电动机进行同步控制。
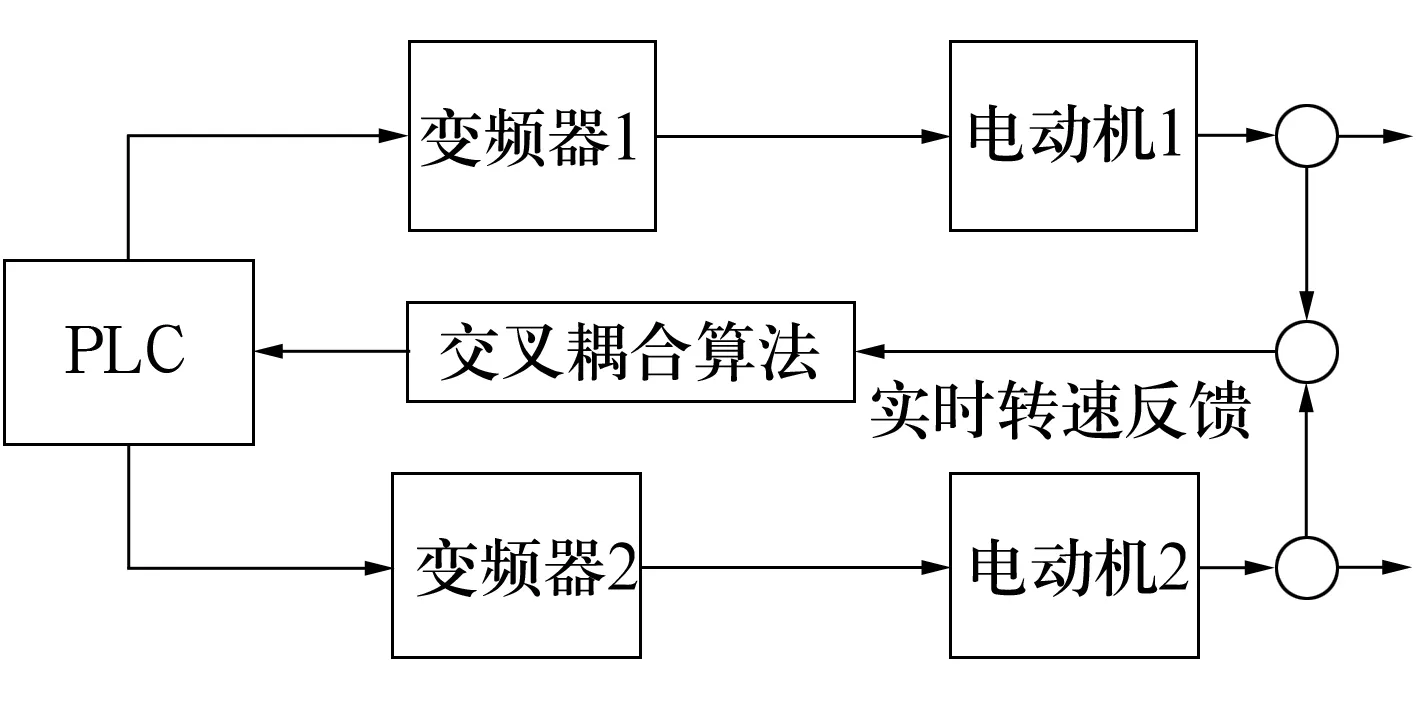
图4 转速控制系统架构图
4 试验验证
根据上述设计选型,将所选用电动机安装在双驱动轴承试验机上进行了试运行,得到了电动机在负载及空转试验时电动机的实际运转数据,结果如图5、图6所示。由于试验机驱动系统的相关采样数据在储存时为断续的值,加之试验时受到扰动,因此实测数据出现离散。
从图5a可以看出:当试验进行至t=7 s时,试验机进行轴向与径向加载,电动机转速出现小幅度的下降,在控制策略的作用下,转速控制系统做出反应并在2 s后继续加速,最终达到并稳定在设定的主轴转速(10 000 r/min),说明电动机满足驱动系统所需的最大扭矩要求。从图6a可以看出:空载极限转速试验共持续45 s,电动机转速在算法控制下呈现相对平稳的上升趋势,在28 s时电动机达到预设转速(30 000 r/min),经过调节后在第31 s时转速达到稳态。试验中电动机最大功率约为120 kW,每万转的加速响应时间均在10 s以内,达到设计中对于电动机每万转升降速响应时间的要求,说明所选电动机满足试验机驱动系统所需的最大功率和加速时间。
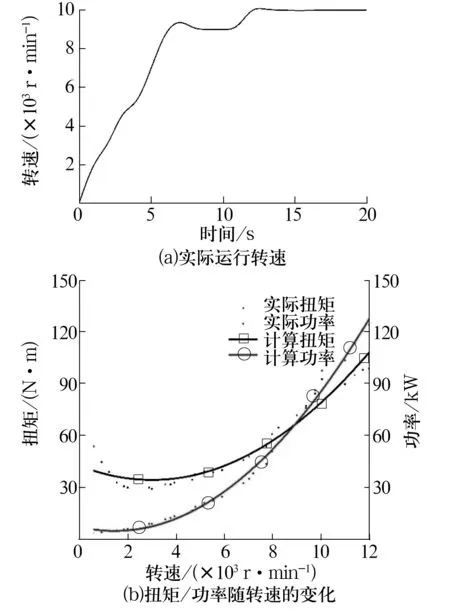
图5 某航空轴承负载试验结果
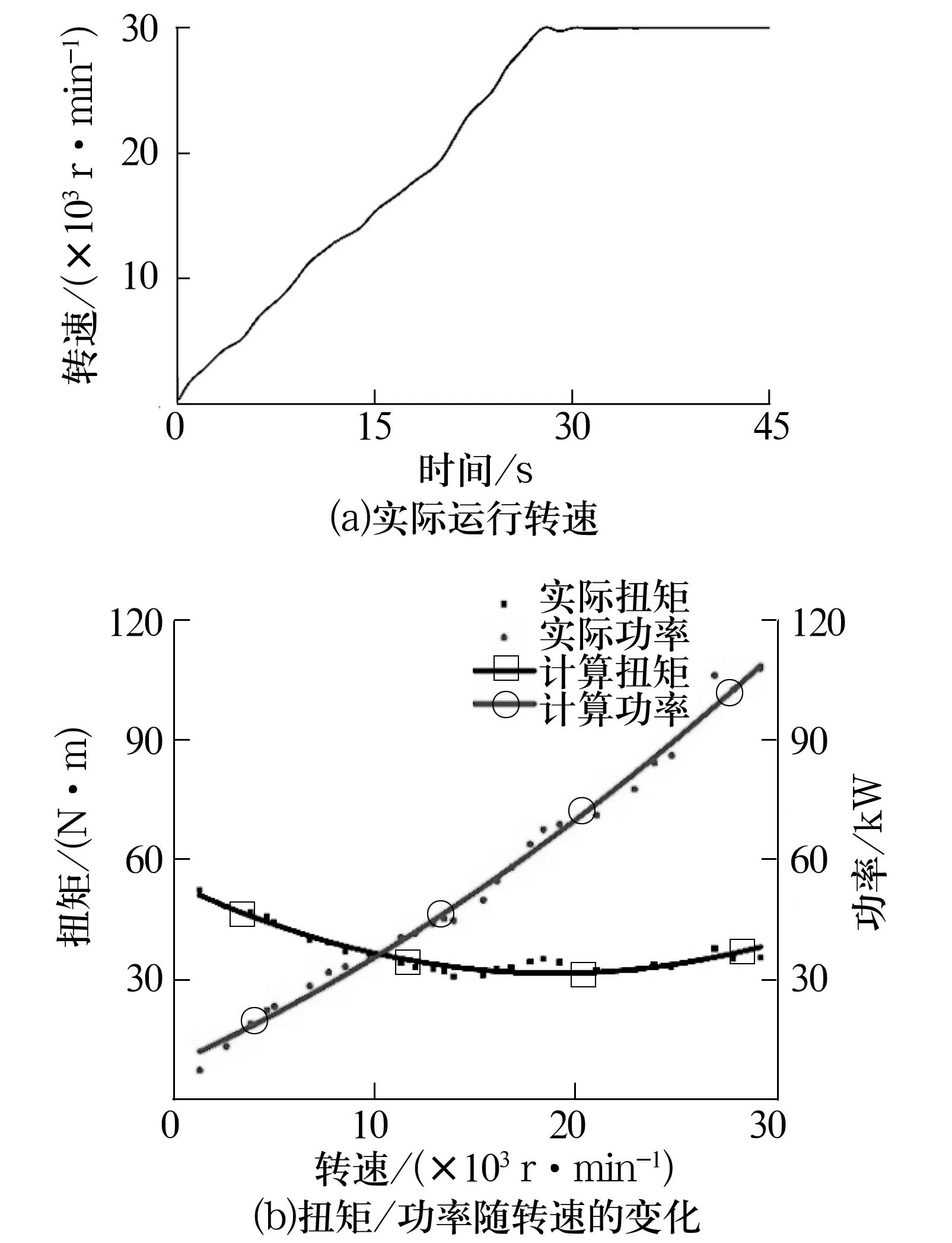
图6 某航空轴承空载试验结果
从图5b可以看出:在低速阶段,由于速度控制策略所设定的加速度较大,导致电动机的实际扭矩相比计算结果较大;随着转速升高,加速度逐渐下降,实际扭矩与计算结果接近;从图6b 看出:电动机的输出功率在低速阶段受速度控制策略影响,与计算结果相比较大;随着转速的升高,加速度逐渐减小并接近计算值;通过多项式拟合法整理试验数据后得到的扭矩/功率曲线的变化趋势逐渐与计算结果相一致,验证了上述计算方法的可靠性。
5 结束语
试验机驱动系统的整体设计满足了某型航空双转子轴承试验所需的高转速、快速响应的要求。通过试验与设计方案相互印证,最终达到新型轴承试验机的设计标准。实际运行中得到的负载特性数据为试验机双驱动系统的转速控制研究奠定了基础,保证了试验机整体的成功研制。该试验机在为我国高转速双转子轴承研制提供了可靠的试验设备的同时,为相关设备的后续研发提供了参考。

