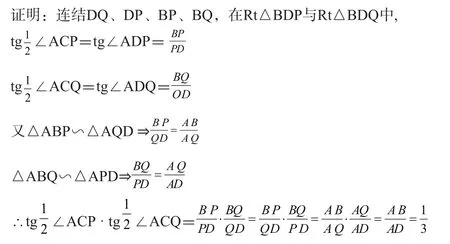例说几何定值的证明方法

（苍溪县龙洞乡中心小学校 四川广元 628442）

几何定值问题，一般觉得束手无策，其原因在于题中没有明确给出这个定值是什么，且此类题目在教材中安排分散，就题论题，没有给出一般的证明策略。

如何发现“定值”是什么，是解决这类问题的关键。寻找定值的方法，一般是把图形中的点或线段运动到特殊的位置进行分析，或将问题转化到特殊的几何图形中，以发现“定值”，然后给出一般的证明。

一、从动点的临界位置发现定值。

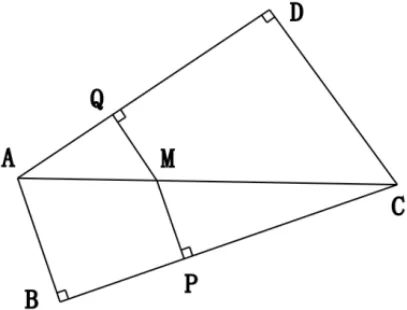
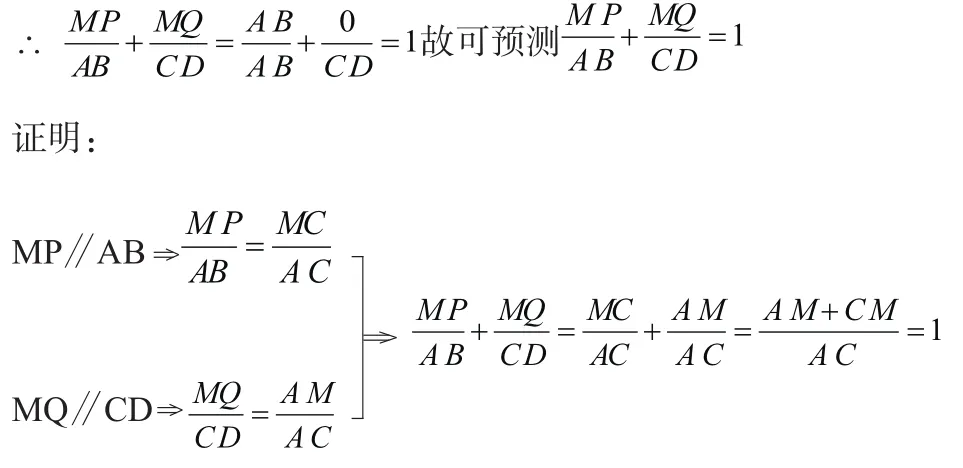
例1 已知四边形ABCD中，∠B＝∠D＝90º，M为AC上任意一点，且MP⊥BC，MQ⊥AD，求证：为定值。

分析：因M是AC上的动点，若M运动到AC的边界位置A（或C）点，则有PM＝AB，MQ＝0

例2 半径分别为R和r的两个圆⊙O1与⊙O2相交于A、B两点，求证：S1－S2为定值。

分析：当⊙O1与⊙O2的交点A、B重合时，即两圆外切，这时S1＝S⊙O1，S2＝S⊙O2此时定值为两圆面积之差，故可预测。S1－S2=π（R2－r2）

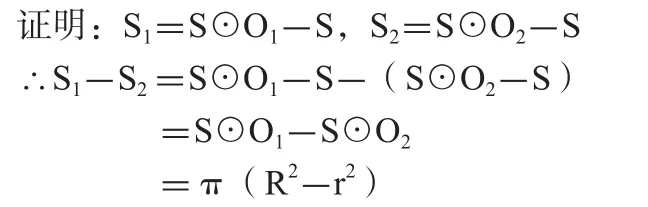
二、从图形的特殊形状求定值。

例3 已知OA、OB是⊙O的半径，AD⊥OB于D，DC⊥AB于C。求证：OC2+CD2为定值。

分析：当△AOB为正三角形时，AD为OB上的中线，设OA=R，则有

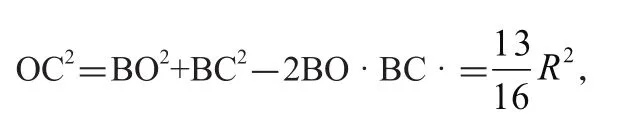
因此可以预测OC2+DC2＝R2

证明：如图由射影定理可得

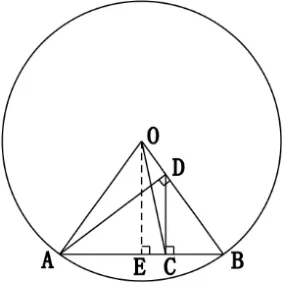
例4 已知⊙O的内接四边形ABCD的对角线AC⊥BD于E，求证：AD2+BC2＝AB2+CD2＝定值。

分析：若E点与圆心重合，则四边形ABCD为正方形，设⊙O的半径为R，则有AB＝BC＝CD＝DA＝R，因此可预测AD2+BC2＝AB2+CD2＝4R2

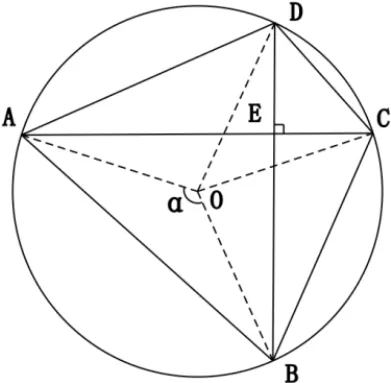
证明：连结OA、OB、OC、OD，设∠AOB＝α

证图形中角的三角函数值为定值，常构建直角三角形，将角的三角函数转化成两条线段的比，进而利用平面几何的有关定理，使问题得到解决。

例5 两个同心圆的半径之比为1:2，大圆的直径AD顺次交小圆于B、C，P为小圆上任一点，设∠APB＝α，∠CPD＝β，求证：·为定值。

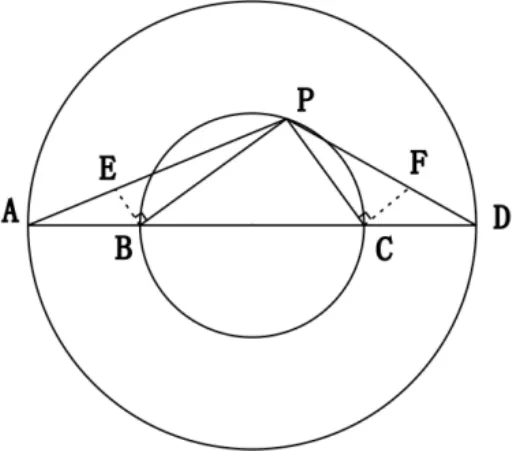
证明：过点B作BE⊥PB交AP于E，过点C作CF⊥PC交PD于F

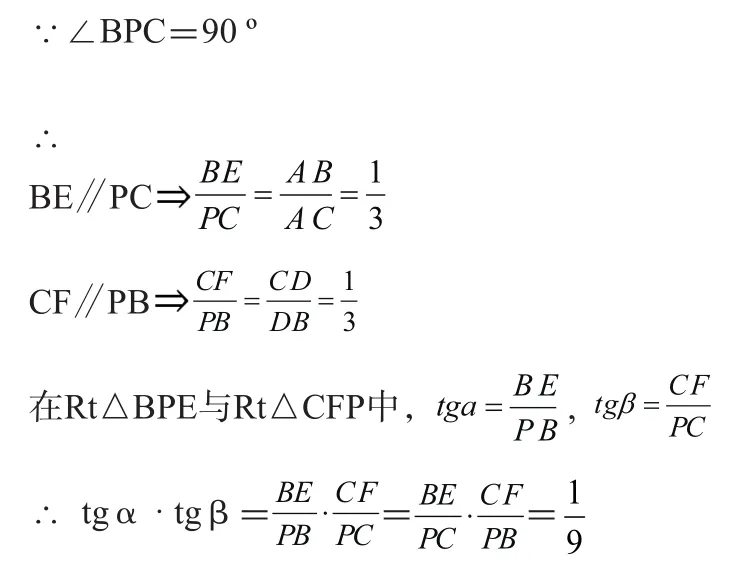
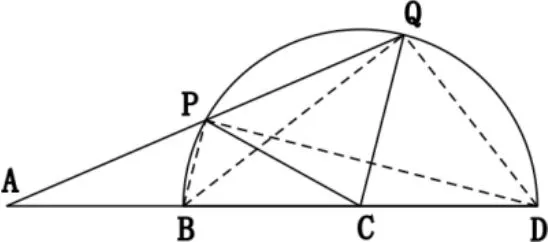
例6 已知B、C把线段AD三等分，以BD为直径作半圆，过点A作半圆的割线APQ，求证：为定值。