基于高斯分布的尾流模型研究*

（作者单位：张忠伟：国网新疆乌鲁木齐供电公司；姚秀萍，常喜强：新疆电力调度控制中心；王海云：教育部可再生能源发电与并网控制工程技术研究中心）

随着人类工业快速发展和人口不断增长，整个社会对能源的需求越来越大，而这种不可再生能源（像煤炭、石油、天然气）用一点就少一点，最终人类将要面对能源短缺的问题；并且开发和消费化石能源带来了诸多方面的矛盾，像破坏原有生态、产生温室效应给人类生产和生活带来严重的威胁，人类开始将视线转向可再生和清洁能源的开发和利用上。在我们所依赖生存的环境中，风能是一种源源不断储藏庞大的洁净能源。风电场的自然来流风流过上游风电机组后，上游风电机组吸收部分风能，带动上游风电机组机轮的转子转动将风能改变为机械能。当到达下游风电机组时，风的速度下降，引起下游风电机组产生的电量减少。并且在风电场中风电机组的间距越小，尾流效应就越明显，可以利用的风能就越少。为了更好、更方便、更经济地做研究，研究学者提出通过数学建模来模拟实际的问题，并且该方法在很多领域都有应用。数值模拟这种简单、有效、经济的预估计方法在科研探索的道路上起着至关重要的作用。

目前在风工程项目中普遍采用的Jensen模型具有结构简单、对计算机的性能要求不高的优点。但使用中发现Jensen尾流模型与真实流场存在一定误差，并且该模型过于粗略，计算精度有限。研究模型认为尾流区域的速率分布形态为流向风电机组距离的函数，在尾流横截面上速度呈现常数分布，和实际流场的真实情况是不符合的。本文根据真实流场中径向速度呈现高斯函数分布和多项式分布，提出一种拟合径向分布的高斯模型分布。并将其与实测值及其他模型计算值进行比较。结果表明，本研究提出的高斯尾流模型能够更加合理准确地描述风电场尾流效应，对风电场微观选址和风电机组布局优化具有指导意义。

尾流模型的建立

一、半经验模型及改进Jensen模型

Jensen模型普遍应用于平坦地形上的风电机组，该模型不探讨湍流效应，模型简单、计算方便。该模型假设：（1）尾流开端的范围是风电机组风轮直径；（2）尾流半径变化呈线性关系；（3）尾流区域横截面各个点上的速率是相同的。尾流模型如图1所示。

图1中，x是下游距风电机组的距离，u是来流风速流经轮毂高度处的风速，v0是上游来流风速，r0是风电机组叶片半径，v、r分别为下游x位置处的风电机组轮毂处的风速与尾流横切面半径。由质量守恒得：

Jensen 模型假设尾流区域横截面的半径遵循一次函数，则尾流半径表示为：

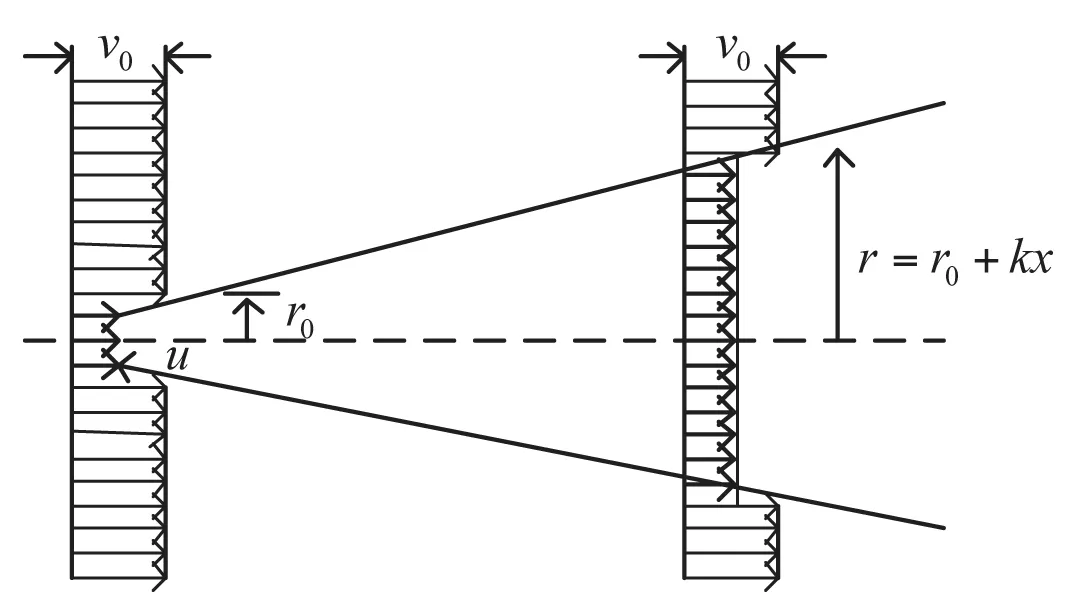
图1 Jensen尾流模型

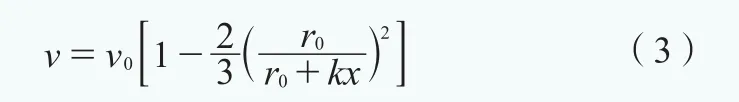
式中a为轴流诱导因数，和风电机组推力系数有关系。将公式（4）带入公式（1）和公式（2），得到改进后的Jensen模型为：

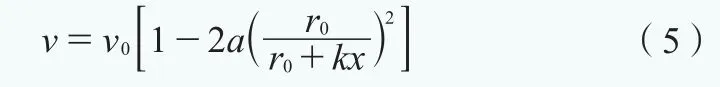
轴流诱导因子a可表示为：

式中CT为风电机组推力系数。

一般k的计算可表示为：

式中z表示风电机组轮毂处的高度，z0为风电场周围地表不光滑度。

二、Jensen尾流模型高斯化

根据Jensen尾流模型演算过程我们可以看出，认为尾流区域的速率分布形态为流向距离x的函数并在尾流截面处的速率为常数，即取值为尾流中心线上的平均风速，属于一维模型。然而大量的实验和数值模拟显示，尾流速度在尾流横截面上的假设与实际尾流流场不符，而且尾流速率在横切面处的速度分布呈现为高斯和多项式形态，针对Jensen模型的缺陷本文提出高斯分布的尾流模型，模型如图2所示。通过尾流速度在尾流横截面呈现为高斯分布，提出选用高斯分布函数拟合尾流速度在径向上的分布，使尾流模型更加接近实际流场。

对尾流场做出假设：1.尾流初始半径为风电机组半径；2.尾流区域的速度呈现非线性分布；3.在风电机组下游位置x处的尾流呈现高斯分布。

风电机组尾流模型如图2所示，假定所选取的流场中不存在粘性剪切力的作用并且是定常的，图中v0、v分别表示无限远处的来流风速、距离为下游位置x处尾流速度。r0和r分别表示风电机组风轮半径和位于风电机组下游x位置处的尾流半径。

建立三维坐标系，x方向表示风的来流方向，y方向表示尾流横切面的水平方向，z方向表示尾流横切面的垂直方向，Δv表示尾流横切面的速度折减。若控制体中因速度折减引起的空气质量流量的损失值与总空气质量流量之间的比值可以表示为：

由尾流横切面速度折减呈现高斯分布可得：

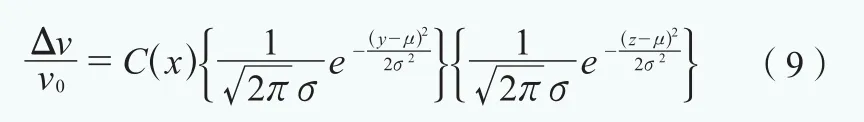
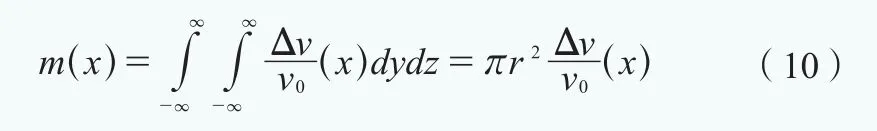
由式（10）、（11）式可知线性扩张模型的质量损失和高斯模型的质量损失相等，可得：

将（8）代入（9）式可得：

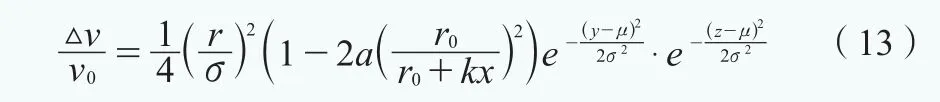
根据高斯分布图像关于期望值对称的特点，则μ＝0，使用（-2σ，2σ）为高斯二维模型的有效分布范围，则高斯分布有效面积为95.446%，因此可得2σ＝r。

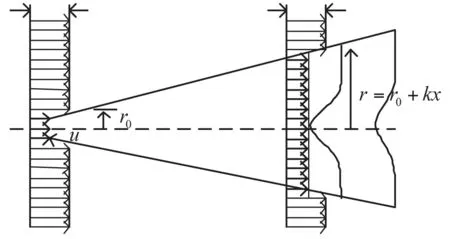
图2 高斯模型

不考虑风切变的影响，在尾流横截面处同一半径内的尾流速度应该相同，所以可以将其转换为二维尾流模型，即：

计算结果

为保证实验的准确性，研究采用Garrad Hassan工程实验模型数据，对修正模型进行计算，并与风洞实验数据做对比。

一、NIBE风电机组参数与尾流比较

为与前人做比较，研究选用NIBE风电机组，NIBE风电机组参数为：风轮直径40m、轮毂处的高度45m、额定功率630kW、切入风速6m/s、切出风速25m/s、额定风速13m/s。并选取和前人相同的来流风速u＝8.5m/s，湍流强度i＝10%，风力发电机组在三个叶尖速比λ＝2.9，λ＝4.0，λ＝5.1对应的推力系数为CT＝0.62，CT＝0.79，CT＝0.85。将上下游风电机组间距为5D、7.5D、10D（D为风轮直径）的风速与前人做的数值模拟计算结果进行对比。

二、中心线轴向速度分布

图3 不同叶尖速比下的轴向速度分布

图4 尖速比2.9时径向速度分布

判断一个尾流预测模型的好坏是看它能否准确计算尾流区域的轴向速度折减。图3中给出了在三种不同叶尖速比下，中心线轴向速度轮廓图。由于Jensen模型在两倍风轮直径后才有效果，因此文章为保持一致性也选用两倍风轮直径后的距离对两种模型进行比较。通过图中曲线变化规律能够发现越靠近前一排风电机组，下游风电机组风速下降得就越明显，相反随着距离的增加这种下降会逐渐减小，并在远后方恢复到来流的风速。并且叶尖速比不断扩大，风电机组推力系数也会随之扩大，相应的尾流效应就越显著。在下游7倍风轮直径之前，Jensen模型和本文的高斯尾流模型都与实际值有较大偏差，这是由于两种模型均未探究风电机组叶片旋转作用。在实际的风洞实验中，风电机组的叶片旋转是不能忽视的，旋转会造成风电机组的下游产生湍流和尾流。

图5 尖速比5.1时径向速度分布

在下游7～16倍风轮直径之间本研究的高斯尾流模型计算数据与实验数据吻合得较好，而Jensen模型总体计算数据偏大。这也说明了本研究数值模拟的合理性。

在下游16倍风轮直径后，Jensen模型演算值仍旧略大于实际值，而本研究提出的模型演算结果和实际值吻合得较好。

三、径向速度分布

图4、图5中分别提供了不同叶尖速比下，位于风电机组不同距离下的风轮径向速率分布。从图中可以直观发现尾流效应，并且随着叶尖速比增大，尾流效应越大。通过比较发现，Jensen模型和本研究提出的高斯尾流模型计算结果在近尾迹区都大于实验结果。这是由于在风电机组下游的一段位置之后，压强不在全部尾流中起全局影响，而是湍流强度和尾在全部流场中起主要作用，在实际状况下，风电机组下游的尾流会慢慢损失，造成能量的减少，以此造成风速减小。在下游风电机组处能够看见高斯尾流模型和实验值较好地吻合。在整个计算结果中高斯尾流模型的计算简单，并且高斯尾流模型在尾流的计算上也有相当的精度，因此高斯尾流模型在工程上的应用有很大的意义：（1）叶尖速比越大风电机组推力系数越大；（2）在径向速度分布上本研究提出的尾流模型在近尾迹区略大于真实值，但在远尾流区和实验值相比表现出较好的拟合性。

结论

研究发现Jensen模型虽然使用较为广泛，但它在尾流横截面方向的速度分布为平均速度，与真实情况有较大误差。推导建立三维高斯尾流模型，发现高斯尾流模型在真实流场中尾流区域的速度分布特性描述更加确切。提出的高斯模型，和Jensen模型以及测得的实际数据比较发现，高斯模型精度较好，计算简单方便更加适用于工程预测。同时也印证了叶尖速比越大，风电机组的推力系数越大。

本文主要以均匀直流条件作研究，并以此提出修正模型。在未来的研究中为了能够更近一步地提高风电场中尾流计算精度，应考虑加入风切变指数和湍流强度这些因素。