清洗机器人倾角传感器信号处理研究

谭 爽,李丽宏*,崔国强(.太原理工大学信息工程学院,太原 03004;.山西万立科技有限公司,太原 03003)

随着我国经济的蓬勃发展,高层建筑不断涌现,玻璃以其良好的采光性、保温性以及实用美观等优点被大量应用于高层建筑的外墙壁。但是由于玻璃幕墙长期暴露在外面,容易蒙尘纳垢,因此需要定期对其进行清洗以保证玻璃的光洁美观。现阶段玻璃幕墙的清洗工作主要依靠人工搭乘吊篮或腰系绳索完成,这种传统的清洗方法劳动强度大,成本高,同时也十分危险[1],因此玻璃幕墙清洗机器人应运而生。利用清洗机器人代替人工进行高楼玻璃幕墙的清洗作业能够有效降低高层建筑的清洗成本,改善工人的劳动环境,提高工作率,具有相当的社会、经济意义和广阔的应用前景[2]。

清洗作业系统是清洗机器人准确完成清洗作业的关键,本文设计的清洗作业系统是利用空间冗余机械臂完成清洗作业。机械臂末端位姿精度是反映清洗机器人性能的一个重要指标,也是确保机器人正常工作、实现高精度工作要求的保证[3]。纵观国内外现有研究,清洗机器人的末端位姿的获取方式主要依赖于倾角传感器完成对各个关节旋转角度的采集,实现对机器人运动末端的精确定位。受户外环境的影响,安装在机器人上的倾角传感器在数据采集过程会受到很多随机因素的干扰,导致测量结果不准确,对实际工程中清洗机器人末端位姿动力学模型的精确完整构建造成困难,严重影响了清洗机器人清洗作业的准确完成,因此如何进行有效的信号处理是目前清洗机器人研究领域的难点问题。

当前已有大量学者对提高倾角传感器测量精度方面进行相关研究,例如:朱月青[4]等为消除温度对倾角传感器的影响,采用BP神经网络法对倾角传感器的输出电压进行数据融合,将传感器的测量精度提高到2%;邵晓敏[5]等通过对倾角传感器输入和输出之间关系进行分析研究,采用最小二乘法对传感器进行信号处理,将倾角传感器输出信号的相对误差控制在1.7%以内;吴俊杰[6]等利用卡尔曼滤波法将倾角传感器在测量过程中的干扰信号滤除,使倾角传感器在10°～20°测量范围内将测量误差控制在2.8%以内;张起朋[7]等根据倾角传感器的测量原理,分别对传感器测量角度在测量无误差和误差下的求解模型,建立含误差项的求解模型,得到倾角传感器角度测量的标定算法,使传感器的测量角度相对误差控制在1.2%以内。

虽然,上述研究均能提高倾角传感器的测量精度,但在实际应用中,倾角传感器在进行信号处理时往往存在操作复杂、精度低、数据处理速度慢等不足,难以获得很好的处理结果。因此,近年来,探索研究多种方法的相互结合实现优势互补成为学者们关注的热点,并且成效显著。基于此,本文提出一种简单可行且精度较高的传感器信号处理方法,利用Savitzky-Golay平滑滤波技术对传感器输出信号进行滤波预处理,再用处理后的传感器信号建立神经网络模型。研究结果表明,该方法有效地减小了误差干扰,使传感器信号的测量精度提高到0.91%,为清洗机器人准确完成清洗作业提供了技术借鉴。

图1 清洗作业系统结构图

1 清洗机器人清洗作业系统原理

清洗机器人主要由攀爬移动控制系统和清洗作业系统两部分组成,其中,攀爬移动控制系统主要通过四肢完成攀爬移动,清洗作业系统主要通过清洗臂完成清洗作业。

清洗作业系统的结构主要包括大臂、小臂、底座和清洗装置,其系统结构图如图1所示。

清洗机器人清洗作业系统中的倾角传感器如图2 所示,其敏感元件为硅微敏感元件。倾角传感器的内部存在一个对加速度敏感的质量块,质量块通过悬臂簧片(具有弹性)固定在敏感器壳体上,且在质量块的上方和下方有一对电极板,两个电极板分别与质量块形成1个相等的电容,当倾角传感器发生角度变化时,惯性力使质量块产生位移,使电极板与质量块之间的间距发生变化,从而引起电容量发生变化,根据电容量的变化值即可得到变化的角度值。

图2 倾角传感器

清洗机器人在清洗作业过程中,通过采集安装在大臂、小臂上的倾角传感器获得清洗臂各个关节的旋转角度,并在控制器中对采集到的倾角传感器数据进行信号处理从而获得清洗臂各个关节的角度,建立运动学方程实现对清洗臂末端的准确定位。系统原理框图如图3所示。

图3 系统原理框图

在实际测量过程中,由于机器人操作环境为户外,所以安装在清洗臂上的倾角传感器在数据采集过程会受到很多随机因素的干扰,导致测量结果不准确,此外,清洗作业系统在长时间工作后,由于受传感器输出信号的误差累积量的影响,清洗臂末端的精度将会受到严重影响,导致清洗作业系统无法正常完成清洗作业,因此本文通过Savitzky-Golay平滑滤波技术对倾角传感器进行滤波预处理得到较准确的传感器输出数字信号,并在此基础上建立神经网络模型,提高传感器的测量精度,从而提高清洗臂末端的精度,减少误差,从而保证机器人清洗系统能够准确完成清洗作业。

2 Savitzky-Golay平滑滤波

Savitzky-Golay平滑滤波是由Savitzky A和Golay M提出的一种基于多项式的最小二乘法拟合滤波方法,是一种自适应的迭代算法,这种方法不依赖于输入数据的模型和先验统计特征,而且运算量相对较小,能够平滑噪声数据,消除噪声干扰,适合在线进行[8]。Savitzky-Golay平滑滤波法是通过将待处理数据中某一连续的数据点选用相应的拟合阶次进行最小二乘法多项式拟合,进而将拟合得到的曲线在数据中心点处的取值作为滤波后的数据值,并依此对其他待处理数据,重复此过程,从而达到对所有数据进行滤波的目的[9]。Savitzky-Golay平滑滤波法的具体滤波过程如下:

设x(n)中的一组数据为x(i),i=-M,…,0,…,M通过构造一个p阶多项式fi来拟合x(i),其中,

(1)

则其总的误差平方和E为:

(2)

为使曲线的拟合度最高、拟合误差最小,通过令E对各系数的导数为0,从而达到总的误差平方和E最小[10],即:

因此可得:

(3)

即:

(4)

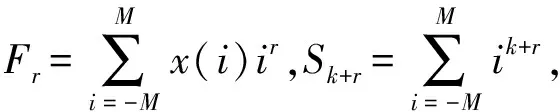
(5)

因此,通过确定M(需要拟合的单边点数)、p(多项式的阶次),则可求出Fr和Sk+r,代入式(5)中即可求出系数a0,a1,…ap从而确定多项式fi,进而求出滤波后的数据值。

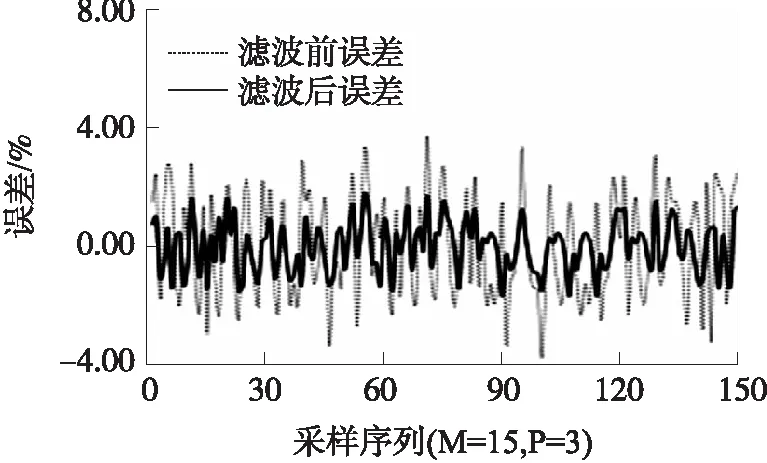
图4 倾角传感器滤波预处理后误差对比图

本文首先通过对传感器采集到原始的数字量信号按照Savitzky-Golay平滑滤波法进行滤波预处理,在拟合单边点数M=15、多项式阶次P=3时处理结果的误差曲线如图4所示。由图4可以看出,Savitzky-Golay平滑滤波法能有效的减少传感器输出误差,提高测量精度,能够为建立神经网络模型提供准确的样本数据。

3 神经网络模型

3.1 BP神经网络原理

BP神经网络是由Rumerlhart D E和McCelland J L及其研究小组于1986年提出来的,又称多层前馈神经网络,具有较强的泛化功能、良好的自我学习能力,它系统的解决了多层神经元网络中权值的变换问题,克服了简单感知不能解决的异或问题[11]。

神经网络算法是一种信息正向传播和误差逆向传播算法,主要由输入层、中间隐含层和输出层三部分组成[12],其结构图如图5所示。训练样本数据通过输入层输入神经网络,通过中间隐含层神经元的多次迭代计算,将运算结果传递到输出层,之后在输出层将运算结果与期望输出值进行比较,若两者之间的误差满足设定误差精度,则结束训练,如果两者之间的误差超过设定的误差精度,神经元会按着减小目标输出与实际输出误差的方向,从输出层出发经由中间隐含层逐层逆向传回至输入层,并在这个过程中修改各层权值。随着训练的不断循环进行,使得网络输出值逐渐向期望输出值逼近[13]。

图5 神经网络结构图

3.2 BP网络在倾角传感器信号处理中的应用

3.2.1 神经网络模型参数设置

①训练函数

BP神经网络的训练函数主要有traingd(梯度下降法)、trainbfg(拟牛顿算法)、traincgb(Plwell-Beale共轭梯度法)和trainlm(Levenberg-Marquardt算法)等函数,其中traingd函数收敛速度慢,对训练结果受学习步长影响大且陷于局部极小,适用于简单网络;trainbfg函数具有单步计算量大和迭代次数少的特点,适用于小型网络;traincgb收敛速度快,适用于较大规模计算;trainlm函数收敛速度快且学习效率高,适用于中等网络[14]。通过分析神经网络模型各个训练函数的优缺点,本文选用具有学习速度较快、单次迭代降低误差幅度大等特点的trainlm算法作为BP神经网络模型的训练函数。

②传递函数

传递函数是连接输入层与隐含层和隐含层与输出层之间的函数,传递函数的不同直接影响着BP神经网络的映射能力。传递函数一般有阈值函数、线性函数、sigmoid函数3种函数形式,由于Sigmoid函数结构简单、非线性映射能力强等优点以及输出值的归一化处理,本文输入层与隐含层之间选取tansig正切sigmoid函数作为传递函数,隐含层与输出层之间选用purelin线性函数作为传递函数,从而实现输入和输出间的非线性映射。

③训练参数设置

神经网络模型训练参数设定如表1所示。

表1 神经网络参数表

3.2.2 神经网络模型的建立

为了提高训练样本迭代运算的速率,提高神经网络模型的运算速度,需要将训练样本数据进行归一化处理,即:将输入变量进行数据标准化,使输入值落在[0～1]区间内,本文选取式(6)对输入变量进行归一化处理[15]:

(6)

式中:yi为归一化处理后样本值,xi为输入样本原始数据,xmin为输入原始样本数据中的最小值,xmax为输入原始样本数据中的最大值。

由于倾角传感器是硅微传感器,其主要材料为薄硅片,利用半导体加工技术制作而成,当传感器所在环境温度变化时,硅材料的弹性模量、拉伸强度、结构热应力以及硅材料杨氏模量等物理特性受温度影响较大[16],从而使硅微传感器的谐振频率、品质因数等参数随温度的变化产生不同的变化,导致倾角传感器产生测量误差,影响倾角测量的准确度。因此可知,倾角传感器的输出角度数据不仅与传感器输出的数字信号有关,还与当前的环境温度有关,因此本文选取倾角传感器采集的数字信号、温度作为模型的输入参数,传感器测量角度值作为输出,即2个输入神经元和1个输出神经元;本文采用节点渐增法来确定隐含层神经元的数量,即:先用较少数目的隐含层神经元的数量构成神经网络训练,然后根据训练精度逐渐增加隐含层神经元的个数,直到达到设定的训练精度为止,经过多次训练,当隐含层神经元的数量为11时,达到设定的训练精度。因此本文建立拓扑结构为2∶11∶1的神经网络模型。

3.2.3 神经网络模型结构

本文在MATLAB 7.0环境下建立如下式所示的神经网络模型结构:

net=newff(minmax(traininput),[11,1],{‘tansig’,‘purelin’},‘trainlm’)

(7)

式中:net为本文建立的BP神经网络模型;newff为在MATLAB7.0中生成的BP神经网络函数;minmax()用以求解输入样本参数的最小值和最大值;[11,1]中“11”代表中间隐含层的神经元个数,“1”代表输出层神经元个数;{‘tansig’,‘purelin’}分别表示输入层到隐含层和隐含层到输出层的传递函数;‘trainlm’如前文所述表示神经网络的训练函数。

γ=purelin{iw2[tan sig(iw1M+b1)]+b2}

(8)

式中:γ是传感器输出的角度值;iw1、iw2分别是所建神经网络模型输入层到隐含层的权值、隐含层到输出层的权值;b1、b2分别是网络模型输入层到隐含层的阈值、隐含层到输出层的阈值;式(8)中M=[μ,ω],μ表示经过滤波处理后的数字信号,ω表示温度。

4 算法验证及分析

将倾角传感器固定在三轴精密转台(惯性器件标定工具)上放入调温箱中对传感器进行数据采集,其中,转台产生的标准角度值作为度量倾角传感器测量数据精度的真实值。通过数据采集得到包含温度和传感器输出数字信号的150组数据,然后将采集到的传感器数字信号经过Savitzky-Golay平滑滤波预处理得到滤波后的数字信号,再从150组包含温度和滤波后传感器数字信号的样本数据中随机选取120组数据建立神经网络模型,剩余30组样本数据用来检测所建模型的精度。建立的神经网络模型的误差收敛曲线如图6所示。

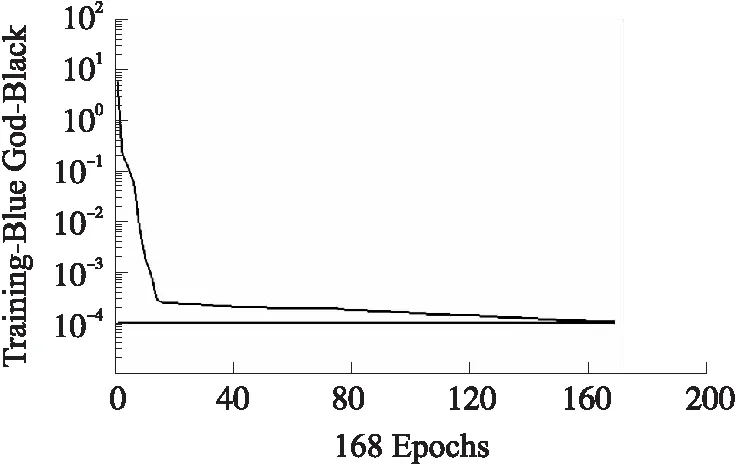
图6 神经网络误差收敛曲线

由图6可以看出,当训练步数为168步时,训练精度达到0.000 099 88,满足训练目标精度0.000 1的要求,收敛速度较快。

此外,本文还将30组检验样本分别通过未加任何算法处理的传感器采集的原始数据相对误差、经过Savitzky-Golay平滑滤波处理数据的相对误差以及Savitzky-Golay和神经网络组合模型处理的相对误差进行比较,误差比较结果如表2所示。

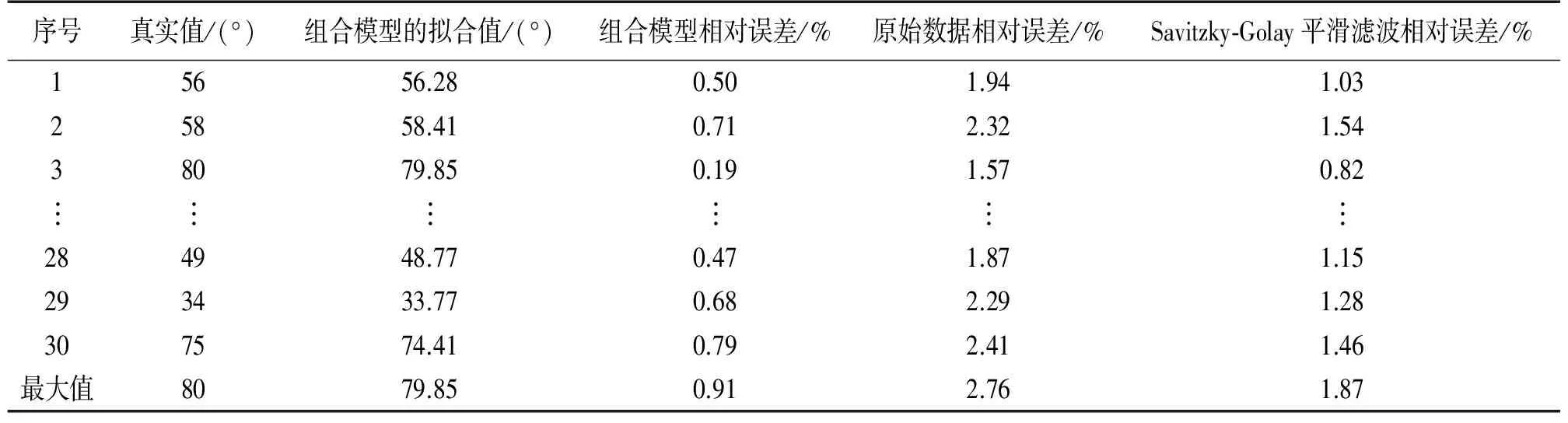
表2 检验样本数据误差比较

注:相对误差是指传感器测量的角度值与转台产生的标准角度(即真实值)进行对比得到的相对误差。

由表2可以看出,Savitzky-Golay和神经网络组合模型较未经任何算法处理的传感器测量的原始数据以及单一采用Savitzky-Golay平滑滤波技术处理的传感器数据精度都高,由此可见将Savitzky-Golay平滑滤波技术和神经网络算法结合能够有效地提高传感器的测量精度,可为清洗机器人准确完成清洗作业提供强有力的理论与技术支撑。

5 结论

本文通过将Savitzky-Golay平滑滤波技术和BP神经网络相结合,建立以温度、滤波后传感器数据作为输入变量的神经网络模型,将清洗机器人倾角传感器输出信号的测量误差控制在0.91%以内,大幅度提升了传感器输出数据的测量精度,为清洗机器人准确完成清洗作业提供了一种新思路。

另外,考虑到BP神经网络容易陷入过拟合的缺陷,应在后续研究中加强对倾角传感器输出信号影响因子的机理分析,合理确定输入因子,优化神经网络的微观模型结构以进一步提高模型精度。