基于组合预测算法的光栅信号新细分方法研究*

陈自然,李 钢,赵 建,田 伟(重庆理工大学机械检测技术与装备教育部工程研究中心,时栅传感及先进检测技术重庆市重点实验室,重庆 400054)

机床工业是国民经济的基础产业,其发展水平是衡量国家工业化程度的重要标志。大力发展数控机床产业是国家工业化道路上的必经之路。数控机床作为现代先进制造的主流加工设备,已成为国际制造业和国防工业竞争的焦点。数控机床的不断发展对机床关键功能部件提出了更高的要求。目前市场上主要采用光栅传感器作为机床位置检测与反馈部件,其测量精度直接关系系统主机性能[1-3]。

光栅测量的本质是对莫尔条纹的计数实现位移测量。栅距精度决定测量的精度,栅距的密度决定测量分辨力,要实现高精度高分辨力测量,就必须要求光栅栅距刻划得又精又密。精密位移测量领域中往往要求在大量程范围内实现高精度、高分辨力测量以解决宏观结构下微细尺度的精密检测与控制。如果通过减小栅距来提高测量分辨力,不仅加工难度大,在工艺上也不易实现。并且光学衍射极限制约了光栅制造工艺向刻划密集方向的发展[4-5]。目前提高位移传感器测量分辨力的主流技术就是引入信号辅助细分手段[6-8]。

根据细分原理的不同,可以将光栅信号的细分方法分为机械细分法、光学细分法、电子学细分法和微处理器细分法。其中光学细分法和机械细分法工艺复杂,成本较高,精度较低,因此应用范围受到限制。而电子细分和微处理器细分所得到的细分信号能直接输入到控制系统实现位置反馈,且原理简单,因此得到广泛的应用。按照对光栅输出信号细分参数的不同,可以将电子学细分法分为幅值型细分法[9-10]、相位型细分法[11]和锁相倍频细分法[12]等。微处理器细分法主要是以处理器为硬件,采用智能算法实现光栅信号细分[13-16]。受光栅光源准直性、光栅刻划误差、机械安装误差等因素影响,光栅输出信号不是标准的正弦和正交信号,其中包含直流电平,两路信号幅值不等,相位不正交及噪声干扰等因素,这些将严重影响光栅细分精度。以上传统光栅信号细分方法对传感器输出的原始信号波形质量要求较高。为了减少原始信号波形失真对光栅细分精度的影响,国内外学者在提高原始信号质量方面做了大量的误差修正方面的研究[17-20]。这些工作复杂、难度大,效果也比较有限。

本文将光栅运动的空间位置和运动时间相关联,充分利用光栅自身制造精度,研究一种光栅信号自适应细分方法及细分误差修正算法,此细分方法与光栅输出信号正弦性无关。

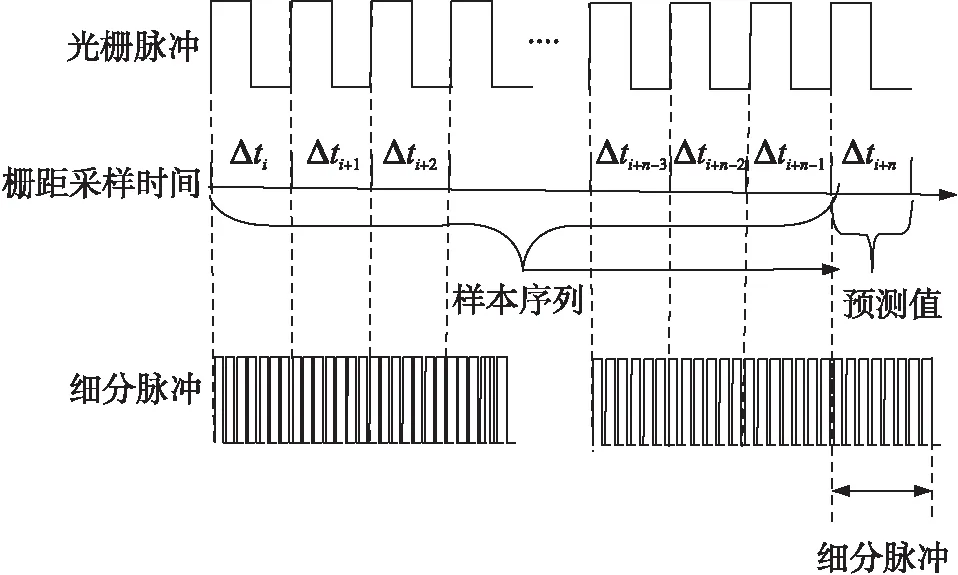
图1 光栅细分原理

1 光栅信号细分原理

光栅在运动过程中,空间位置与运动时间互为映射,利用空间和时间的对应关系,提出一种利用时间基准测量空间的新方法。光栅运动单位栅距触发输出空间脉冲信号,通过采样空间脉冲时间建立运动时间与运动空间之间的映射关系。如图1所示,通过触发生成的栅距采样时间Δti,Δti+1,…Δti+n-1作为序列样本,建立数学模型,预测光栅触发当前栅距的采样时间Δti+n。根据细分倍数,在采样时间Δti+n内由微处理器采用脉宽调制技术(PWM)发出带空间当量的细分脉冲,从而实现光栅信号细分。

2 光栅细分算法研究

由于光栅运动的随机性,在不同的运动状态中,光栅栅距采样时间和空间映射关系也在动态变化,为了减小由于运动状态改变带来的信号细分误差,针对不同运动状态特性,研究采用指数平滑法和灰色算法相结合的组合式预测算法建模,提高光栅信号细分精度。

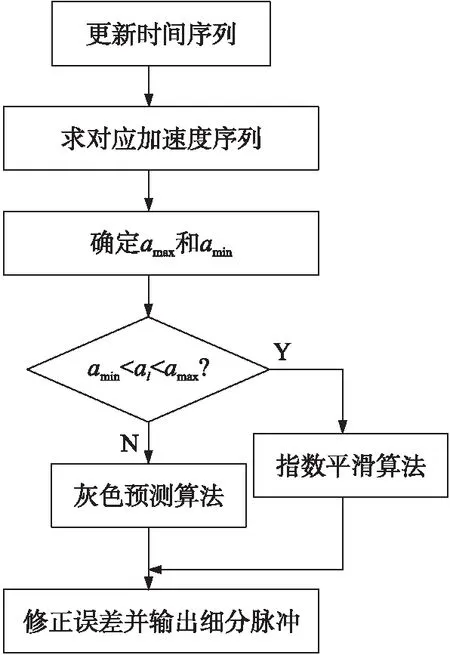
图2 状态判断流程图

2.1 光栅运动状态判断

单位栅距的位移是固定的Δs,处理器系统在单位栅距内采用ARM芯片中定时器的捕获(Capture)单元测量光栅输出信号的脉冲宽度,即实际单位栅距触发的采样时间,能够采样得到时间序列Δti,Δti+1,…Δti+n-1,由于机械系统具有惯性和二阶动态特性,在单位微位移(栅距)范围内可近似认为光栅运动满足连续和平稳性要求,采用式(1)、式(2)可求出两个相邻单位栅距内的光栅运动加速度ai。

(1)

(2)

式中:vi和vi+1分别为第i和i+1个栅距的通过速度。利用式(1)、式(2)可以根据时间序列Δti,Δti+1,…Δti+n-1求出相对应加速度序列(并取绝对值)|ai|,|ai+1|,…|ai+n-2| 并求出加速度序列中的最大值amax与最小值amin。光栅运动状态判断流程图如图2所示。

当加速度的绝对值大于加速度序列中最大值amax或小于最小值amin,对应于变速状态,否则认为光栅运动在平稳状态。

2.2 指数平滑法

指数平滑法常应用于中短期的发展趋势预测。光栅作平稳运动时,由于惯性的作用,光栅运动速度在单位栅距微位移中不会发生骤变,通过每一个栅距触发的采样时间相对稳定,因而采样时间序列的态势具有稳定性和规律性。当前栅距的采样时间量与采样时间样本序列具有较强相关性。因此当光栅在平稳运动状态时,可采用二次指数平滑法进行建模。

首先建立一次指数平滑模型如式(3)所示:

(3)

在一次指数平滑的基础上在一次做平滑处理即得到二次指数平滑模型:

(4)

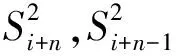
(5)

式中:

(6)

(7)

2.3 灰色算法

当光栅由平稳运动过渡到不平稳运动状态时,在这个阶段数据规律变化较剧烈,研究采用灰色预测算法,利用其在小样本数据中具有较强鲁棒性的特点,建立光栅栅距触发采样时间和运动空间的映射关系。

(8)

式中:时间序列Δt(0)为原始序列,进行一阶累加得到一阶累加序列(9):

(9)

构建灰色预测模型对应的微分方程为式(10):

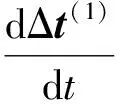
(10)

式中:β为发展灰数,μ为内生控制灰数。简化模型为:

Y=Bα

(11)

(12)

利用最小二乘估计法得到;

(13)

(14)

最后累减得到最后的预测值:

(15)

令k=i+n-1,则预测第i+n个栅距的通过时间为:

(16)

2.4 细分误差修正模型

为了消除信号细分误差累积,保证细分精度,研究预测的栅距触发采样时间与真实采样时间值所构成的误差序列样本之间的相关性,采用马尔科夫修正模型预测当前栅距的采样时间误差,从而修正上述预测算法所带来的时间误差对空间细分误差的影响。

Pt+1=P0[P(1)]t+1

(17)

式(17)是马尔科夫链预测模型,其中P0为初始时刻无条件的概率分布。Pt+1为t+1时刻的概率分布,P(1)为一步转移概率矩阵:

(18)

式中:pij为从i状态转移到j状态的概率。

根据时间预测算法得到的预测结果,计算出预测值与真实值之间的误差,根据指数平滑法与灰色预测算法的特性将误差划分为不同的区间,并构建马尔科夫预测模型,最后对误差进行修正。当确定了当前误差所处的状态区域后,即可得到最后的修正值,最终得到修正后的第i+n个栅距的预测通过时间为Δt:

(19)

式中:δ为当前栅距触发采样时间误差修正值。

3 细分实验研究

为减少机械运动导致的机械振动和环境温度变化给实验带来的影响,研究采用大理石平台搭建所需的实验系统,其中包含两个用于比对实验的HEIDENHAIN公司的36 000线精度为±1″圆光栅ROD880。两个圆光栅采用高弹性联轴节与数控转台同轴安装。以可编程多轴控制器PMAC作为控制核心,采用Kollmorgen直驱电机作为运动部件驱动转台带动两个光栅同步运动。光栅1采用海德汉IBV660B细分盒进行400倍细分,细分后每个脉冲所代表的空间当量为0.09″,光栅2采用组合预测算法的细分方法,由于光栅栅距固定为36″,本实验细分倍数为100,每个细分后脉冲所代表的空间当量为0.36″,细分脉冲采用脉宽调制(PWM)技术发送出去,其脉冲频率和光栅运动速度成正比。将光栅通过海德汉IBV660B细分盒进行400倍细分的脉冲和采用组合预测算法细分的脉冲同步采集计数得到细分误差。

图3 光栅细分实验系统

图4 光栅细分实验结构方框图

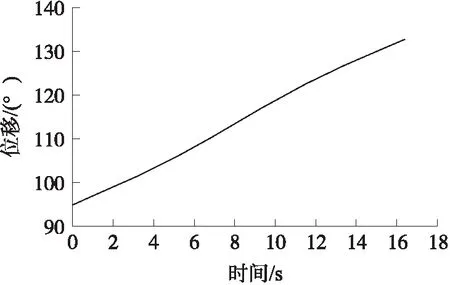
图5 光栅运动时间-位移图

为验证本算法的可行性,图5为光栅在数控转台驱动下角位移运动曲线图,光栅从95.6°运动到132.8°历时16.406 1 s,图6是采用ARM芯片中定时器的捕获(Capture)单元测量光栅输出信号的脉冲宽度,即实际单位栅距触发的采样时间,运动过程分别是平稳运动和非平稳运动两个状态,具体包含低速近似匀速运动(2.0 °/s),匀加速运动,高速近似匀速运动(2.8 °/s),匀减速运动,低速近似匀速运动(2.0 °/s)。

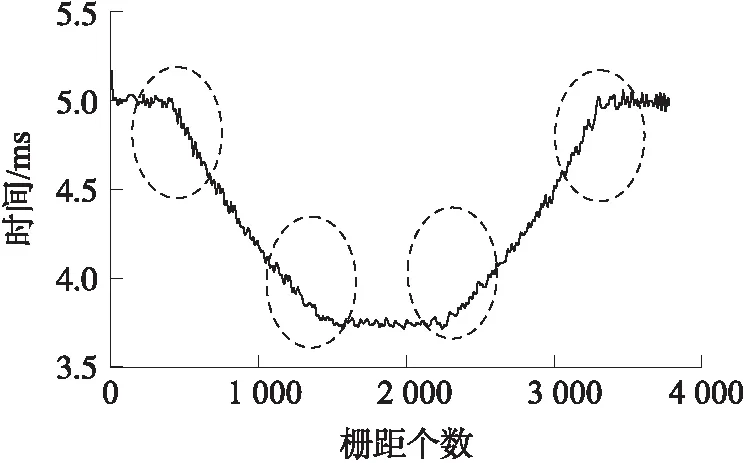
图6 单位栅距运动采样时间

本系统采用的是组合式的预测算法,当光栅作平稳运动(近似匀速、匀加速或减速)时,采用指数平滑法对经过当前栅距的采样时间进行预测,当光栅在运动状态发生改变时(近似匀速与变速运动来回切换的“临界”状态,如图6中圆圈部分所示),采用的是灰色预测算法。

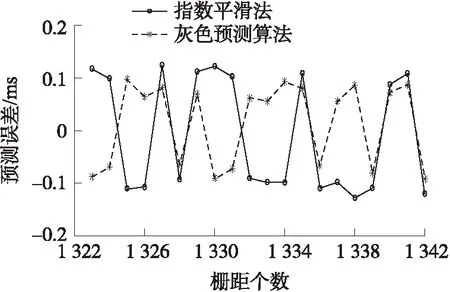
图8 加速到高速近似匀速的预测采样时间误差对比图

为了突出组合预测算法的有效性,做了3组对比实验进行分析。第1组为不平稳状态下的指数平滑法和灰色算法实验数据精度比较,即图6中圆圈部分所示的近似匀速与变速运动切换的“临界”状态条件下栅距触发采样时间的预测精度对比分析,具体数据如图7～图10所示。

图7 低速近似匀速到加速的预测采样时间误差对比图

图9 高速近似匀速到匀减速的预测采样时间误差对比图

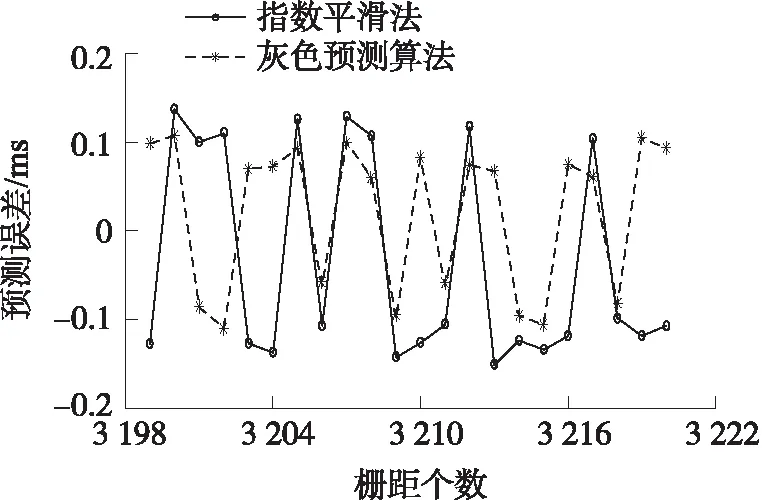
图10 匀减速到低速近似匀速的预测采样时间误差对比图

由图7～图10可知,在“临界”状态,灰色预测算法能够将光栅栅距触发采样的时间误差控制在±0.11 ms,对应的细分误差为±0.75″,而采用指数平滑法只能将光栅栅距采样时间误差控制在±0.15 ms,对应的细分误差为±1.01″。并且相较于指数平滑法,灰色预测算法在“临界”区,预测误差更加平稳。因此当光栅运动处于“临界”状态时采用灰色预测算法能够减少预测误差。

图11 指数平滑法与组合式预测算法细分误差对比图

第2组实验是采用指数平滑法、灰色算法与两者相结合的组合预测算法对整个运动过程的光栅栅距采样时间值进行预测分析,对比各细分误差效果,实验数据如图11和图12所示。灰色预测算法对应的采样时间误差±0.13 ms,对应的细分误差为±0.92″,而采用指数平滑法对应的采样时间误差±0.17 ms,对应的细分误差为±1.06″。相对于在光栅整个的运动过程中使用单一的预测算法,组合式的预测算法误差较小为±0.12 ms,对应的细分误差为±0.79″。

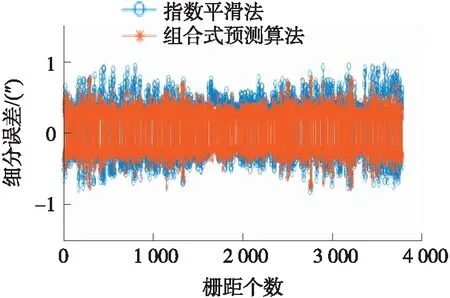
图12 灰色算法与组合式预测算法细分误差对比图

第3组是采样时间误差修正前后的光栅信号细分误差对比实验。图13是马尔科夫修正前后的预测误差对比图,没修正前采样时间误差为±0.12 ms,对应的细分误差为±0.79″,修正后采样时间误差为0.081 ms,对应的细分误差为±0.56″,马尔科夫修正模型能够对运动过程中的预测采样时间误差进行修正。

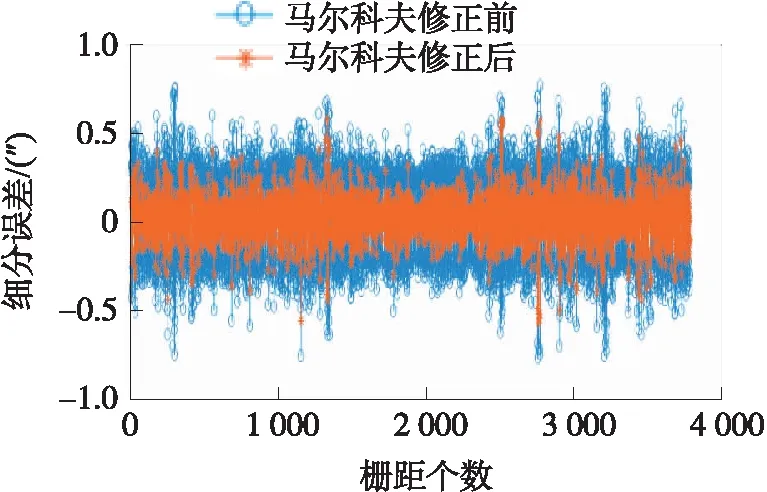
图13 修正前后细分误差对比图

4 结论

①在分析不同运动状态特性的基础上,研究采用简单迭代算法,充分利用指数平滑法的线性特征和灰色算法的鲁棒性,综合平衡算法的实时性和预测精度,提出一种光栅信号自适应细分新方法,实现光栅信号细分,尽量减小由于加速度波动给信号细分精度带来的影响。

②为消除误差累计,提高光栅信号细分精度,研究采用马尔科夫修正模型处理预测值与真实值的误差组成的误差序列,通过分析样本之间的相关性,预测当前栅距的采样时间误差,通过修正采样时间值实现提高光栅信号细分精度的目的。

③本文充分利用运动时间和运动空间的映射关系,提出一种利用时间基准测量空间的新方法。此方法突破了传统的光栅细分方法对光栅输出信号波形质量高要求的局限,最大限度利用光栅自身制造精度,将传统光栅信号对细分电路的硬件高要求用软件算法来灵活处理,成本低,精度高,并可适用于磁栅、感应同步器等传感器中,在精密测量领域具有重要通用性。