一种印刷机械故障标识检测新方法的研究

侯和平, 徐卓飞, 刘 凯, 赵庆海(.西安理工大学 印刷包装与数字媒体学院, 陕西 西安 70048; .西安理工大学 机械与精密仪器工程学院, 陕西 西安 70048)

印刷机械是将印版表面上的图文信息转移并牢固地附着在承印物表面上完成大规模复制的机器。由于印刷机械是一种结构复杂、精度极高、运转高速、多介质耦合的设备,生产过程中一旦出现故障将在短时间内产生大量废品,浪费大量纸张、油墨、部分昂贵包装材料等。印刷品作为印刷机械的产品,由各印刷色组单元按照印刷工艺的顺序精确叠印而成,各机构的运行状态以油墨为载体记录在印刷画面之中。通过对印刷画面的检测,提取有关的特征参数,反演印刷机械关键机构的工作状态,进而判断印刷机械故障是当前印刷机械故障诊断一种新的研究方法。与传统机械故障诊断方法相比,该方法将印刷故障检测标识作为传感器,与其他印刷内容放在一起进行印刷,通过检查印完的样品,提取标识的特征,分析特征的变化来推断机构的运行状态[1]。

常用印刷故障检测标识见图1,(a)为多色套印检测标识,(b)为传纸和输纸机构运动状态的检测标识,(c)为印刷机滚筒与墨辊压力以及滚筒传动齿轮振动的检测标识。这些印刷机械故障标识都是直线的不同组合,通过检测直线间距以及宽度的变化,与预设值进行比较就可判断机构是否出现运行故障[2]。因此,能够准确快速识别、定位标识中的直线并提取相应的特征,是实现印刷及印刷机械故障准确判断与预测的关键。

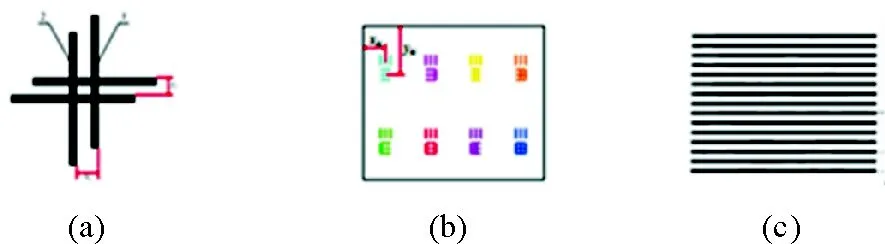
图1 各种印刷及印刷机械故障检测标识Fig.1 Kinds of printing inspection marks

对于直线的检测,其基本思路是:先对图像进行边缘检测,即提取图像中的边缘点或特征点集合,然后利用相关算法识别集合中的直线[3-4]。边缘检测即寻找图像灰度值阶跃性变化或者屋顶状变化区域的边缘。算法的好坏、结果的可靠性和正确性将对提取轮廓的精度、系统性能和系统对图像的理解产生直接影响。文献[4]提出了一种基于Hough变换和最小二乘法结合的直线检测方法,应用于套印标识的检测;文献[5]采用Laplace、Roberts、Canny、Prewitt和Sobel算子等实现边缘检测,但直线周围灰度的变化为阶跃状,包含灰度急剧上升和下降,会出现双边缘现象,导致后续边缘定位出现偏差;文献[6]提出了基于Radon变换与灰度投影积分方法的矩形检测,该方法保证了矩形检测的准确性,提高了矩形检测的速度,但是应用于自动检测时的计算速度比较慢。OPTA算法(One-Pass Thinning Algorithm)细化比较彻底但在纹线的水平和垂直方向会产生较多毛刺,且在分叉点处存在不是单像素宽的问题;快速细化算法(Quick Thinning Algorithm)运行速度快,纹线光滑无毛刺,但不是单像素宽[7]。

本文提出了一种结合快速细化算法和最小二乘法拟合的快速直线检测方法,以用于印刷画面中故障标识的直线检测,为印刷偏差自动计算提供支撑。该方法具备运行速度快、精度高的特点,符合实际生产的要求。

1 标识直线检测方法

印刷故障标识图案由相互垂直的直线组成,直线的宽度和间距在设计时有相应的规定,如传纸和输纸机构运动状态的检测标识直线宽度设定为0.4 mm,直线的间距为0.4 mm。完成标识检测的主要内容包括:利用ZS细化算法实现直线单像素宽的细化[8],并采用最小二乘法对图像中最长直线进行线性拟合得到图像倾斜角,对倾斜校正之后的图像进行水平和垂直方向的灰度积分投影,完成直线的快速检测[9-11]。主要步骤如下。

1) 对待检测图像进行预处理(灰度化,二值化)。

2) 对预处理图像执行细化算法。

3) 最小二乘法拟合直线得到倾斜角,校正图像倾斜。

4) 运用灰度积分投影方法求取图像在水平和垂直方向的投影图,并定位直线的位置。其检测流程图见图2。

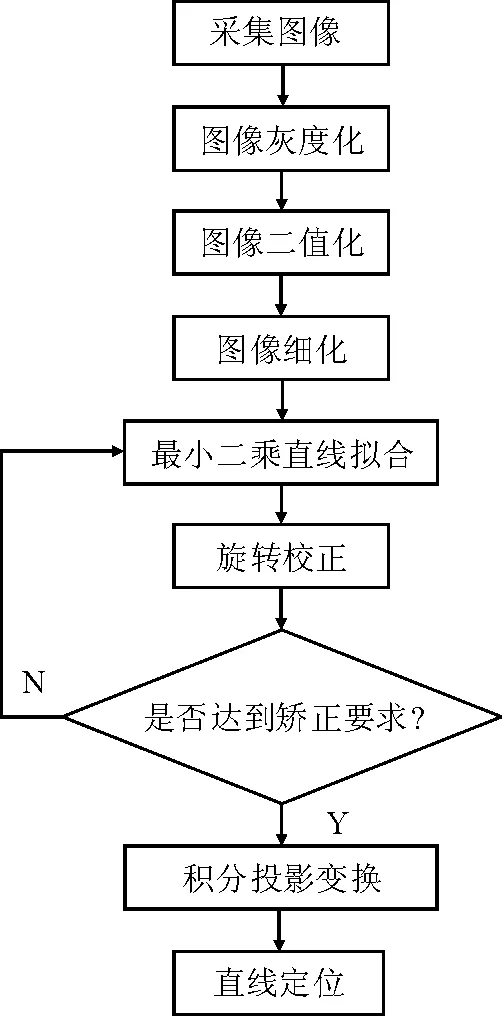
图2 检测流程图Fig.2 The flow chart of detection

1.1 边缘检测

ZS算法作为8邻接、并行细化算法迭代次数少,运行速度快,对直线、T行交叉和拐角的处理能精确地与原图像保持一致,是目前应用最为广泛的算法之一[12]。图3为8邻域示意图,物体轮廓点及前景点的值为1,图像背景点的值为0。

图3 8邻域示意图Fig.3 8-neighbood schematic diagram

对于值为1的任意像素点P1,采用ZS算法的细化过程如下。

Step1 若P1点8邻域满足:①2≤N(p1)≤6,②S(p1)=1,③p2×p4×p6=0,④p4×p6×p8=0,则将P1点标记为待删除,等到本次扫描结束后,删除标记的像素,即令p1=0。其中,N(p1)表示P1像素8邻域中非0点的个数;S(p1)表示P1像素8邻域中以P2、P3、…、P9为序时,像素值由0变1的次数。

Step2 若P1点同时满足Step1中的①和②以及条件⑤p2×p4×p8=0和条件⑥p2×p6×p8=0,标记P1为待删除点。

Step3 重复上述Step1和Step2操作,直到原图像中没有满足标记条件的像素点,此时剩下的像素点组成边界的骨架,细化过程结束,完成直线的边缘检测。

1.2 线性拟合

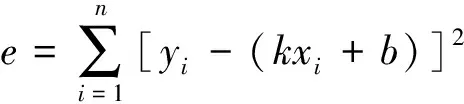
Step1 由于拟合直线需要尽可能靠近或通过所有点,即求偏差平方和的极值,则必然满足对各变量的偏导数等于0,即对目标函数e求偏导数,结果如下:

(1)

Step2 整理合并括号内各项,并分离k和b,结果如下:

(2)

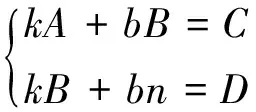
(3)

并求得k和b的值如下:

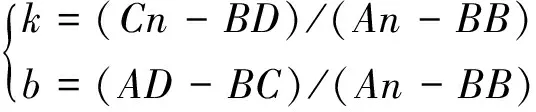
(4)

Step4 拟合得到直线的斜率k,同时倾斜角θ的范围为0°≤θ<180°,则倾斜角θ的值如下:

θ=kπ+arctan(θ) (k=0,1)

(5)

以上是最小二乘法拟合直线的常用方法,该直线拟合方法能快速、高精度确定图像中直线的方程,有利于提高图像倾斜校正的精度。

由于纸张位置变化以及收纸机构振动等原因,拟合后的直线通常有一定的倾斜,需要对标识图像可进行旋转校正。通过简单的坐标旋转变换即可实现旋转校正:

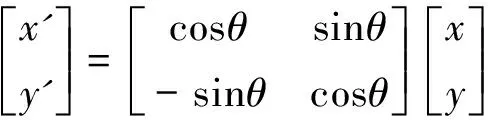
(6)

式中,(x,y)为旋转前的图像坐标,(x',y')为旋转后的图像坐标。

1.3 直线定位

倾斜校正完成后的直线,要进行定位,以便确定直线间的距离,定位方法运用积分投影法[11-13]。当图像某一行像素灰度值发生变化时,水平积分投影值会体现出相应的变化;同理垂直积分投影值反映某一列像素灰度值的变化情况。假设f(x,y)是像素点(x,y)处的灰度值,则水平方向积分投影Sh(x)和垂直方向积分投影Sv(y)的定义如下:

(7)

式中:n为图像一行所有的像素点数;m为图像一列所有的像素点数。

由上述公式可知,水平或者垂直积分投影是对图像中一行或一列像素点灰度值的累加及显示。因此,投影图像中灰度值的极值即原图中直线的位置,同时极坐标系下的投影能够确保算法具有旋转不变性,提高定位精度,降低错误定位率。

图4所示为垂直和水平积分投影效果图,图中直线极值即为采集图像中直线的位置,得出直线位置如表1所示。

表1 标识1中直线位置Tab.1 Location of straight lines in the first logo

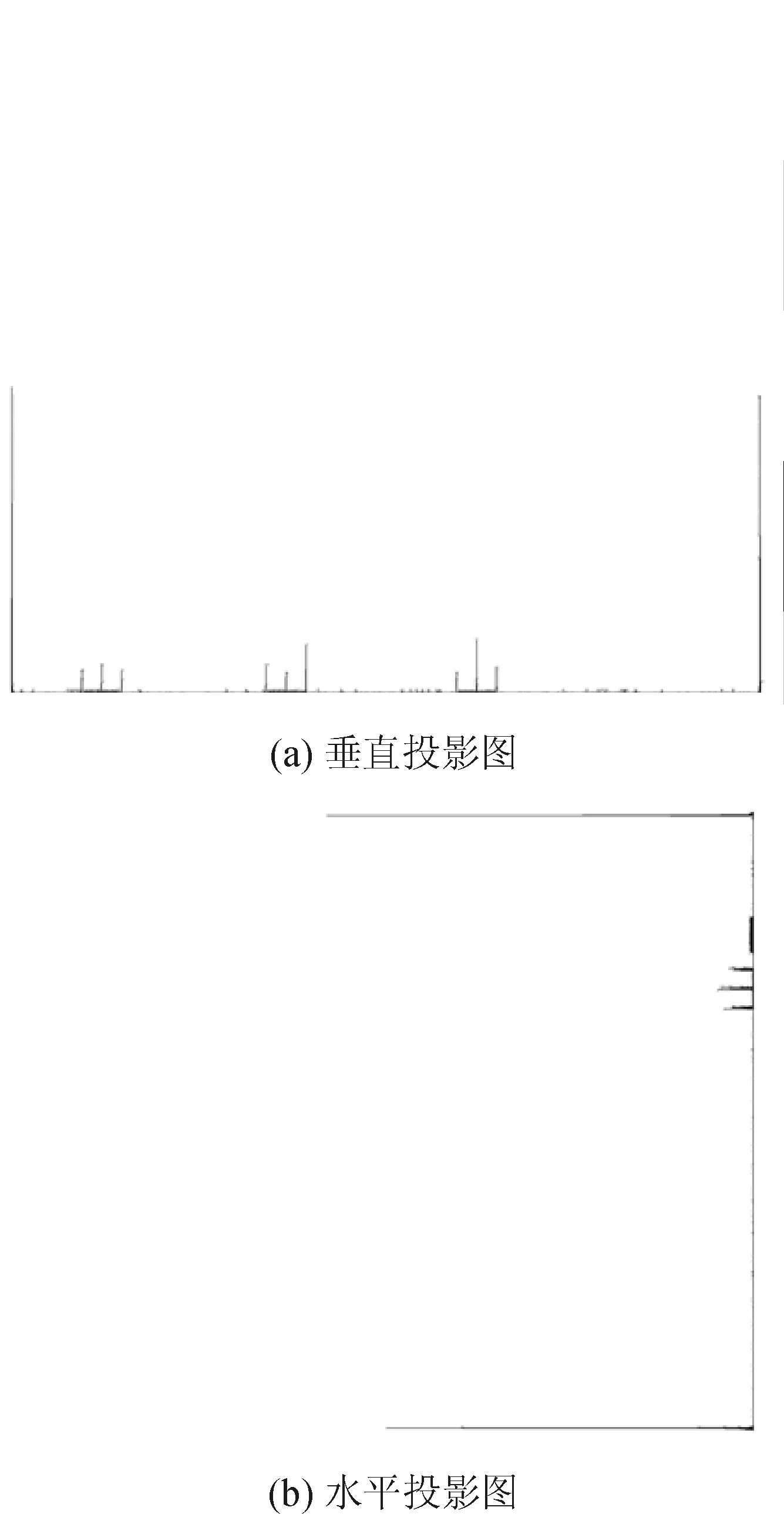
图4 灰度积分投影图Fig.4 Image of gray integral projection

2 实验及算法对比

2.1 实验描述及方案

本实验将印刷传纸及输纸故障检测标识与其他印刷图像一起制版,置于印版的咬口部位,并将制作好的印版安装在PZ650胶印机上,将图像采集装置放置在胶印机的收纸位置,调节好印刷机的各种印刷参数,开机进行印刷。实验场景见图5。

图5 实验现场图Fig.5 Experimental platform

本次实验使用的仪器有:计算机直接制版机Trend setter 800Ⅱ;型号为W-PTP-850C的冲版机;光华PZ1650单张纸印刷机;最小刻度为0.005 mm的MG10081-2150X读数显微镜;由面阵CCD相机ECO655、远心镜头TEC-M55、宽条型光源JK-L20032W、支架以及外部触发器搭建而成的图像采集存储系统、计算机和图像特征提取软件模块。

2.2 实验采集处理结果

在印刷稳定、印刷速度3 600 r/h的速度下进行印刷,采集印刷故障标识,并将印刷故障标识存储在计算机中。处理过程见图6,连续采集100张印刷样张,运用本文算法与Canny算法进行检测,并将检测的结果对比,比较结果如表2所示。结果表明均值更接近理论值,标准差变小,数据集的一致程度更好,即直线定位精度更高。

表2 本文算法与Canny算法对比Tab.2 Contrast of Canny algorithm with this algorithm

图6 故障标识检测及处理Fig.6 The detection and processing of fault identity

3 结 论

通过对印刷标识的检测反演印刷机械重点机构的运行状态是一种全新的印刷机械故障诊断的方法,其关键是能够准确、快速提取印刷故障标识的特征参数。本文提出了一种结合快速细化算法和最小二乘法拟合的快速直线检测方法,应用于印刷画面的直线检测,通过在机印刷提取印刷标识。主要的结论如下。

1) 分析了不同的印刷故障标识,找出了不同印刷故障标识的主要特征。

2) 通过ZS算法与最小二乘法实现了直线的快速检测。

3) 通过对比实验证明了本文计算的均值更接近理论值,标准差变小,数据集的一致程度更好,直线定位精度更高。

4) 为印刷故障标识在机识别与特征提取提供了支撑。