崇寿寺砖塔结构地震损伤数值分析

司建辉, 李 凯, 卢俊龙, 陈 策, 李嘉怿(.西安理工大学 土木建筑工程学院, 陕西 西安 70048; .西安建筑科技大学 土木工程学院, 陕西 西安 70055)

我国历史悠久,现存古建筑承载了辉煌灿烂的古代文明,古塔是古建筑中的高层建筑,体现了古代高超的建筑技艺。历史上曾出现多次建塔高峰期,特别是唐宋时期建造了大量保存至今的砖石塔,因建造年代久远且多次遭受自然及人为的破坏致使结构存在损伤,迫切需要进行有效的保护。同时我国也是一个地震多发的国家,残损古塔在遭受地震作用后,既有损伤累积将导致结构发生破坏,成为砖石古塔结构安全的主要威胁。通过进行古塔结构地震损伤分析,可实现科学评估现存砖石古塔的抗震性能,以便对其进行合理有效的加固保护。

在砖石古塔结构损伤及抗震的相关研究中,邱洪兴[1-2],曹双寅[3]等基于结构损伤识别理论,对江苏省常熟市崇教兴福寺塔进行了结构可靠性鉴定,探讨了结构损伤识别与诊断的系统方法。袁建力等[4-6]结合动力测试结果及计算模拟进行了砖石古塔动力特性研究,并对古塔震害基本规律进行了分析。李胜才等[7]通过数值计算,模拟了龙护舍利塔的地震损伤演化过程,分析了该塔地震破坏机制。陈平等[8-9]结合小雁塔、崇文塔结构安全性评估工作,采用增量动力分析法对小雁塔进行了地震易损性分析,并采用数值方法对崇文塔进行了抗震能力计算,探讨了古塔结构抗震性能评估方法。张文芳等[10]建立了施加等效水平地震侧力时古塔结构的有限元模型,分析了太原晋祠舍利生生塔墙体弯曲破坏时受拉、受压区的失效过程,研究了太原晋祠舍利生生塔地震内力及承载力。

综合相关研究可以发现,砖石古塔结构损伤机制是研究结构抗震性能的基础之一。古塔结构损伤后,导致结构自振频率降低或阻尼比增大,因而结构动力特性能够反映结构的损伤状态。而古塔结构损伤之前的动力特性值可通过数值计算获得,并采用原位动力测试方法获得损伤古塔结构的动力特性,对测试参数及计算参数进行数据归一化处理后,得到结构的整体等效力学计算参数,可依据该参数进行地震作用下古塔结构损伤分析。为此,本文通过原位动力测试及数值计算,分析陕西省崇寿寺宋代砖塔结构在地震作用下损伤参数的变化,探讨其地震损伤机制,为砖石古塔结构抗震分析提供参考。

1 崇寿寺塔概况

崇寿寺塔亦称蒲城北塔(见图1),位于蒲城县城关镇西太街东段北侧,始建于北宋绍圣三年(公元1096年),为13级密檐式砖塔,残存高度为46.23 m,首层底面外边长8.28 m,塔室内边长3.1 m,墙厚约2.5 m。明嘉靖年间遭受地震,塔身受损,塔顶掉落,清乾隆三十五年(公元1770年)修补塔基,1985年陕西省政府对其进行大修,现为国家重点文物保护单位。

2 基本力学参数的确定

因文物保护的要求,不允许对古塔结构进行破坏性试验,结构材料的力学计算参数难以通过实测确定,故依据动力特性测试结果确定古塔的等效弹性模量。由结构动力学原理可知,地震作用下古塔结构的动力响应与动力特性密切相关,结构地震响应对结构损伤的产生及累积模式影响显著。同时采用有限元方法进行结构动力特性计算时,弹性模量的取值与动力特性的计算结果直接关联。因此,可通过修正弹性模量的取值,使古塔结构振动周期与测试结果保持一致,从而确定古塔的等效弹性模量。

图1 崇寿寺塔Fig.1 Chongshousi Pagoda

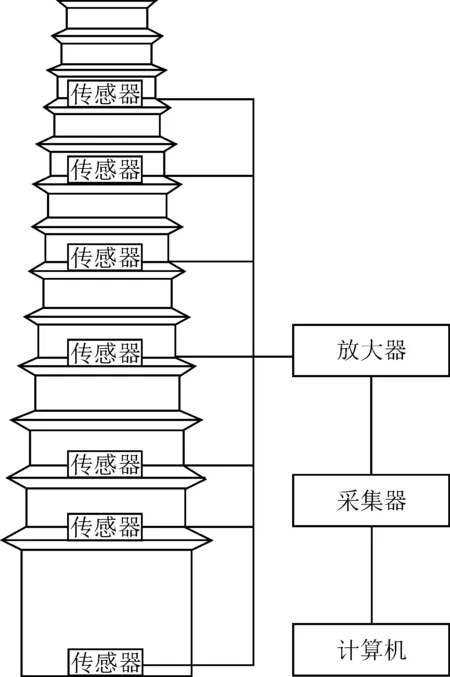
图2 动力测试方案Fig.2 Dynamical test program

2.1 动力特性测试

为测试崇寿寺塔的动力特性,在文物及古建筑管理部门协助下,临时限制对古塔参观,如图2所示。

各楼层测点布置7个941B型超低频拾振器,将拾振器与结构可靠粘结,并与信号放大器及采集器连接后,分别采集3次30 min在地脉动激励下古塔各楼层沿东西方向与南北方向持续振动的信号,见图3,其中测点1为地面脉动信号,其余测点为塔体结构的振动信号。

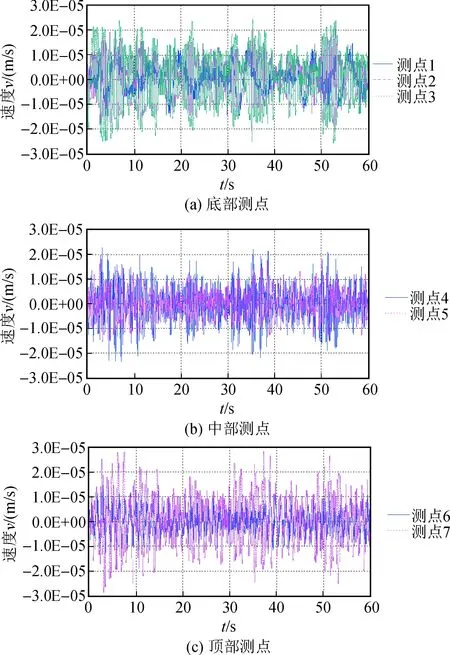
图3 楼层振动时域信号Fig.3 Vibration signal at each floor in time domain

由图3可见,塔体结构上各测点的振动信号具有一致性。对振动信号进行滤波及快速Fourier变换,完成频域分析,见图4,结构上各测点频域曲线中峰值点所对应的频率值即为古塔的各阶频率。将各测点对应的同阶频率值取平均值,得到该塔的前3阶振动频率见表1。

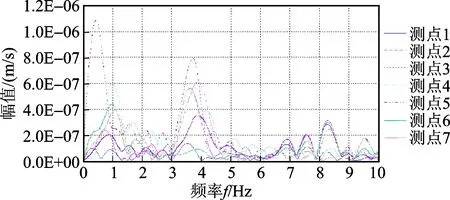
图4 各测点频域信号Fig.4 Vibration signal at each floor in frequency domain

表1 崇寿寺塔自振频率测试结果Tab.1 Test results of vibration frequencies of Chongshousi Pagoda

2.2 动力特性计算

基于通用有限元软件ABAQUS计算平台,依据崇寿寺塔结构尺寸建立数值模型,按空间四面体划分计算单元,见图5,通过模态分析计算各阶自振频率。

图5 有限元模型Fig.5 FEM model

因古塔损伤引起结构整体刚度减小,进而使结构自振频率降低。数值计算中,材料密度及弹性模量取值显著影响自振频率的计算结果,结构损伤对古塔密度影响较小。参考相关文献及现场调研结果,塔体材料密度ρ取1 800 kg/m3。将古塔结构等效为均质弹性体,通过选取不同弹性模量值进行试算,结果表明,当等效弹性模量取1 800 MPa时,计算所得该塔的前三阶频率与实测结果的最大误差为5%,吻合较好,故可将该塔的整体等效弹性模量确定为1 800 MPa。采用Rayleigh阻尼,阻尼系数参考相关文献取值为:α=0.223 5,β=0.001 86[10]。

3 砌体损伤模型

3.1 应力-应变关系

崇寿寺砖塔砌体以黄泥浆砌筑,目前尚无成熟的本构模型。通过对比现有砌体本构模型可以发现,各模型中的受压应力-应变曲线在上升段较为接近,而在下降段却区别较大,尤其在高应变区段则更为显著。因该塔结构砌体残损较为严重,故选择在高应变时与试验结果吻合较好的杨卫忠模型,其表达式如下[11]:

上升段:σ=Ecε(0≤ε≤εc)

(1)

下降段:

(2)

式中:σ与ε分别为砌体压应力及与其对应的压应变;Ec为初始弹性模量;η为初始切线模量与峰值割线模量的比值,取η=1.633;εc为应力应变达到顶点时的应变;fc为砌体轴心受压强度峰值。

古塔砌体抗拉强度较低,受拉后易发生砌筑缝开裂破坏,故采用考虑应变软化效应的双折线简化模型,应力-应变关系如下[12]:

σt=Ecε(ε≤εt)

(3)

(4)

式中:σt与ε分别为砌体拉应力及与其对应的拉应变;εt为弹性极限拉应变;ft为砌体轴心受拉强度平均值。

参考相关文献[11],计算时εc取0.002,fc取0.6 MPa,εt取0.001,ft取0.06 MPa。

3.2 损伤模型

在地震作用下,古塔砌体中的初始缺陷引起局部损伤,将结构分割成若干个独立的受力单元,各单元间的相互作用引起结构损伤逐步累积,导致部分单元失效,宏观上表现为应力-应变关系在峰值点后出现软化。依据能量等价原理[13],将损伤单元材料的弹性余能与无损结构材料的弹性余能以相同的形式表示,式(5)～(6)分别为无损结构材料与损伤材料的弹性余能表达式,并将应力改为等效应力。

(5)

(6)

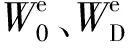
按弹性余能相等原则,因结构损伤后的表观应力为σ′=σ/(1-D),则由式(5)～(6)可得:

σ=E0(1-D)2ε

(7)

将式(7)引入砌体应力-应变关系,可得受拉及受压状态的损伤演化方程如下[14]:

(8)

(9)

式中:Dc为受压损伤因子;Dt为受拉损伤因子。

4 数值模拟

4.1 损伤参数

将计算软件中混凝土塑性损伤模型的计算参数按式(8)～(9)修正后进行输入,实现地震作用下拉伸断裂和受压破坏的模拟,在满足收敛条件下,当损伤参数D达到0.95时结构发生损伤破坏。

4.2 地震波输入

崇寿寺塔位于7度设防区,Ⅲ类场地,故选用EL-Centro波进行输入,截取包含强震时段共30秒的记录,峰值加速度对应的时间点位于[0,5]内,其波形见图6。在小震作用下古塔处于弹性阶段,结构未发生损伤。对中震及大震加速度峰值分别按100 gal、220 gal进行调幅。

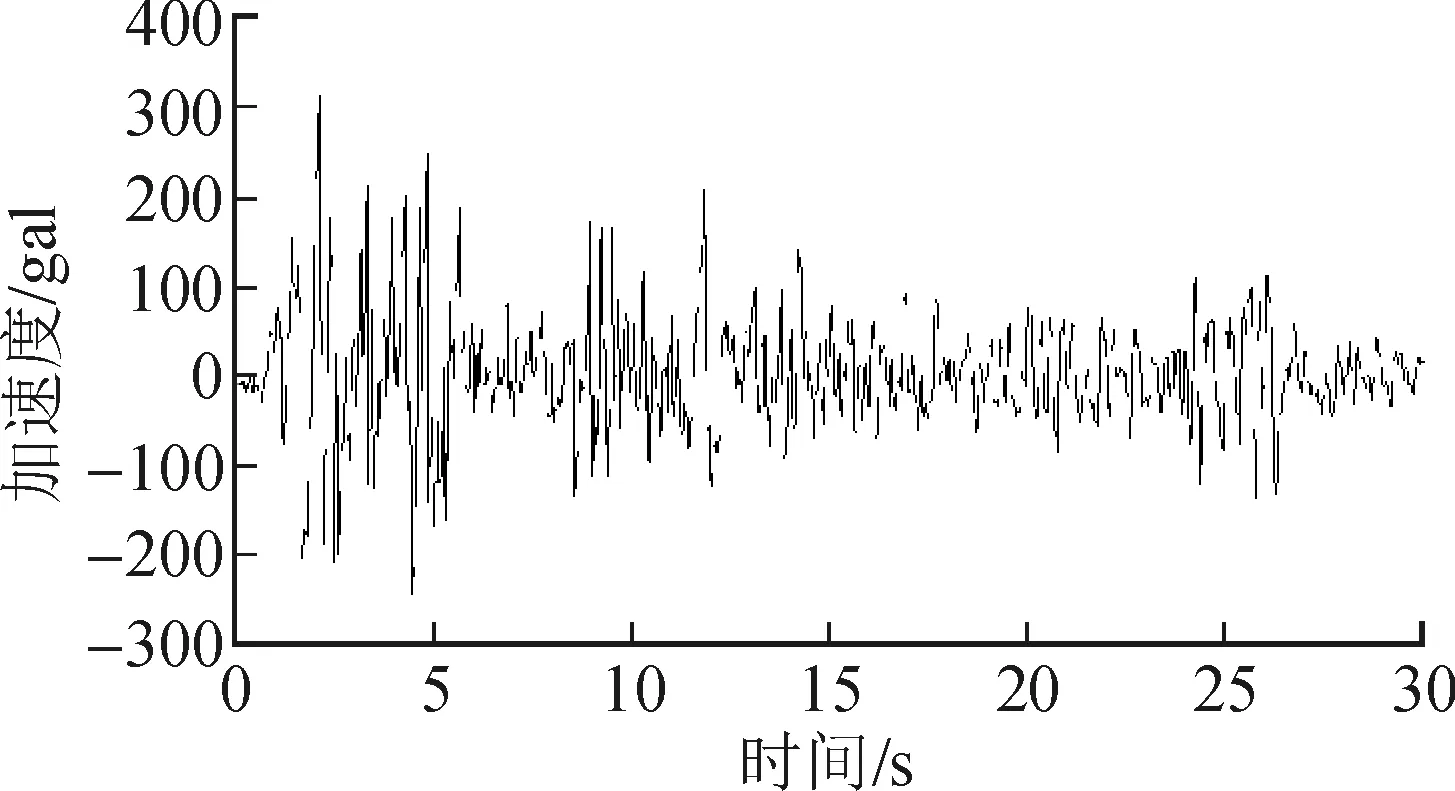
图6 EL-Centro波Fig.6 EL-Centro wave

4.3 地震损伤分析

输入EL-Centro波计算后,得到地震作用下古塔结构损伤的计算结果,见图7～8。

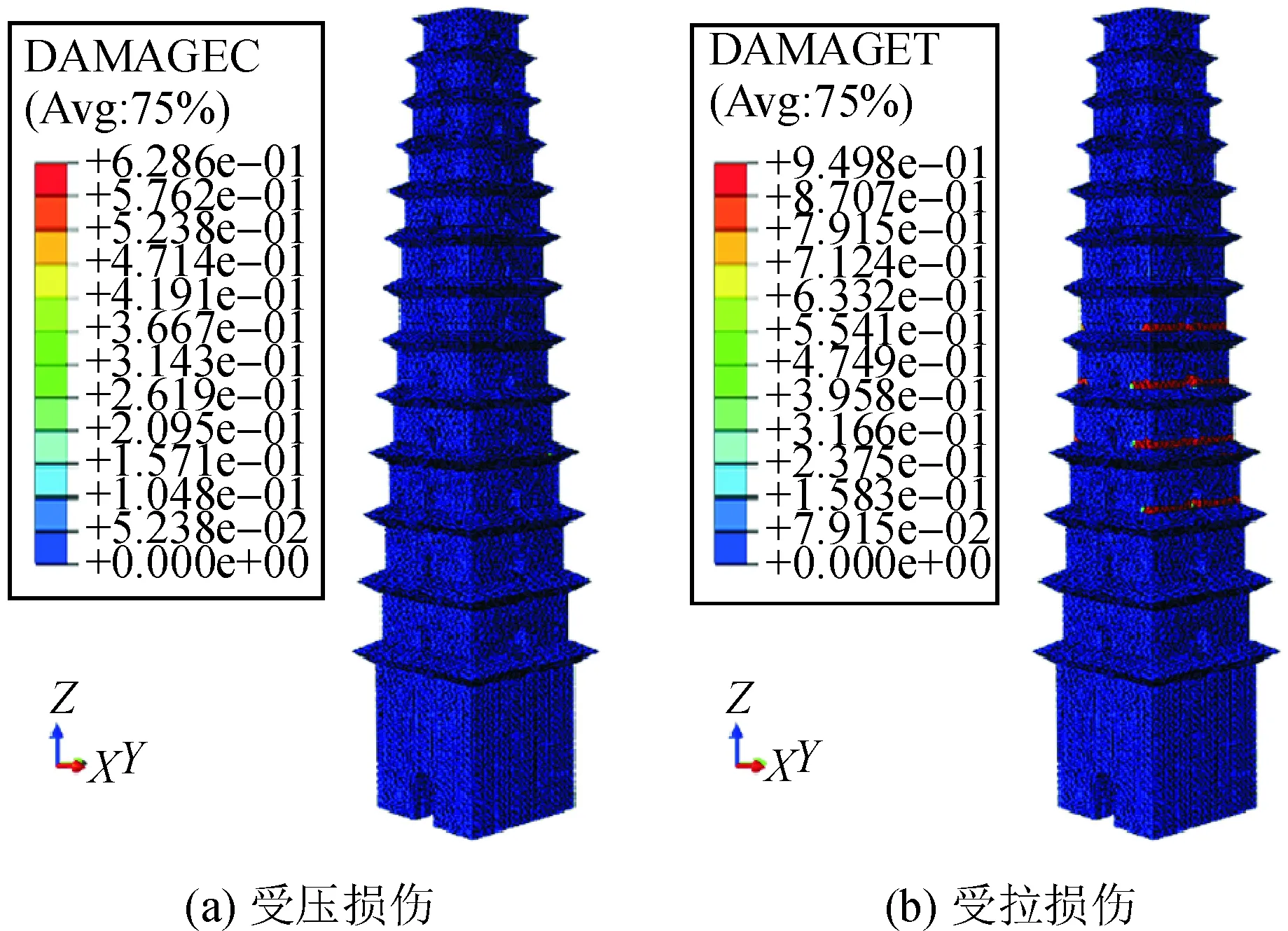
图7 中震作用下古塔损伤Fig.7 Damage situation of pagoda affected by medium earthquake

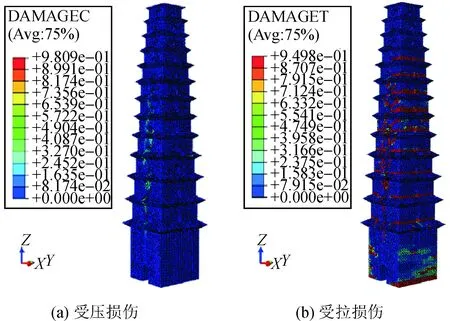
图8 大震时古塔损伤状态Fig.8 Damage situation of pagoda affected by strong earthquake

由图7可见,中震作用下古塔结构不会发生受压损伤;但因结构楼层随高度增加其截面变化较快,特别是中部楼层,地震作用下因结构整体弯曲变形在该部位产生了较大的拉应力,局部产生受拉破坏,导致受拉损伤最严重的区域为第4层至第6层底部。

在大震作用下,塔体结构开始发生受压损伤,见图8,结构发生较大的整体弯曲及剪切变形,结构中的主压应力达到砌体抗压强度,在第3层至第7层洞口周边出现显著的受压损伤区。且由图8(b)可见,除顶部3层外,其余楼层均发生受拉损伤,损伤严重的区域为各楼层底部及窗洞周边,首层约2/3层高范围内均产生一定的损伤,但其损伤程度不及其余楼层显著。

通过对比输入地震波后古塔各楼层地震损伤因子的变化曲线,进行结构地震损伤累积分析,图9～10为结构楼层地震损伤因子的变化曲线。

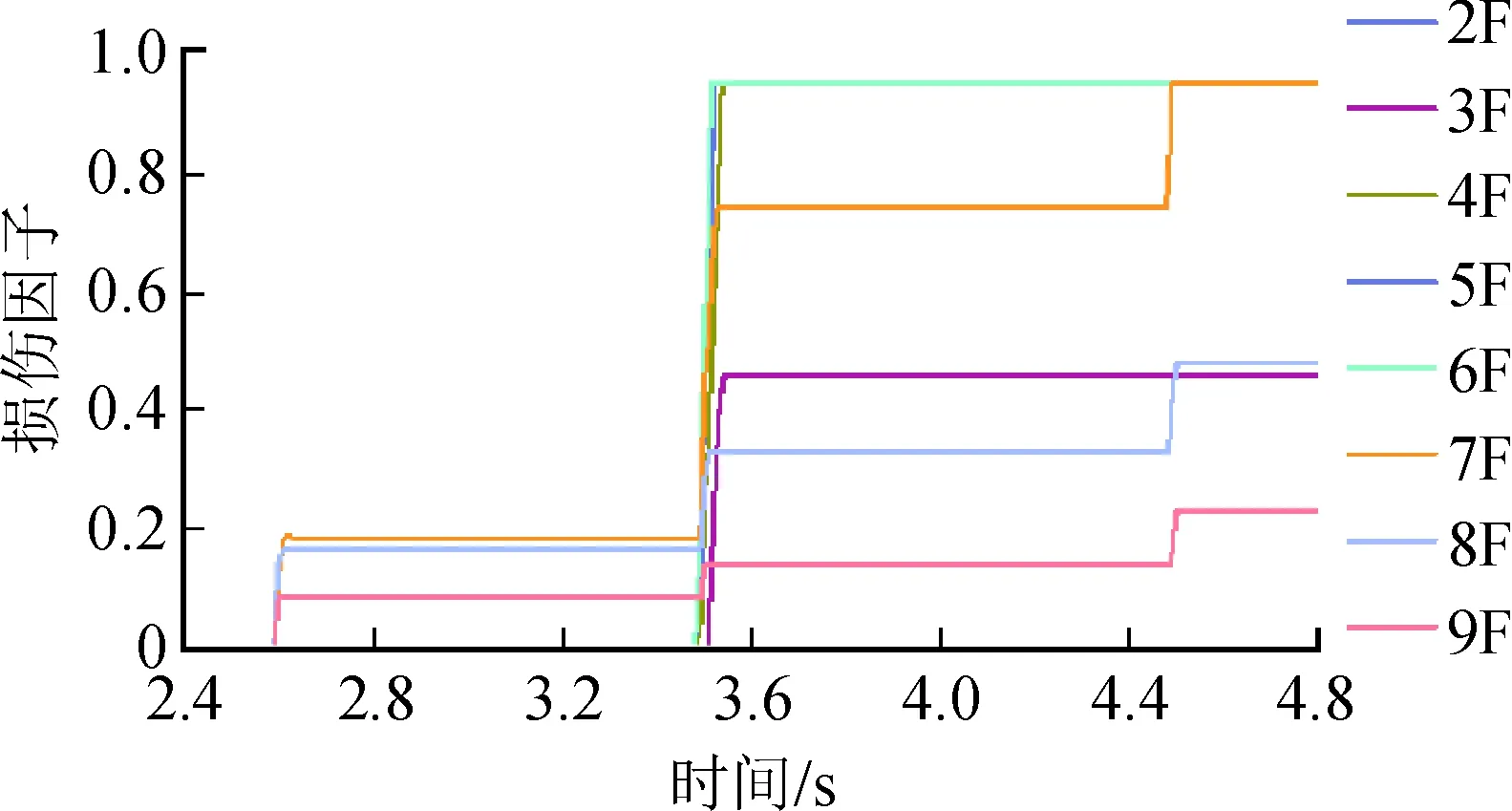
图9 中震作用下结构损伤因子变化Fig.9 Structure damage factors in medium earthquake

由图9可见,在中震作用下,当t=2.6 s时古塔结构开始出现受压损伤,损伤起始于顶部楼层,随着地震波持续作用,损伤因子增加不显著;当t=3.5 s时,7层以下结构损伤因子迅速增加,而后保持稳定,其中6层及7层损伤因子值最大,表明地震作用下该部位楼层损伤最为严重。

图10 大震作用下结构损伤因子变化Fig.10 Structure damage factors in large earthquake

在罕遇地震作用下,各楼层受压损伤因子迅速增大,由图10可见,t=2.4 s时结构各楼层均发生受压损伤,且迅速增长并保持稳定,除3层及5层外,其余各楼层损伤因子均超过0.8,表明结构受压损伤明显且范围显著增大。

由各楼层出现损伤的起始时刻(见图11)可以发现,当峰值加速度为100 gal时,塔体受拉损伤开始于第7、8、9三个楼层;而当峰值加速度为220 gal时,塔体受拉破坏则从第6层开始。

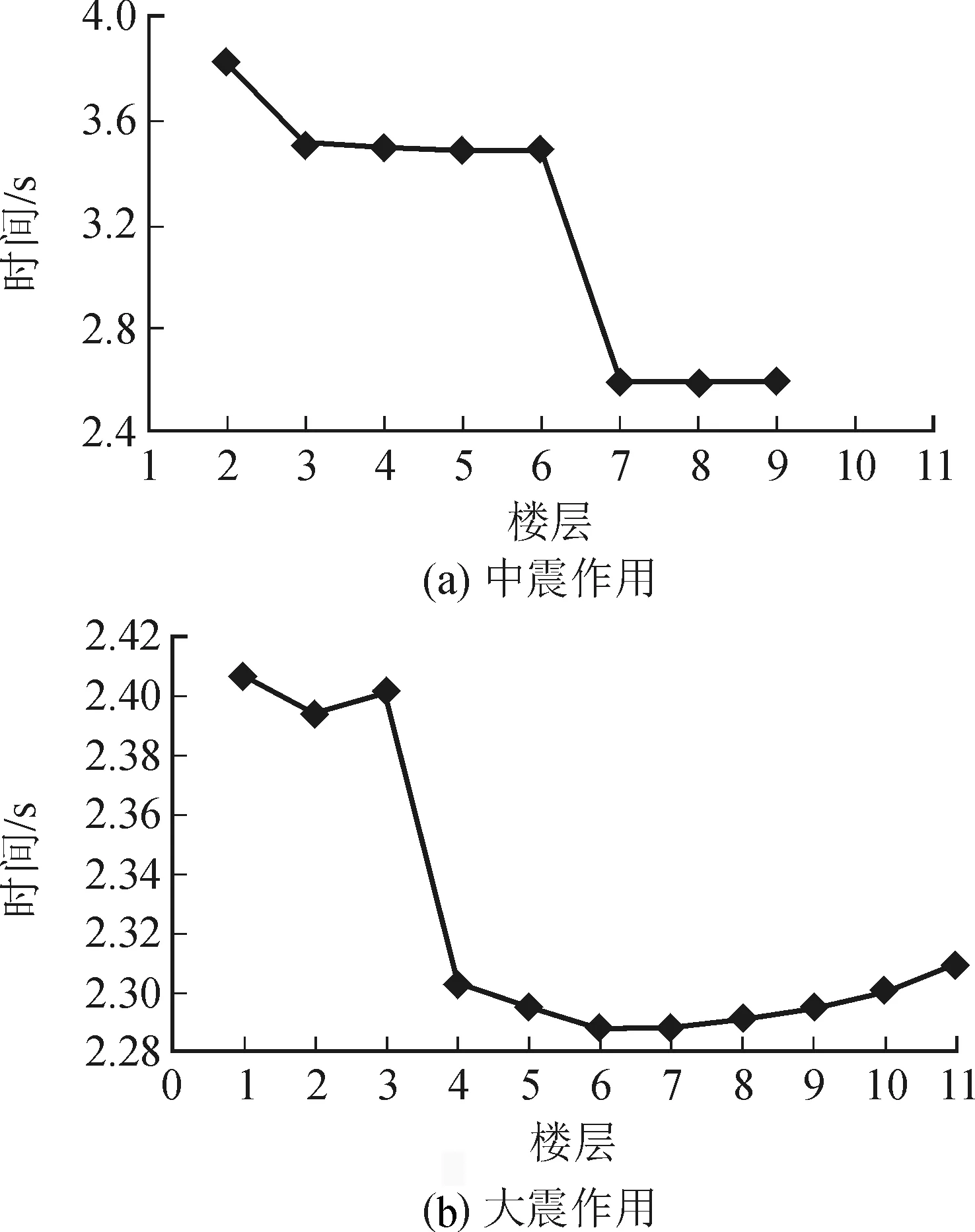
图11 结构楼层损伤起始时刻Fig.11 Initial time of structure damage in each floors

综合结构损伤分析结果可见,崇寿寺塔在中震作用下基本不发生受压损伤,仅在中部局部楼层发生受拉损伤,结构基本完好;在大震作用下,中部楼层洞口周围发生局部受压损伤,而受拉损伤破坏的区域较大,且受拉损伤开始于第6层,而后向其它楼层转移并逐步累积,底层为受拉损伤最严重部位。

5 结 论

依据崇寿寺塔原位动力特性试验结果,按结构动力特性一致的原则确定古塔的等效弹性模量,分别输入中震及大震条件下的地震波,计算了结构的地震响应,分析了古塔地震损伤的累积规律,主要结论如下。

1) 按古塔结构振动频率计算结果与测试结果相等的原则确定结构的整体等效弹性模量,可满足地震作用下结构动力响应一致的要求。

2) 中震作用下崇寿寺塔结构不发生受压损伤,受拉损伤最严重区域位于中部楼层;在大震作用下,古塔中下部楼层洞口周围产生显著受压损伤区,且结构楼层均发生显著的受拉损伤。

3) 在中震作用下,古塔结构受拉损伤开始于顶部楼层,在罕遇地震作用下,各楼层结构的损伤因子迅速增加,受拉损伤开始于第6层。

4) 地震作用下古塔结构破坏主要由受拉引起损伤累积,结构底部与中部楼层为损伤破坏显著区域。