自然环境条件下混凝土徐变预测模型

王永宝, 贾 毅， 廖 平， 赵人达

(1. 西南交通大学 土木工程学院， 四川 成都 610031； 2. 太原理工大学 建筑与土木工程学院， 山西 太原 030024)

处于自然环境条件下的混凝土徐变受多种复杂因素影响[1]，如混凝土强度、水泥类型、水灰比、养护条件、加载龄期等。上述因素中，混凝土强度、水泥类型等内部影响因素在桥梁施工完成后已确定，而日照、降雨、温度和相对湿度等外部因素仍处于不断变化中。已有研究表明，由温度引起的混凝土徐变可达20 ℃标准环境的2～4倍[2]，交变温度和相对湿度也显著影响混凝土徐变[2-7]。处于变化中的温度和相对湿度等因素会影响混凝土徐变，而桥梁结构长期变形的计算精度又受混凝土徐变预测模型影响较大[8]，为得到合理的桥梁长期变形行为，需进一步探讨自然环境条件下的混凝土徐变预测模型。

目前已有较多模型可用于计算非恒定温度下的徐变效应，如BP-KX[9]、B3[10]、B4[11]、罗俊礼模型[12]、CEB90[13]、CEB10[14]、张子明模型[15]、Rao模型[16]和汪剑模型[17]等。除上述模型外，Schwesinger[6]和Fahmi[7]等对变化温度下的轴压和受扭构件进行长期变形试验，基于试验结果，提出了混凝土徐变预测模型；Illston[18]等将变化温度下的徐变分为弹性应变、滞后弹性应变、瞬时温度应变和流动应变，得到了适用于大于20 ℃的交变温度的徐变预测模型，但采用隐式方程求解，计算复杂，不便于工程应用；Schneider[19]等对Bazant教授的双幂定律模型进行修正，认为高温状态下混凝土的瞬态温度应变与时间无关，并给出了瞬态徐变计算公式。

与温度相比，交变相对湿度也对混凝土徐变有一定影响。Bazant提出的基于微预应力固结理论的变化温、湿度下混凝土徐变预测模型需求解微分方程[20]；Vidal对文献[20]的微预应力固结理论模型进行了简化，但仍需求解微分方程，工程应用复杂；汪剑[17]综合CEB90模型和Fahmi[7]研究成果，探讨了变化温度、相对湿度及构件理论厚度下的徐变模型；Rao[16]等对CEB90模型进行了改进，得到了适合于大体积混凝土的徐变预测模型；杨永清等[21]基于试验结果，拟合了自然环境条件下混凝土徐变预测模型；Gasch[22]等对文献[20]的微预应力固结理论进行改进，得到了变化环境条件下的混凝土徐变预测模型。虽然目前已有较多模型可同时考虑温度和相对湿度对混凝土徐变的影响，但由于各模型对温、湿度考虑因素不同，使上述模型之间存在较大区别，其对自然环境条件下的混凝土徐变计算适用性仍需进一步探讨。

本文对既有变化温、湿度作用下的混凝土徐变预测模型进行了对比分析，探讨了各预测模型之间的差异性。在此基础上，收集了45组温、湿度作用下的混凝土徐变试验数据，提出了混凝土徐变预测模型公式，并进行了验证。

1 既有徐变预测模型对比

考虑温度效应的徐变预测模型有BP-KX[9]、B3[10]、CEB90[13]、CEB10[14]、B4[14]、罗俊礼模型[15]、Rao模型[16]和汪剑模型[17]等。其中，BP-KX[9]、B3[10]和B4模型[11]是通过等效时间法考虑了温度对徐变的影响；而罗俊礼[12]等认为温度、湿度和构件理论厚度之间相互独立，通过线性拟合法，得到了变化温度下的混凝土徐变计算公式。上述模型中，除Fahmi采用增量法外，其余模型均采用全量法计算徐变应变。

为探讨上述各模型的差异，本文以文献[5,7,23]的试验结果为例，分析在非标准恒定温度、非标准交变温度及交变温、湿度作用下计算结果的异同。相关混凝土材料特性见表1[5,7,23]。

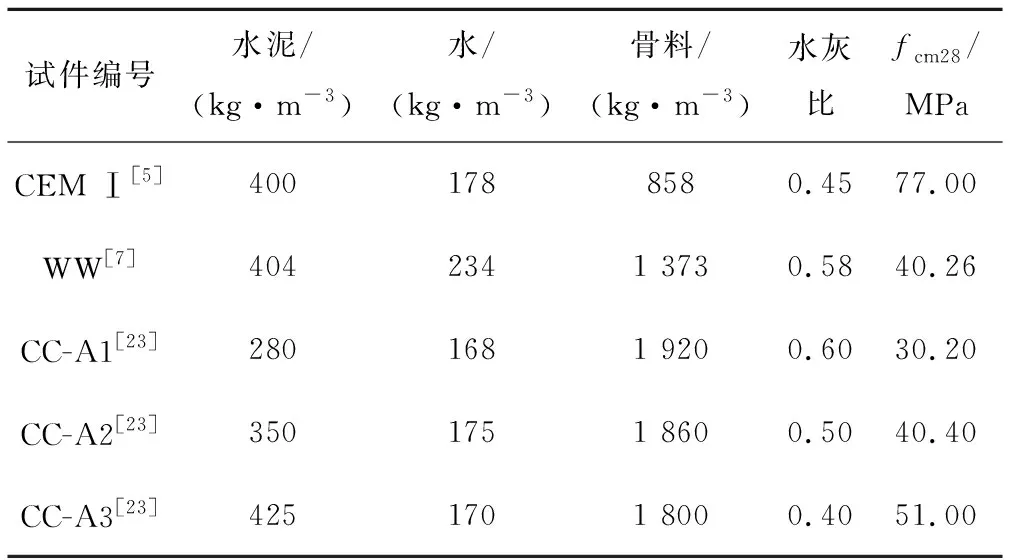
表1 混凝土材料特性

1.1 非标准恒定温度

表1中CEM Ⅰ为Φ×h=100 mm×220 mm的圆柱体试块，三组试分别在20 ℃水中养护300、427、300 d后，分别放置在20、50、80 ℃的密封环境中施加26.1、25.8、26.1 MPa的应力，进行280 d的徐变观测。

图1给出了在三种温度下，BP-KX、B3、B4、CEB90、CEB10、汪剑模型、Rao模型和罗俊礼模型的计算结果与试验结果的对比情况。由图1可知， BP-KX模型在20C时，低估实测值，在50 ℃和80 ℃时，高估实测值，该模型对温度敏感性明显大于其他两种模型；B3模型对温度的敏感程度介于BP-KX和B4模型之间，虽然结果比BP-KX模型小，但在温度为50 ℃和80C时，也显著高估徐变应变；B4模型对温度的敏感性较差，在温度较低时，高估徐变，在温度较高时，低估徐变。由于模型相似性，在20C时，汪剑、Rao和CEB90模型的计算结果相同；但汪剑和Rao模型对温度的修正方式不同，因此在50 ℃和80C时，Rao模型的结果低于汪剑模型。此两种模型均低于试验结果。CEB10模型在所有的模型中计算结果最小，由于罗俊礼模型包含瞬态温度徐变效应，其对温度的敏感性较大。

1.2 非标准交变温度

文献[7]试件尺寸及养护条件见表2，材料特性见表1的WW试块。试件成型后，在23 ℃环境中养护并加载持续时间为150 d的6.64 MPa应力。交变温度下BP-KX、B3、汪剑模型和Rao模型的计算结果与试验结果对比情况见图2。由于微预应力固结理论[20]及其改进方法较为复杂，本文未计算。

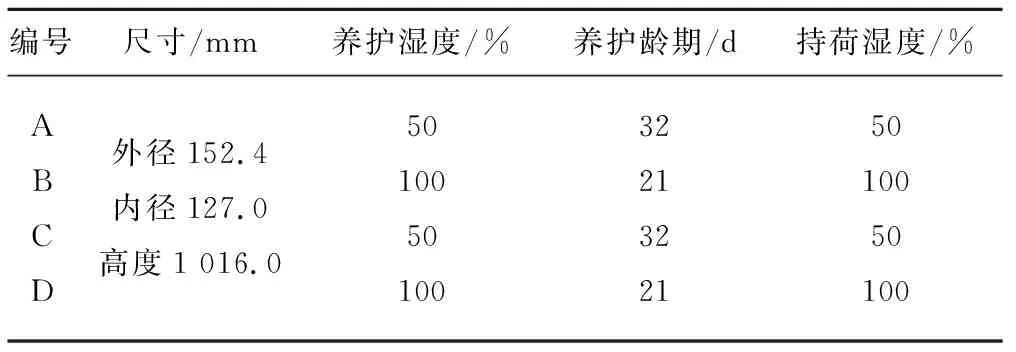
表2 文献[7]试验概况

由图2可知：当相对湿度RH=50%时(A和C)，首次升温时，徐变应变有较大增幅，后期变化较小；当RH=100%时(B和D)，除首次升温时增幅较大外，后续升温阶段徐变增量仍较大。但预测模型分析结果仅在第一次升温时有较大徐变增量。

BP-KX模型在RH=50%时(A和C)，高估试验结果；RH=100%时(B和D)，低估试验结果。B3模型是通过在基本徐变项后乘以系数的方法考虑温度对徐变的影响，未考虑温度对干燥徐变的影响。而汪剑和Rao模型对温度敏感性较小。上述分析表明，汪剑和Rao模型低估试验结果，BP-KX模型高估试验结果，各个模型之间有较大差异。

1.3 交变温度和相对湿度

同时考虑交变温、湿度下的徐变预测模型主要有微预应力固结理论模型[20]、Vidal模型[5]、汪剑模型[17]和Rao模型[16]。上述模型中汪剑模型和Rao模型是CEB90模型的改进模型，其计算精度受改进模型影响较大。由于微预应力固结理论模型[20]和Vidal模型需求解微分方程，计算复杂，本节仅探讨汪剑和Rao模型在交变温、湿度下的徐变计算。

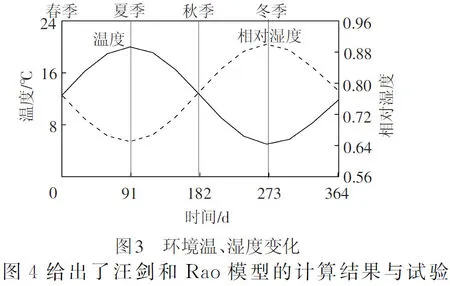
表1中CC系列的圆柱体试块(Φ×h=120 mm×300 mm)共12组[23]，成型后28 d放在图3所示环境中养护。每种混凝土四组，分别在春、夏、秋、冬四个季节施加15 MPa压应力。

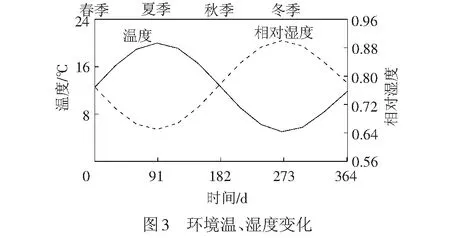
图4给出了汪剑和Rao模型的计算结果与试验值的对比情况。图4中结果为CC-A1，CC-A2和CC-A3三组混凝土徐变系数的平均值。由图4可知，当考虑变温、湿度时，Rao模型较汪剑模型大。春、季加载时，汪剑模型的计算结果与试验结果吻合较好；在秋、冬季加载下，上述模型均低估了试验结果。两种模型分析的秋季加载的徐变较小的原因是秋季加载后，温度下降，相对湿度增加，其徐变系数比春季和夏季小，但试验表明，秋季加载的徐变系数最大，分析原因可能是这两种模型仅从变化温度因素进行考虑，未将其分为变化和稳定部分。2.2节分析表明该差异主要体现在环境因素引起的稳定部分差异，而变化部分随时间变化曲线吻合较好。而春季加载的混凝土试件，浇筑后温度增加，相对湿度降低，徐变系数增加较快。由文献[16]的推导过程可知，Rao模型更适于大体积混凝土，汪剑模型[17]对非标准恒定温度下的徐变温度敏感性较小。

2 温度对徐变效应的影响

2.1 恒定温度影响

表3给出了收集的21组非标准恒定温度下徐变试验概况、ηave及δ取值。表3中，除Schwesinger的1、3组为干燥徐变外，其余均为基本徐变。表中ηave指自然或非标准环境下徐变系数与试验室标准环境下徐变系数的比值平均值，计算为

( 1 )

η(t)=φn(t)/φref(t)

( 2 )

式中：φn(t)和φref(t)分别为自然或非标准环境和试验室标准条件下的徐变系数。

由表3可知，所有试件持荷温度均大于20 ℃，加载龄期一般为10～14个月左右，即不考虑混凝土水化效应。虽然各个学者在不同条件下对不同强度等级的混凝土进行了徐变试验，但各试验结果之间表现出相似的规律：ηave均大于1；随加载龄期增大，ηave增加；混凝土强度越大，ηave越小。

图5给出了不同温度下η(t)随时间的变化情况[3]。由图5可知，6组试块的η(t)均大于1.0，且温度越高，η(t)越大，表明温度升高能增加徐变；当T=43 ℃时，η(t)随时间的变化较小；当T=71 ℃时，η(t)随时间的增加，在开始阶段增加较快，后期增加较慢，徐变系数随时间的发展呈现出明显的非线性变化，随着时间的增加，此效应增加较快。通过对比不同加载龄期的η(t)发现，龄期越大，η(t)越大。

Szucs[4]和Vidal[5]的结果见图6。由图6可知，Szucs和Vidal的η(t)较文献[3](见图5)大。当温度为40 ℃时，η(t)稳定在1.8左右；当温度为60 ℃和80 ℃时，η(t)在开始阶段较为稳定，30～60 d之间随时间增加逐渐增加，60 d后趋于稳定。图6(b)、图6(c)表明，水泥类型对η(t)也有影响，混凝土强度越大，η(t)越大；当温度为80 ℃时，两种类型的混凝土η(t)可达6～10。上述曲线中，仅温度为50 ℃的Ⅰ型混凝土(fcm28=77.0 MPa)的η(t)变化稳定在2.0左右；Ⅴ型混凝土(fcm28=65.0 MPa)在50 ℃时在200 d前增加较快，之后趋于稳定。

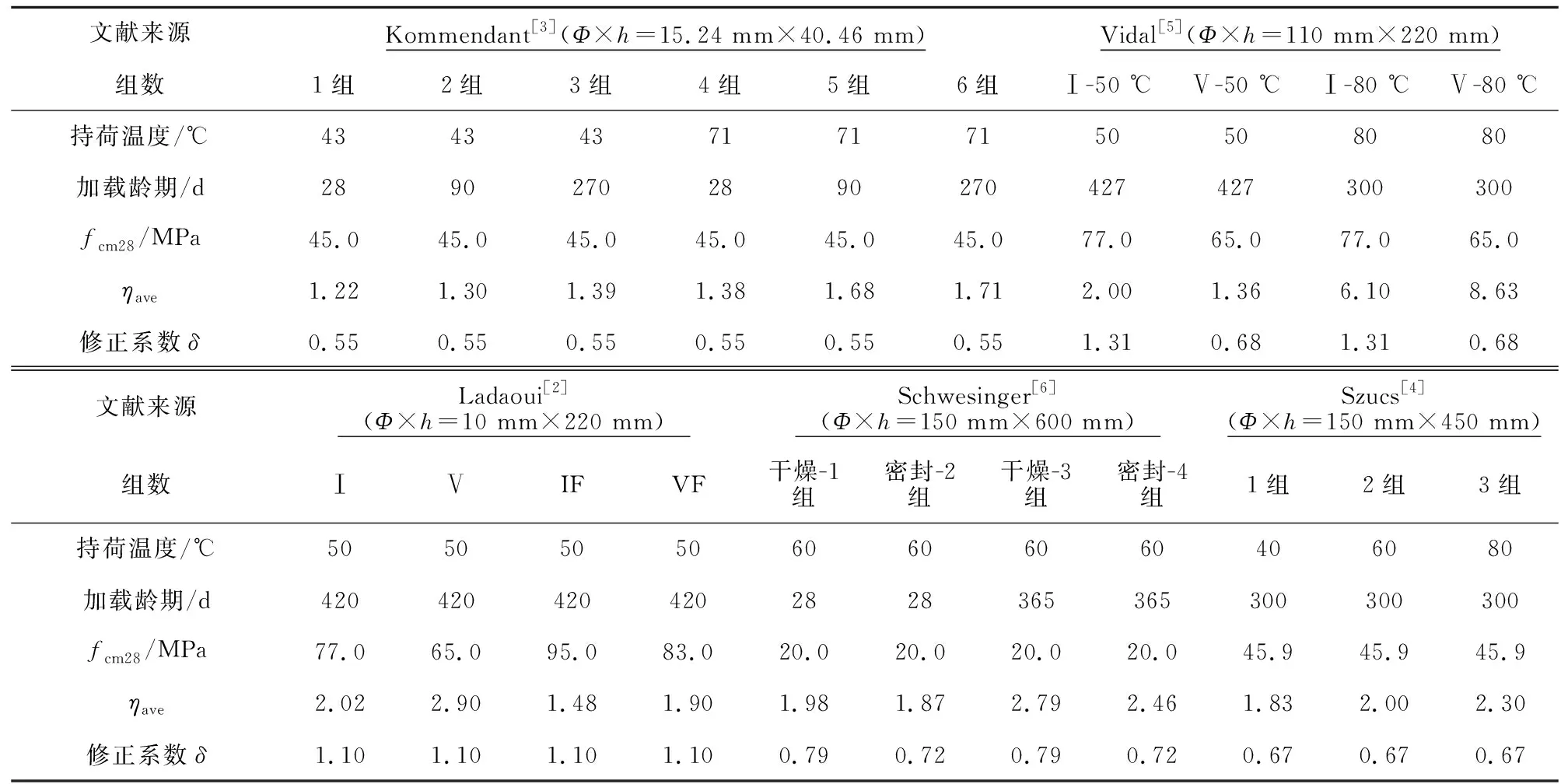
表3 徐变试验概况和相关参数

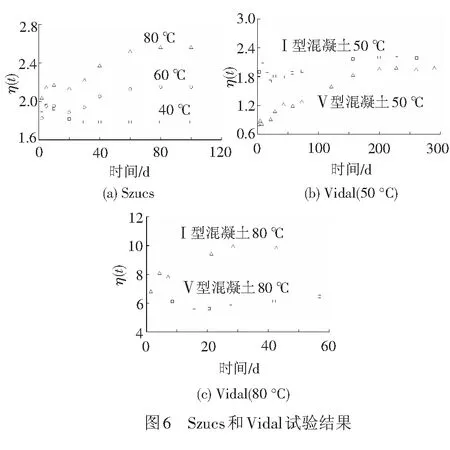
图7中，Ladaoui[2]的η(t)随时间的变化结果显示，除IF混凝土以外，其余三种混凝土的η(t)随时间变化较小；受到混凝土强度影响，不同类型混凝土ηave不同，混凝土强度越高，ηave越小，混凝土强度对徐变的影响与20 ℃下的徐变类似；且掺加粉煤灰的混凝土ηave比普通混凝土的徐变应变小。

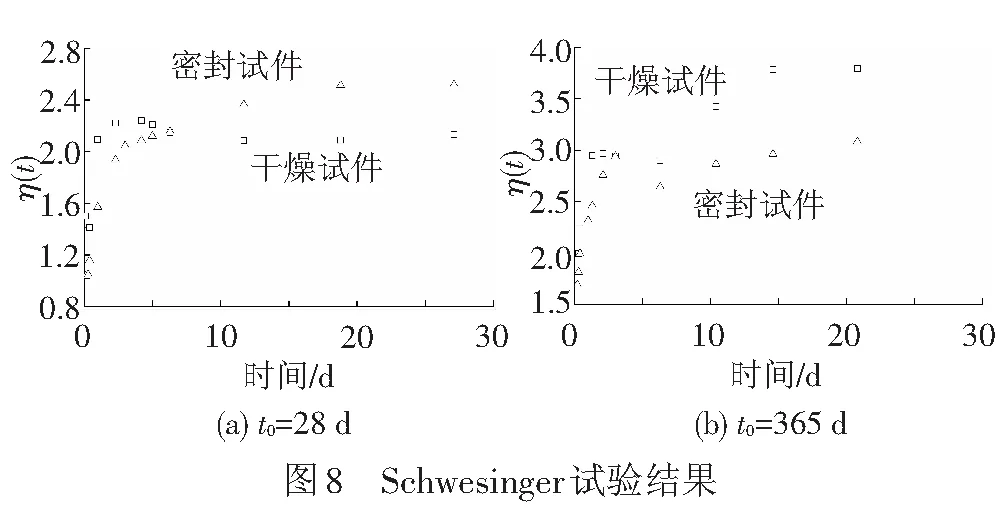
图8给出了Schwesinger[6]的短期徐变η(t)随时间变化情况。由图8可知，当T=60 ℃时，η(t)约为2.0～3.0，进一步证明了温度升高能增加混凝土徐变；t0=365 d的η(t)明显大于t0=28 d的试块，结论与文献[3]相同。η(t) 随时间变化稳中有进。

2.2 变化温度影响

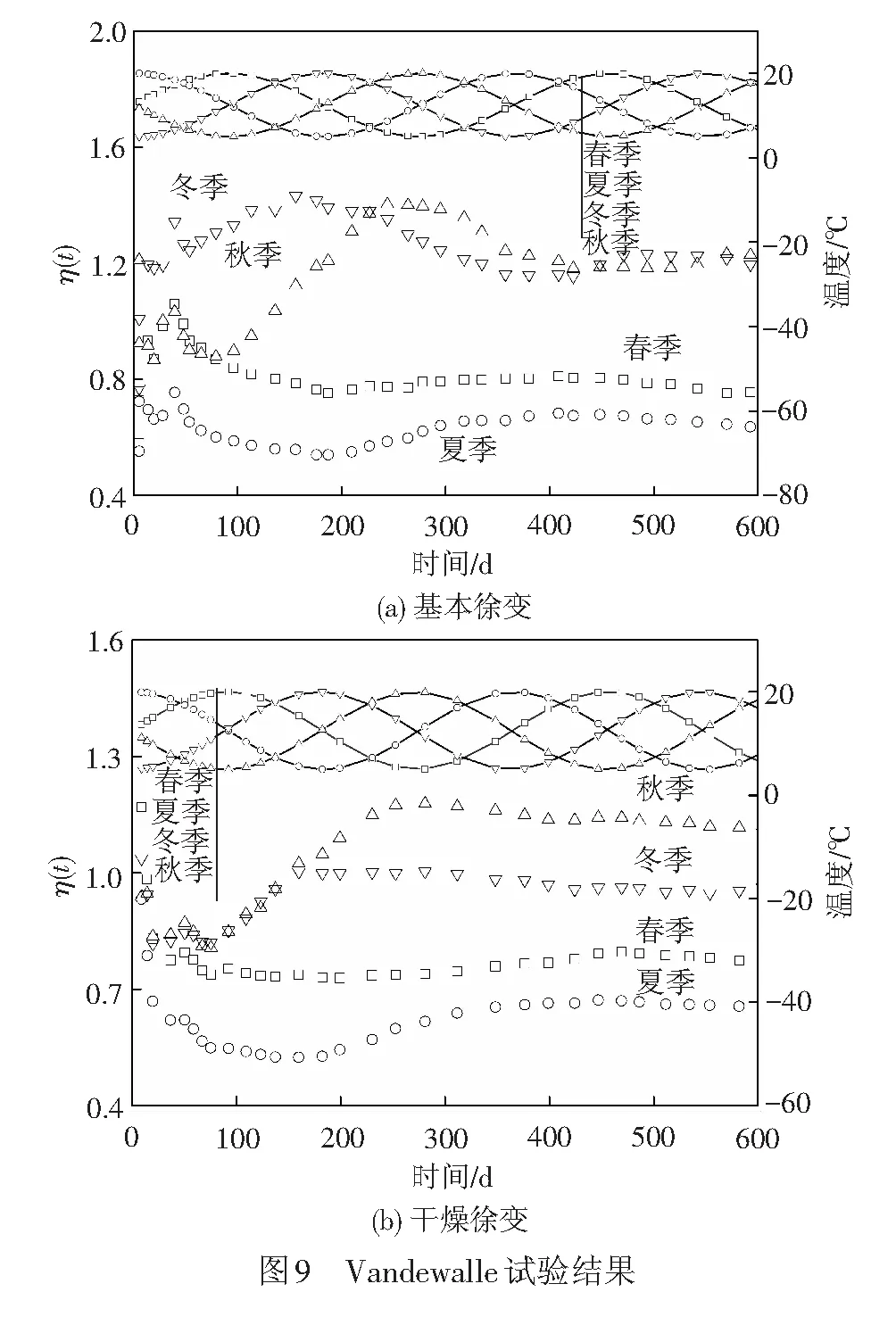
Vandewalle[23]以标准状态(T=20 ℃，RH=60%)下的圆柱体试块(Φ×h=120 mm×300mm，fcm28=40.4 MPa)为对比试块，进行了温度变化为5～20 ℃，相对湿度变化为65%～90%的自然环境条件下的徐变试验。Sakata[24]的徐变(l×w×h=100 mm×300 mm×400 mm，fcm28=36.9 MPa)试验，开始干燥和加载龄期均为14 d，不考虑风和降雨的影响，T=5～35℃，RH=55～65%，春夏秋冬开始的温度为14、29、25、8 ℃。由于原文未进行标准徐变试验，本文采用CEB10模型[14]计算。

表4给出了收集的16组不同季节的ηave和δ取值情况。由表4可知，不同季节浇筑的混凝土的ηave取值差别较大，对于Vandewalle[23]试验结果而言，由于试验环境的平均温度小于20 ℃，导致春、夏季的ηave出现小于1.0的情况。

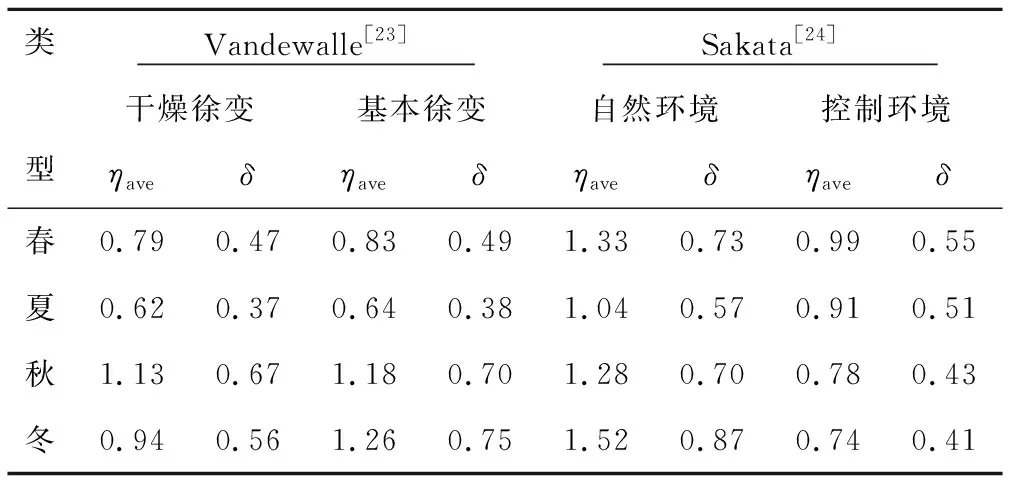
表4 Vandewalle和Sakata试验参数取值

图9给出了Vandewalle[23]的η(t)和温度随时间变化情况。由图9可知，温度对加载初期的η(t)影响较大；在加载后一年内，η(t)随时间的变化值与温度变化曲线趋势一致，证明温度是引起η(t)产生波动的主要原因；但第二年后，温度影响逐渐较小；无论是基本徐变还是干燥徐变，均是春季和夏季开始加载的η(t)小于秋冬季节；基本徐变的η(t)大于干燥徐变，主要原因可能是干燥徐变结果较大，分母较大，因此数值较小。由于η(t)随相对湿度的变化规律不明显，为节省篇幅，本文未在图9中给出相对湿度随时间变化曲线。

由图10(a)可知，不同季节浇筑的混凝土η(t)有较大差异。夏季η(t)最小，春季次之，冬季最大，规律与图9类似。且春季和夏季较为稳定，秋季和冬季在后期有较大的波动。由于原文未给出温度变化曲线，图10也未给出温度曲线。但为方便计算，基于文献[24]描述，自然环境下的温度变化方程为

T(t)=-15cos[2π/365·(t-t0)]+20

( 3 )

式中：t为计算开始时间，t≥5 d，春夏秋冬的t0分别为63、124、249、322 d。

图10(b)给出的人工控制环境的结果与自然环境结果类似，即当温度升高时，η(t)增大。但也有较大不同，如自然环境下的徐变为冬季加载最大，夏季加载最小，而人工控制环境则为春季最大，秋季最小。且人工控制环境下的η(t)明显小于自然环境，分析原因可能是试验室环境下的温度小于自然环境下平均温度导致的，且采用的人工控制环境与自然环境条件由一定差异。

3 相对湿度对徐变效应的影响

Cagnon[25]进行了两种加载龄期的圆柱体试块(Φ×h=118 mm×225 mm)在相同养护温度(密封和干燥)和变化相对湿度下的徐变试验。试块浇筑后放置在水中养护90 d，施加0.3fcm荷载，试验的混凝土水灰比，强度和弹性模量分别为w/c=0.43，fcm28=73.4 MPa，E28=42.8 GPa。Sakata[24]进行了8组变化相对湿度下的混凝土徐变试验，η(t)随时间变化见图11。

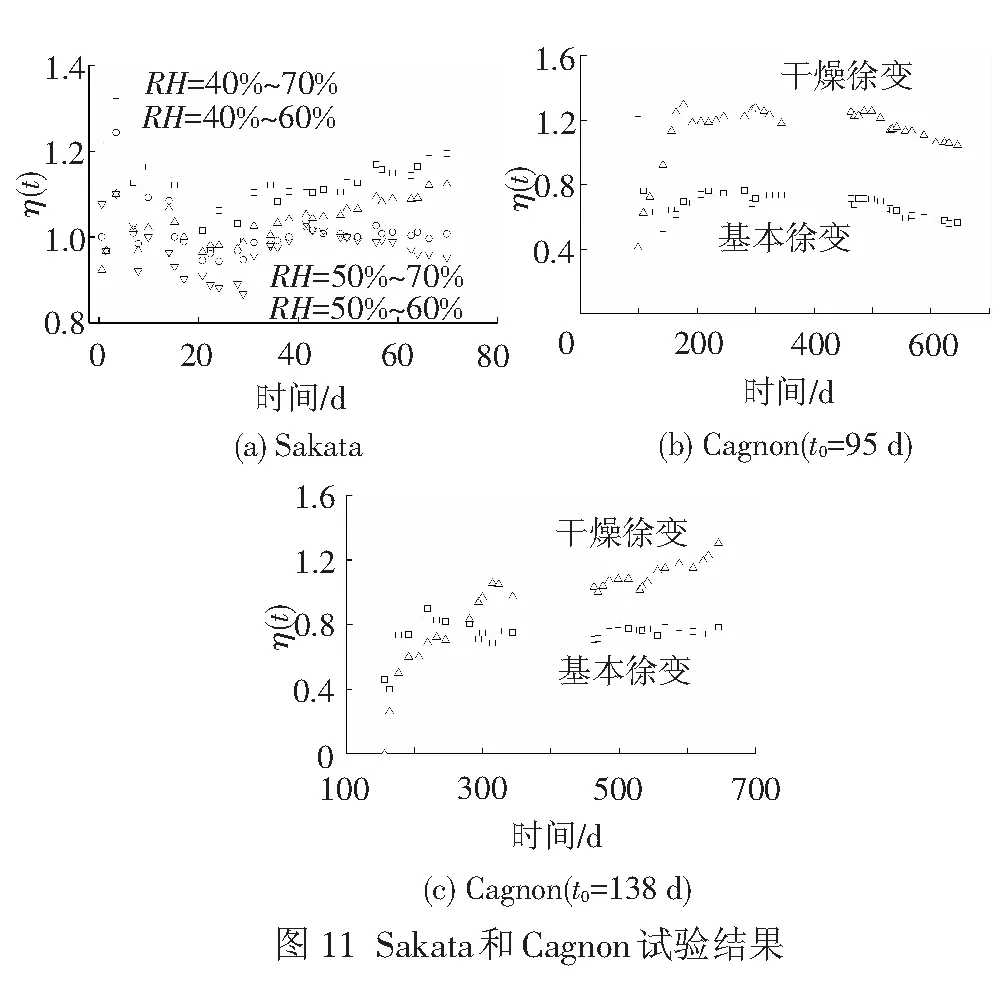
由图11可知，当温度恒定时，混凝土徐变受相对湿度的周期性变化影响，RH波动越大，徐变应变越大；最小RH越小，徐变应变越大。Neville[1]也指出周期性变化相对湿度的混凝土徐变比相应的相对湿度平均值下的徐变应变大，变化周期越短，徐变应变变化越大；首次干燥阶段对徐变效应影响较大，后期影响较小。交变相对湿度能影响混凝土的徐变效应，但对实际桥梁而言，箱梁尺寸较试件尺寸大[25-26]，其内部水分扩散较慢，仅表面相对湿度有一定变化，可认为周期变化短的相对湿度对混凝土徐变的影响较小。图11(b)、11(c)结果表明，不同加载龄期下，密封试件与非密封试件的η随时间变化不大，证明变化相对湿度对徐变的波动性影响较小，仅t0=138 d的干燥试件的系数随时间的变化增长较快；t0=95 d试件较为稳定。交变相对湿度对混凝土徐变的影响可通过平均相对湿度的方式加以考虑。

4 徐变预测模型分析

4.1 基本假定

(1) 混凝土徐变分为稳定和变化两部分，稳定部分与平均温度、加载龄期、平均相对湿度、强度、试验养护条件有关，变化部分与温度变化历程有关。

(2) 升温能增加混凝土徐变率，降温能减低徐变率，但徐变应变不随温度减小而减小。

(3) 混凝土强度增加能减小η(t)；加载龄期越大，η(t)越大；交变相对湿度与交变温度相比，对混凝土的徐变影响较小，可以通过修正系数方法考虑。

(4) 假定影响混凝土徐变的稳定部分各系数相互独立，可用连乘的方法确定。

4.2 徐变预测模型

自然环境条件下混凝土徐变预测模型为

φn(t)/φref(t)=βt′·βT·βfcm·δ+

( 4 )

βt′=1+ln(1+t′/1000)

( 5 )

( 6 )

( 7 )

式中：φref(t)为试验室标准环境条件下的徐变系数，若无实测数据时，可按CEB10模型计算，温度和相对湿度均取平均温度和相对湿度；βt′为加载龄期影响系数；βT为环境平均温度影响系数；βfcm为混凝土强度影响系数；t′为加载龄期；fcm28为28 d棱柱体轴心抗压强度，MPa；T为周围环境平均温度，℃；T(t)为t时刻，混凝土试块周围大气温度，℃；γ为养护条件影响系数，可取750；δ为其他因素修正系数。

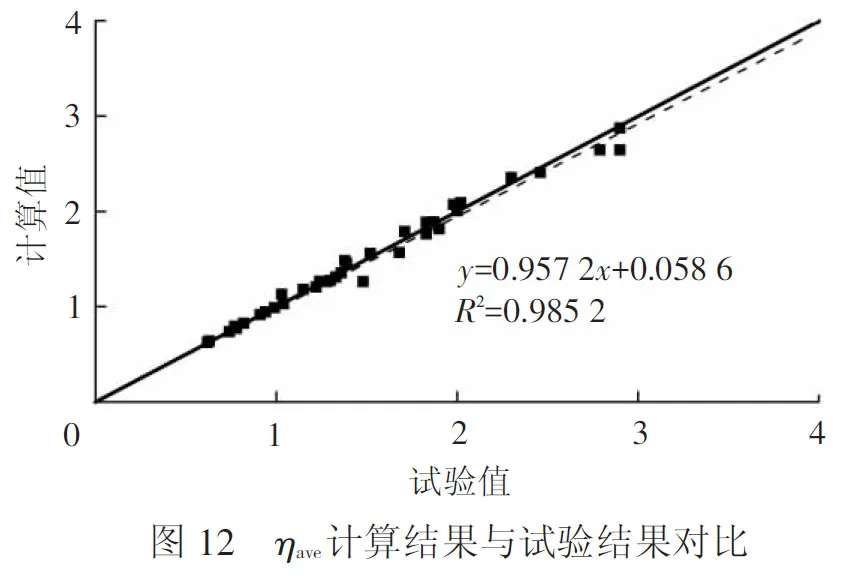
式( 4 )适用于恒定温度、交变温度和相对湿度下的徐变分析。若为恒定温度，式( 4 )右侧第二项为零，温度适用范围为20 ℃

本文模型不适于温度突变情况，因为处于自然环境条件下的外界环境温度是逐渐变化的，且对混凝土内部而言，温度的热传导作用也有一定的滞后性，使得温度变化是一个缓慢过程。

5 试验验证

为验证式( 4 )的正确性，图12列出非标准恒定温度和非标准交变温度下的ηave预测结果与试验结果对比。由图12可知，无论为非标准恒定温度还是交变温度下的稳定部分计算结果均与实测结果吻合较好，证明了式( 4 )右侧第一部分的正确性。

图13给出了非标准恒定温度(图13(a))和非标准交变温度(图13(b)、图13(c))的计算结果和实测结果的η(t)对比。受篇幅限制，本文只列举了部分结果对比。对非标准交变温度下的试验结果，虽然Vandewalle的部分试验结果与Sakata和常规分析结果存在差异，但由于目前国内外对交变温度和相对湿度下的徐变试验较少。且试验结果差异主要体现在式(4)的稳定部分，而变化部分与实测结果吻合较好[16]，因此本文用Vandewalle结果进行验证，虽然具有局限性，但能整体反映变化温度的影响。

由图13可知，处于不同季节浇筑的混凝土由于受到不同的温度和相对湿度变化历程，其徐变应变均不相同，式( 4 )能较为精确的计算自然环境条件下的混凝土徐变应变，具有较高精度，证明了式(4)右侧第二部分的正确性。

6 结论

(1) BP-KX、B3模型和罗俊礼模型对温度的敏感性较大，温度较高时高估徐变应变，可较为安全的评估温度作用下的徐变，但B3模型不再适用于降低温度情况下的徐变计算；汪剑模型、Rao模型、CEB90和CEB10模型对温度的敏感性较小，低估了交变温度下的徐变效应。

(2) 温度升高能增加混凝土徐变；在混凝土徐变计算时，应考虑温度引起的徐变效应；ηave随加载龄期增大而增加，随混凝土强度增加而减小；当温度低于50 ℃，温度影响下的混凝土徐变处于平稳状态；温度高于50 ℃时，呈非线性变化趋势。

(3) 受环境历程中的温度变化影响，不同季节浇筑的混凝土徐变应变不同；与温度相比，交变相对湿度对η(t)影响较小，在实际计算时，可采用综合效应系数δ统筹考虑。

(4) 自然环境条件与试验室标准环境条件下的徐变系数比可分为稳定和变化部分，稳定部分受平均温度、加载龄期、混凝土强度、试验养护条件影响，变化部分受温度时间历程影响；本文公式可用于预测自然环境条件下混凝土变形。

目前非标准恒定温度下的混凝土徐变试验对加载龄期较小或干燥徐变的试验研究涉及较少；对自然环境(降雨和太阳辐射作用)和试验室标准环境下的徐变试验对比研究，及变化相对湿度条件下的混凝土徐变试验研究较少。既有试验均未给出影响混凝土徐变的相关参数取值，导致本文公式具有一定局限性，公式正确性需要进一步验证。