平抛运动问题的归类与解题

广东 钟伟华 古焕标

平抛运动是曲线运动中的一类常见问题，是运动合成与分解的典型应用，也是高考考查的重点和命题热点。从近几年的高考命题形式来看，主要考查的是平抛运动的规律及速度(或位移)矢量三角形等相关知识，独立命题时常以选择题的形式出现，与能量、位移等相结合命题时常以计算题形式出现，预计今后高考将以生活实例为背景，综合力学中的其他知识考查对平抛运动规律的理解与应用。本文从平抛运动的解题思路和方法入手，探讨命题意图，总结解题技巧，供教学中参考。

一、基本规律

以抛出点为坐标原点，水平初速度v0方向为x轴正方向，竖直向下的方向为y轴正方向，建立如图1所示的坐标系，则平抛运动规律如下：

图1

位移关系：

速度关系：

二、问题归类与解题方法

对于平抛运动模型，可通过对做平抛运动物体的落点平面来进行分类，可分为落点在水平面上、竖直面上、斜面上、曲面上的平抛运动。解决平抛运动问题的方法需要看物体的落点的具体情况，假如物体的落点在水平面或竖直面上，直接应用平抛运动的基本规律解题；假如物体的落点在斜面或曲面(圆弧)上，首先要弄清斜面的倾角是位移的方向角还是速度的方向角，运用位移或速度的三角函数关系及平抛运动的基本规律进行解题。

1.落点在水平面上

1.1 模型结构

做平抛运动的物体落在水平面上，如图2所示。

图2

1.2 解题思路与方法

做平抛运动物体的落点在水平面上时，可采用运动分解的方法，把平抛运动看成是水平方向的匀速直线运动和竖直方向的自由落体运动的合运动。求解平抛运动的水平初速度时，首先想到的方法应该是从竖直方向上的自由落体运动求出时间，然后根据水平方向做匀速直线运动求出初速度。

【例1】(2015·全国卷Ⅰ第18题)一带有乒乓球发射机的乒乓球台如图3所示。水平台面的长和宽分别为L1和L2，中间球网高度为h。发射机安装于台面左侧边缘的中点，能以不同速率向右侧不同方向水平发射乒乓球，发射点距台面高度为3h。不计空气的作用，重力加速度大小为g。若乒乓球的发射速率v在某范围内，通过选择合适的方向，就能使乒乓球落到球网右侧台面上，则v的最大取值范围是

( )

图3

【解析】发射机无论向哪个方向水平发射，乒乓球都是做落点在水平面上的平抛运动。当发射机正对右侧台面发射，乒乓球恰好过网时，发射速度最小，由平抛运动规律：

当发射机正对右侧台面的某个角发射，乒乓球恰好到达该角时，发射速度最大，由平抛运动规律：

即速度v的最大取值范围为:

【答案】D

【感悟】平抛运动一定要和实际情况相结合，题目中，最小的水平位移一定要保证越过球网。解决本题的关键是要掌握平抛运动在水平方向和竖直方向上的运动规律，知道平抛运动的时间由高度决定，而水平位移由初速度和时间共同决定。

2.落点在竖直面上

2.1 模型结构

做平抛运动的物体落在竖直面上，如图4所示。

图4

2.2 解题思路与方法

当平抛物体落在竖直面上时，把平抛运动分解到水平方向和竖直方向去研究，水平方向做匀速直线运动，竖直方向做自由落体运动，两个方向上运动的时间相同。物体在空中运动的时间由高度h决定，与初速度v0无关，而物体的水平射程由高度h及初速度v0两者共同决定。由于竖直分运动为自由落体运动，则匀变速直线运动的解题方法和技巧都可以使用。

【例2】飞镖运动于十五世纪兴起于英格兰，二十世纪初，成为人们日常休闲的必备活动。一般打飞镖的靶上共标有10环，第10环的半径最小。现有一靶的第10环的半径为1 cm，第9环的半径为2 cm……以此类推，若靶的半径为10 cm，在进行飞镖训练时，当人离靶的距离为5 m，将飞镖对准第10环中心以水平速度v投出，g=10 m/s2。则下列说法中正确的是

( )

A．当v≥50 m/s时，飞镖将射中第8环线以内

B．当v=50 m/s时，飞镖将射中第6环线

【解析】此题属于小球做平抛运动落点在竖直面上的类型题，由题意知，第8环半径为3 cm、第6环半径为5 cm、第10环半径为1 cm、靶的半径为10 cm。当v=50 m/s时，根据平抛运动规律：x=vt

可知飞镖正好射中第6环线，当v≥50 m/s时飞镖将射在第6环线内；

若飞镖击中第10环线内，h≤1 cm=0.01 m，飞镖的速度至少为：

若要使飞镖击中靶子，h≤10 cm=0.1 m，飞镖的速度至少为：

【答案】BD

【感悟】本题考查平抛运动的规律，意在考查考生应用运动的合成与分解解决平抛运动问题的能力。

3.落点在斜面上

3.1 模型结构

平抛运动与斜面相结合的模型，其特点是做平抛运动的物体落在斜面上，包括两种情况：(1)物体从空中抛出落在斜面上，如图5甲所示；(2)从斜面上抛出的物体落在斜面上，如图5乙所示。

图5

3.2 解题思路与方法

【例3】(2013·上海卷第19题)如图6所示，轰炸机沿水平方向匀速飞行，到达山坡底端正上方时释放一颗炸弹，并垂直击中山坡上的目标A。已知A点高度为h，山坡倾角为θ，由此可算出

( )

图6

A．轰炸机的飞行高度 B．轰炸机的飞行速度

C．炸弹的飞行时间 D．炸弹投出时的动能

【解析】此题属于小球做平抛运动落点在斜面上的类型题。设轰炸机投弹位置高度为H，炸弹水平位移为s，由平抛运动规律有：

图7

【答案】ABC

【感悟】在解答该类问题时，除了要运用平抛运动的位移和速度规律外，还要充分利用斜面倾角，弄清斜面的倾角是隐含速度的方向角还是位移的方向角，从而使问题得到顺利解决。

【例4】如图8所示，斜面倾角为θ，位于斜面底端A正上方的小球以初速度v0正对斜面顶点B水平抛出，小球到达斜面经过的时间为t，重力加速度为g，则下列说法中正确的是

( )

图8

当小球垂直击中斜面时，速度与水平方向的夹角为：

当小球击中斜面中点时，假设斜面长为2L，由平抛运动规律可知：

水平射程为：Lcosθ=v0t

【答案】AB

【感悟】本题主要考查了平抛运动与斜面相结合的问题，此类平抛问题一直是高考或大型考试中的热点。此题涉及小球如何落到斜面上的问题，解决这类问题的关键是充分理解斜面倾角的作用，弄清斜面的倾角是隐含速度的方向角还是位移的方向角，然后根据平抛运动规律及位移或速度的三角函数关系解决问题。

4.落点在曲面上

4.1 模型结构

平抛运动与曲面(圆弧)相结合的模型，其特点是做平抛运动的物体落在曲面(圆弧)上，包括两种情况：(1)物体落在曲面(圆弧)的凸面上，如图9甲所示；(2)物体落在曲面(圆弧)的凹面上，如图9乙所示。

图9

4.2 解题思路与方法

做平抛运动物体的落点在曲面(圆弧)上时，题目通常会给出物体轨迹恰好与曲面(圆弧)相切或恰好从曲面(圆弧)的某点沿圆弧的切线方向进入凹面。我们可以过相切点做辅助线来构造斜面，把落点在曲面(圆弧)上的问题转化为落点在斜面上的问题来求解。按照求解落点在斜面上的平抛运动的方法，利用几何关系找到此斜面的倾角，弄清斜面的倾角是隐含速度的方向角还是位移的方向角，运用平抛运动规律及速度(或位移)的三角函数关系进行解题。

【例5】(2016·上海卷第24题)如图10，圆弧形凹槽固定在水平地面上，其中ABC是位于竖直平面内以O为圆心的一段圆弧，OA与竖直方向的夹角为α。一小球以速度v0从桌面边缘P水平抛出，恰好从A点沿圆弧的切线方向进入凹槽。小球从P到A的运动时间为t=________；直线PA与竖直方向的夹角β=________。

图10

【解析】根据题意，小球从P点抛出后做落点在曲面(圆弧)上的平抛运动，可以过切点A做辅助线来构造斜面，利用几何关系可知此斜面的倾角α是速度的方向角，小球运动到A点时将速度分解，如图11甲所示，则有：

图11

小球从P点到A点的位移三角函数关系(如图11乙所示)：

所以PA与竖直方向的夹角为：β=arctan(2cotα)。

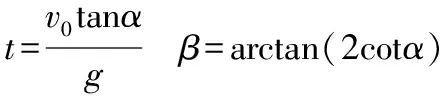
【例6】(2017·辽宁模拟)如图12所示为四分之一圆柱体OAB的竖直截面，半径为R，在B点上方的C点水平抛出一个小球，小球轨迹恰好在D点与圆柱体相切，OD与OB的夹角为60°，则C点到B点的距离为

( )

图12

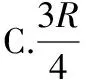
【解析】此题属于小球做平抛运动落点在曲面(圆弧)上的问题，可以过切点D连接OD，从而构造斜面，利用几何关系可知此斜面的倾角30°是速度的方向角。设小球平抛运动的初速度为v0，将小球在D点的速度沿竖直方向和水平方向分解，由速度三角函数关系可知：

小球平抛运动的水平位移为：x=Rsin60°

由平抛运动的规律可知：x=v0t

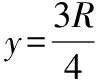
【答案】D

【感悟】此题关键在于构造斜面，把落点在曲面上的问题转化为落点在斜面上的问题，利用几何关系找到此斜面的倾角30°是速度的方向角，运用平抛运动规律及速度三角函数关系解题。

三、教学反思小结

综上可知，解决平抛运动模型问题的一般解题思路和方法是：

1.对于落点在水平面、竖直面上的平抛运动问题，可以将平抛运动看作水平方向的匀速直线运动和竖直方向的自由落体运动的合运动。由于竖直分运动为自由落体运动，则匀变速直线运动的解题方法和技巧都可以使用。

2.对于落点在斜面上的平抛运动问题，可以从斜面倾角θ为切入点，它可能隐含的是位移的方向角，其三角函数关系联系了水平位移、竖直位移和实际位移，也可能隐含的是速度的方向角，其三角函数关系联系了水平速度、竖直速度和实际速度，可见只要找到斜面的倾角隐含的是什么角，也就找到了解决这类问题的突破口。具体解题技巧有以下两个方面：(1)首先根据题目隐含条件的特点，以斜面倾角θ为切入点，弄清斜面倾角是速度方向角还是位移方向角；(2)然后运用平抛运动的基本规律，从合速度(合位移)与分速度(分位移)间的三角函数关系入手求解。