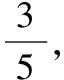动量守恒定律在碰撞问题中的应用
天津 徐海霞
一、碰撞类型
1.解读碰撞
两个物体在极短时间内发生相互作用,且作用力较大,这种情况称为碰撞。
由于作用时间极短,一般都满足内力远大于外力,所以可以认为系统的动量守恒。按碰撞前后物体的动量是否在一条直线上分为正碰和斜碰,中学物理只研究正碰的情况。碰撞又分弹性碰撞、非弹性碰撞、完全非弹性碰撞三种。弹性碰撞是物体在碰撞过程中发生的形变完全恢复,不存在势能的储存,物体系统碰撞前后的总动能相等。完全非弹性碰撞指两物体碰后粘合在一起,发生的形变不恢复,以同一速度运动,机械能损失最大。非弹性碰撞是碰后两物体能分开,动量守恒,但动能有损失,损失的动能转化为热量,动能损失介于弹性碰撞和完全非弹性碰撞之间。
2.三种碰撞类型的分析
如图1所示,光滑的水平面上,有两个质量分别为m1和m2小球A、B,A球以v1的速度与静止的B球发生正碰。

图1
(1)弹性碰撞:碰后分开,动量及动能守恒,有:

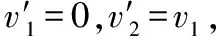
(2)完全非弹性碰撞:碰后粘在一起,动量守恒,动能损失最大,损失的动能转化为内能,有:
m1v1=(m1+m2)v
(3)非弹性碰撞:碰后分开,动量守恒,动能有损失,损失的动能转化为热量。动能损失介于弹性碰撞和完全非弹性碰撞之间,有
下面再通过带弹簧的两个相互作用的物体为例,看看三种碰撞形式。

图2

在整个过程中,可以认为系统不受外力,故系统动量一定是守恒的。由于在整个过程中不好断定弹簧弹性的变化,机械能是否守恒要具体问题具体分析了。
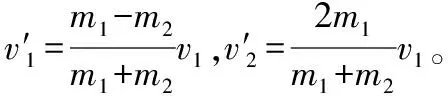

(3)若弹簧不是完全弹性的。在状态a至状态b过程中,系统动能在减少,一部分动能转化为弹簧弹性势能,一部分动能转化为系统内能,状态b系统动能达到最小,弹簧弹性势能仍能达到最大,但数值上比(1)中弹簧弹性势能要小;从状态b至状态c过程中弹簧弹性势能减少,一部分转化为系统动能,一部分转化为系统内能。这种碰撞就是非弹性碰撞。在这一过程中,系统不受外力,故动量守恒,但全过程中系统一部分动能转化为系统内能,故系统动能有损失而不守恒,则机械能不守恒。
综上所述,解决碰撞问题就要把握好系统动量守恒、能量不增加这一原则。
二、例谈碰撞中的动量守恒定律的应用
1.完全弹性碰撞
【例1】质量为m1=1 kg的滑块以6 m/s的速度沿光滑水平面向质量为m2=2 kg的静止滑块运动,并发生正碰。碰后两滑块的速度可能分别是
( )
A.-3m/s,4.5m/s B.-1m/s,3.5m/s
C.3m/s,1.5m/s D.2m/s,3m/s
【解析】解法1:先判断是否符合系统动量守恒,可排除D选项;再判断动能是否增加,可排除A选项;还要判断顺序是否合理,可排除C选项;只有B选项是可能的。
【答案】B
【点评】此类碰撞问题要考虑三个因素:
(1)碰撞中系统动量守恒;
(2)碰撞过程中系统动能不增加;
(3)碰前、碰后两个物体的位置关系(不穿越)和速度大小应保证其顺序合理。
2.完全非弹性碰撞
【例2】设质量为m的子弹以初速度v0射向静止在光滑水平面上的质量为M的木块,并留在木块中不再射出,子弹钻入木块深度为d。求木块对子弹的平均阻力的大小和该过程中木块前进的距离。
【解析】子弹和木块最后共同运动,相当于完全非弹性碰撞。
从动量的角度看,子弹射入木块过程中系统动量守恒:mv0=(M+m)v
从能量的角度看,该过程系统损失的动能全部转化为系统的内能。设平均阻力大小为f,设子弹、木块的位移大小分别为s1、s2,如图3所示,显然有s1-s2=d,则

图3
①②联立解得:
【点评】完全非弹性碰撞要抓住系统动量守恒、但系统机械能损失最多这一特点列式求解。
3.与图象结合的碰撞问题
【例3】质量分别为m1、m2的小球在一直线上做弹性碰撞,它们在碰撞前后的位移—时间图象如图4所示,若m1=1 kg,则m2的质量等于多少?

图4

【答案】3 kg
【点评】本题是一道有关图象应用的题型,关键是理解每段图线所对应的量,求出各物体碰撞前后的速度。注意不要把运动图象的形状同运动轨迹混为一谈。
4.带弹簧的碰撞问题
【例4】如图5所示,质量为m的钢板与直立轻弹簧的上端连接,弹簧下端固定在地上,平衡时,弹簧的压缩量为x0。一个物块从钢板的正上方相距3x0的A处自由落下,打在钢板上并立刻与钢板一起向下运动,但不粘连,它们到达最低点后又向上运动。已知物块的质量也为m时,它们恰能回到O点;若物块的质量为2m,仍从A处自由落下,则物块与钢板回到O点时还具有向上的速度。求物块向上运动所到达的最高点与O点之间的距离。

图5
【解析】由动能定理有,物块与钢板碰撞速度为:
设v1为物块与钢板一起向下的速度,由动量守恒有:mv0=2mv1
设刚碰完时弹簧的势能为Ep,则回到O点时,势能为0,由机械能守恒有:
设v2是质量为2m的物块与钢板碰后的速度,由动量守恒有:2mv0=3mv2
在上述两种情况下,弹簧初始压缩量都是x0,故


【点评】(1)物块与钢板碰撞的瞬间外力之和并不为零,但这一过程时间极短,内力远大于外力,故可近似看成动量守恒。
(2)两次下压至回到O点的过程中,速度、路程并不相同,但弹性势能的改变(弹力做的功)相同。
(3)在本题中,物块与钢板下压至回到O点的过程也可以运用动能定理列方程。

5.需讨论解的碰撞问题
【例5】如图6所示,质量为M的物体P静止在光滑的水平桌面上,另一质量为m(m ( ) 图6 A.Q物体一定被弹回,因为m B.Q物体可能继续向前 C.Q物体的速度不可能为零 D.若相碰后两物体分离,则过一段时间可能再碰 【解析】如果是弹性碰撞,因m 【答案】B 【点评】弹性碰撞和完全非弹性碰撞是碰撞问题的两种极限情况,前者在碰撞结束后物体能完全恢复形变,后者在碰撞结束后完全不能恢复形变,其余的碰撞统称非弹性碰撞,其结果应该是介于两种极限情况之间。对心正碰既不是指弹性碰撞,也不是指完全非弹性碰撞,它是指一维碰撞,即碰撞前后物体在同一直线上运动,显然它既可能是特殊的弹性碰撞或完全非弹性碰撞,也可能是一般的非弹性碰撞。 图7 【解析】设第一个小球与第二个小球发生弹性碰撞后两小球的速度分别为v1和v2,根据动量和能量守恒有: 依次类推,可得第(n+1)个小球被碰后的速度为: 设第(n+1)个小球被碰后对地面的压力为零或脱离地面,则: 联立以上两式代入数值可得n≥2,所以第3个小球被碰后首先离开地面。 【答案】第3个 【点评】解答对于多个物体、多次碰撞且动量守恒的物理过程时,总结出通项公式或递推式是关键。 图8 【解析】子弹穿过A时,子弹与A动量守恒,由动量守恒定律得 mv0=mAvA+mv1① vA=10 m/s ② 子弹穿过B时,子弹与B构成的系统动量守恒,由动量守恒定律得: mv1=mBvB+mv2③ 解得:v2=100 m/s 由③④解得:vB=2.5 m/s ⑤ 子弹穿过B以后,弹簧被压缩,A、B和弹簧所组成的系统动量守恒。 由动量守恒定律得: mAvA+mBvB=(mA+mB)v共⑥ 由功能关系得: 由②⑤⑥⑦解得Ep=22.5 J。
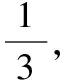


6.碰撞与能量的综合题