随钻用光纤陀螺惯导系统振动误差建模与辨识

王 涛，陈善秋，王 璐，张 林

（1.北京航天时代激光导航技术有限责任公司，北京100094；2.北京航空航天大学仪器科学与光电工程学院，北京100191）

0 引言

定向钻井技术是使井身沿着预先设计的方向和轨迹钻达目的层的钻井工艺方法[1]，井下钻井工具组合利用随钻测量（Measurement while Drilling，MWD）提供定位定向信息[2]。目前，MWD中传统的定向传感器为磁通门与加速度计传感器。磁通门通过敏感地磁场提供井下钻具组合的姿态信息，但是，磁通门易受干扰磁场的影响，导致测量出现偏差[3]。基于光纤陀螺的光纤惯导系统由于具备全自主、抗磁场干扰的优点[4-5]，适用于随钻测量。但是，钻井时的长时间振动环境，会导致光纤陀螺惯导系统出现较大导航误差[6]。因此，急需减小随钻振动环境下光纤惯导系统的振动误差。

目前，针对振动对光纤陀螺以及光纤陀螺惯导系统的影响机理已经进行诸多研究。2004年，北京航空航天大学的宋凝芳等针对数字闭环光纤陀螺振动误差进行了分析[7]。2009年，哈尔滨工业大学的吴磊等利用有限元法对光纤陀螺惯导系统的结构进行分析，从结构上提高了光纤陀螺惯导系统的抗振动性能[8]。2011年，哈尔滨工业大学的舒建涛分析了振动对引起光纤陀螺的弹光效应，详细推导了振动通过弹光效应引起的相位变化和振动之间的数学模型，得出了振动影响下通过光纤的光波会产生附加相位延迟的结论，并提出了抑制振动误差的信号处理方案，改进了解调算法[9]。2015年，北京航空航天大学光电技术研究所的潘雄等为了抑制振动引起的附加相移误差，在保证闭环稳定的条件下，提出了部分解调提前反馈方法，从而抑制了光纤陀螺振动误差[10]。2010年，针对振动中惯导平台误差辨识，文献[11]提出了拓展Kalman滤波方法。2012年与2013年，针对激光惯导在线振动、角振动环境下的误差，进行了分析和研究，文献[12]和文献[13]提出了加速度计交叉耦合项与加速度计二次项误差是振动中的主要误差项。

本文建立了适用于振动环境下的加速度计高阶误差模型，通过误差传播特性分析，提出了加速度计的二次项误差为振动中主要误差项。在此基础上，建立包含加速度计二次项误差的36阶Kalman滤波器，对各项器件误差进行分离、辨识与补偿。

1 MWD用光纤陀螺惯导系统误差模型的建立

捷联惯性测量系统误差源可分为惯性传感器误差、安装误差及导航参数误差等。光纤陀螺和加速度计作为核心传感器组件，其测量误差是光纤陀螺随钻测量系统的主要误差源。研究表明，根据传感器中不同的误差来源，可以建立器件误差模型。在工程应用中经常忽略误差模型中的高阶误差项，仅仅采用1阶误差，即光纤陀螺和加速度计的线性误差模型。光纤陀螺和加速度计线性误差主要由零偏误差、安装误差、标度因数误差及随机误差组成，其误差模型分别为[14]：

Kg和Ka分别为光纤陀螺和加速度计的标度因数误差，Mg和Ma为安装误差系数矩阵，bg和ba分别为光纤陀螺和加速度计零偏误差，分别为光纤陀螺和加速度计的随机误差。在实验室，利用精密位置速率转台可对确定性误差实现标定与补偿，随机误差可以通过误差建模等方式进行抑制。

在随钻测量环境下，由于光纤陀螺惯导系统长时间处于振动等力学环境下，惯导系统导航精度恶化，说明常用的线性误差模型对振动环境中的惯性器件误差不能进行有效补偿。因此，需要建立适用于振动等力学环境下惯性器件误差模型。

考虑光纤陀螺与加速度计的高阶误差项，建立适用于振动环境的光纤陀螺与加速度计的非线性误差模型[15]。由光纤陀螺的常值漂移误差bg、标度因数误差Kg、安装误差Mg、随机漂移误差与二次项误差dg，建立的光纤陀螺非线性模型以及误差模型如下：

考虑加速度计的常值漂移误差ba、标度因数误差Ka、安装误差Ma、随机漂移误差与二次项误差da，建立加速度计非线性模型以及误差模型如下：

2 振动条件下高阶误差项传播特性研究

利用轨迹发生器设定特定的工作状态，产生原始的没有任何误差的光纤陀螺与加速度计仿真数据。然后通过光纤陀螺和加速度计的误差模型，添加单一误差项至原始的光纤陀螺与加速度计数据中。使用带有误差项的数据分别进行静止和振动两种状态下的导航解算，并分别将导航结果与轨迹发生器产生轨迹做差从而得到导航误差。通过比较单一误差项在静止和振动中产生的导航误差，可以得到误差项在两种状态下的传播特性，并且可辨识出振动中的主要误差项。

2.1 振动模型

利用轨迹发生器，在导航坐标系的北向、天向和垂直方向分别存在线振动[16]，其线振动模型为：

其中，A为线振动加速度幅值，取5g；f为线振动频率，取为25Hz。其他条件与静态情况一致。振动中加速度计和陀螺的仿真数据（1s）如图 1所示。

由图1可知，3个加速度计均有振幅为5g，在1s的时间内，正好产生了25个正弦振动周期，因此频率为25Hz。由于载体正弦运动，陀螺输出也围绕在静态输出值下作正弦振动。

2.2 仿真参数设置

仿真过程中设定惯性导航的初始位置为北纬39.9778°，东经116.3434°。初始姿态角信息为：工具面角T＝0°，倾斜角I＝0°，方位角A＝0°，东向、北向、天向初始速度均为0m/s。仿真时间2h，数据更新率200Hz，生成两组仿真数据。

数据1仅加入陀螺二次项误差，惯导系统误差设置为：

数据2仅加入加速度计二次项误差，惯导系统误差设置为：

2.3 陀螺和加速度计二次项误差仿真分析

利用数据1进行导航验证，仿真结果如图2、图3所示。图中按照纬度误差、经度误差、高度误差、倾斜角误差、工具面角误差、方位角误差、东向速度误差、北向速度误差、天向速度误差的顺序排列。蓝线为惯导系统静止时误差的传播特性，红线为惯导系统振动时误差传播特性。

由图2可以看出，在静态下陀螺的二次项误差引起的导航误差非常小，几乎为0。这也是在工程中机动状态比较小的情况下，经常忽略二次项误差的原因。但是，在振动状态下，陀螺的二次项误差导致导航误差变大，东向速度误差、北向速度误差、经度误差和纬度误差有发散趋势。引起的方位角围绕0进行Schlar振荡，且噪声变大。但是1×10－5的二项项系数在线振动条件下引起的导航误差项很小，量级很小。因此，陀螺的二次项非线性系数也不是主要误差项。

由图3可以看出，在静态下加速度计的二次项误差引起的导航误差非常小，几乎为0，在机动状态小的情况下，可以忽略。但是，振动中加速度计的二次项误差引起的导航误差非常大。其中，北向位置误差为50km，东向位置误差达到150km。3个姿态角均产生2100″约0.58°的误差，速度误差最大达到50m/s。说明振动状态下，会激励惯性器件非线性误差项引起的导航误差，非线性误差项不能忽略。比较加速度计二次项误差与加速度计零偏误差引起的导航误差，两者在振动中的导航误差除了量级上的不同，传播趋势完全一致。假设二次项系数为5×10－5s2/m，如果在振动中加速度计持续有 5g的比力输入，5×10－5s2/m×(5×10m/s2)2＝12.5mg，则会产生12.5mg的偏值附加给惯导系统。因此可以得出，二次项误差在振动环境下相当于一个常值零偏，并且振动幅度越大，即给加速度计越大的输入比力，由二次项误差引起的导航误差越大。因此，在振动中采用线性的误差模型，将二次项误差忽略，必将造成较大的导航误差。

通过以上仿真及分析可以得到如下结论：在静态或低动态环境下，与加速度有关的二次项误差往往忽略不计；但当存在线振动时，其引起的导航误差明显变大，不能忽略，必须采取相应措施予以补偿。与角速度有关的二次项误差虽然与静态环境下误差传播特性不一致，但是其引起的导航误差偏小，在振动状态下依然可以忽略。

3 高阶振动误差辨识与补偿

陀螺的输出误差是由输入角速度激励产生的，而加速度计的输出误差是由输入加速度激励产生的。在不同运动的激励信号下，可以实现各个误差的分离与辨识。工程中通常忽略高阶误差项，采用不包含加速度计二次项的33阶误差模型对惯导系统的各项误差进行辨识。当系统的二次项误差不能忽略，就会影响33阶误差模型对器件误差的估计。为了验证考虑加速度计二次项误差的36阶误差模型的准确性，将包含有加速度计二次项误差的高阶误差模型（36阶）与不包含二次项的线性误差模型（33阶）进行对比。

3.1 基于高阶误差模型的Kalman滤波器设计

上节的仿真表明，在线振动环境下，陀螺的二次项误差可以忽略，但是加速度计的二次项误差能够引起显著的导航误差，不能忽略不计，必须采取相应措施予以补偿。因此，在建模时应将加速度计二次项误差考虑在内。将光纤陀螺与加速度计的误差模型重写如下：

式（5）简化为[17]：

bg＝为光纤陀螺零偏误差，为光纤陀螺的随机误差，δkg为陀螺的标度因数与安装误差矩阵。其中，为标度因数误差，为陀螺的安装误差。

式（6）简化为：

离散线性系统的Kalman滤波状态方程可表示为[18]：

其中，Xk是系统的状态向量，Wk－1是系统过程噪声序列，Fk，k-1是系统的状态转移矩阵，Gk-1是噪声输入矩阵。

含有高阶误差项的系统Kalman滤波模型的状态向量为：

状态向量X包含9个导航误差，器件误差包含陀螺加速度计的零偏误差、标度因数误差、安装误差以及加速度计的二次项误差，共36个状态量。

系统噪声为：

将陀螺加速度计激励噪声等效为Gauss白噪声，系统矩阵A（t）为：

其中，δθ为角位置误差，v为导航坐标系下的速度，R为地球半径，δv1为速度误差，h为高度，ψ为姿态误差角，为地球自转角速率，为导航坐标系相对于地球坐标系的角速率，▽n为加速度计零偏，fn、fb分别为载体在导航系和载体系下的比力，为姿态矩阵，εn为陀螺器件误差，gn为重力加速度。

根据陀螺与加速度计的误差模型可知，当Kalman滤波估计出惯性器件的确定性误差参数时，可以按照下式对惯性器件误差进行补偿：

离散线性系统的Kalman滤波量测方程可表示为：

其中，Zk是系统的量测序列，Vk是量测噪声序列，Wk－1和Vk是互不相关的白噪声序列，Hk是量测矩阵。为MWD惯导系统解算出的速度向量，是MWD惯导系统的实际速度，是MWD惯导系是MWD惯导系统的实际位置信息。

3.2 标定路径设置

各误差项在观测量中的反应不同，通过改变运动激励各项误差，可以提高各误差项的可观测程度。激励信号的改变在实验室可以通过转台实现，转台旋转为陀螺提供不同的角速度输入，以此激励陀螺的误差项；转台的姿态变化使加速度计上的重力加速度分量输入不同，以此激励加速度计的误差项，最优的激励方式可以实现各误差项的分离与辨识。标定路径设计如表1所示，初始状态为东北天。

在仿真数据中加入各项误差，陀螺零偏为0.02（°）/h，加速度计零偏为 100μg，陀螺标度因数误差为 1×10－5，陀螺的安装失准角误差为1×10－5rad，加速度计标度因数误差为 5×10－5，加速度计的安装失准角误差为5×10－5rad，加速度计二次项误差为1×10－6s2/m。比较考虑了加速度计二次项误差的36阶误差模型与没有考虑加速度计二次项误差的33阶误差模型对各项误差的辨识的准确性。

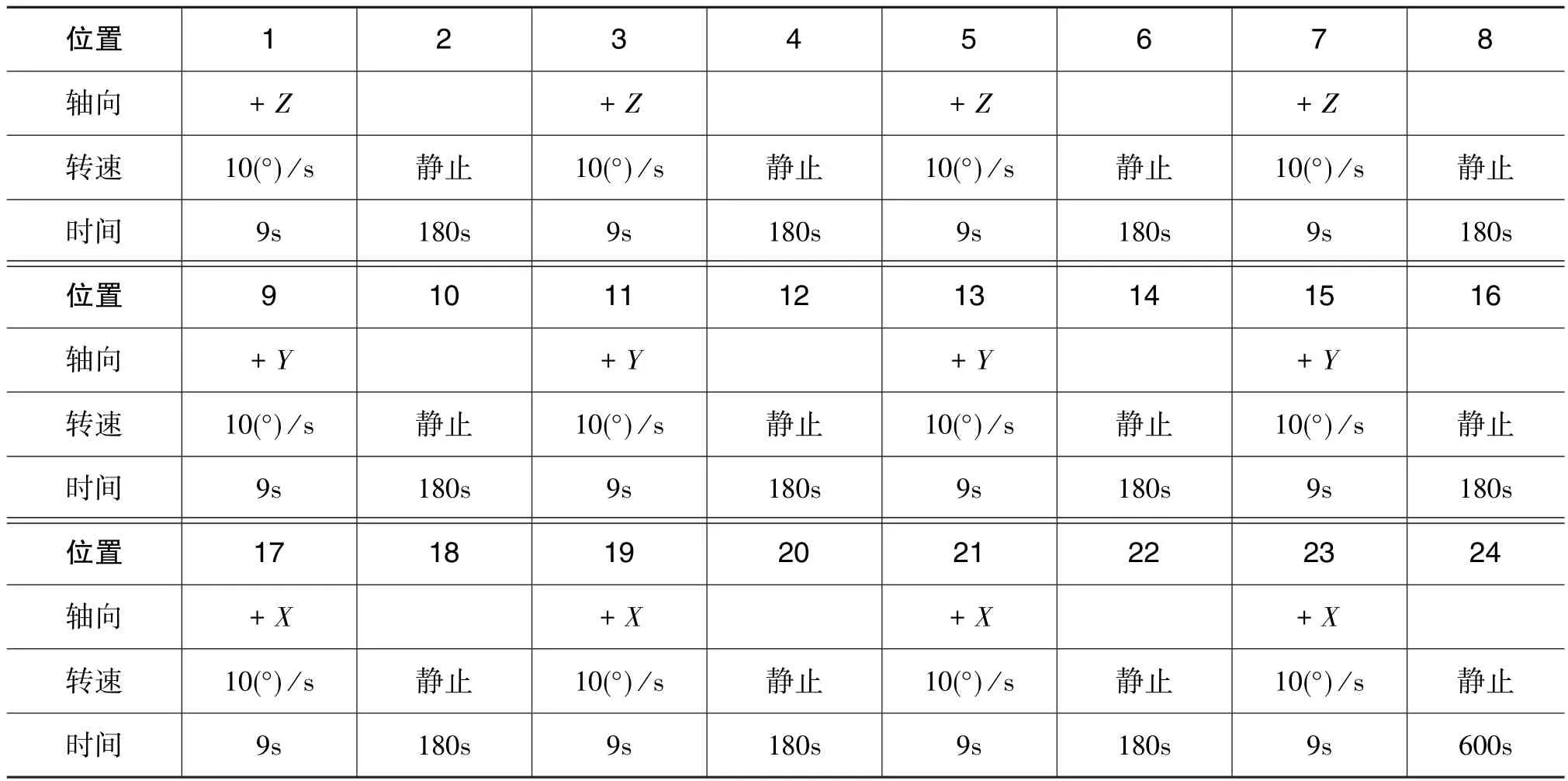
表1 标定路径设计Table 1 Trajectory of the calibration

3.3 高阶误差模型与线性误差模型对比

由图4可知，基于33阶的误差模型的加速度计零偏估计值相对真值偏大，东向陀螺估计值依然偏大，北向陀螺估值没有收敛。但是，36阶模统得到的位置信息，型可以准确估计出传感器零偏。由图5、图6可知，不考虑二次项误差的33阶滤波器不太稳定，标度因数误差与安装失准角误差估计不准确。

为进一步证明加速度计二次项误差的必要性，表2列出了滤波器各个参数的估计值与估计比率。

由表2可知，33阶滤波器估计性能出现了恶化。只有天向陀螺的零偏误差与东向加速度计的标度因数误差项的估计比率达到了90%以上，其他参数估计比率均不理想，并且有7个误差项是估计错误或者不能估计。但是，考虑了二次项误差的36阶滤波器可以辨识二次项误差与零偏误差并将它们分离。其中，加速度计二次项误差估计比率达到了99%，说明了考虑高阶误差项的误差模型的必要性。

综上所述，考虑了加速度计二次项误差的36阶误差模型优于33阶滤波器，误差估计结果更加准确。

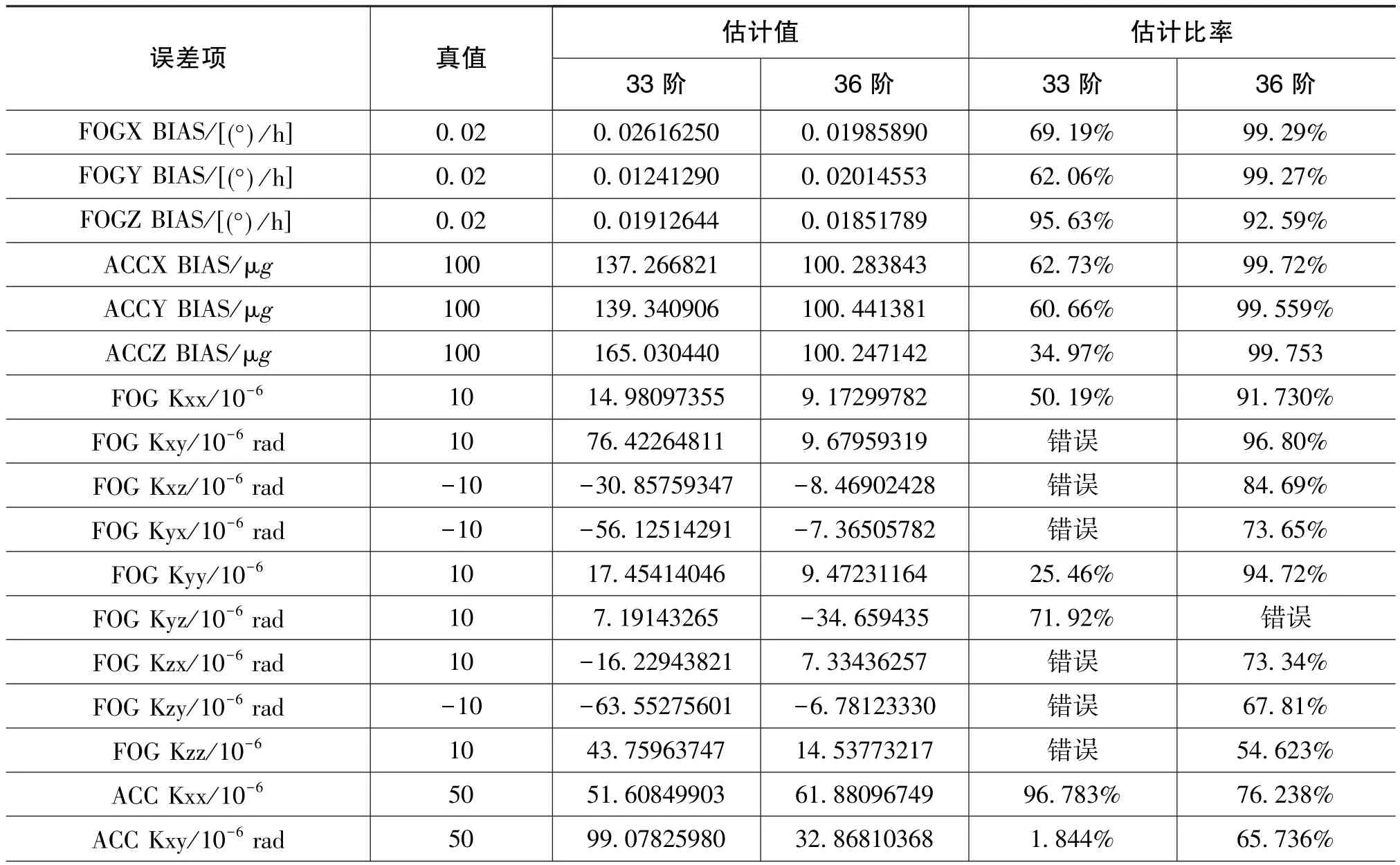
表2 33阶滤波器与36阶滤波器估计结果对比Table 2 Estimation results of the 33 dimension KF and 36 dimension KF

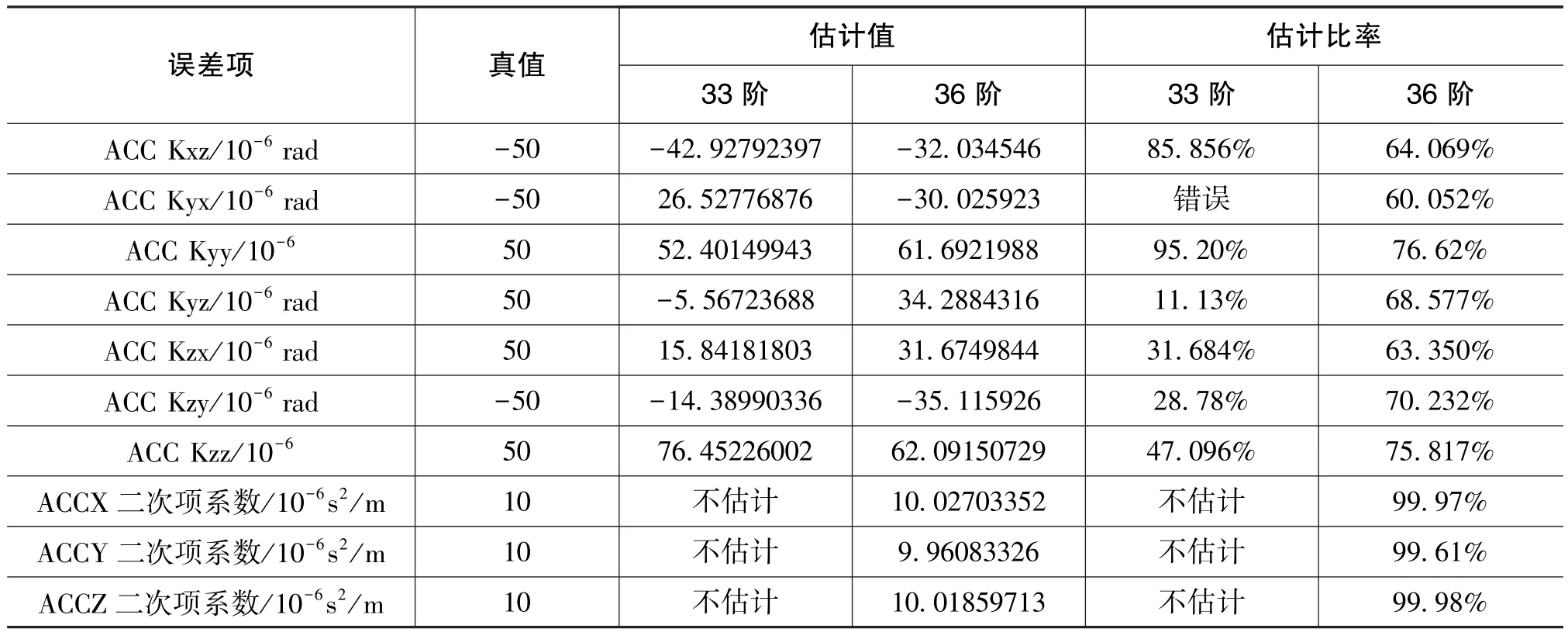
续表

4 线振动仿真试验验证

基于2.1节中的振动模型，利用轨迹发生器生成振动数据。首先静止10min，然后振动70min，最后静止10min。加入误差项如表2第2列所示，在此基础上在传感器数据中加入Gauss白噪声。将36阶滤波器分离出的误差值补偿进数据，一组仅仅补偿线性误差，另一组不仅补偿一次项误差，而且补偿二次项误差。进行纯惯导验证，对比两组不同补偿数据在振动中的导航结果。

首先利用仿真数据前5min进行初始对准，对准结果为：航向角0.096938°，倾斜角0.008627°，工具面角－0.00286°。不补偿二次项的导航结果如图7所示，补偿了二次项误差的导航结果如图8所示。9个导航参数中，速度和位置受线振动影响很大，而线振动又会激励二次项误差，因此二次项误差是线振动中的主要误差。不补偿二次项时，东向速度误差与北向速度误差在振动状态下最大达到50m/s，东向位置与北向位置最大误差达到90000m。其中，姿态角最大误差约为0.7°。而补偿了二次项误差后的导航结果远远优于未补偿二次项误差的导航结果。其中，最大速度误差减小至2.2m/s，纬度误差减小至1000m，经度误差减小至2200m，高度误差也由100m减小至10m，姿态误差最大值减小至0.01°。由此可见，补偿二次项对提高振动中导航精度具有重要的作用。

5 结论

本文提出加速度有关的二次项误差对导航精度的影响，建立适用于振动环境下的高阶器件误差模型，研究了高阶误差模型在振动和静态情况下的传播特性。通过理论分析和仿真计算，得到以下结论：

1）振动环境下，加速度有关的二次项误差将严重影响MWD惯导系统导航精度，必须采取相应措施予以补偿。

2）提出包含加速度计二次项误差的36阶高阶滤波与传统33阶滤波器相比，更能有效估计器件误差，可以辨识二次项误差与零偏误差并将它们分离。其中，加速度计二次项误差估计比率达到了99%，证明了高阶误差项的误差模型的准确性。

3）36阶滤波器辨识出的误差补偿后的导航验证结果表明：补偿了二次项误差之后的导航精度得到明显提高，速度误差由50m/s减小至2.2m/s，位置误差由90000m减小至2000m，姿态误差由0.7°减小至 0.01°。