一种精密离心机误差分析与精度评定方法

王胜利，刘合朋，胡吉昌，钟正虎，张春京

（北京航天控制仪器研究所，北京100039）

0 引言

精密离心机是一种重要的惯导测试设备，主要用于惯导加速度仪表的测试和标定，在航天、航空、船舶、兵器等领域有着广泛的应用[1-4]。精密离心机能够为惯性器件产生较大的向心加速度输入，从而充分激励被试产品的高次项误差模型系数。特别是对于高精度的线加速度计的标定，更需要有高精度的离心机与之配套。随着惯性加速度仪表技术的不断发展，对精密离心机的精度和各项性能要求也越来越高[5-11]。

本文主要通过研究精密离心机的误差模型和各项误差源对离心机给定加速度的影响，目的是找到提高离心机精度的途径，也可以用来对特定离心机进行误差等级的评定。

1 离心机测试的总输入加速度

离心机测试时，被测仪表（加速度计）输入轴（IA）上的输入总加速度ai为：

其中，ac为离心机在被测仪表输入轴上的给定加速度，al为重力加速度在被测仪表输入轴上的分量，ah为地球哥式加速度在被测仪表输入轴上的分量。

因此，被测仪表输入轴上输入加速度的总不确定度为：

2 离心机给定加速度的不确定度

离心机在被测仪表输入轴上给定加速度为：

其中，R为转臂半径，ω为离心机的转速。

从式（1）可得离心机给定加速度相对不确定度为：

其中，δR为半径相对不确定度，δω为转速相对不确定度。

2.1 半径不确定度

（1）静态半径不确定度

静态半径的相对不确定度δR1为：

其中，R0为静态半径（名义半径），即离心机不转动（静止）时，从回转轴线到台面被测仪表安装块基准面之间的距离；ΔR1为静态半径的不确定度。

由于离心机测时，静态半径使用实测值，因此静态半径的不确定度实质为静态半径的测量不确定度。

（2）动态半径的不确定度

离心机转动时，台面会由于惯性力拉伸变长。在离心机测试时，可将台面半径伸长量测出，补偿到静态半径值中。因此，动态半径的不确定度实质为动态半径的测量不确定度。

动态半径测量的相对不确定度δR2为：

其中，Rd为动态半径，即离心机转动时，静态半径伸长量；ΔR2为动态半径测量的不确定度。

（3）温度变化引起的半径不确定度

当离心机在不同于静态半径测量时的温度下工作时，半径可按式（6）计算：

其中，ΔT为工作时与静态半径测量时的温差；α为台面材料的热膨胀系数，台面为铸铁时，α＝1.3×10－5/℃。

当进行离心机测试时，只有准确测出当前的温度值，就可按式（6）将温度变化引起的半径变化量补偿到静态半径值中。因此，由温度变化引起的半径不确定度只由温度测量传感器的测量精度Δt决定，其相对不确定度为：

（4）半径的总不确定度

离心机半径的相对总不确定度δR为：

2.2 转速不确定度

（1）转速精度不确定度

离心机转速精度定义为离心机转速的实际值与名义值之间的差值。转速测量一般采用定角测时方法，即利用计数器测量离心机转动一圈所需的时间，可计算出离心机的实际转速。

离心机转速ωi为：

其中，ti为第i次的时间测量值；n为记录的次数，n＝10。

将同一转速指令下的n次转速值求平均，得平均转速：

在名义转速ω下，转速精度相对不确定度可以按照式（9）计算：

（2）转速稳定性不确定度

离心机转速稳定性定义为离心机长时间通电转动时转速的稳定程度，测量方法同转速精度测量方法。如离心机在每个速率值连续运行10min，每分钟记录一组时间值，每组10个数据，共记录6组。

将同一组转速指令下的n次转速值求平均，得本组的转速平均值：

同一转速指令下，N组测量值求平均：

其中，N为测试的组数，在示例中N＝6。

转速稳定性相对不确定度：

（3）转速重复性不确定度

离心机转速重复性定义为离心机一次通电，多次启动时，转速的一致程度，测量方法同转速精度测量方法。让离心机在每个速率值连续运行10min，每个速率值重复启动6次，待转速稳定后开始记录，每个转速下10个数据为一组，共记录6组。

将同一转速指令下每组的n次转速值求平均，得本组的转速平均值：

同一转速指令下，N组测量值求平均：

转速重复性相对不确定度：

（4）转速的总不确定度

离心机转速的相对总不确定度δω为：

3 失准角对被测仪表输入加速度的影响

3.1 水平失准角对被测仪表输入加速度的影响

离心机被测件安装块在台面上的布置如图1所示[9]。理想状态下，被测件安装块基准面的法线应指向离心机回转轴线。

离心机静态水平失准角φ0h定义为：当离心机不转动时，在水平面内，被测件安装块基准面的法线与离心机半径方向的偏角。

离心机动态水平失准角φdh定义为：当离心机转动时，静态水平失准角φ0h的变化量。

当离心机转动时，总的水平失准角φh为：

由于水平失准角的存在，离心机在被测仪表输入轴上的给定加速度变为：

其中，ai为被测仪表输入轴上的输入加速度，ac为离心机的给定加速度。

由于φh的值很小（一般为几个角秒），cosφh≈1，因此水平失准角φh对被测仪表输入轴输入加速度的影响可以忽略。

3.2 垂直失准角对被测仪表输入加速度的影响

（1）定义

离心机静态垂直失准角φ0v定义为：当离心机不转动时，在垂直面内，被测件安装块基准面的法线与离心机半径方向的偏角。

离心机动态垂直失准角φdv定义为：当离心机转动时，静态垂直失准角φ0v的变化量。

当离心机转动时，总的垂直失准角φv为：

（2）垂直失准角对被测仪表输入加速度的影响

由于垂直失准角的存在，离心机测试时，仪表输入轴上的输入加速度变为：

其中，gl为当地的重力加速度。

由于φv的值很小（一般为几个角秒），cosφv≈1，因此垂直失准角φv对离心机给定加速度的影响可以忽略。

假设当φv＝5″时，sinφv＝2.4×10－5，可见glsinφv项对被测仪表输入加速度的影响较大，但其对被测仪表输入加速度的影响随离心机给定加速度的增大而减小。离心机测试时，只要准确测得φv的大小，就可以将该项作为零偏项在加速度计测试中扣除。因此，glsinφv项对被测仪表输入加速度不确定度的影响只由φv的测量不确定度决定，即：

其中，δφ为垂直失准角测量引起的被测仪表输入加速度的不确定度，Δφv为垂直失准角的测量不确定度。

（3）静态垂直失准角测量引起的不确定度

在不考虑测量方法系统误差的情况下，静态垂直失准角测量误差只由测量仪器（一般为电子水平仪）的精度决定。

静态垂直失准角测量误差引起的被测仪表输入加速度相对不确定度为：

其中，Δφ0v为静态垂直失准角的测量不确定度，等于测量仪器（电子水平仪）的精度。

（4）动态垂直失准角测量引起的不确定度

动态垂直失准角测量误差引起的被测仪表输入加速度相对不确定度为：

其中，Δφdv为动态垂直失准角的测量不确定度。

（5）垂直失准角测量引起的不确定度

垂直失准角测量在被测仪表输入轴上引起的输入加速度相对不确定度为：

4 回转轴线铅垂度引起的不确定度

4.1 定义

由于离心机的回转轴线与铅垂线不平行，会导致在被测仪表输入轴上引入一个重力分量：

其中，aγ为回转轴线铅垂度引入的重力分量，γ为回转轴线铅垂度，ω为离心机的转速。

4.2 对被测仪表输入加速度的影响

由式（21）可知，aγ的大小随离心机的转动速率周期变化，且在一圈内是零均值的。在测试时，可通过对加速度计一圈内采样值求平均的方法基本消除该项的影响。并且随着离心机给定加速度的增大，此项误差对被测仪表输入加速度的相对不确定度逐渐减小。消除该项后，在精密离心机总误差评定时，此项可不再计入。

在不对此项误差进行修正时，回转轴线铅垂度γ引起的输入加速度最大相对不确定度δγ为：

例如，当离心机轴线铅垂度为2″时，在不同给定加速度ac下，δγ的值如表1所示。

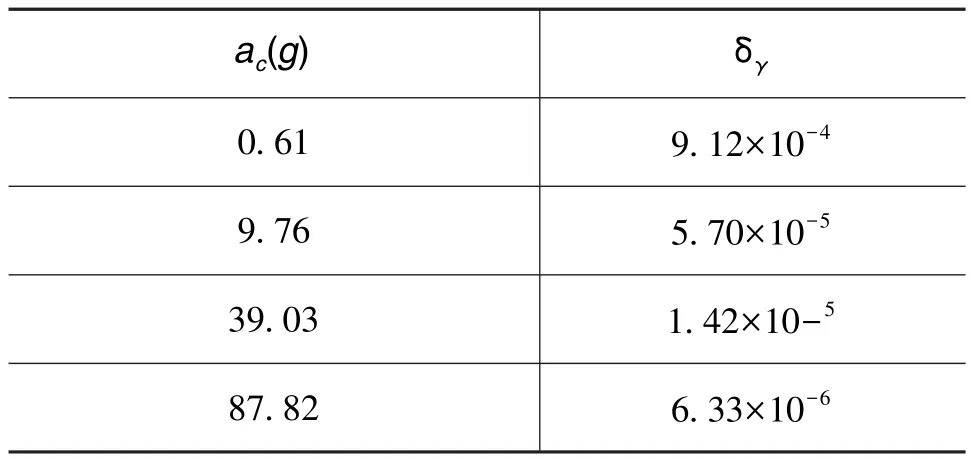
表1 不同给定加速度下δγ的值Table 1 δγin different indicated acceleration

由表1可知，δγ的值在离心机给定加速度较小时影响显著，因此在试验中必须通过整圈采样予以消除。

5 地球哥式加速度引起的不确定度

5.1 定义

在地球表面运动的物体，会受到地球哥式加速度的影响。离心机测试时，由地球转速的垂直分量在离心机半径方向引起的哥式加速度ah为：

其中，ω为离心机的转速，R为离心机的转臂半径，Ωv为当地低速的垂直分量。

5.2 对被测仪表输入加速度的影响

在精密离心试验中，不管要求的给定加速度为正或负，离心机一般都是按同样的方向转动，因此ah的方向总是沿半径方向指向或背离（根据转速方向）离心机回转中心线的方向。其值可以根据式（23）计算出来，并从离心机给定加速度中扣除。

因此，地球哥式加速度对被测仪表输入加速度的影响只由ah的计算误差引起。由于测试地点的Ωv为一固定值，故其值由ω和R的不确定决定。

对式（23）全微分得：

地球哥式加速度计算误差引起的被测仪表输入加速度的不确定度δh为：

其中，δR为半径的相对不确定度，δω为转速的相对不确定度。

由于ΩvδR和Ωvδω均为2阶小量，因此，地球哥式加速度计算误差对被测仪表输入加速度的影响可以忽略。

6 离心机总的不确定度评定方法

离心机在被测仪表输入轴上输入加速度总的相对不确定度为：

其中，δR为离心机半径相对不确定度，δω为离心机转速相对不确定度，δφ为离心机垂直失准角引起的相对不确定度，δγ为离心机回转轴线铅垂度引起的相对不确定度。

7 离心机总的不确定度评定实例

按照上述方法，对某型精密离心机进行了精度评定（由于采用了整圈补偿测试方法，δγ项的影响不再考虑），结果如表2所示。

表2 精密离心机精度评定结果Table 2 Result of precision evaluation of precision centrifuge

在该离心机上对多型线加速度计进行了试验，试验数据结果与评定结果相当。

8 结论

精密离心机作为高精度过载测试设备，其误差模型比较复杂。通过分析各项误差源对仪表输入加速度的影响，可在离心机设计时根据最终精度要求分配各项误差。为进一步提高离心机的精度，单纯地控制各项误差的量级比较困难，而较为简单和实用的方法则是将每一台设备的各项误差值测量出来，只要这些误差值可测并且相对稳定，就可以将测量误差补偿到误差模型中。对应设备研制方，也可通过上述方法对精密离心机给定加速度精度进行评定。