基于FCM聚类的自适应彩色图像分割算法
胡学刚,段 瑶
(1.重庆邮电大学 通信与信息工程学院,重庆 400065;2.重庆邮电大学 系统理论与应用研究中心,重庆 400065)
0 引 言
图像分割[1]方法主要有基于直方图阈值的方法[2]、基于边缘检测的方法[3]、基于区域的方法[4]、基于聚类的方法[5]等。在聚类方法中,模糊c-均值聚类(FCM)算法引入了模糊的概念,能较好表达和处理不确定性问题,是目前应用最广泛的图像分割方法之一。
FCM算法基于特征的相似性构建目标函数,然后通过最小化目标函数实现图像分割。传统FCM算法仅考虑图像像素的灰度信息,忽略了图像的空间邻域信息,在处理含有噪声的图像时分割效果并不理想。于是,研究者们通过在FCM算法中引入像素间的领域信息对其做了一系列的改进[6-8]。然而,这些算法不能自适应地选择参数,影响其应用。Krinidis等[9]引入模糊因子的概念,提出了模糊局部信息c-均值聚类算法(FLICM算法)。该算法能自适应地决定像素的空间和灰度关系,在一定程度上可达到对噪声的鲁棒性和图像细节信息间的平衡。然而,这些算法初始化时都由人工确定聚类个数且随机确定初始聚类中心,容易出现误分割和分割结果不稳定的情况。
由于彩色图像本身的复杂性,选择合适的聚类个数和初始聚类中心更加困难。因此,自适应地确定聚类个数和初始聚类中心成为彩色图像分割的关键问题。近年来,学者们对其开展了不少的研究。例如,文献[10]提出的直方图阈值模糊c-均值混合算法(HTFCM算法)应用直方图阈值方法得到彩色图像中颜色特征一致的区域,然后用FCM算法来提高区域间的紧凑性。文献[11]利用区域分裂合并模块自适应地确定聚类个数和初始聚类中心,由此提出了基于聚类的自适应RFHA算法。文献[12]通过二次分水岭方法获取图像的封闭区域,将各区域的质心作为FCM算法的初始聚类中心,从而提出了一种彩色图像分割的初始化方法。以上这些自适应彩色图像分割算法都存在噪声鲁棒性差、分割效果不够好的缺陷。
针对以上问题,本文提出一种基于FCM聚类的自适应彩色图像分割算法。该算法首先通过直方图阈值方法和区域分裂合并方法得到聚类个数和初始聚类中心,然后使用一种结合像素空间邻域信息的FCM算法对图像进行聚类分割。实验结果表明,所提出的算法不仅能自适应地获得较准确的聚类个数和初始聚类中心,而且明显提高了算法的分割精度和对噪声的鲁棒性。
1 FLICM算法概述
为了合理利用图像像素的局部空间信息,FLICM算法引入了一种同时考虑邻域像素间的空间距离和灰度信息的模糊因子。在给定图像中,对于第i个像素,定义其模糊因子Gki如下
(1)
式中:i是局部窗的中心像素点,Ni表示以像素i为中心的邻域窗,j表示邻域窗Ni中的像素点,dij表示像素i与其邻域窗内像素j之间的欧式距离,ukj表示第j个像素点对第k个聚类中心的隶属程度,m是权重指数(一般取2),vk表示第k个聚类中心。
将模糊因子Gki引入到FCM算法的目标函数中,得到FLICM算法的目标函数为
(2)
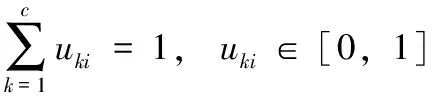
(3)
(4)
从式(1)可看出,模糊因子通过一种模糊的方式把邻域像素间的灰度信息和空间距离进行了融合,邻域像素在模糊因子中所发挥的作用依赖于其与当前像素之间的距离,与当前像素的距离越近,其作用越大。这种方法利用了原始图像,不需要引入任何参数,还可在一定程度上避免损失图像细节信息。
2 本文算法
FCM算法对初始条件的依赖性较大:聚类个数选择不合适会使分割结果出现分类错误情况;初始聚类中心选择不当会导致算法在局部极值处收敛,每次分割可能得到不同的分割结果。此外,现有基于FCM聚类的彩色图像分割算法大多没有考虑像素间的空间邻域信息,图像分割结果容易受到噪声的影响。
根据以上分析,本文使用一种初始化方法,并引入图像像素间的空间邻域信息,由此提出一种基于FCM聚类的自适应彩色图像分割算法。该算法首先通过直方图阈值方法确定彩色图像各颜色分量直方图的分割阈值;然后利用区域分裂合并自适应地得到聚类个数和初始聚类中心;最后用基于像素空间邻域信息的FLICM算法得到最终分割结果。
2.1 确定分割阈值
在RGB颜色空间中,彩色图像的每一个像素点的颜色都由红、绿、蓝这3个颜色通道的强度值混合得到,RGB各分量直方图可以表示整个彩色图像的信息。图像中的均匀部分会在其直方图中形成明显的波峰区域,两相邻波峰区域之间的波谷点可作为各均匀部分之间的分割阈值。寻找各分量直方图分割阈值的具体步骤如下:
步骤1 分别获取给定彩色图像RGB分量的直方图;
步骤2 用如下均值滤波器对每个颜色分量的直方图进行平滑处理,以去除毛刺
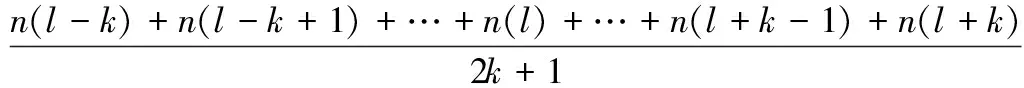
(5)
这里n(l)表示各颜色分量直方图中强度值为l的像素数量,s(l)表示该直方图滤波后在强度值为l处的像素数量,k为邻域半径,通常取2。
步骤3 搜索波峰区域及其峰值;
一个波峰区域An应包括上坡段、下坡段和峰值,可通过连续增长(下降)的数量来判断上(下)坡段。当直方图的强度值连续超过5次增长(下降)就认为是上(下)坡段。若连续增长(下降)不超过5次,重新开始计数。直方图开始(结束)时,如果没有检测到上(下)坡段,只检测到了下(上)坡段,判定其为波峰区域,起始位置为直方图(上坡段)的起点,终止位置为下坡段(直方图)的终点。
取每个波峰区域的重心作为其峰值,第n个波峰区域An的峰值pn的计算公式如下
(6)
步骤4 在直方图中依次取相邻峰值间的最小值作为分割阈值vn。
2.2 区域分裂合并
在彩色图像中,一个均匀区域内的像素点在每一个颜色通道都有一个强度范围。利用2.1节得到的分割阈值vn将彩色图像分裂成若干个区域块,如图1所示。每个区域块表示图像中颜色相似的像素点的集合,这些区域块的端点由各颜色通道上的分割阈值确定。
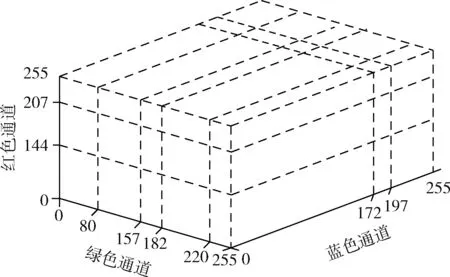
图1 分裂成若干个区域块
通过区域分裂得到的区域块的个数即聚类个数n,该聚类个数往往很大,不适合后期处理。为了得到合适的聚类个数,需要合并视觉上颜色相似的区域。通常用两聚类中心之间的曼哈顿距离来度量其颜色相似性[11]。任意两聚类中心之间的曼哈顿距离定义如下
D(cj,ck)=|Rj-Rk|+|Gj-Gk|+|Bj-Bk|, ∀j≠k
(7)
式中:Rx、Gx、Bx分别为聚类中心cx各颜色分量的颜色值(x=j,k)。当两聚类中心之间的曼哈顿距离小于91时,视觉观察效果为同一种色系。因此,本文设置曼哈顿距离的阈值d为91来合并视觉上颜色相似的区域块,得到最终聚类个数。合并过程具体步骤如下:
步骤1 计算每个区域块内所有像素点的颜色均值,得到初始聚类中心
(8)
式中:1≤j≤n;pj表示属于第j个聚类中心的像素点的个数,pj>0;Xj表示属于第j个聚类中心的像素点集合;xi表示集合Xj中第i个像素的颜色值。
步骤2 利用式(7)计算任意两个聚类中心之间的曼哈顿距离。
步骤3 找到任意两个聚类中心之间的最短曼哈顿距离,如果该距离小于阈值d,将这两个聚类中心所在的区域块合并成一个新的区域块,并用式(8)更新聚类中心。否则,停止合并过程。
步骤4 减少聚类个数n到n-1,执行步骤2,直到两个聚类中心之间的最短曼哈顿距离不小于阈值d。
2.3 基于FCM聚类算法的图像分割
使用式(2)作为目标函数,并利用2.2节得到的聚类个数和聚类中心,迭代得到本文算法的分割结果。其步骤如下:
步骤1 计算聚类个数和初始聚类中心;
步骤2 设置算法结束阈值ε,迭代次数b=1,加权指数m,像素的邻域窗大小w×w;
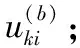
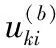
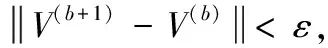
3 实验结果与分析
为验证本文算法的有效性,本节将本文算法与HTFCM算法、RFHA算法进行对比实验,并对实验结果进行主观视觉对比分析和客观指标值比较。实验平台为Win7操作系统,Intel(R) Celeron(R) E3400处理器,主频2.60 GHz,内存3.00 GB,Matlab R2012a。本文算法涉及到的参数:d=91,m=2,ε=0.001,邻域窗大小取3×3。其它算法的参数按相关文献选取。
首先,选取Moon图像为实验对象。图2(a)为原始图像,该图属于夜晚拍摄,由于亮度原因,天空部分存在光照不均匀现象。图2(b)~图2(d)分别为HTFCM算法、RFHA算法及本文算法的分割结果。从图2可看出,HTFCM算法将月亮和天空划分成同一类,出现分类错误情况;RFHA算法受光照不均的影响,将天空分割成两部分;而本文算法受光照不均的影响较小,正确地将整个图像分割成3类:天空、月亮及树木,与实际结果吻合。

图2 Moon的分割结果对比
其次,以Airplane图像作为实验对象。图3(a)为原始图像,显然,Airplane本身与背景应各分为一类。图3(b)~图3(d)分别为HTFCM算法、RFHA算法及本文算法的分割结果。从图3可看出,HTFCM算法与RFHA算法无法将背景聚为一类;而本文算法克服了这一缺陷,将Airplane本身与背景各分为一类,与预期结果相符。

图3 Airplane的分割结果对比
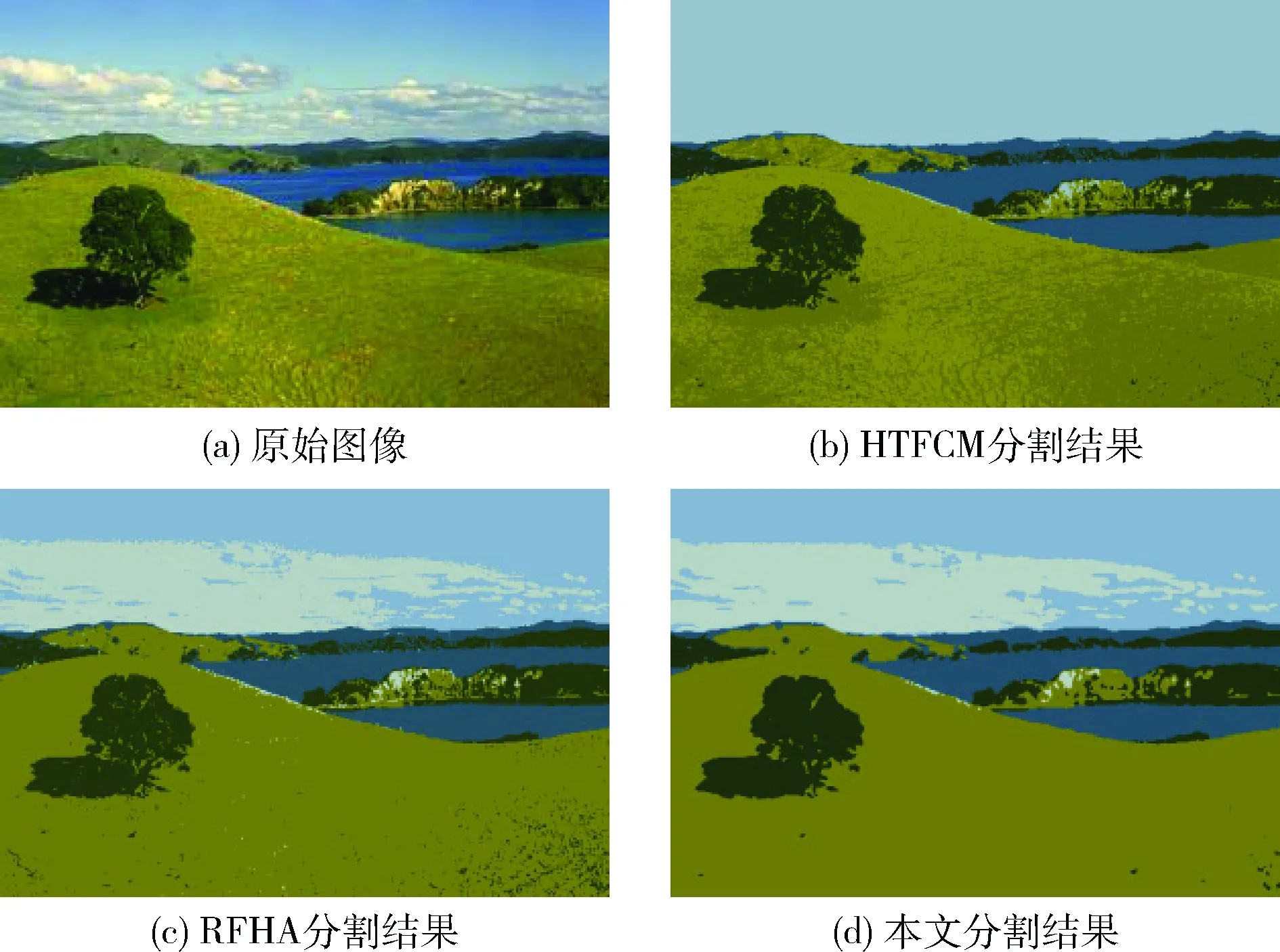
图4 Scenery的分割结果对比
再次,将Scenery图像作为实验对象。图4(a)为原始图像,该图是一幅包括山、水、树、天空和白云的风景画,图像较复杂,并且草坪颜色分布很不均匀,增加了分割的难度。图4(b)~图4(d)分别为HTFCM算法、RFHA算法及本文算法的分割结果。从中可看出,HTFCM算法将应分为两类的天空和白云误分为同一类,且没有将草坪分为一个均匀的区域;RFHA算法的分割结果较HTFCM算法有所改善,但草坪右下角存在很多小的过分割区域;而本文算法将图像各个部分分割清楚,几乎不存在错误分割情况。
最后,以House图像作为实验对象。图5(a)为原始图像,该图屋顶和墙壁存在较多纹理且颜色分布不均匀,图5(b)~图5(d)分别为HTFCM算法、RFHA算法及本文算法的分割结果。从图5可看出,HTFCM算法和RFHA算法的分割结果中,屋顶和墙壁都存在较多小的过分割区域;本文算法的分割结果中,墙壁和屋顶的分割效果都比前面两种算法理想。

图5 House的分割结果对比
此外,为验证本文算法的抗噪性能,这里在以上4幅图像中均加入密度为0.01的椒盐噪声,并分别对噪声图像进行分割对比实验。从图6~图9可看出,HTFCM算法与RFHA算法几乎没有抗噪能力,噪声的加入导致分割结果中出现很多点状的过分割区域;而本文算法引入了像素的空间邻域信息,分割结果与未加噪声图像的实验结果基本一致,达到了很好的抗噪效果。

图6 加噪声Moon的分割效果

图7 加噪声Airplane的分割效果

图8 加噪声Scenery的分割效果

图9 加噪声House的分割效果
由于图像分割结果与人的主观观测意图有很大关联,自然图像分割结果往往不唯一。为了客观评价本文算法的分割效果,这里采用分离系数Vpc[13]与分割熵Vpe[13]这两个客观指标对其定量评价,其评价准则是Vpc值较大时,分割效果较好;Vpe值较小时,分割效果较好。Vpc和Vpe的定义如式(9)和式(10)
(9)
(10)
这里c为聚类个数,n为图像中像素点的总数,uki为第i个像素点对第k个聚类中心的隶属程度。
表1和表2分别是3种分割算法在未加噪声和加噪声时的分离系数与分割熵的比较。从中可看出,本文算法在每一个图像的分割中都得到最优的客观指标值,与主观分析结果一致。因此,本文算法无论是处理未加噪声图像还是处理噪声图像,分割结果都明显优于HTFCM算法与RFHA算法。
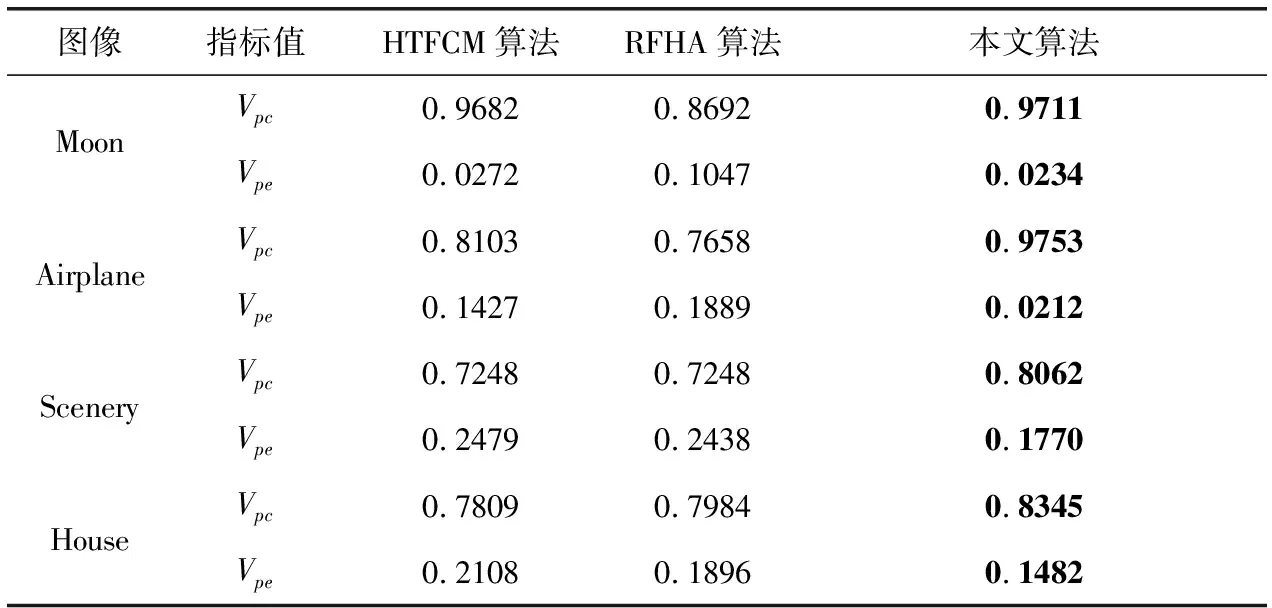
表1 3种分割算法在未加噪声时的分离系数(Vpc)与分割熵(Vpe)的比较
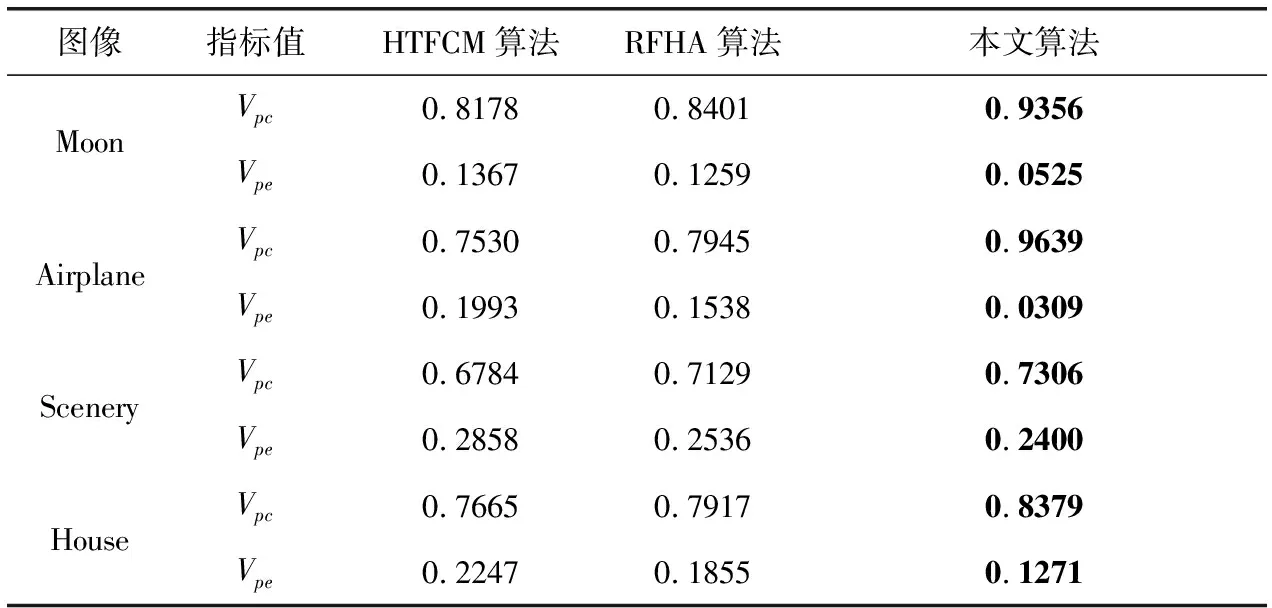
表2 3种分割算法在加噪声时的分离系数(Vpc)与分割熵(Vpe)的比较
4 结束语
本文提出了一种基于FCM聚类的自适应彩色图像分割算法。首先利用直方图阈值和区域分裂合并方法得到较准确的聚类个数和初始聚类中心;然后利用模糊局部信息c-均值聚类算法进行聚类分割,既提高了区域间的紧凑性,也解决了现有FCM算法没有利用空间邻域信息的问题,使算法对噪声具有一定的鲁棒性、区域的均匀性更好,分割结果与人的视觉具有良好的一致性。

