面向配电网的异构无线网络接入选择算法
向 敏,高 盼,杜延红
(重庆邮电大学 工业物联网与网络化控制教育部重点实验室,重庆 400065)
0 引 言
当前的配电网[1,2]通信方式主体采用光纤通信,辅以宽带无线的通信方式。受环境条件限制,在部分地区进行光纤铺设、维护管理时会面临难度大、成本高的问题,且单一无线网络难以满足多种业务的传输需求。因此如何为配电通信业务选择合适的无线通信网络接入成为亟待解决的问题。目前,异构无线网络接入选择的相关研究已取得一定成果,文献[3]提出以灰色关联分析为主要决策方法的网络选择算法,综合考虑影响网络选择的因素,选出优化的网络接入选择方案,能够合理分析网络资源并有效降低接入成本。文献[4]通过将逼近理想解排序和其它不同求解权重的方法相融合,综合考虑接收强度、可用带宽、负载等因素,分别采用层次分析法、熵权法计算各网络参数的权重值,利用TOPSIS对候选网络排序并选择更为合适的网络。文献[5,6]以遗传算法为基础对接入选择方法进行改进,借助于遗传算法的进化特性有效解决了全局寻优的问题。总体来看,灰色关联在系统方案的整体评判上存有一定的不足;TOPSIS法不能很好地反映候选网络内部变化趋势与理想网络之间的异同;遗传算法决策时的可靠性和复杂度有待改善。为此,提出一种基于相对贴近度的智能配电异构无线网络接入选择算法。该算法分别从位置和形状相似性的角度出发,针对候选网络与理想网络之间的接近程度,计算出它们的欧式距离以及灰色关联度,同时结合两者构造出一种新的贴近度即相对贴近度,进而以此为依据对候选网络进行优劣排序,选择出最合适的网络。
1 智能配电异构通信网络模型
智能配电通信系统可采用自建专网或租用公网的方式实现通信[7]。骨干层存在于配电主站和配电子站之间,因该层具有传输数据量大的特点且对传输的可靠性具有较高的要求,通常采用光纤通信技术或其它专网通信技术;接入层形成于配电终端与配电子站(主站)之间,由于配电终端节点数量大、分布范围广且分散、密度不均匀,从而不易使用有线或者单一无线通信实现对终端的全覆盖,因此对光纤铺设、维护难度较大或部分改造工程较复杂的地区可构建多种无线接入技术共存的应用模型。本文所构建的智能配电异构无线接入网络模型如图1所示。
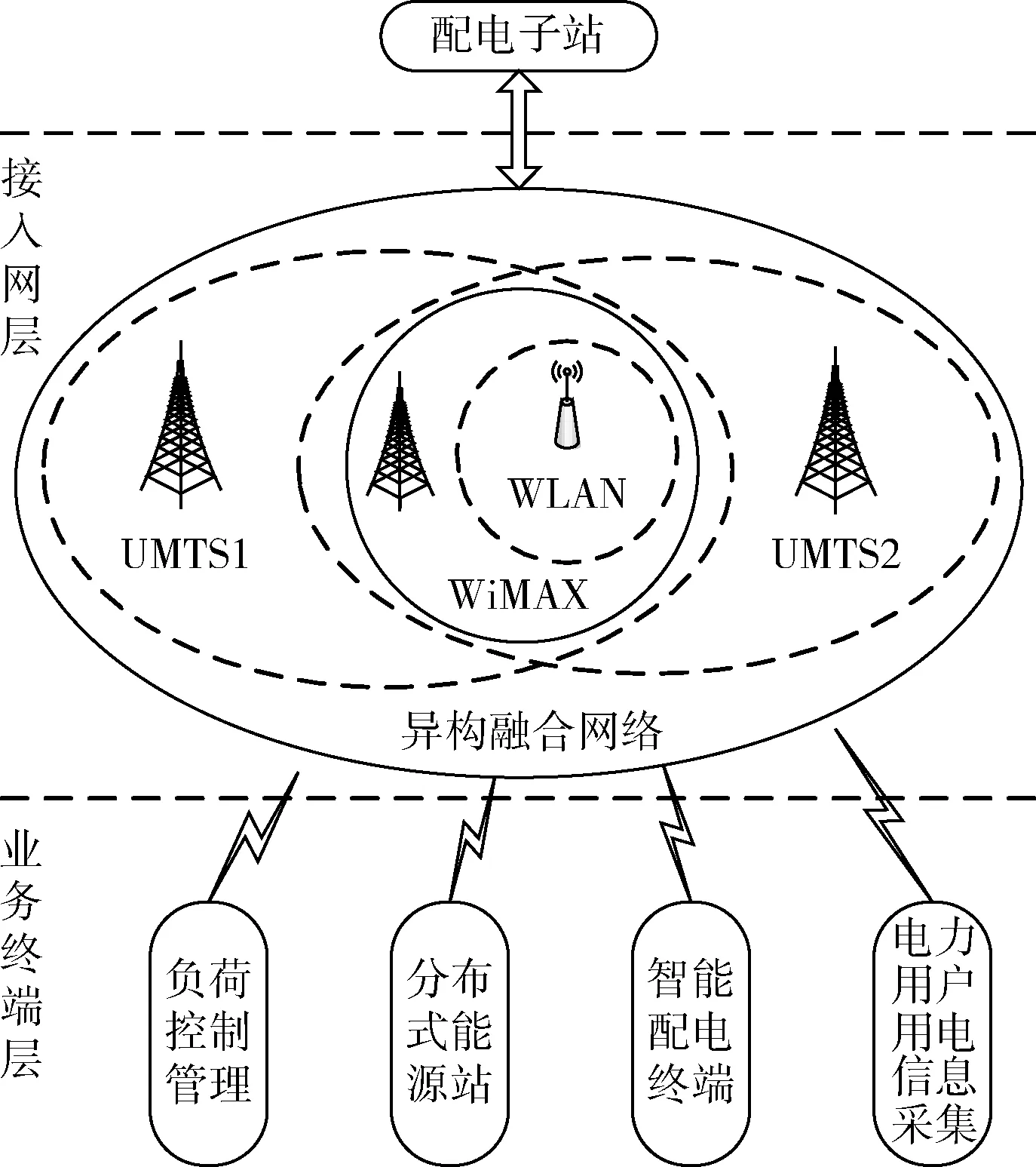
图1 智能配电异构网络模型
智能配电通信系统中存在多种不同类型的业务,从业务功能属性的角度出发,可分为控制型、保护型、信息监测型和视频监控型4种类型,且保护型和控制型比信息监测型和视频监控型更为重要。受业务自身特点的影响,各类业务对带宽、时延、抖动、丢包率,可靠性等服务质量需求不同,表1是4种配电业务类型的需求参数说明[8]。
在智能配电异构网络的覆盖范围内,配电终端结合业务本身特点和实际需求,根据当前各接入网络的实际性能,针对性地选择最适合当前业务正常运行的网络,使得网络资源得到充分利用,同时避免了单一网络覆盖情景下,因网络承载过重的负荷而造成网络拥塞、业务运行不畅等现象。

表1 4种配电业务类型参数说明
2 智能配电异构无线网络接入选择算法
2.1 灰色关联分析和TOPSIS理论
选择合适的网络需要同时考虑网络因素的内在特性和各因素之间的相互作用,对候选网络进行综合评估。为实现业务最终选择最合适的网络接入,采用计算量小,简单方便的灰色关联度和TOPSIS相融合的方法来进行决策。
灰色关联分析以各指标的样本数据为基础,利用灰色关联度表示指标在大小、次序等方面的联系紧密程度,即比较数据序列曲线之间的相似程度。相似程度越高,变化趋势就越相近,关联度就越大。
TOPSIS是一种空间统计学的方法,其基本思想是:分别计算各候选方案距离最好方案与最坏方案的欧氏距离,将其构造成贴近度,进而以所求贴近度作为衡量方案优劣的标准。
2.2 算法整体流程
针对传统TOPSIS法不能很好地体现候选网络内部各因素变化趋势与理想方案之间的差异性问题,本文首先利用层次分析法和反熵权法分别求取业务偏好的主观权重和网络性能的客观权重,结合主客观权重求得综合权重并构建加权标准化矩阵,然后分别求解候选网络与理想网络之间的灰色关联度和欧式距离,将所求灰色关联度和欧式距离构造成相对贴近度,最后以所得相对贴近度为依据进行合适网络的选取。基于相对贴近度的智能配电异构无线网络接入选择算法流程如图2所示。
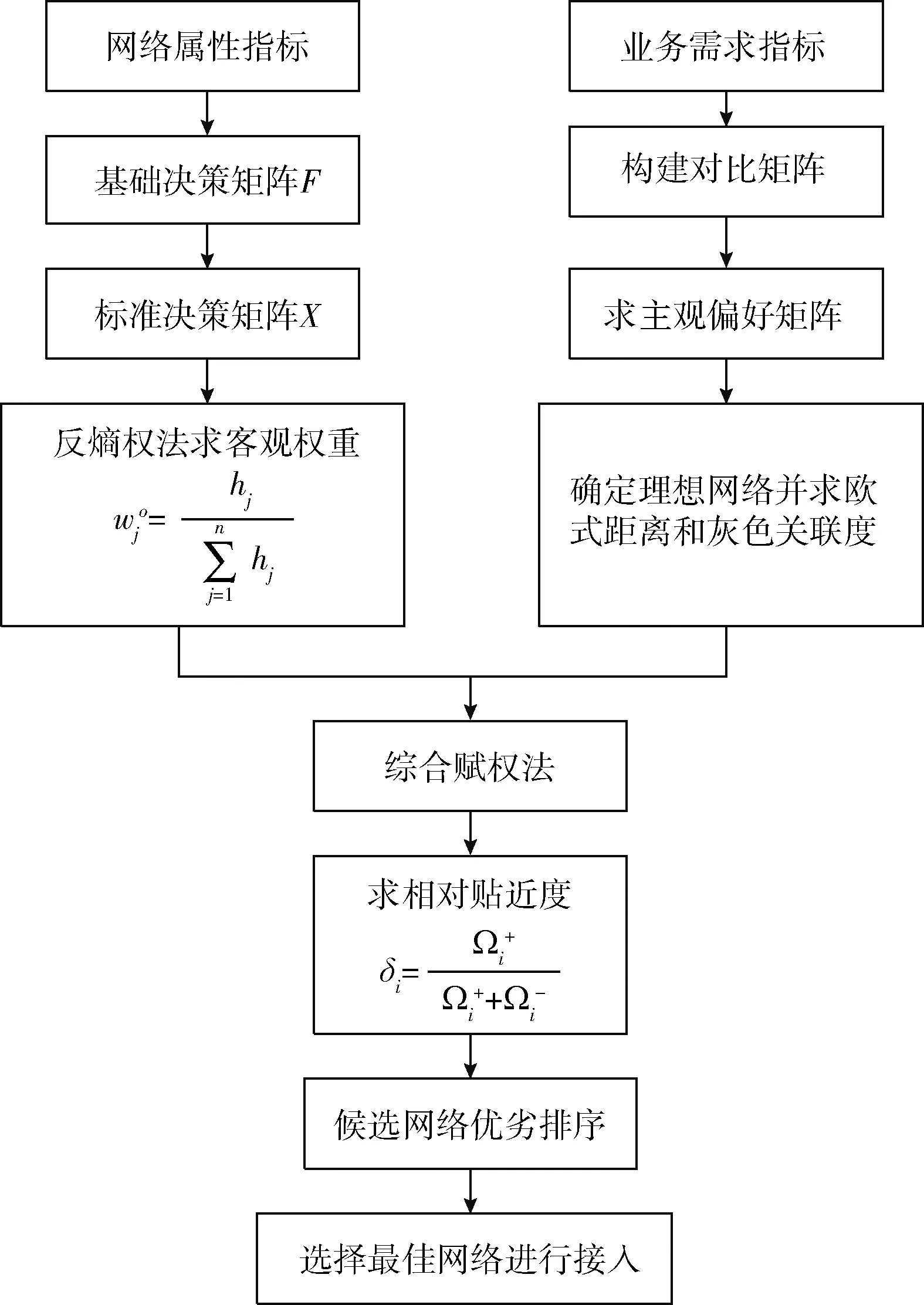
图2 智能配电异构无线网络接入选择算法流程
2.3 算法步骤
2.3.1 构建标准决策矩阵
(1)构建基础决策矩阵
假设在智能配电异构无线网络中,有m个无线网络对智能配电终端节点实现重叠覆盖,配电业务进行接入时需要考虑n个指标,从配电终端提取所需参数,构建如式(1)所示的可表征网络性能的基础决策矩阵F,fij表示第i个候选网络决策指标j的值
(1)
(2)构建标准决策矩阵
对基础决策矩阵F中的决策指标执行同向化和无量纲化处理,生成标准决策矩阵X:
1)决策指标同向化
将所参考的n个决策指标分为正向指标(即越大越好型)和负向指标(即越小越好型)两种。
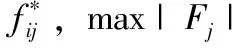
(2)
(3)
2)决策指标去量纲化
经过同向化处理后的各决策指标在属性性质、量纲、度量标准等方面仍然存较大的差异性,因此需采用式(4)对所得正向指标进行去量纲化处理,可得如式(5)所示的标准决策矩阵X
(4)
(5)
2.3.2 确定决策指标权重并构建加权标准化矩阵
(1)确定配电业务主观权重
根据不同类型配电业务的需求差异,采用层次分析法构建如图3所示的层次结构模型为各决策指标赋权。该架构的目标层为最佳接入网络,准则层包含抖动、带宽、丢包率、时延、及单位字节费用等决策因素,方案层包括了当前的所有候选网络。
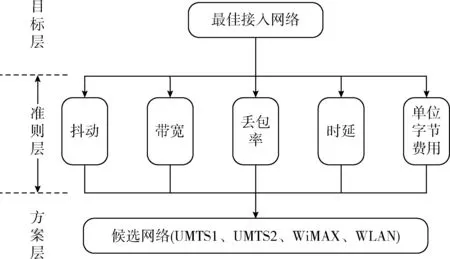
图3 异构网络接入选择层次结构模型
此处采用几何平均法[9]求取各决策因素的相对重要性即权值如式(6)所示
(6)
式中:bij——决策指标xi与决策指标xj之间的相对重要性级别。
(7)
(2)确定网络性能客观权重
信息反熵和信息熵具有相同的属性,均可用于度量系统无序程度[10,11]。由于熵权法不能根据指标差异合理分配权重,极端情况下会出现某些指标权重过小使其不具备参考价值,故而此处采用反熵权法求取候选网络性能指标的客观权重Wo,具体步骤如下:
1)以标准决策矩阵X为基础,计算各决策指标的比重,如式(8)
(8)
2)依据反熵的定义,确定各决策指标的反熵,如式(9)
(9)
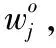
(10)
(3)计算指标组合权重
由于指标性质间存在差异,对应主客观权重所占比重也不同。分别用α和β表示主观权重和客观权重所占比重,结合矩估计理论,根据式(11)求取各决策指标的主客观权重系数αj和βj[12]
(11)
为综合考虑主客观因素,将所得业务需求的主观权重集Ws、网络性能的客观权重集Wo和主客观权重所占比重系数相结合,根据式(12)可求取主、客观权重综合之后的最优组合权重vj
(12)
(4)构建加权标准化矩阵
将计算所得最优组合权重vj与标准决策矩阵X相乘构建加权标准化加权矩阵Y如式(13)所示
(13)
2.3.3 确定理想网络并求解欧式距离和灰色关联度
(1)确定能够评价候选网络的正理想网络和负理想网络
由于决策指标经同向化处理均已转化为正向指标,故可用加权标准化决策矩阵Y中各指标的最大值构成正理想网络Y+如式(14),用各指标的最小值构成负理想网络Y-如式(15)
(14)
(15)
(2)求解候选网络到正理想网络和负理想网络之间的欧氏距离
假定第i个候选网络距离正理想网络的欧氏距离为D+,根据式(16)可得
(16)
假定第i个候选网络到负理想网络的欧氏距离为D-,根据式(17)可得
(17)
(3)求解候选网络与正理想网络和负理想网络间的灰色关联度
1)在加权标准化矩阵Y的基础上,根据式(18)求解第i个候选网络与正理想网络关于第j个决策指标的灰色关联系数,即
(18)
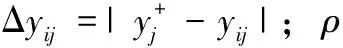
(19)
第i个候选网络与正理想网络之间的灰色关联度为
(20)
2)计算第i个候选网络与负理想网络关于第j个决策指标的灰色关联系数,如式(21)
(21)
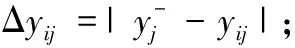
(22)
第i个候选网络与负理想网络的灰色关联度为
(23)
2.3.4 求解相对贴近度并对候选网络进行优劣排序
(1)利用式(24)对所求欧氏距离和灰色关联度实施规范化处理
(24)
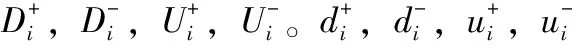
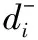
(25)
(26)

(3)相对贴近度体现了候选网络与正理想网络或负理想网络在变化趋势上的接近程度,用δi表示相对贴近度,则有
(27)
(4)按照所求相对贴近度δi的大小对候选网络进行优劣排序,δi越大,表示候选网络与正理想网络越贴近,候选网络质量越优,能较好地满足当前业务需求;反之,δi越小,表示候选网络与负理想网络越贴近,候选网络质量越差,不能较好满足当前业务需求。当确定出候选网络性能质量的优劣排序后,选取δi最大的候选网络为最合适的网络选择。
3 仿真与分析
为检验所提智能配电异构无线网络接入选择算法的性能优劣,使用MATLAB在图1所建模型中进行模拟仿真,假定该重叠覆盖区域中含有150个终端节点,获取网络性能参数,得到如表2所示的初始决策矩阵。在相同的仿真环境下,对4类配电通信业务同时执行本文算法和文献[13,14]中所提层次分析法和TOPSIS相结合的传统算法,将两种算法连续执行20次并取其平均值就网络排序异常率、单一业务情景、综合业务情景和网络总平均阻塞率下的情况进行仿真模拟对比。
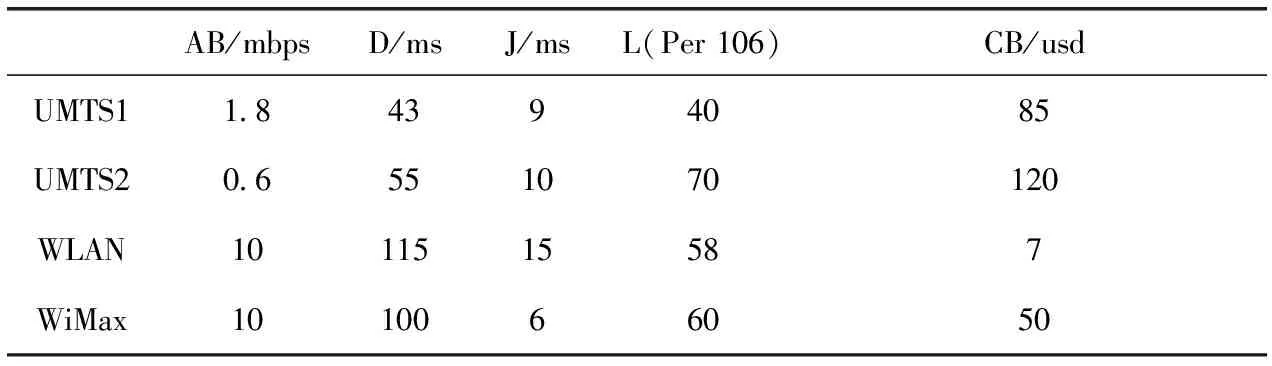
表2 候选网络的决策属性值
结合4类配电业务的需求,对网络带宽(AB)、网络时延(D)、网络抖动(J)、网络丢包率(L)和单位字节费用(CB)这5项指标之间进行成对比较,构造如表3所示的成对比较判断矩阵,利用层次分析法求得如图4所示的4类配电业务关于决策指标的权重分布关系。
3.1 逆序问题性能比较
图5是在4类配电业务下,采用本文算法和传统TOPSIS法时平均排序异常概率分布。

表3 4类配电业务需求间的成对比较判断矩阵
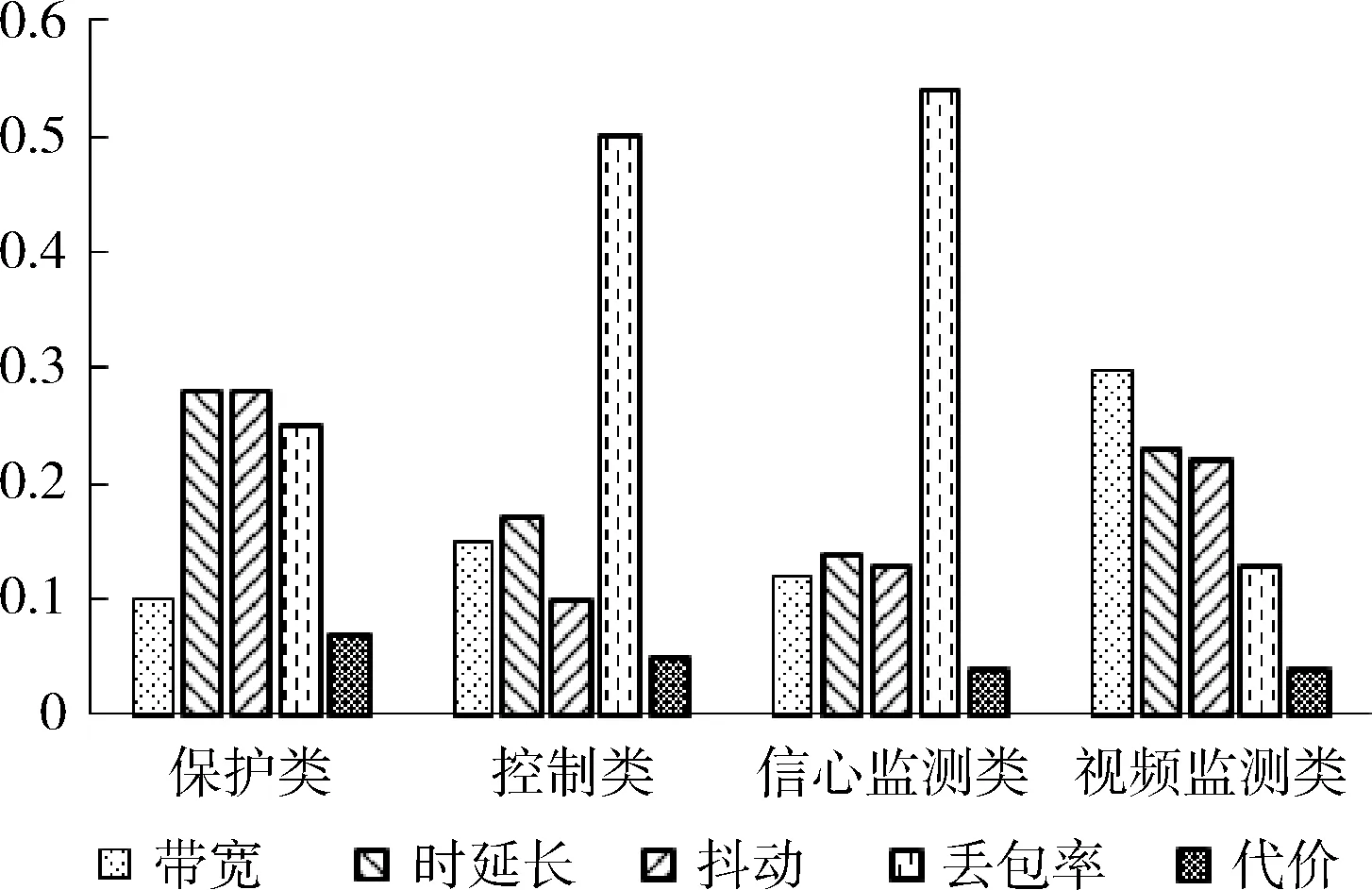
图4 4类配电业务需求偏好值
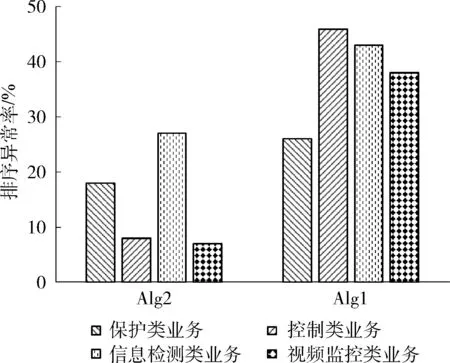
图5 4类配电业务下的平均异常排序率注:Alg1:传统TOPSIS法,Alg2:本文算法
从图5可知,在4种业务同时开展的情况下,本文算法的排序异常率均低于传统TOPSIS法。本文算法在构建标准决策矩阵前已采用了同向化处理过程,且能够将各方案与理想方案间的内部因素变化趋势和整体相似度相结合,通过将所求欧氏距离和灰色关联度相结合,求取更为确切的综合相对贴近度,保证了所选网络在距离负理想方案最远的同时又是最接近正理想方案,同时满足形状和位置两个不同性质的双重要求。最终可确定最终候选网络间的优劣排序,使得网络间的逆序现象得到改善。
3.2 单一业务情景下的终端负载分布
以终端节点执行同一类型业务为例,分别执行本文算法和传统TOPSIS算法使终端从可用候选网络中确定出能够满足当前业务需求的最合适网络并进行接入,图6为4类业务在两种方法下的终端负载分布结果。
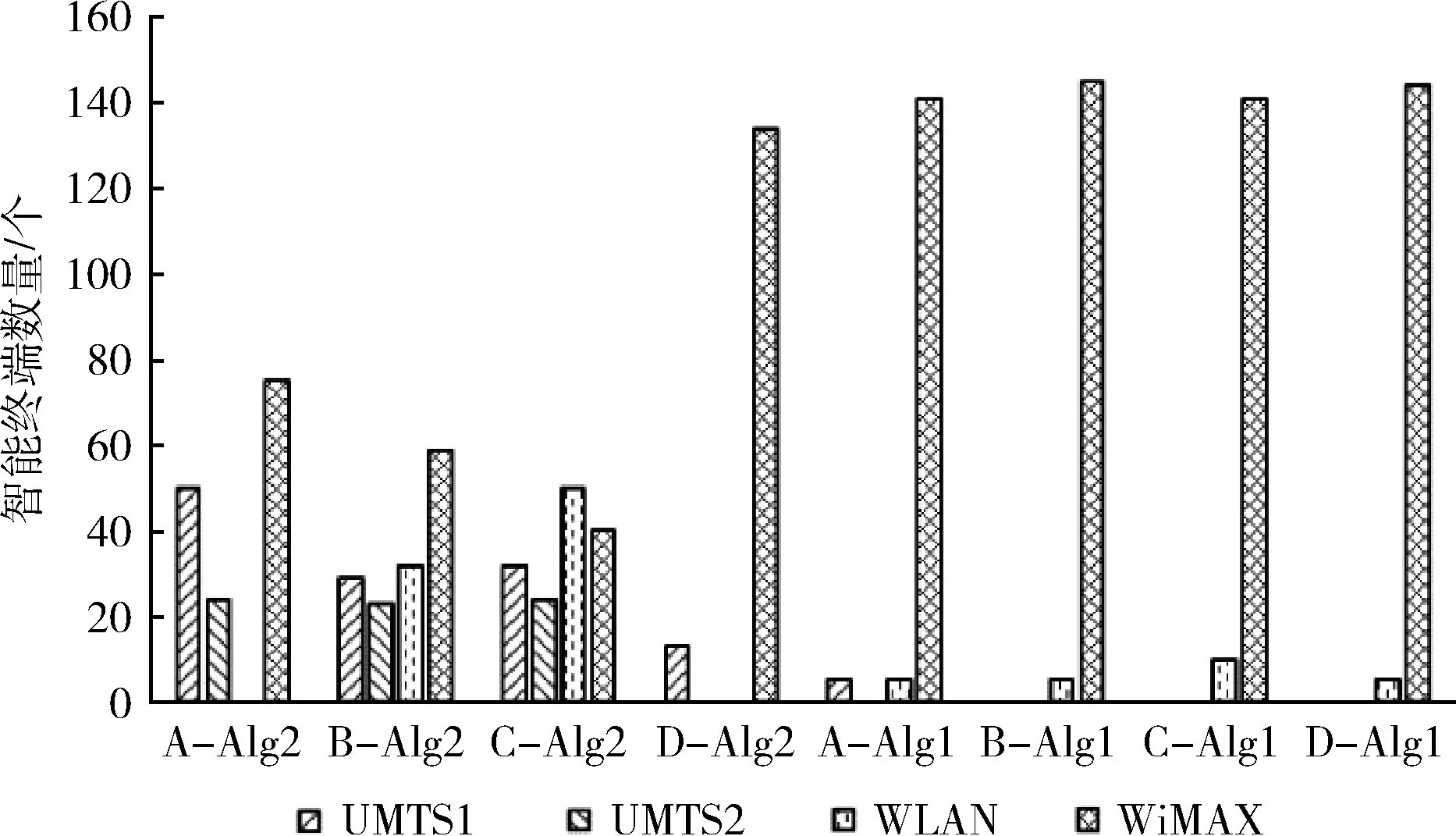
图6 单一业务场景下终端业务分布注:A:保护类业务,B:控制类业务,C:信息监测类业务,D:视频监控类业务;Alg1:传统TOPSIS法,Alg2:本文算法
由图6可知,当终端执行传统的TOPSIS网络选择算法时,4种业务有超过90%左右的终端会选择WiMAX网络进行业务接入,导致WiMAX网络拥塞程度加重,造成网络负载过重,进而会形成因终端业务请求不能被满足导致接入率降低、掉线率升高;同时也会使得UMTS1,UMTS2和WLAN网络资源不能得到充分利用。当终端采用本文所提所算法时,承载保护类、控制类、信息监测类3类业务的终端能够较均匀的分布于候选网络中,使网络处于较均衡状态。当业务为视频监控类业务时WiMAX网络才会出现负载过重的现象,造成网络拥塞。综上所述,在单一业务情境下,较传统TOPSIS算法相比,本文所提算法的负载均衡效果较好。
3.3 综合业务情景下的网络选择概率
在4种业务随机产生的情况下,终端结合网络性能和业务需求执行本文所提智能配电异构无线网络接入选择算法,选出合适的网络进行接入,4种网络接入选择概率如图7所示。假定初始时刻4种候选网络皆处于空载状态,终端不论执行哪种类型业务,在满足业务需求的前提下,终端均会优先选择性价比较高的网络。随着请求入网的终端业务数不断增加,网络的负载量、部分性能也随之改变,为保证终端业务能够正常运行,且能够较均匀地分布于各网络中,终端则会有针对性地选择网络,最终呈现出4种网络被选概率趋于一致的现象。
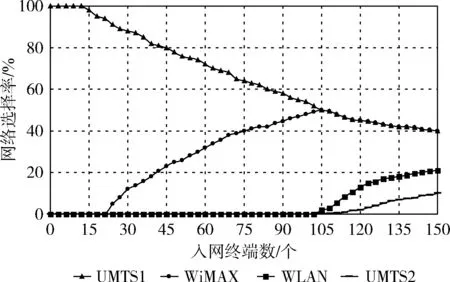
图7 综合业务下网络接入选择率
3.4 网络的总平均阻塞率比较
图8为本文所提算法、多接入选择算法(MLB)和传统TOPSIS算法关于网络总平均阻塞率的仿真对比结果。随着终端业务数的增加,3种算法在网络总平均阻塞率方面的差异性逐渐显现出来,采用本文算法的网络总平均阻塞率一直低于MLB法和传统TOPSIS法的网络总平均阻塞率。MLB法和传统TOPSIS法在实现业务接入选择的过程中仅考虑了不同类型配电业务的个性化需求和网络性能,使最终的决策结果比较片面;本文所提算法除考虑以上因素外,重点考虑了业务的重要性程度,因为业务接入时重要程度高的保护类和控制类业务优先接入网络,且重要程度高的业务占用的网络资源较少。因此,采用本算法能够实现对候选网络的综合评价,使得网络中的负载分布更为均匀,从而降低了整个网络的阻塞率。
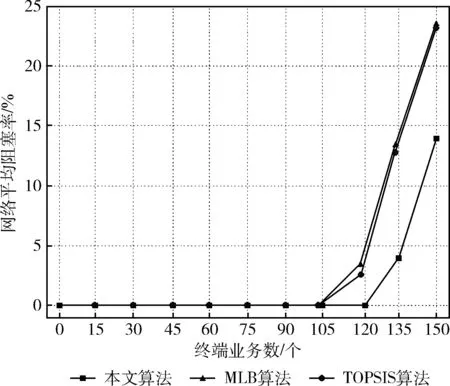
图8 网络总平均阻塞率对比
4 结束语
针对智能配电异构无线网络接入选择问题,提出了一种基于相对贴近度的智能配电异构无线网络接入选择算法。通过构建灰色理想逼近模型求解相对贴近度,以此为依据对候选网络进行优劣排序选出最适合业务传输的网络。与已有的网络选择算法相比,该方法能反映出候选网络内部各因素变化趋势与理想方案之间的区别,实现对各候选网络进行整体评判,是一种更有效的网络选择方法。仿真结果表明,该算法降低了网络平均排序异常率,在满足各类配电业务服务质量需求的同时,将终端较均匀的分布于各网络中,有效减缓拥塞的形成,改善了因负载分布不均造成的网络资源浪费的现象,提高了配电业务的传输可靠性。
下一步,本文将针对该接入选择算法的负载均衡,调度优化进行进一步的研究。

