面向数据中心的多级交换网络性能分析与优化
高 雅,潘伟涛,郑 凌
(1.无锡职业技术学院 物联网技术学院,江苏 无锡 214121;2.西安电子科技大学 综合业务网国家重点实验室,陕西 西安 710071)
0 引 言
Clos结构多级交换网络由于其模块化、可扩展的特点,成为数据中心交换网络的重要解决方案[1]。在Clos交换网络的中间级设置缓存,如中间级和输出级有缓存交换(space-memory-memory,SMM)或各级有缓存交换(memory-memory-memory,MMM),能够有效避免各级无缓存交换或输入输出级有缓存交换[2]中复杂的匹配调度和缓存加速问题,具有更加灵活的可扩展性。然而,中间级缓存的存在会引起输出端口信元乱序,可通过复杂的背压反馈[3]、逐帧调度[4,5]、模拟输出排队交换[6,7]等方法控制乱序信元产生,或者在输出端口进行乱序重排[8]。从已有文献的研究成果可看出,增加各级模块的缓存大小能够提高吞吐率,但同时会加剧乱序程度。各级模块的缓存大小具体如何影响交换网络的吞吐率和时延性能,最大重排时延以及重排缓存的规模受哪些参数影响,给定重排缓存规模时各级模块内的缓存大小如何设置以获得最优性能等问题仍未解决。本文对以SMM结构为代表的中间级有缓存的Clos交换网络(central-stage buffered switch,CBS)的性能进行了研究。通过理论分析和仿真验证的方法研究了中间级和输出级缓存规模对CBS交换吞吐率和时延性能的影响,给出了定性和定量的分析。同时,推导了最大重排时延以及重排所需缓存大小,并比较了不同缓存配置下的平均重排缓存时延性能,得到有限条件约束下性能最优时的配置参数。
1 交换网络模型与参数
图1所示为中间级有缓存的Clos交换网络。第一级有k个输入模块(input module,IM),每个输入模块为n×m的无缓存Crossbar交换单元,其中k=N/n,N为交换网络端口数。第二级为m个中间级模块(central module,CM),每个CM为k×k的交叉点有缓存Crossbar交换(crosspoint-queued,CQ),来自IM(i)到达CM(r)目的模块为OM(j)的信元入队XBC(r,i,j)。第三级为k个输出级模块(output module,OM),每个OM为m×n的CQ交换,经由CM(r)到达OM(j)需去往第h+1个输出端口的信元入队XBO(j,r,h)。CM和OM中交叉点缓存规模分别为KC和KO。其中0≤i,j≤k-1,0≤r≤m-1,0≤h≤n-1。通常将上述Clos网络记为C(m,n,k)。为讨论方便,取m=n=MO,同时令k=MC。
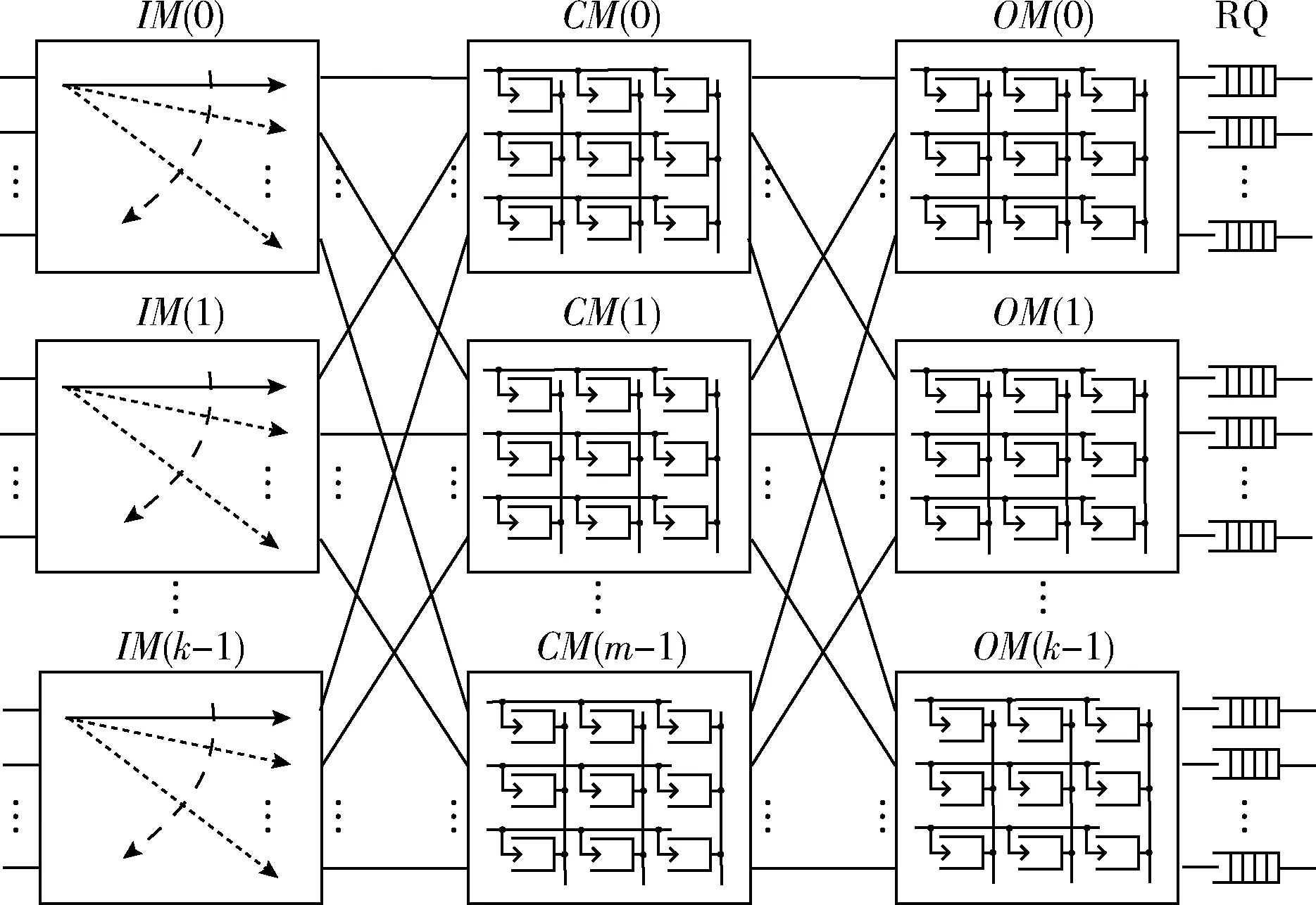
图1 CBS交换结构
变长分组被切割成定长信元,传输一个定长信元所需时间称为一个时隙。CBS交换网络的输入级采用固定的周期性轮转配置,每n个时隙轮转一次;中间级和输出级采用CQ交换单元,各模块输出端口采用随机调度或轮询调度算法。信元在离开输出级模块后进入重排缓存队列(re-sequencing queue,RQ)。
2 理论分析
2.1 吞吐率性能的统计平均值
由于CBS交换的后两级模块均为CQ结构,首先基于马尔科夫链模型计算CQ交换的吞吐率性能的统计平均值,然后根据获得的结果进一步计算CBS交换的吞吐率性能。
令M为CQ交换的端口数,B为一个交叉点缓存可容纳的信元数。每个时隙的开始为信元到达阶段,随后为调度离开阶段。由输入端口g到达需去往输出端口h的信元,缓存在交叉点Qg,h;若缓存已满,则该信元被丢弃。在一列交叉点缓存中,即{Qg,h|0≤g≤M-1}, 输出端口h随机选择一个非空缓存进行调度。定义d(t)为一个交叉点缓存被调度的概率。在Bernoulli i.i.d。均匀到达业务下建立CQ交换模型,每个时隙每个输入端口有信元到达的概率为ρ,每个交叉点缓存有信元到达的概率为ρ/M。
令πj(t)表示在第t个时隙结束时交叉点缓存Qg,h包含j个信元的稳态概率,如图2所示。由于每个交叉点缓存有B+1个状态,将这B+1个稳态概率表示成列向量S(t),即S(t)=(π0(t),π1(t),…,πB(t))T。 假设被观察缓存的状态只依赖于其前一个时隙的状态。

图2 基于单个交叉点缓存状态的马尔科夫链模型
状态转移矩阵P是 (B+1)×(B+1) 非负实数方阵,其中的元素pi,j表示交叉点缓存从前一个状态πi(t-1)转移到状态πj(t)的概率,0≤pi,j≤1,0≤i,j≤B。接下来,可通过迭代计算的方式获得稳态概率的值
(1)
即
S(t)=PS(t-1)
(2)
首先初始缓存为空,即t=0时
π0(0)=1
(3)
πj(0)=0,1≤j≤B
(4)
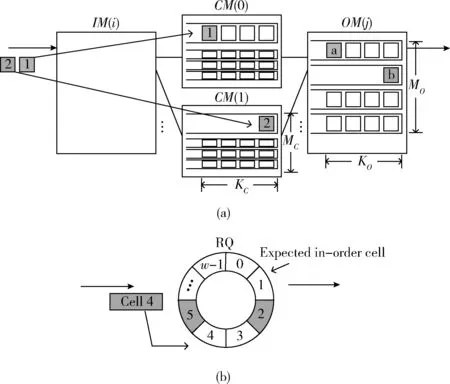
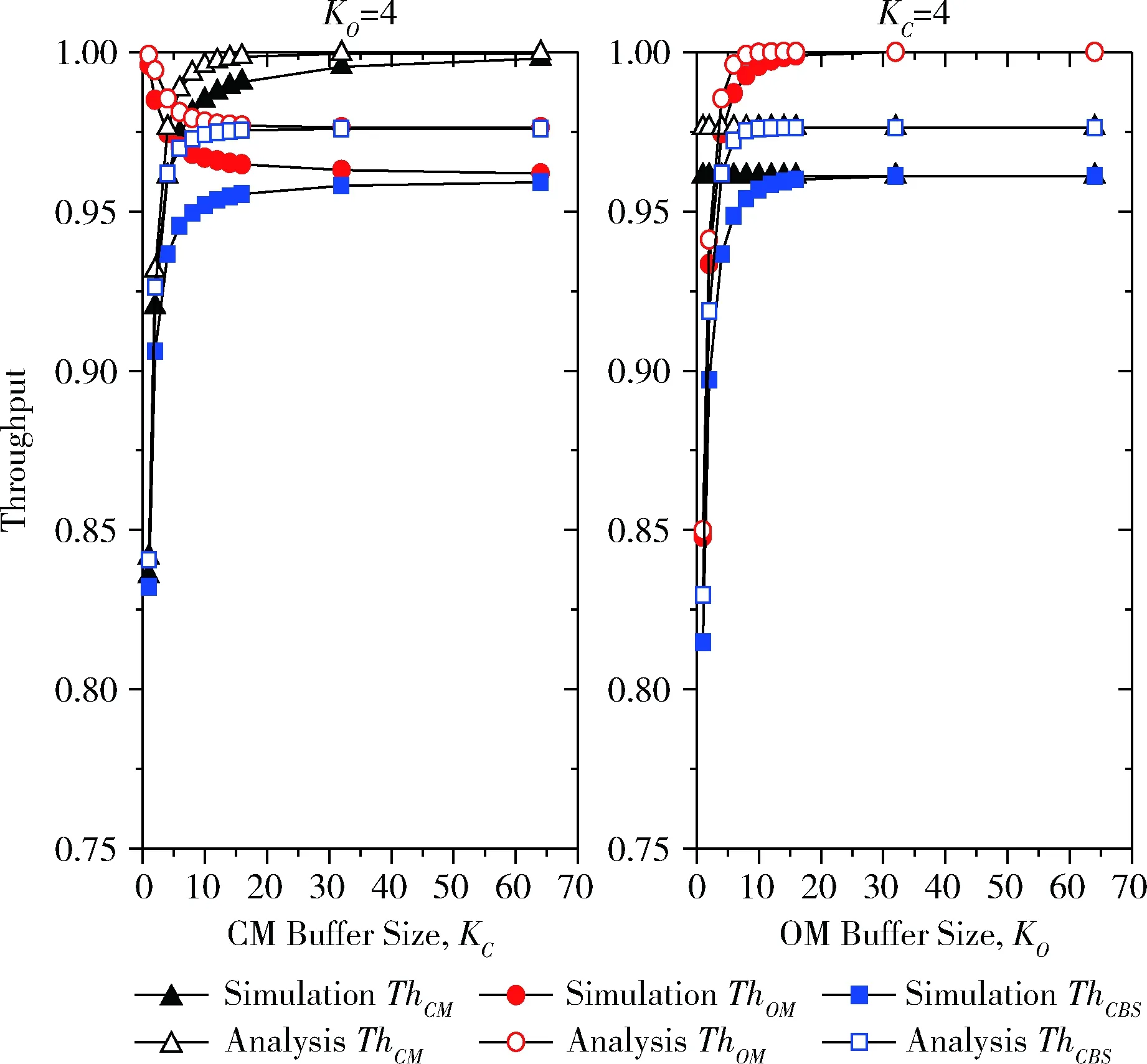
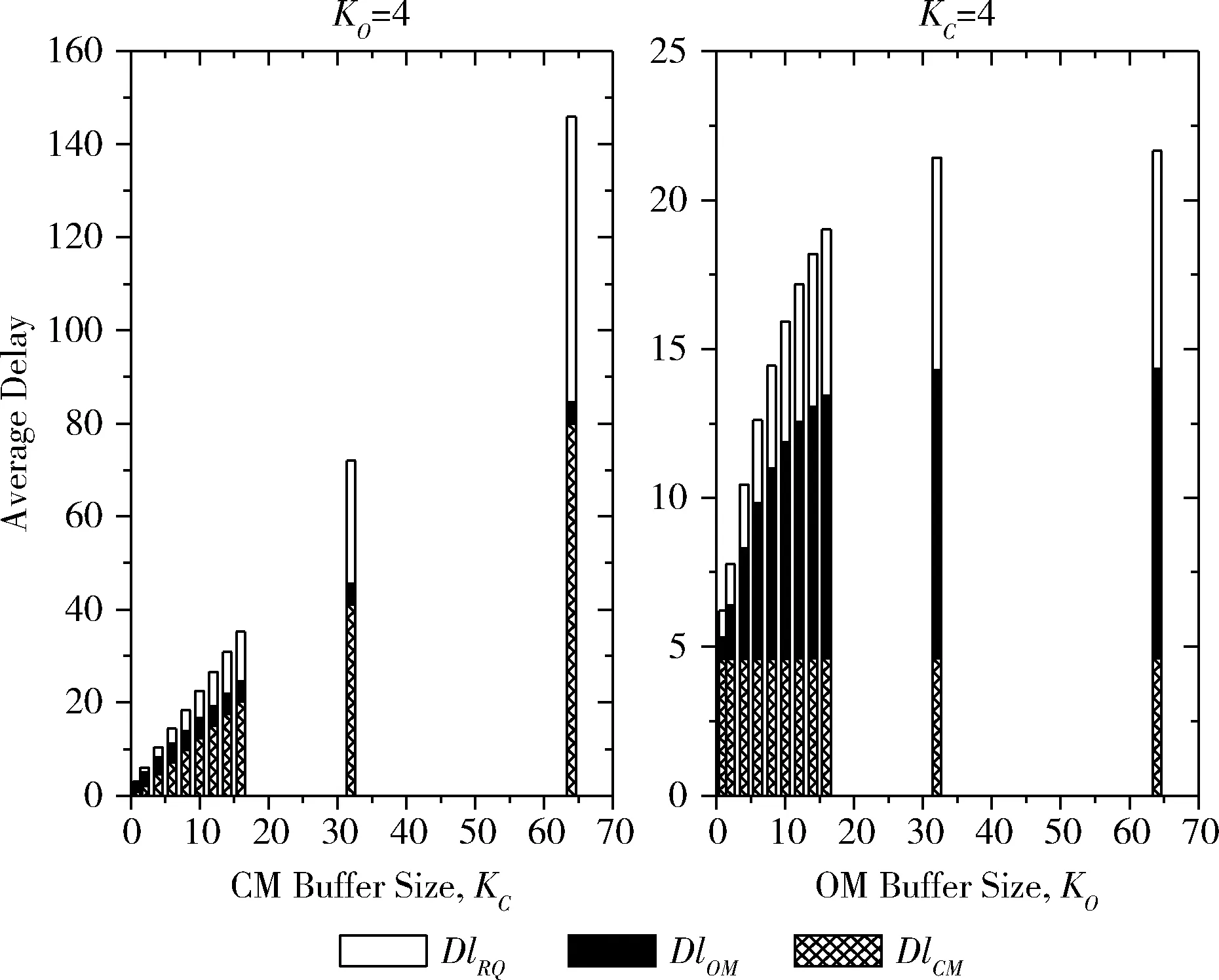
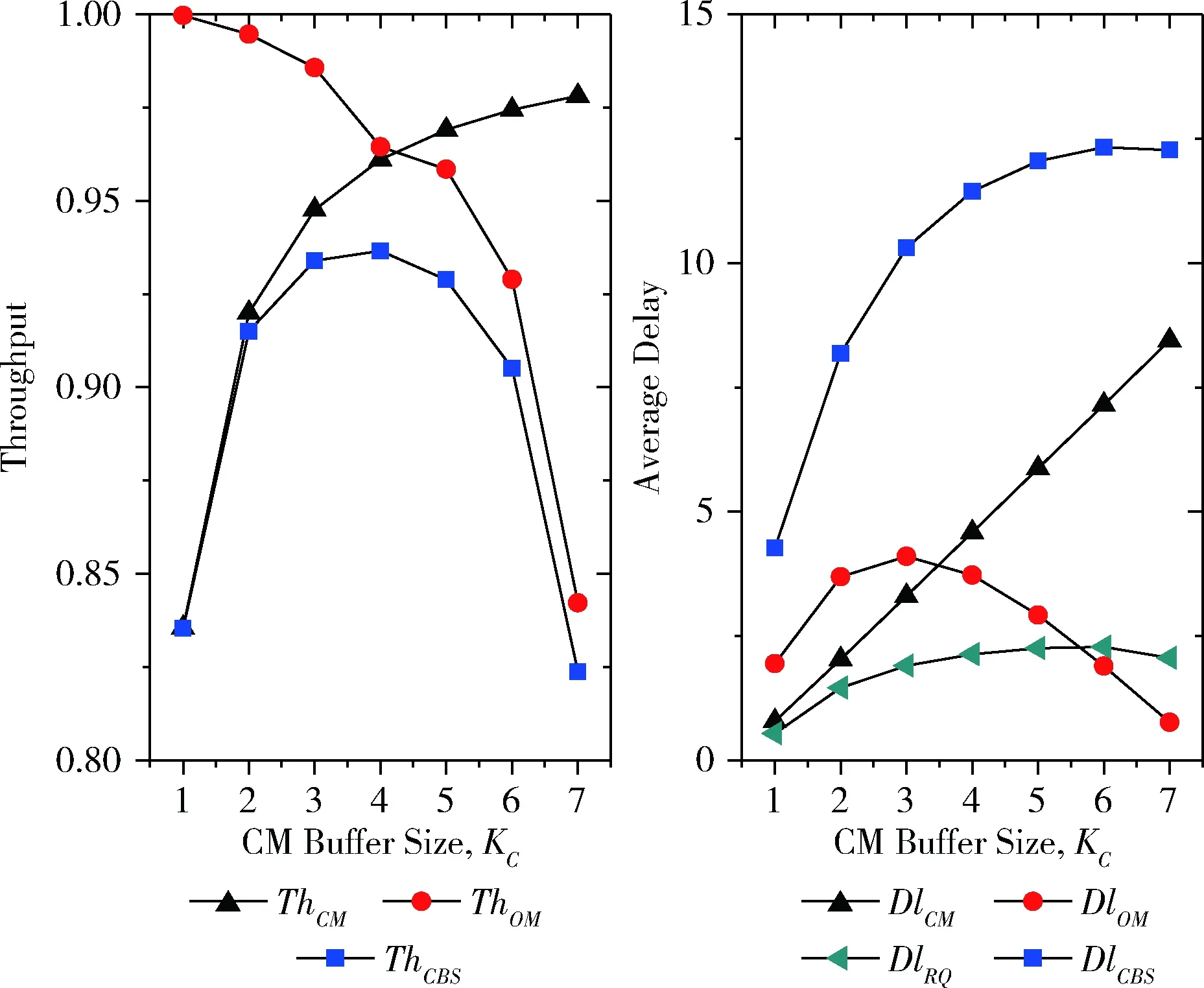
由于一个交叉点每个时隙最多到达一个信元,最多离开一个信元,因此对于j>i+1或者j 当i=0时 (5) (6) 如p0,0反映了交叉点缓存状态变化的两种情况,分别是到达一个信元且被调度离开,以及没有信元到达。p0,1则表示有信元到达,且未被调度的概率。 当1≤i≤B-1时 (7) (8) (9) 当i=B时 pB,B-1=d(t) (10) pB,B=1-d(t) (11) 为简化离开状态的模型,假设同一个输出链路的交叉点缓存具有相同的状态分布。非空交叉点缓存被调度的概率d(t)与同一个输出线上其它缓存的状态相关。若除外还有i-1个非空缓存,则该缓存能够发送队首信元的概率为1/i。而一个缓存在调度期间为空的概率为π0(t-1)(1-ρ/M)。 基于上述描述以及全概率公式[9],离开概率表示为 (12) 由于输入业务的均匀性和交换网络的对称性,可通过考察同一输出端口的一列交叉点缓存的性能来表示整个交换网络的性能[9,10]。当同一个输出线的所有缓存为空时,该输出端口不会调度信元。因此归一化的相对吞吐率TCQ可通过下式计算出 (13) 当t趋于无限,将获得吞吐率性能的稳定结果。也就是说最终TCQ是CQ交换端口数M,交叉点缓存规模B和输入负载ρ的函数,表示为TCQ=f(M,B,ρ)。 CBS交换的后两级交换单元,可以分别看作两个CQ交换,其中后一个CQ交换的输入为前一个CQ交换的输出负载。这里假设进入输出级模块的均匀业务是符合Bernoulli i.i.d.过程的。因此CBS交换的相对吞吐率TCBS表示为 TCBS=TCM·TOM= (14) 乱序程度可通过最大重排缓存时延和平均重排缓存时延这两个指标来衡量。只有当各路径上的缓存为有限规模,且信元等待调度的时延存在上限,才能获得重排缓存时延的上限值。 定义来自IM(i)的第g+1个输入端口需要去往OM(j) 的第h+1个输出端口的一系列信元为流(i,g,j,h)。CQ交换的各输出端口采用轮询调度算法。图3(a)给出了与流(i,g,j,h)相关的多条路径上的信元缓存及调度情况。同一个流的连续信元在多条路径上经历时延不一致会产生乱序。 图3 信元乱序及重排缓存 在CBS交换中,假设信元最快在1个时隙内经过输入级模块、中间级模块和输出级模块,以及重排缓存模块,进入输出链路。如图中信元2,在由输入级模块轮转到CM(1) 后紧接着被调度去往输出级模块,并在输出级模块获得同样的待遇。由于早于信元2的信元1还未到达输出端口,因此信元2只能在重排缓存模块中等待。而信元1进入中间级后,需要至多等待MCKC个时隙才能被调度,进入输出级模块后,同样需要等待MOKO个时隙。此时信元2已在重排队列中等待MCKC+MOKO-1个时隙。也就是说最差情况下重排时延为MCKC+MOKO个时隙。 CBS交换的输出端口设置有逐流重排缓存,每个重排缓存由一个可容纳w个信元的圆形队列实现[11]。重排缓存维护一个指针,用于记录下一个期待接收的按序信元的序列号。具体工作流程如下: (1)新到达的信元将按照序列号(sequence number,SN)取模的方式(即:SNmodw)被安置到相应位置,如图3(b)中信元4被安排在缓存4号位。 (2)若新到达的信元恰好是指针指向位置的被期待信元,则该信元将被调度发往输出线卡,如图中指针指向位置需要等待信元1,而信元2已经缓存在重排缓存模块中。同时按序指针更新至下一位。 (3)若指针指向位置已有信元到达,表明该信元也是按序的,将随着按序指针的更新逐个发送出去。 (4)最终,按序指针将指向被期待的空信元位置。 由于信元除了要等待序列号小于自己的信元到达重排缓存,还需要等待被逐个调度离开重排缓存。因此重排缓存的每个队列需要容纳至少2MCKC+2MOKO个信元才能保证没有信元在等待重排和调度时被丢弃,即取ω=2MCKC+2MOKO。 由于每个输出端口需要维护N个重排队列,因此对于整个多级交换网络而言,需要的重排缓存规模为2N2(MCKC+MOKO)。 基于OPNET网络仿真系统,分别仿真了不同中间级模块和输出级模块缓存大小、不同输入负载ρ、不同交换规模的CBS交换网络,统计了业务在不同模块中的时延和吞吐率性能,如中间级模块、输出级模块和重排缓存模块,以及CBS交换的整体性能,并与理论分析值进行了比较。到达业务为Bernoulli i.i.d.的均匀业务,输入和输出都是可允许业务。仿真时长为200 000个时隙。 图4比较了ρ=1时C(4,4,4)的CBS交换吞吐率性能的仿真值和理论值。中间级和输出级模块的归一化相对吞吐率,理论值均略高于仿真值,总吞吐率ThCBS累积了这部分误差,最大误差约为2.70%(发生在KC=4,KO=4时),但总体趋势一致。CBS交换的吞吐率ThCBS不会超过中间级和输出级模块吞吐率的最低值。单独提高中间级和输出级模块的缓存大小,ThCBS提高。对于给定的KO,ThOM随着KC的增加而降低。这是因为中间级模块可缓存的信元越多,吞吐率性能提高,则进入输出级模块的业务量越大,丢包率提高。 图4 不同缓存规模时吞吐率性能的仿真值与理论值 如图5所示,信元在中间级模块、输出级模块和重排缓存模块中经历的时延被分别统计,共同组成信元的端到端时延。随着KC的增大,信元在中间级模块中的时延、重排时延增加,并造成端到端时延呈线性增加。相比而言,输出级模块中缓存规模的增加,不会对中间级模块中的时延产生影响,且输出级模块和重排缓存模块中的时延增幅远低于前一种情况。由此可看出,缓存在中间级和输出级模块中不同的数量会影响到平均重排时延的大小,并影响到端到端的时延。在最大重排缓存时延MCKC+MOKO相等的条件下,KO较大的平均端到端时延较小。如图5所示,KC=64,KO=4时的端到端时延要远高于KC=4,KO=64时的端到端时延。 图5 各级模块的缓存大小对时延性能的影响 为比较不同交换规模对吞吐率和时延性能的影响,分别仿真了C(4,4,4)和C(8,8,8)的CBS交换在不同缓存规模时吞吐率和时延性能随输入负载变化的情况。时延和吞吐率性能随着交换规模的增加均有所提高。从图6可看出对于KC=1且KO=1的CBS交换网络,增加输出级模块中的缓存数目(如:KC=1,KO=4)比增加中间级模块中的缓存(如:KC=4,KO=1)能更有效地提高吞吐率,且端到端时延增量更小。 图6 不同交换规模和输入负载对性能的影响 为考察在给定重排缓存规模时,中间级和输出级模块内的缓存大小如何设置,仿真了在KC+KO=8限制下不同KC和KO组合的CBS交换网络,其中N=16,ρ=1。如图7 所示,从获得的吞吐率性能看,当KC和KO值相近时,可以获得吞吐率最高值。而端到端时延则几乎是递增状态。中间级模块中的时延随着KC的增加而线性递增,而输出级模块中的时延首先随着到达输出级模块的信元增加呈上升趋势,最后,由于KO减少,时延下降。 图7 给定重排缓存规模时缓存大小对性能的影响 各级模块的缓存规模对时延和吞吐率性能的作用并非简单的线性关系,缓存的大小和分布,对交换网络的性能具有重要影响。本文基于理论分析和仿真验证的方式研究了多级交换网络各参数对性能的影响。得出结论如下: (1)各级模块中交叉点缓存规模最小的模块其吞吐率决定了交换网络吞吐率的上限。 (2)增加各级缓存规模有利于提高吞吐率,但同时会增加端到端时延,以及所需的重排缓存规模;其中增加输出级模块的缓存规模要优于增加中间级模块的缓存规模。 (3)中间级和输出级模块的端口数以及交叉点缓存的大小共同决定了所需重排缓存的规模;对于重排缓存规模已知的情况,合理设置中间级和输出级模块的缓存大小可以达到吞吐率的最优值。 本文的研究为设计与实现面向数据中心应用的多级交换网络提供了重要的理论依据。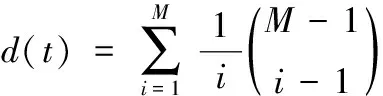
f(MC,KC,ρ)·f(MO,KO,ρf(MC,KC,ρ))2.2 重排缓存规模
3 仿真验证
3.1 缓存分布对性能的影响
3.2 交换规模和业务负载对性能的影响

3.3 已知重排缓存规模时的优化设置
4 结束语

