对MIBS分组密码的差分故障攻击
王永娟,张诗怡,王 涛,高 杨
(信息工程大学网络空间安全学院 郑州 450000)
随着物联网技术的蓬勃发展,近年来,适用于资源受限环境的轻量级密码算法受到研究者青睐,MIBS算法[1]是2009年提出的一个基于Feistel结构的轻量级分组密码算法,分组长度64 bit,支持64 bit和80 bit密钥长度,记为MIBS-64和MIBS-80,迭代轮数为32轮。MIBS算法所需硬件成本仅为1 396 GE和1 530 GE,适用于微型计算设备。目前,对MIBS的分析方法主要有差分分析、不可能差分分析、线性分析、零相关分析和积分分析等。文献[2]利用MILP(mixed-integer linear programming)技术研究了MIBS抵抗差分攻击的活跃S-盒下界,结果表明18轮的迭代足以抵抗单密钥的差分分析,39轮对于相关密钥差分分析是安全的;文献[3]提出了一种改进的差分故障分析方法,通过在第2~4轮的密钥中导入半字节故障,可将主密钥搜索空间降至22;文献[4]利用轮密钥间的制约关系与查表操作对13轮的MIBS-80算法进行了较为高效的不可能差分分析,总共需要个选择明文,次13轮加密与bit的存储量;文献[5]利用个明密文对对19轮的MIBS-80实施了时间复杂度为的线性分析;而文献[6]则通过构造一个9轮的相关密钥不变偏差线性分析区分器,给出了对13轮的MIBS-80的线性分析算法,该算法可在的时间复杂度与的数据复杂度的条件下恢复部分轮子密钥信息;文献[7]研究了MIBS-80抵抗零相关线性分析的能力,结合MIBS-80算法轮函数嵌套SP的Feistel结构特点,给出了8轮零相关线性逼近,并对12轮MIBS-80进行零相关线性分析;文献[8]则对13轮的MIBS-80进行了多维零相关分析,需要约个明文和次加密,此外还对11轮的MIBS-80开展了积分攻击,需要约个明文和 259.8次加密。
差分故障攻击是将差分分析和故障攻击相结合提出的一种基于硬件的密码攻击技术。攻击原理是在密码算法加密过程某一轮注入故障,制造明文差分,利用得到的故障密文和故障动作,结合差分方程得到轮密钥可能值,通过多次注入故障可以快速缩小密钥空间,实现密钥破解。差分故障攻击将侧信道攻击和传统分析思想相结合,对基于硬件实现的轻量级密码算法攻击效果显著,差分故障攻击对SMS4[9]、PRESENT[10]、LED[11]、Piccolo[[12]、Keeloq[13]、Trivium[14]等轻量级密码算法具有较好的攻击结果。
故障攻击模型由故障时机、故障位置、故障动作和故障效果四方面构成,通常故障注入轮数越高,攻击效率越高。本文针对MIBS算法,提出改进差分故障攻击,通过建立输入差分、输出差分、可能输入值之间的三次元关系,只需在最后一轮半字节位置注入两次故障,即可确定最后一轮白话密钥,继而进行密钥恢复。攻击效率和成功率较标准差分故障攻击结果均有所提高。
1 MIBS分组密码算法
MIBS算法是一种Feistel结构的轻量级分组密码算法,采用Feistel结构,MIBS密码的分组长度为64 bit,支持64 bit和80 bit的密钥长度,分别记为MIBS-64和MIBS-80,迭代轮数为32轮。MIBS中所有迭代操作都是基于半字节的,即一个字有4 bit。MIBS的轮函数F是SPN结构的,包括异或子密钥,S盒(4×4)层和一个线性层P(分枝数为5),此处线性层是设计文档中线性混淆和字节置换的复合。一轮MIBS及轮函数如图1、图2及表1所示。

图1 MIBS算法结构图
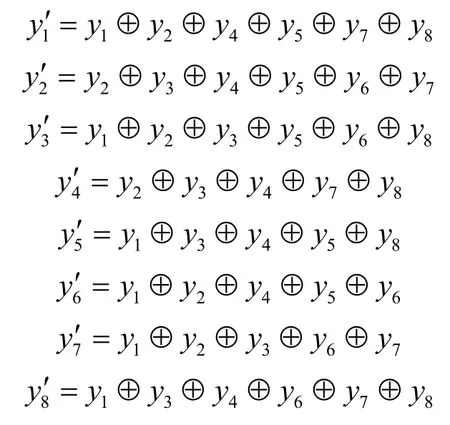

表1 MIBS算法轮函数
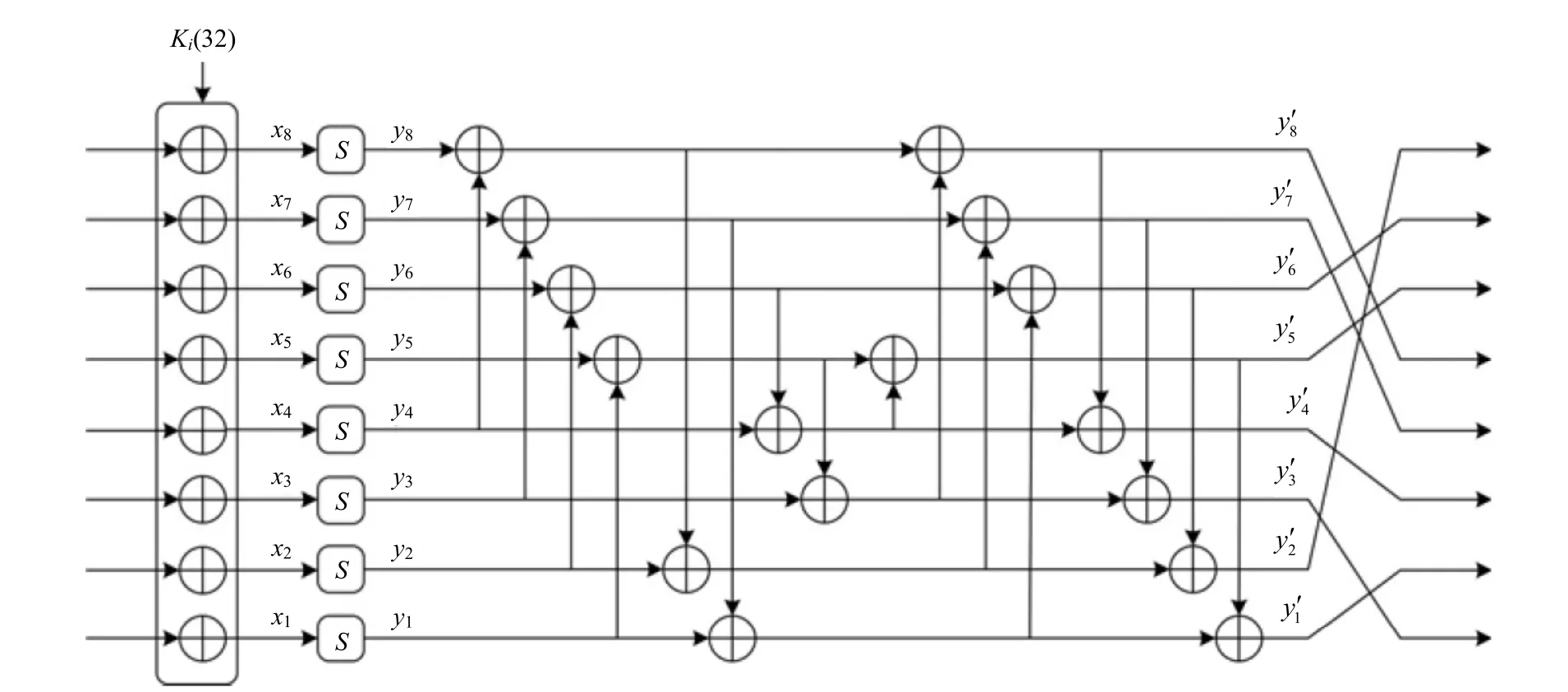
图2 MIBS算法的轮函数
由于密钥长度不同,MIBS-64和MIBS-80的密钥扩展方案略有不同,关于MIBS算法的详细加解密过程参见文献[1],本文不再赘述。
2 对MIBS算法的改进差分故障攻击
MIBS的差分S盒如表2所示。差分S盒体现S盒的差分分布全局特性,但对具体参数未有直观刻画。
目前分组密码算法普遍采用查找S盒来提高算法非线性度,但正是S盒的差分特性,导致其面临严重的故障攻击威胁。假设S盒输入值a未知,若在分组密码查表时导入随机故障值f,得到故障差分(密文差分)f′,则a,f,f′三者之间满足差分关系:
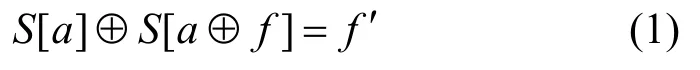
通过分析可以获得最后一轮S盒的输入值a,主要思路是通过故障分析降低f的搜索空间,代入式(1)恢复a和S[a]。输入值a与扩张密钥紧密相关,结合密文可以获取相关扩展密钥,再根据需要多次注入故障或者进行迭代分析直至获取主密钥。
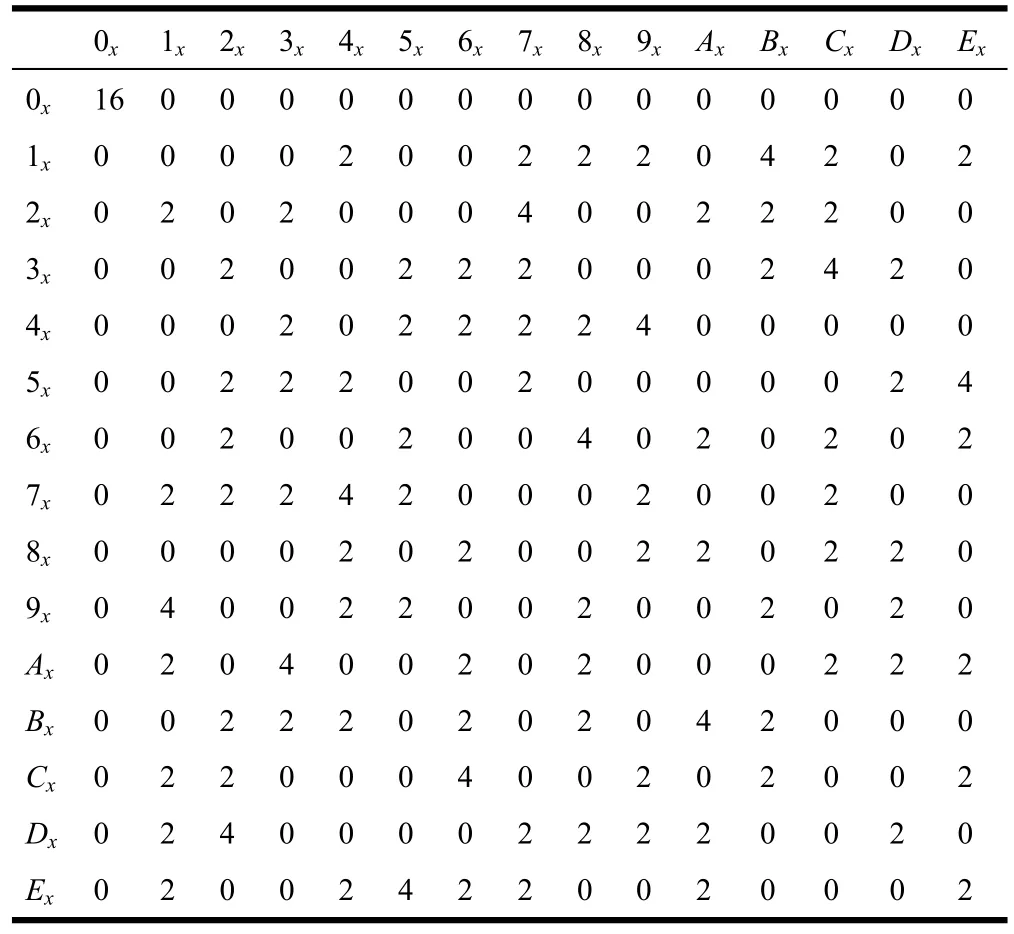
表2 MIBS差分S盒
本文在文献[10]基础上,分析分组密码算法S盒的差分传播特性,发现当S盒(n×n)输入差分f一定的情况下,对于每一个可能的输出差分f′,其对应的输入a可看成一个集合记为:
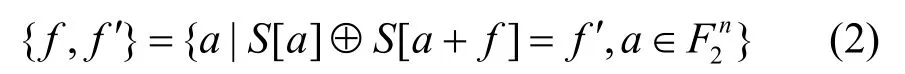
由式(2)易知,{f,f′}有如下性质:
性质 1 对分组密码算法S盒注入故障值f,对于不同的输出差分f1′f2′, ,对应输入值可能不交,即
性质 2 在输入a一定的情况下,对于两个特定不同的输入差分f1,f2,一定存在f1′f2′, ,使得
证明:令S是一个(n×n)的S盒,对S盒注入故障对应的故障差分空间为由S盒差分不均匀性可知F′是输入空间的一个真子空间,记则由定义和性质1可知的一个分割,满足
故对任意的输入值a,存在唯一一个集合使得不失一般性,记同理,对于故障值f2,存在唯一的集合满足从而有

表3 输入差分、输出差分、可能输入值对应关系
由MIBS算法的差分S盒可知,在理想情况下,只需在算法最后一轮注入两次不同故障,即可快速获得S盒输入a,从而高效准确地恢复出轮密钥,最后通过密钥扩展算法恢复主密钥。将此方法扩展到不同SP结构分组密码算法和部分Feistel结构的轻量级分组密码算法,均取得了良好的攻击效果。

图3 改进的差分故障攻击流程
3 攻击流程及数据分析
本节选取明文:01 23 45 67 89 ab cd ef,密钥:01 23 45 67 89 ab cd ef。
1)首先进行一次正确加密,得密文:a7 00 60 37 bf 97 81 07。
2)在最后一轮L31引入差分故障11 11 11 11,得到故障密文:4e 7d 29 e9 ae 86 90 16。将故障密文同正确密文异或得到:e9 7d 49 de 11 11 11 11。
3)将密文差分e9 7d 49 de通过逆P置换、逆列混淆后得到S盒的输出差分:e4 9e 49 79。
4)改变故障值为aa aa aa aa,得到另一组故障密文:a9 e8 03 b7 15 3d 2b ad。相应的可以得到差分密文:0e e8 63 80 aa aa aa aa。将左半部分密文差分 0e e8 63 80通过逆P置换、逆列混淆后得到S盒的另一组输出差分:d6 3d 63 33。
5)结合表确定出S盒未加故障时的输入:每一个未知的输入候选值均只有一个交集,这样就唯一确定出S盒的输入为:9d a9 da 5a。
6)将S盒输入:9d a9 da 5a与密文右半部分:bf 97 81 07异或得到最后一轮轮密钥k31:22 3e 5b 5d。从而得到31轮加密后的输出:bf 97 81 07 78 29 07 aa。
利用31轮加密后输出值,在第30轮注入两次故障,可以得到K30,具体流程如下:
1)在L30引入差分故障11 11 11 11,得到故障密文:c7 89 c4 9c 10 2d 3f d6。通过k31得到31轮加密后的密文:10 2d 3f d6 69 38 16 bb。将故障密文同正确密文异或得到:af ba be d1 11 11 11 11。将密文差分af ba be d1通过逆P置换、逆列混淆后得到S盒的输出差分:77 ec 9b 87。
2)在L30引入差分故障aa aa aa aa,得到故障密文:f0 3c 68 d4 c1 2a 77 ab。通过k31得到31轮加密后的密文:c1 2a 77 ab d2 83 ad 00。将故障密文同正确密文异或得到:7e bd f6 ac aa aa aa aa。将密文差分7e bd f6 ac通过逆P置换、逆列混淆后得到S盒的输出差分:33 86 11 33。
3)结合表确定出S盒未加故障时的输入:每一个未知的输入候选值均只有一个交集,这样就唯一确定出S盒的输入为:55 87 b1 f5。
4)将S盒输入:55 87 b1 f5与31轮后密文右半部分:78 29 07 aa异或得到k30:2d ae b6 5f。从而得到30轮加密后的密文:78 29 07 aa 66 95 d0 da。
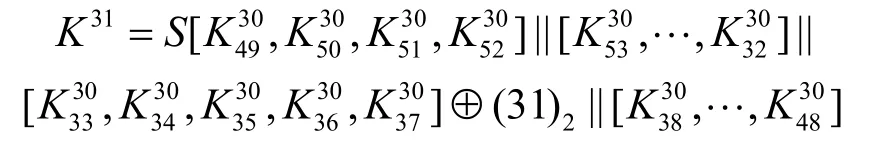
实验中得到k31是K30的高位32 bit,去掉重复比特,经过两次密钥扩展,可得到K30的15+32= 47 bit,剩余17 bit可以通过遍历求取,数据复杂度为217。
4 结束语
本文分析轻量级分组密码算法S盒差分传播特性,通过建立<输入差分、输出差分、可能输入值>的对应关系表,利用不同故障条件下故障差分对应的输入值集合交集唯一的特性,针对基于Feistel结构的MIBS算法,分别在第30轮和31轮注入两次故障,可以恢复47 bit轮密钥,进而通过穷举恢复其余密钥比特,时间复杂度为217。

