基于零相位频率的晶体谐振器等效电参数测量方法

刘 东，黄显核，唐苑琳，王 艳

(1.电子科技大学自动化工程学院 成都 611731；2.西南石油大学电气信息学院 成都 610500)

晶体谐振器广泛应用于振荡器设计[1]、时频控制[2]等领域。晶体谐振器也应用于传感器领域，如温度传感器[3]、石英晶体微天平[4-7]等。

1 介绍

晶体谐振器等效参数的测量方法很多，工程上通常先测量谐振频率和负载谐振频率，再求解等效参数。国际电工委员会(International Electrotechnical Commission, IEC)推荐采用矢量网络分析仪测量等效参数[8]，国内也有采用网络分析仪测量等效参数的报道[9-12]。这些方法都存在理论误差，在谐振器Q值较低时，理论误差变大。

本文提出了一种基于零相位频率测量等效参数的方法，该方法没有采用近似计算，而是采用正向计算过程，可以一次计算出4个参数，操作简单。

2 晶体谐振器BVD模型的零相位频率

图1a为晶体谐振器BVD(Butterworth-Van Dyke)等效模型串联负载电容CL。其中R1为动态电阻、L1为动态电感、C1为动态电容、C0为静态电容。通常认为晶体谐振器BVD等效模型的谐振频率只与动态电感L1和动态电容C1有关，并且有：

式(1)中只包含L1和C1，因而，通过频率只能求解L1和C1。通过推导，本文得到BVD等效模型零相位频率的精确形式为：

式中，

式(2)中取正号即得到反谐振频率[13-14]取负号即得到谐振频率fr。由式(2)可知，频率和4个等效参数都有关。因此，可以通过频率求解4个等效参数，而不仅仅是两个等效参数。由于有4个待解参数，除了fa、fr之外，还需要两个频率，以便于构建四元方程组。这里选择负载反谐振频率fA与负载谐振频率fR。

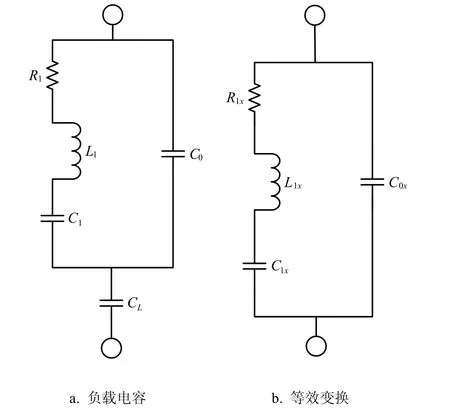
图1 晶体谐振器串联负载电容及其等效变换

为了简化求解负载反谐振频率与负载谐振频率的过程，先做一个等效变换。图1a模型可以等效变换为图1b模型的形式，并且这种变换不受谐振器参数限制[15]，因而低Q值谐振器也适用于此种变换。变换之后，的函数。将变换关系带入式(2)，即得到负载零相位频率为：

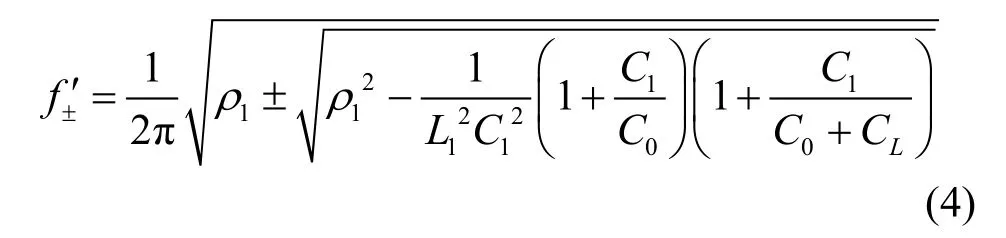
式中,

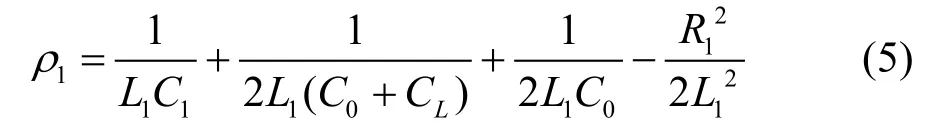
式(4)中取正号即得到负载反谐振频率fA，取负号即得到负载谐振频率fR。

3 等效参数的测量方法

由fa、fr、fA、fR即可构建四元方程组。观察式(2)可见，fa、fr存在内在联系，其平方和就是式(3)的形式，即：

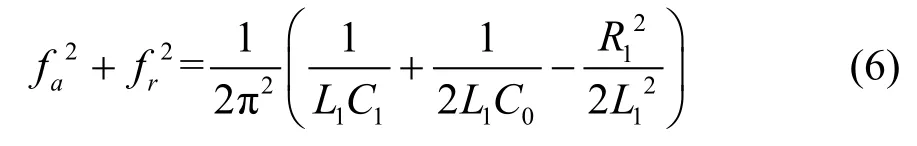
同理可得：

将式(6)带入式(2)得到：

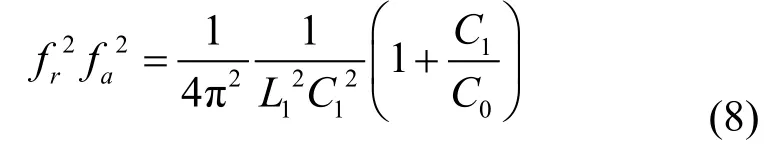
同理可得：

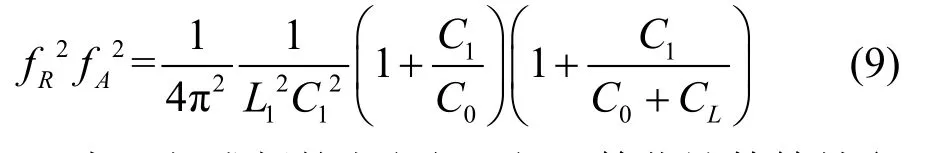
式(6)～式(9)组成新的方程组，便可简化计算等效参数的过程。求解上述方程组，可依次得到：

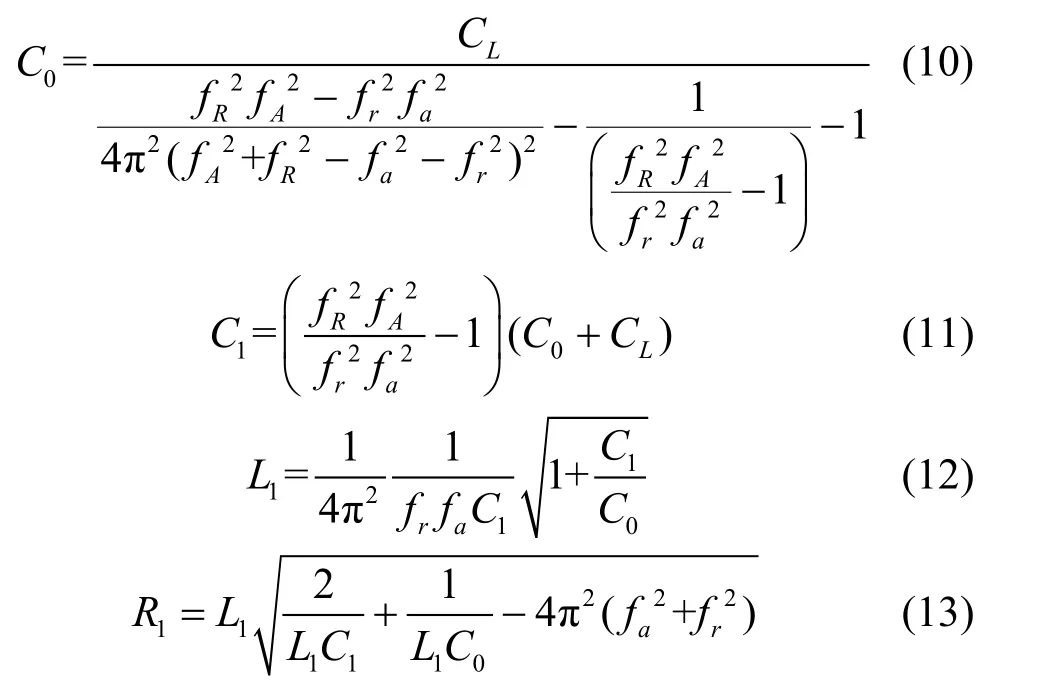
4 ADS仿真验证

本文采用安捷伦仿真软件ADS(advanced design system)进行仿真，以验证式(10)～式(13)。图2是仿真原理图，其中谐振器参数[16]设置为R1=13.764 Ω、实测实验中，串联了负载电阻以削弱接触电阻的影响。因此，仿真中串联了负载电容Rx。

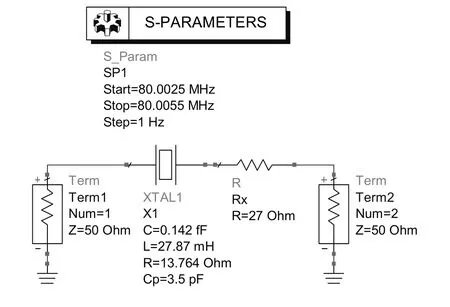
图2 仿真原理图

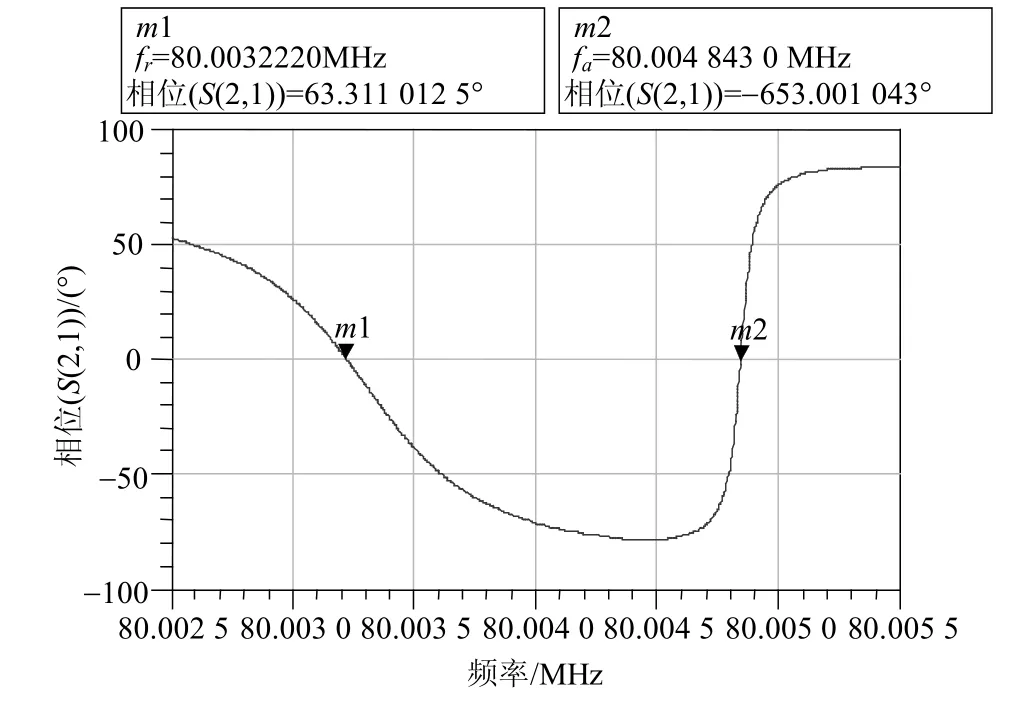
图3 仿真结果

图3 是仿真结果图。通过图3，可读出两个零相位频率，即fr=80 003 222 Hz，fa=80 004 843 Hz。同理可得到串联电容CL=10 pF时，fR=80 003 644 Hz，由于fa和fA有效位数不够，导致fa=fA，实际它们是不一样的。为了防止逻辑错误，增加了fa的有效位数，得到fa=80 004 843.5 Hz。将数据带入式(10)～式(13)得到：R1=16.798 Ω，计算参数和设置参数接近，但是有差距。增加频率的有效位数至0.1 Hz，得到：R1=15.066 Ω，L1= 27.878 mH，增加频率的有效位数至0.001 Hz，得到R1=13.884 Ω，L1=27.871 mH，可见频率越精确，计算值与设定值越接近，即计算参数收敛于设定参数。因此，本文方法在理论上是正确的。

5 实测实验

图4是安捷伦网络分析仪E5062A实测的晶体谐振器相位-频率曲线，所测晶体为10 MHz、SC切石英晶体。供应商提供的参数为：R1=69.78 Ω，L1=1 407.29 mH，C1=0.18 pF，C0=2.11 pF。其Q值较大，因而本文方法测量结果应该和标称结果很接近。图中，相位偏移为-45.7°，这是由于导线长度等问题产生的。

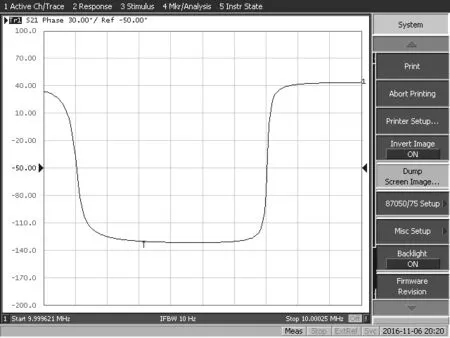
图4 安捷伦E5062A实测相位-频率曲线

由图4可见，相位-频率曲线在谐振点附近的斜率很大，在1 Hz以内相位可以变化几度。如，距离fa最近两点的相位分别为10.02°和-5.57°。它们和零相位仍有较大差距，所以本文采用线性插值的方法来间接测量零相位频率。此时测得：fr=9 999 717.0 Hz，fa=10 000 095.3 Hz。同理可得，fR=9 999 957.9 Hz，fA=10 000 088.1 Hz。同时，为了消弱接触电阻对测量的影响，本文串联了一个电阻RX=27 Ω。

实测过程中发现存在一个随机漂移频率fx使本文选择相频曲线在fr和处的导数方程来修正此随机频率。导数方程为：

式中，

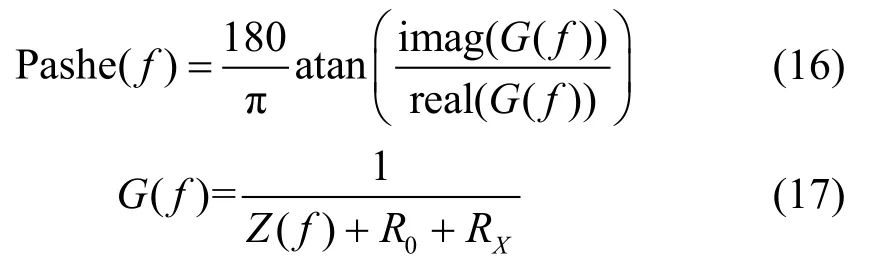
式中，Z是谐振器的阻抗；R0是网络分析仪的内阻，这里R0=100 Ω。

由式(10)～式(15)组成了六元非线性方程组，即可求解等效参数以及随机频率fx和负载电容CL。本文采用二维搜索法求解此方程组。

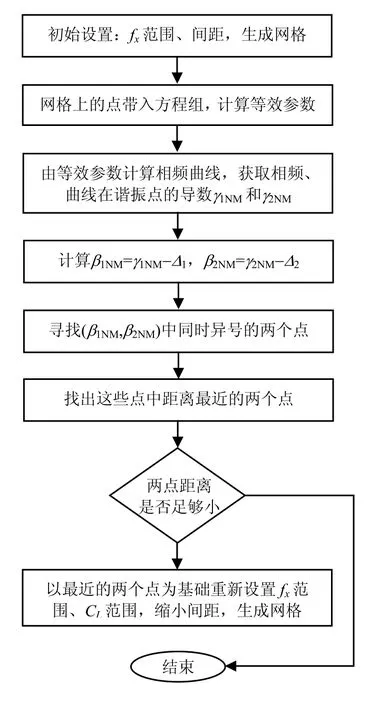
图5 解非线性方程组流程图

其具体的过程为：

1)和有限元解法类似，首先生成一个包含fx和的二维网格。初始值为间距为f_bu。CL初始值为间距为则网格上的点为

3)由等效参数计算相频曲线，由相频曲线得到谐振点的导数γ1NM和γ2NM。

4)计算误差：β1NM=γ1NM–1Δ，β2NM=γ2NM–2Δ。则，网格上的每个点都有对应点(β1NM,β2NM)。

5)寻找(β1NM,β2NM)中的两组点(β1nm,β2nm)和(β1xy,β2xy)同时满足下列两个条件：β1nmβ1xy＜0，其中，(β1nm,β2nm)对应点对应点

7)判断这两个点的距离是否足够小，并满足精度要求。满足计算结束，不满足以这两个点为基础重新设置fx和CL的范围。缩小间距再次生成网格。重复流程2)～6)，直到满足要求为止。

上述过程的流程图如图5所示。

图6 实测与复现相频曲线

串联180 Ω电阻，即RX=180Ω时所测量参数为：

两组实验的测量值和标称值都很接近，RX=180 Ω时更接近标称值。这可能是因为还有接触电阻等不确定电阻的存在，串联电阻越大，不确定电阻的影响越小。测量值与标称值之间略有差距，可能是由于测试环境(如测试温度、测试夹具的静电容等)与供应商测试环境不一致。

6 结束语

本文推导了晶体谐振器零相位频率与负载零相位频率的精确形式，提出了一种基于4个零相位频率测量谐振器等效电参数的方法。该方法的理论正确性通过ADS仿真实验得到验证，实测实验也表明该方法是可行的。该方法没有通常测量动态电阻中的往复测量过程，因而操作简便。该方法不包含近似计算，因而也适用于谐振器Q值较低的情况，如石英晶体微天平、微机电系统等。