旋磁各向异性非均匀球体电磁散射特性

曹 雷，康 凯

(电子科技大学电子工程学院 成都 611731)

针对各向异性媒质的光或者电磁散射特性研究一直都是物理界和工程界的研究热点，因为各向异性媒质在光学、生物学、医学以及纳米科学等领域都有着广泛而有前景的应用。文献[1]提出了均匀球形媒质对于平面波的散射理论，称之为Mie散射理论。随后许多研究者在Mie散射理论基础上对各向同性多层非均匀球体的电磁散射特性进行了研究[2-3]。除了对各向同性媒质散射特性的研究，研究者还根据Lorenz-Mie散射理论，应用不同的方法给出了各向异性媒质中电磁场的解析解，如：并矢格林函数结合变化的球矢量波函数的方法[4]，应用球矢量波函数结合傅里叶变换的方法[5-6]，T-矩阵方法[7-8]。近几年，学者们也提出了一些新的方法用于对各向异性媒质电磁特性的研究，如：使用频域鞍点估算法对外加单轴电各向异性涂层电大尺寸复杂目标散射场的计算[9]，非均匀各向异性目标电磁散射的Nystom解[10]，各向异性媒质的光学定理[11]，尺度变换方法[12]，应用状态空间法对双轴双各向异性媒质电磁特性的研究[13]。应用球矢量波函数结合傅里叶变换的方法对不同结构的球形等离子体的电磁散射特性进行了研究，包括：等离子各向异性球体[14]，等离子各向异性球壳[15]以及等离子各向异性非均匀多层球壳[16]。文献[17]根据球矢量波函数的完备性与正交性给出了光各向异性磁性球体中电磁场的解析解，其方法避开了冗长而复杂的积分运算，在数值精度上有较大的优势。随后文献[18]将该方法应用在旋电各向异性球体的研究中，给出了完整的理论公式和数值结果。

本文将文献[17]的方法进行推广并用于研究径向非均匀多层旋磁介质球的电磁散射特性。具体地，根据Lorenz-Mie散射理论和球矢量波函数理论，多层球球心区域的电磁场被展开为第一类球矢量波函数的线性叠加，球壳区域电磁场展开为由第一类和第三类矢量波函数的线性叠加。而入射场和散射场分别由第一类和第三类球矢量波函数进行展开。最后在不连续表面匹配边界条件得到各个区域的展开系数以及散射系数。随后，计算了非均匀旋磁球体的双站雷达散射截面，并与有限元法得到的数值结果进行对比，结果吻合很好，验证了公式推导的正确性和有效性。最后给出了几个新的算例，用于分析旋磁各向异性多层球体的物理特性以及在减弱和加强雷达散射截面中可能的应用前景。

1 基本模型

根据文献[17]，旋磁介质球中的电磁场在球坐标系下可以表达为具有不同特征值kl的球矢量波函数的线性叠加，具体的H和E的表达式为：

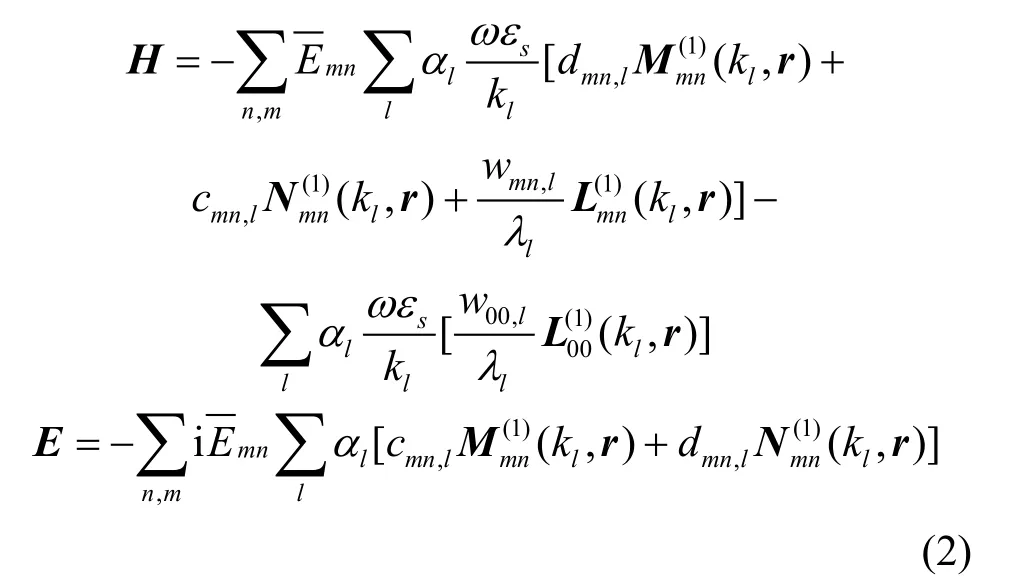
将文献[17]用于研究径向多层结构的旋磁各向异性球体。图1为径向多层非均匀球形结构的平面图。层数N可以取任意值。散射体置于自由空间中，球心与坐标原点重合。区域0为自用空间，其介电常数和磁导率分别为0ε和0μ。而对于区域p，其电磁参数分别为εps和其中表达式和完全一致，除了用于标记区域的下标

2 多层旋磁球内部场展开式

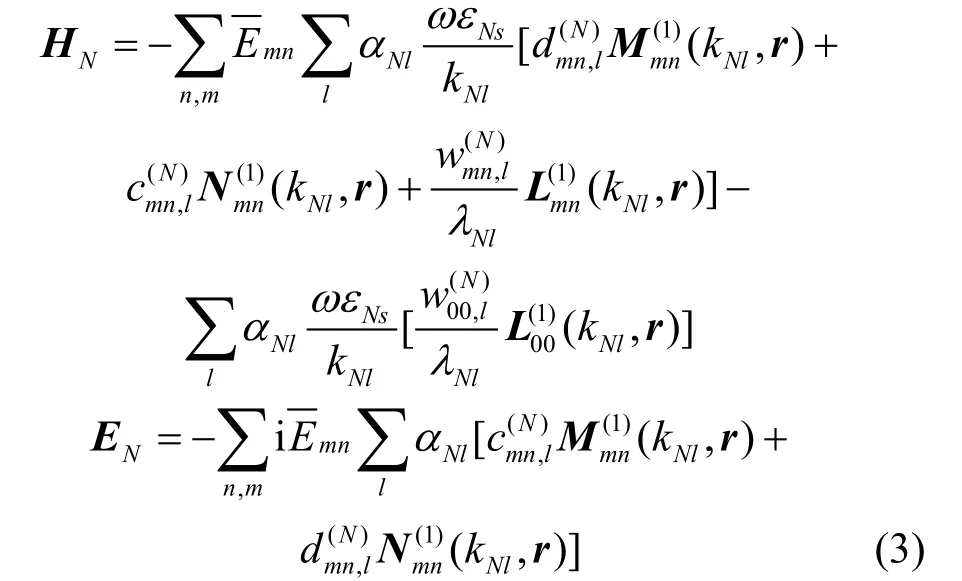
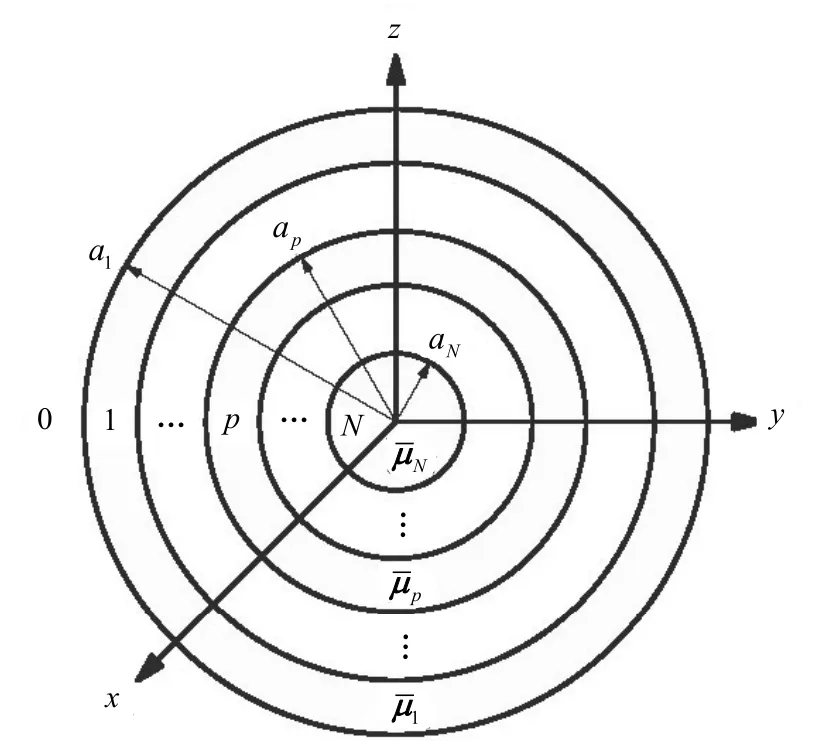
图1 多层球形结构的几何模型

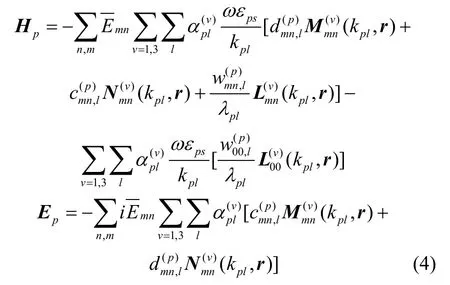
3 散射场和入射场的展开

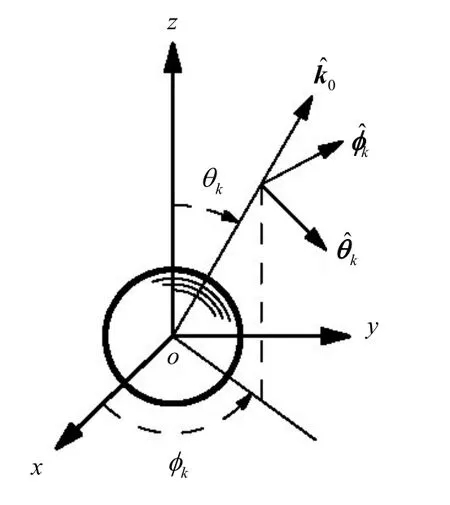
图2 平面波照射到球体的球坐标系示意图

图2 为平面波照射到球体的球坐标系示意图。自由空间中的散射场与Mie理论中的表达式相同[19-20]，根据矢量波函数理论，可将散射场展开为：

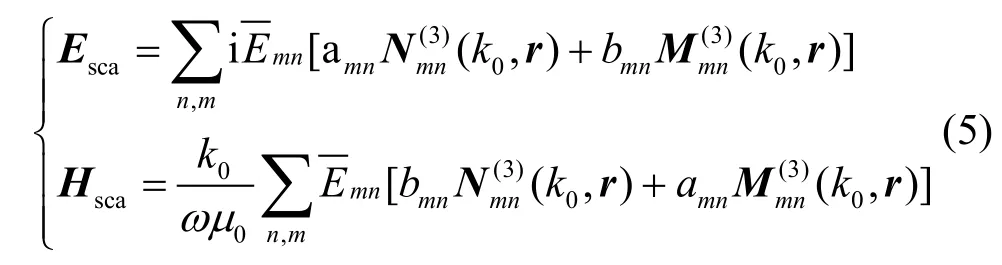
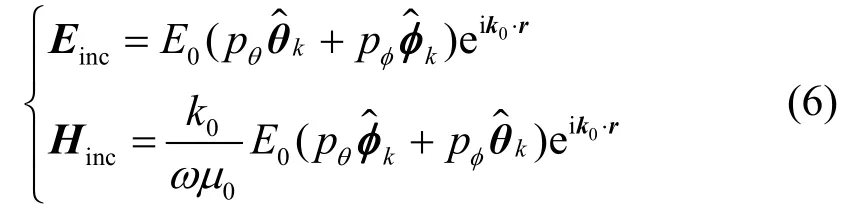
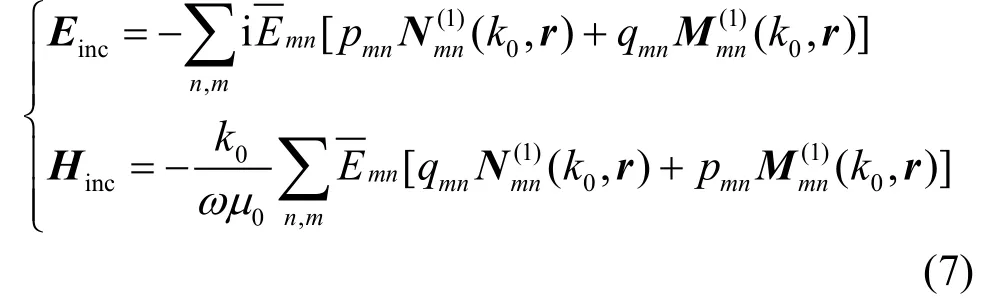
式中，展开系数pmn和qmn可以在文献[17]中找到；双求和符号中的下标n的取值为1～nc(截断常数)；对应每个n，m的取值为-n～n。

4 匹配边界条件

入射场、散射场、以及球体内部各个区域场都已展开为球矢量波函数的叠加形式。下面通过匹配边界条件来确定各个内场区域的展开系数以及散射系数。在不连续表面根据电磁场切向连续性，可以得到：

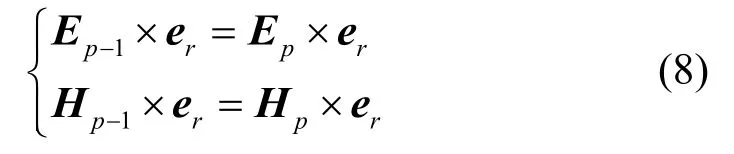
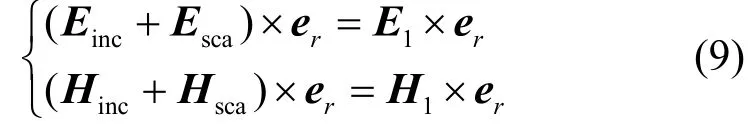
将电磁场展开式(4)带入式(8)，经过化简，并考虑等式两边对应分量相等，可以得到以下矩阵递推公式：

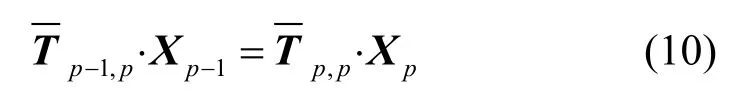
T中的矩阵元素具体为：

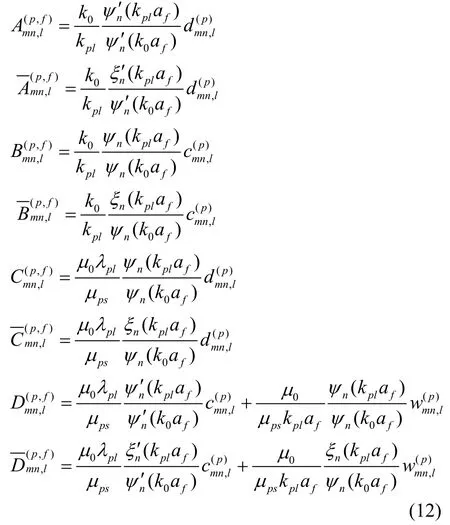
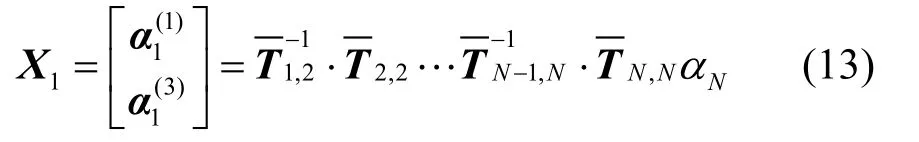
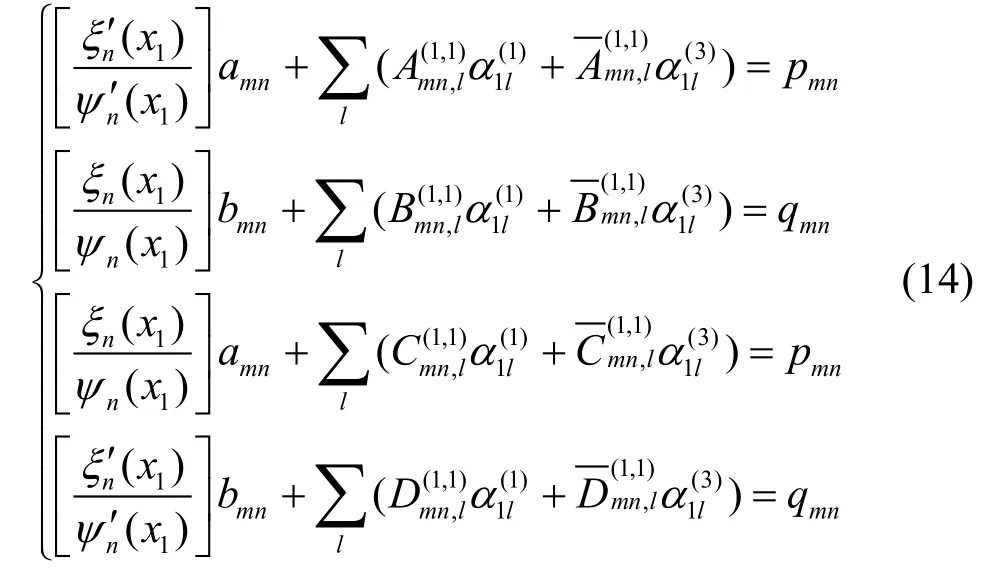
将式(13)代入式(14)，并求解线性方程组，可以得到散射系数以及球心区域展开系数Nα。根据递推关系式(10)，当求得展开系数Nα后，可以采用由内向外递推的方式以获得区域N-1到区域1的场展开系数。并且，根据已经求得的散射系数amn、可以对雷达散射截面进行计算，其定义为[21]：

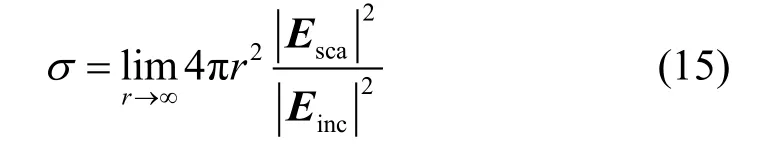
当r→∞时，球矢量波函数在远场的近似表达式可以在文献[22]中找到。

5 数值结果

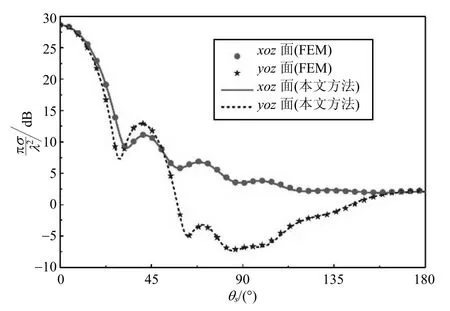
图3 2层球形结构的归一化雷达散射截面数值结果与有限元方法计算结果的对比图

通过数值计算对旋磁非均匀介质球的雷达散射截面进行分析和讨论。根据已经得到的公式，可以计算空间任意点的场值。对于入射场，假设其幅度为1，极化方向沿着x轴，传播方向为z轴正方向，即球体结构的大小由电尺寸所描述介电常数统一假定为其中由Lorenz-Mie理论知道，线性展开式(3)和式(4)是收敛级数，因此可以对展开式进行截断以便于实际的计算。本文的截断常数为

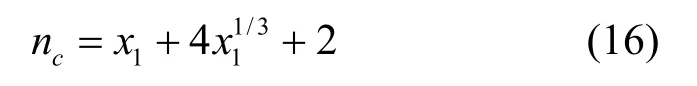
实际计算中，递推式中不同区域的矩阵T需要有相同的维度，那么各个区域中电磁场展开式的截断系数nc应该具有相同的值，为了获得足够的精度，本文采用最大电尺寸x1计算截断常数nc。

为了验证本文公式的正确性和有效性，首先将2层旋电介质球雷达散射截面的数值结果同有限元仿真结果进行对比，观察到雷达散射截面在E面和H面都具有很好的吻合，如图3所示。其中电尺寸为：x1=2π,x2=1.5π；材料参数为这在一定程度上证明了公式的正确性和数值计算的有效性。下面给出3个新的算例研究该散射结构的远场特性，并分析材料参数rμ和κμ的改变对雷达散射截面的影响。

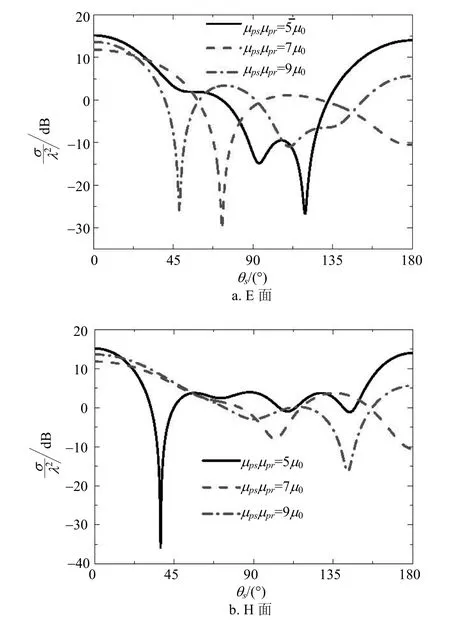
图4 3层单轴各向异性球体在E面和H面的双站雷达散射截面

图4给出了3层单轴各向异性磁球在E面和H面的双站雷达散射截面图，电尺寸和材料参数为：其中根据不同的画出了3条雷达散射截面曲线图。由图4可以看出，当的值从50μ增加到90μ时，E面的谐振角往左有明显的偏移，而在H面，谐振角往右有着明显偏移。

图5给出了3层旋磁各向异性球在E面和H面的雷达散射截面图，该散射结构的电尺寸和图4相同，对于每一层的电磁参数，选取了4组参数，变化范围为从图5可以看出随着的增加，E面和H面的雷达散射截面有着不规则的变化。因此可以预见通过改变的值来对散射场进行控制有困难。

图6给出了一个中等电尺寸的5层无耗旋磁媒质球在E面和H面的雷达散射截面，材料参数为表1所示。从图6可以看出，当电尺寸变大以后，雷达散射截面曲线变得十分振荡，这与图4和图5有所不同。同时也可以看出当入射波长和散射体大小相当时，雷达散射截面图的分布特性。

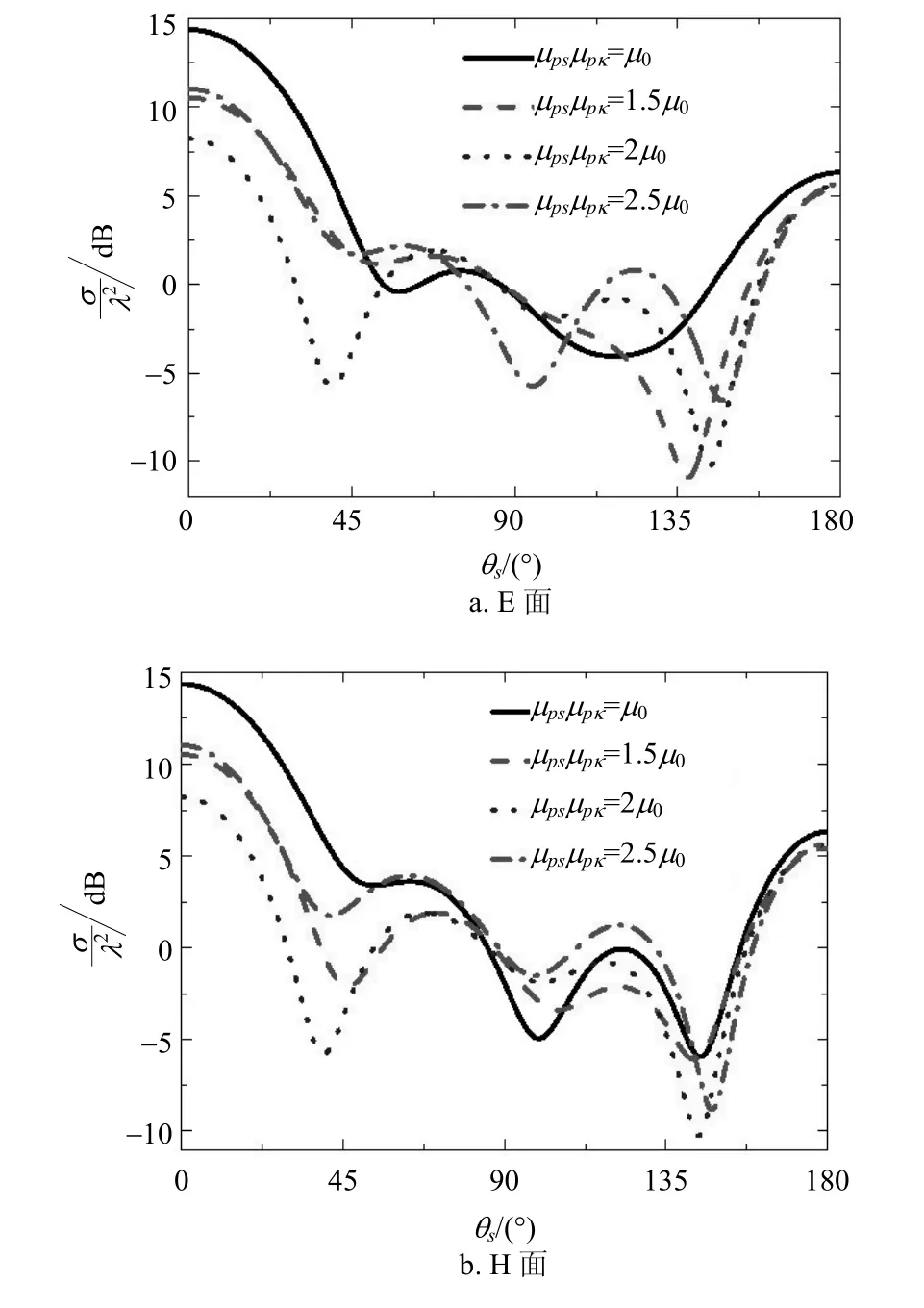
图5 3层旋磁各向异性球体在E面和H面的双站雷达散射截面

表1 5层无耗旋磁各向异性球体的电尺寸以及材料参数

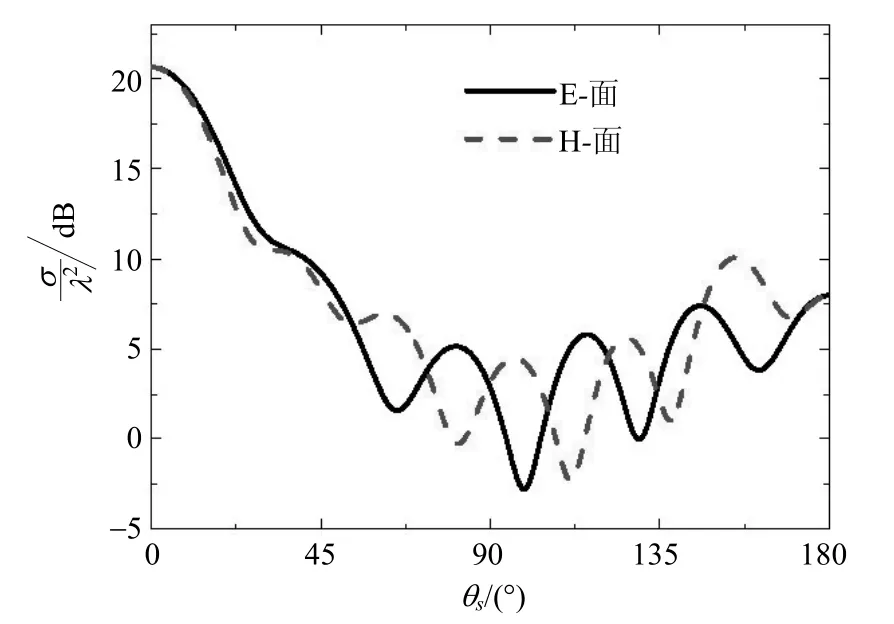
图6 5层无耗旋磁各向异性球体在E面和H面的双站雷达散射截面

6 结束语

本论文以T矩阵方法为基础，得到了旋磁各向异性非均匀球体散射特性的新的解析解。根据 Lorenz-Mie 散射理论，入射场、散射场以及球体内部各区域的场被展开为球矢量波函数的线性叠加形式。通过在非连续表面匹配边界条件得到各区域场的展开系数以及散射系数。通过与有限元法计算得到的雷达散射截面数值结果进行对比，很好地验证了本文公式的正确性和有效性。最后通过几个算例对该模型的电磁散射特性进行了详细分析和讨论。对于旋磁材料，利用球形多层非均匀结构，可以实现对雷达散射截面的增强或者减弱的优化设计。