基于马尔科夫预测的时分复用弹性波带交换算法
孟凡博 ,巩小雪,郭 磊,张 旭
(1.东北大学计算机科学与工程学院 沈阳 110819;2.国网辽宁省电力有限公司 沈阳 110006)
弹性光网络中,频谱被分割成许多粒度小、相互正交的子载波。通过分配适量子载波完成业务传输,包括业务疏导、路由和频谱分配[1-10]。其中,业务疏导能够实现多个细粒度业务(一组业务)对同一载波资源的共享。此外,为实现更加高效利用频谱的业务疏导,在时分复用弹性光网络中,可为多个业务组分配不同的时隙,使各业务组在不同时间段内占用相同的载波,进一步优化资源利用。
马尔科夫预测模型指出未来情况只与当前状态有关。对于时分复用弹性光网络,在已知业务连接保持时间前提下,通过此模型预测未来业务占用时隙数,方可优化路由与频谱分配。此外,波带交换[11-15]在实现业务疏导、路由和频谱分配基础上,以“多业务信道捆绑”方式,减少光交换端口数量。现有针对弹性光网络业务疏导、路由和频谱分配的工作均未考虑时间预测模型与波带交换的技术融合优势。为此,本文建立基于马尔科夫的时隙占用预测机制,给出相应的时分复用弹性波带交换算法。通过时间预测及波带交换进一步优化时分复用弹性光网络的业务疏导、路由和频谱分配性能。
1 基于马尔科夫的时隙占用预测机制
动态业务连接请求是随时建立和释放的,这导致频谱占用状态可在业务连接保持时间内变化。可根据离开事件历史信息去预测未来业务占用时隙数,进而完成时隙分配。
占用波带b′子载波Fs′的第i个业务连接剩余时间如式(1)所示。其中,〉分别表示占用波带b′子载波Fs′的第i个业务连接建立和保持时间;〉分别表示即将到达业务连接建立和保持时间。
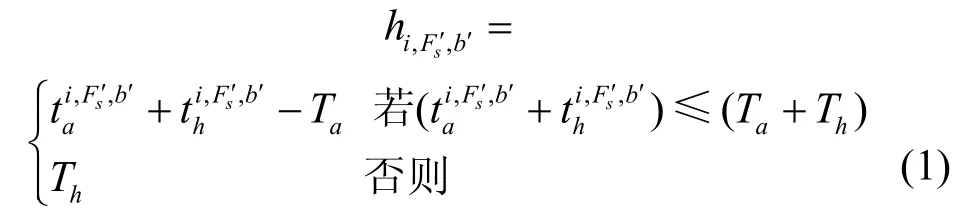
为预测时隙占用情况,用马尔科夫链描述业务连接请求的到达与离开,如图1所示。
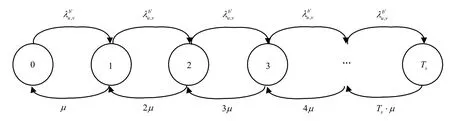
图1 请求到达/离开状态转移图
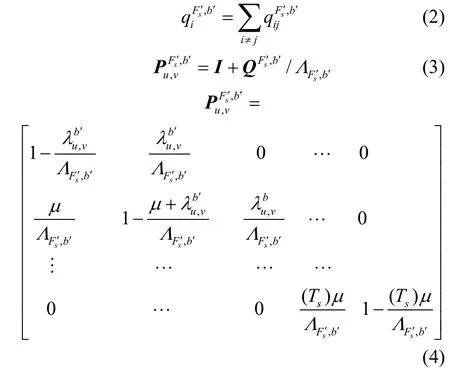
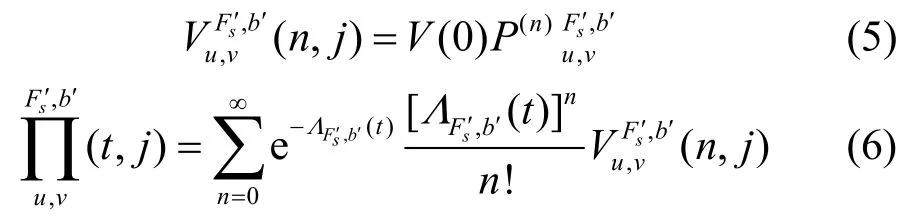
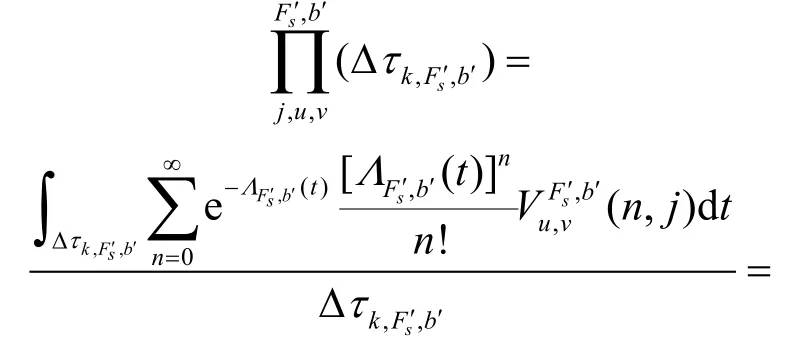
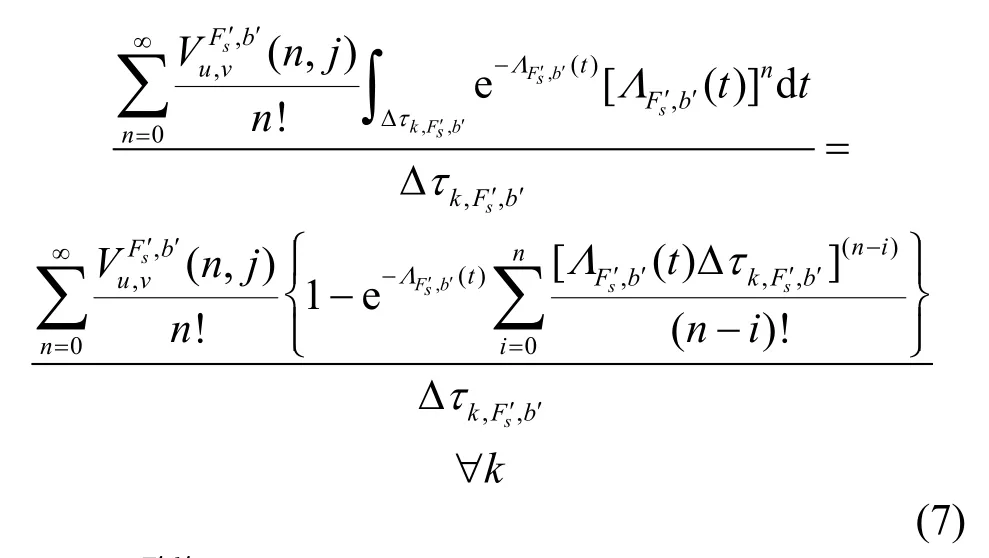
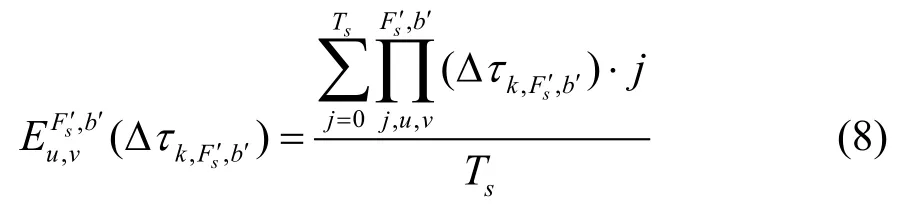
将每个时间间隔内的子载波占用期望求和,可得链路(u,v)波带b′子载波Fs′上即将到达业务连接保持时间Th内可能占用的时隙数为:
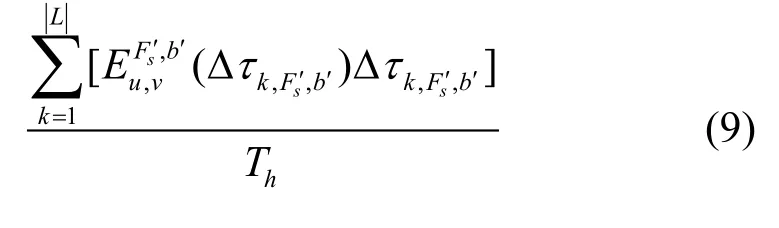
2 基于马尔科夫预测的波带交换算法
根据式(9)预测即将到达业务连接保持时间Th内可能占用的时隙数,并结合系统中已有业务连接求得链路负载。此外,根据式(10)计算链路(u,v)负载时,考虑了未来可能占用时隙数及链路中已有业务连接。这里,1δ,2δ分别表示占用时隙数与链路固有负载′的权重系数。整条路径开销则可通过式(11)计算。
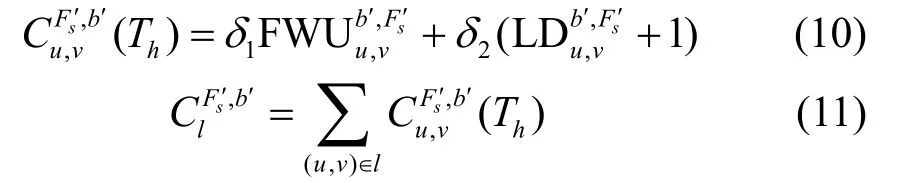
显然,链路开销小者越易被选中。若1δ小于2δ,则优先选择多个业务在不同时隙共享载波资源的链路,则算法所采用的时分复用性能优势更加明显;反之,则优先选择更多业务被同一波带所承载的链路,则算法所采用的波带交换性能优势更加明显。
RSBMA-EEU-TDM算法步骤如下:
1)输入网络拓扑及网络状态信息。
2)等待业务连接建立请求。
3)通过式(9)计算未来可能占用时隙数,从而计算链路负载。通过Dijkstra,根据式(11)为业务计算最短路径,并记录路径长度。
4)根据路径长度,并结合表1,选择恰当的最高调制级别。同时根据业务请求速率计算所占用的频隙数。
5)为业务分配频隙,若频隙不足,则阻塞该业务,并返回步骤2)。
6)将源与目的节点完全相同的业务传输路径捆绑进同一个波带中,并改变固定(波带)粒度N(波带能容纳的最多业务数)。
7)计算占用光端口总数及业务阻塞率。
RSBMA-SBN-TDM算法与RSBMA-EEU-TDM算法的步骤类似,仅在步骤6)中将具有相同子路径的业务传输路径捆绑进同一个波带中。
RSBMA-Balance-TDM算法同样采用上述步骤,但根据步骤7)和8)自适应调整波带融合策略。
8)设置不同的(W)权重系数,如(0.9, 0.1)(0.6,0.4),(0.4, 0.6)及(0.1, 0.9)等,统计综合反映占用光端口总数及频隙占用的性能参数W。W由式(12)得到。这里,P和Q分别表示采用和未采用波带融合的占用光端口总数,η表示占用频隙总数。

9)比较不同N值下W大小,得出使W最小的N值,最优化RSBMA-Balance-TDM算法性能。
注意,融入波带的多条传输路径相互独立,即分配给路径的调制格式和时隙不受其他路径影响。该约束可通过多粒度光交叉器的解/复用器来实现。
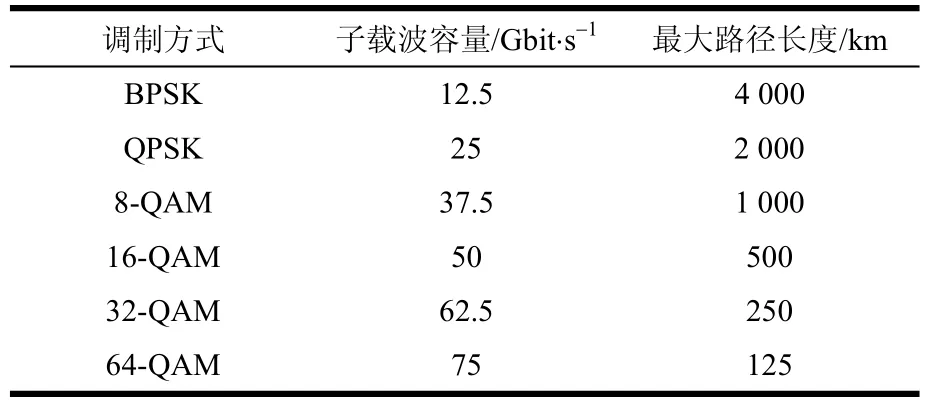
表1 调制方式对应最大路径长度关系[7]
3 实验评估
由于算法求解过程是NP完全的,为了评估所提算法的性能,本文采用如图2所示的、具有14节点和21条光纤链路的NSFNET拓扑进行仿真实验。基准比较算法是考虑业务疏导的RSA算法[8]。仿真中,本文假定1δ=2δ=0.5,即时分复用和波带交换对算法性能的提升同等重要。
图3a和图3b分别为设置权重系数(β,)α为(0.4,0.6)及(0.6,0.4)情况下,综合性能参数W随业务规模增加的变化情况。当(β,)α分别为(0.4,0.6)和(0.6,0.4)时,固定(波带)粒度N取为6的综合性能参 数W最小,即系统的综合性能最优。
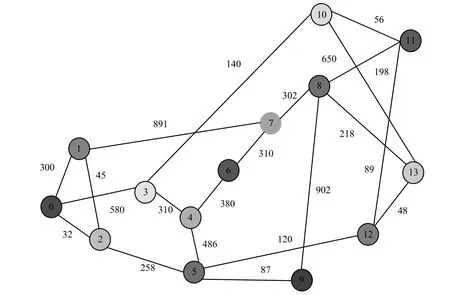
图2 NSFNET仿真拓扑

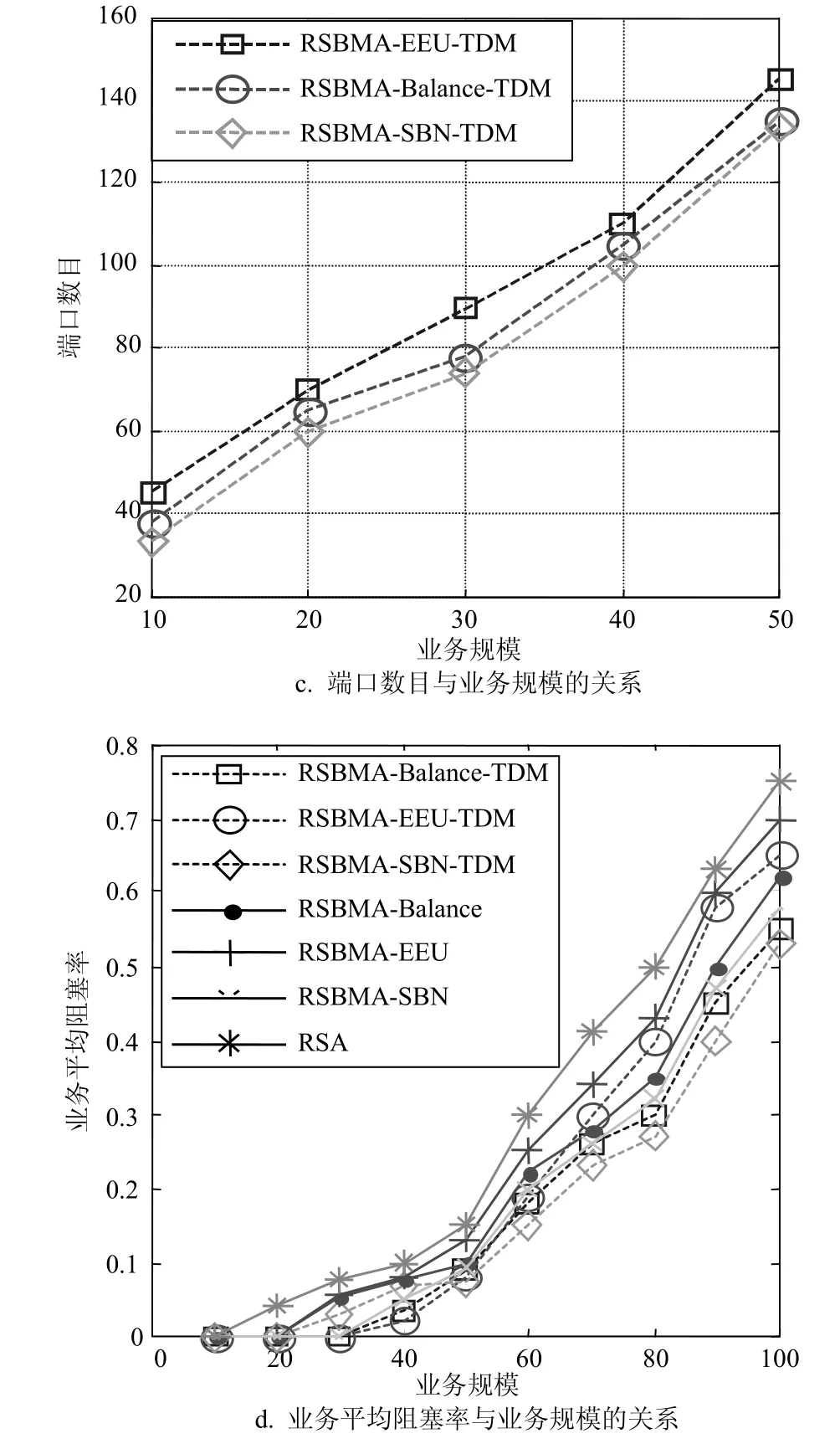
图3 算法性能仿真结果
由于已证明N=6时的RSBMA-Balance-TDM算法可使系统综合性能最优,在随后对RSBMABalance-TDM算法的性能分析中,取N=6。
图3c给出业务请求带宽在12.5~72.5 Gb/s之间随机选取,业务规模在10~50之间变化情况下,RSBMA-EEU-TDM,RSBMA-SBN-TDM,RSBMABalance-TDM 3种算法使用的光端口总数的变化情况。由于具有足够的频谱资源为业务提供服务,随着业务规模的逐渐增加,3种算法所使用的光端口总数均呈线性增长趋势。其中,RSBMA-SBN-TDM算法使用的光端口总数最少,而RSBMA-EEU-TDM算法使用的光端口最多。
业务规模在10~100之间的情况下各种算法的业务平均阻塞率如图3d所示。由图中可以看到,与传统RSA算法及普通RSBMA算法组相比,基于TDM的RSBMA算法组业务平均阻塞率相对较低,其平均改善率可达10%左右。
4 结束语
本文提出了基于3种不同波带融合策略的时分复用弹性波带交换启发式算法,并进行了仿真分析。仿真数据表明,调整波带粒度可使算法性能(即综合性能参数W)达到最优。同时,相比于其他算法,基于相同子路径波带融合策略的算法在使用光端口数量及业务阻塞率方面表现最优,但操作较复杂。通过RSBMA算法组与基于TDM的RSBMA算法组和传统RSA算法的性能对比,证明了基于TDM的RSBMA算法组能更加有效地降低业务阻塞率。

