基于邻域相似度的近邻传播聚类算法
赵 昱,陈 琴,苏一丹,陈慧姣
(广西大学 计算机与电子信息学院,广西 南宁 530004)
0 引 言
近邻传播聚类算法(AP)[1-3]本质上是一种基于中心的聚类算法,对特征规整的数据聚类效果较好,但对于特征复杂的数据辨识能力低,聚类效果较差[4-6]。针对此问题,有学者提出了相关改进,文献[7]通过进行局部聚类求得点簇集,提高聚类准确率;文献[8]通过对数据进行降维处理提高AP算法的精确度;文献[9]对大型数据集进行预处理,并结合CVM压缩和合并的方法提高算法的准确率;文献[10]使用核函数辨识数据特征,在一定程度上克服了AP算法对于数据集敏感的问题,但核函数的类型和工作参数对AP聚类精度有直接影响,需要优化以提高聚类精度[11]。
上述文献改进AP算法的思路是给偏向参数注入数据分布特征的先验知识,提高AP辨识聚类中心的能力,从而提高聚类精度。基于此思想,本文提出一种基于邻域相似度的近邻传播聚类算法(affinity propagation clustering algorithm based on neighborhood similarity,ZC-AP),用邻域相似度描述数据样本的空间分布特征,取代原AP算法的聚类度量作为新的聚类依据,并将邻域相似度作为数据样本的先验知识注入偏向参数,提高AP算法对复杂特征数据的聚类准确性。通过分析数据样本的统计特性,对数据概率分布曲线进行拟合,自适应地确定邻域半径和邻域密度,利用邻域相似度构建出相似度矩阵并求得偏向参数。最后在UCI数据集上验证本文算法的可行性。
1 数据样本邻域相似度的计算方法
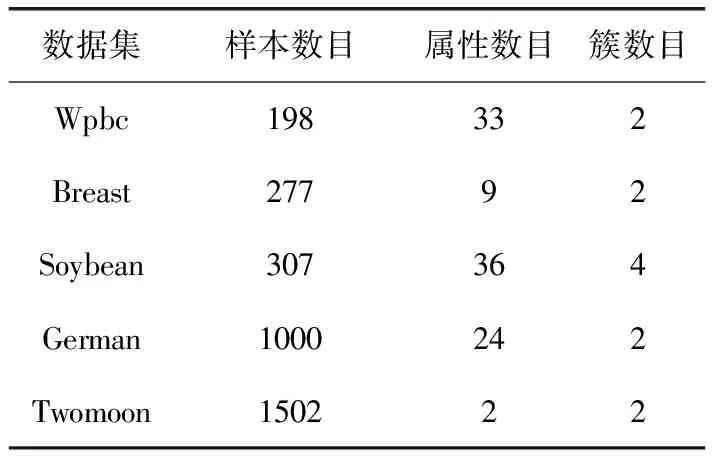
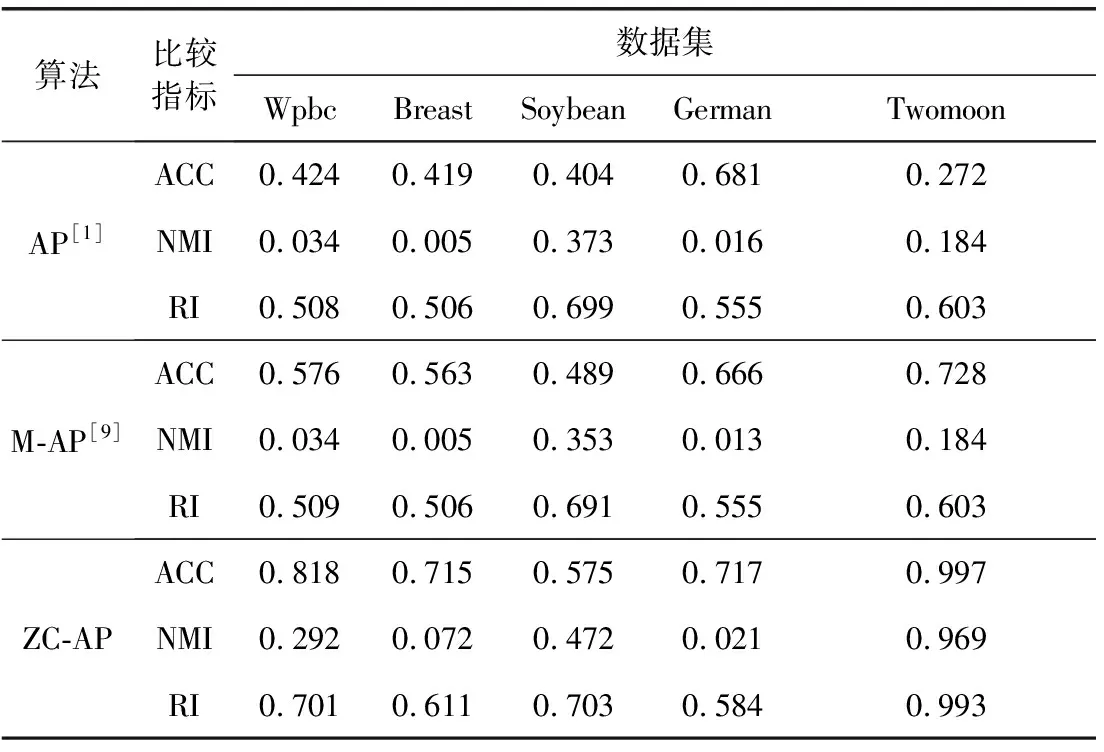
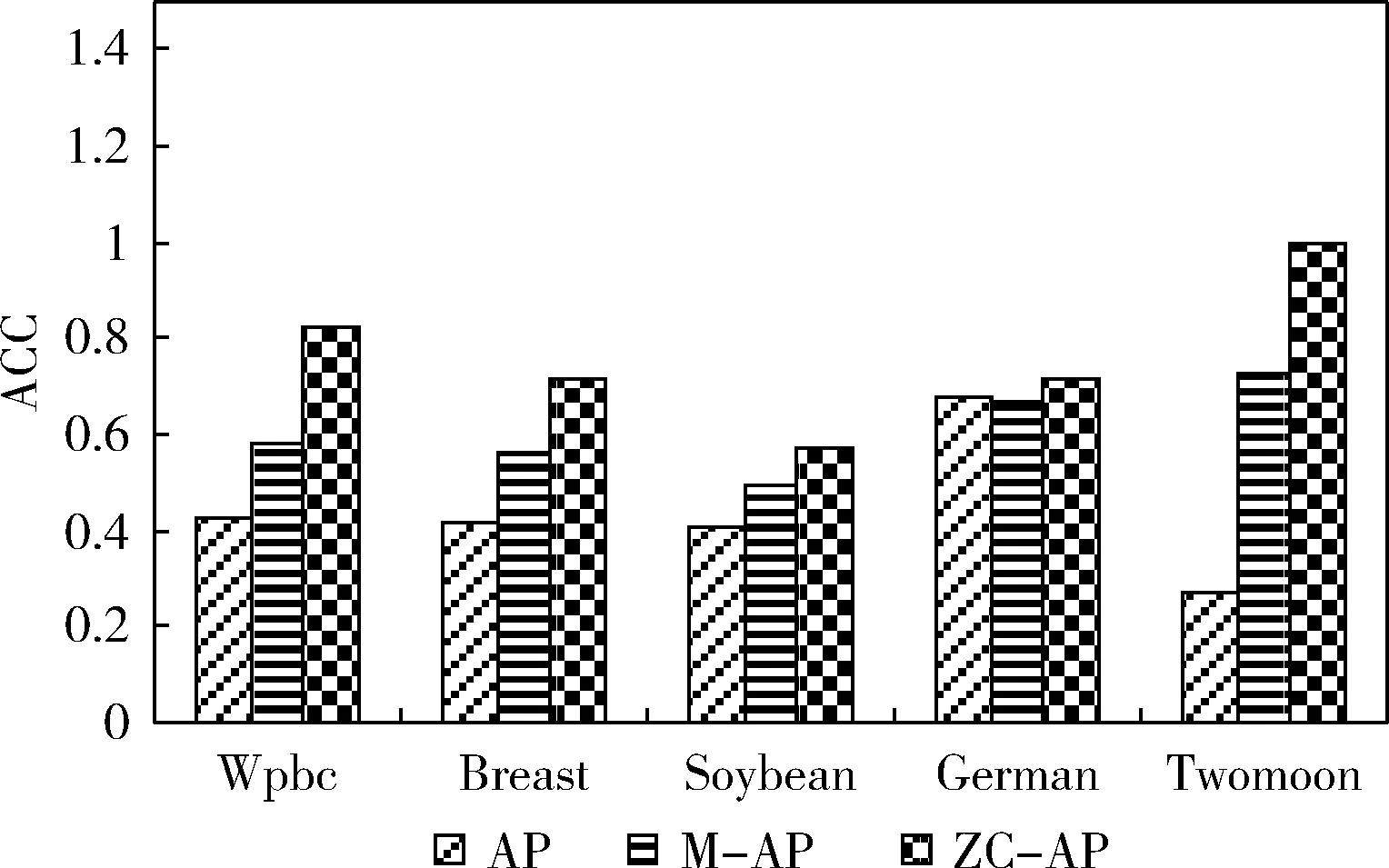
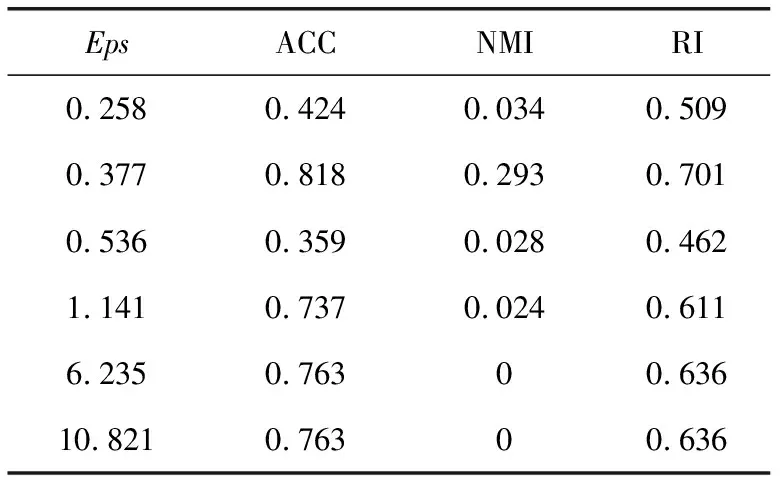
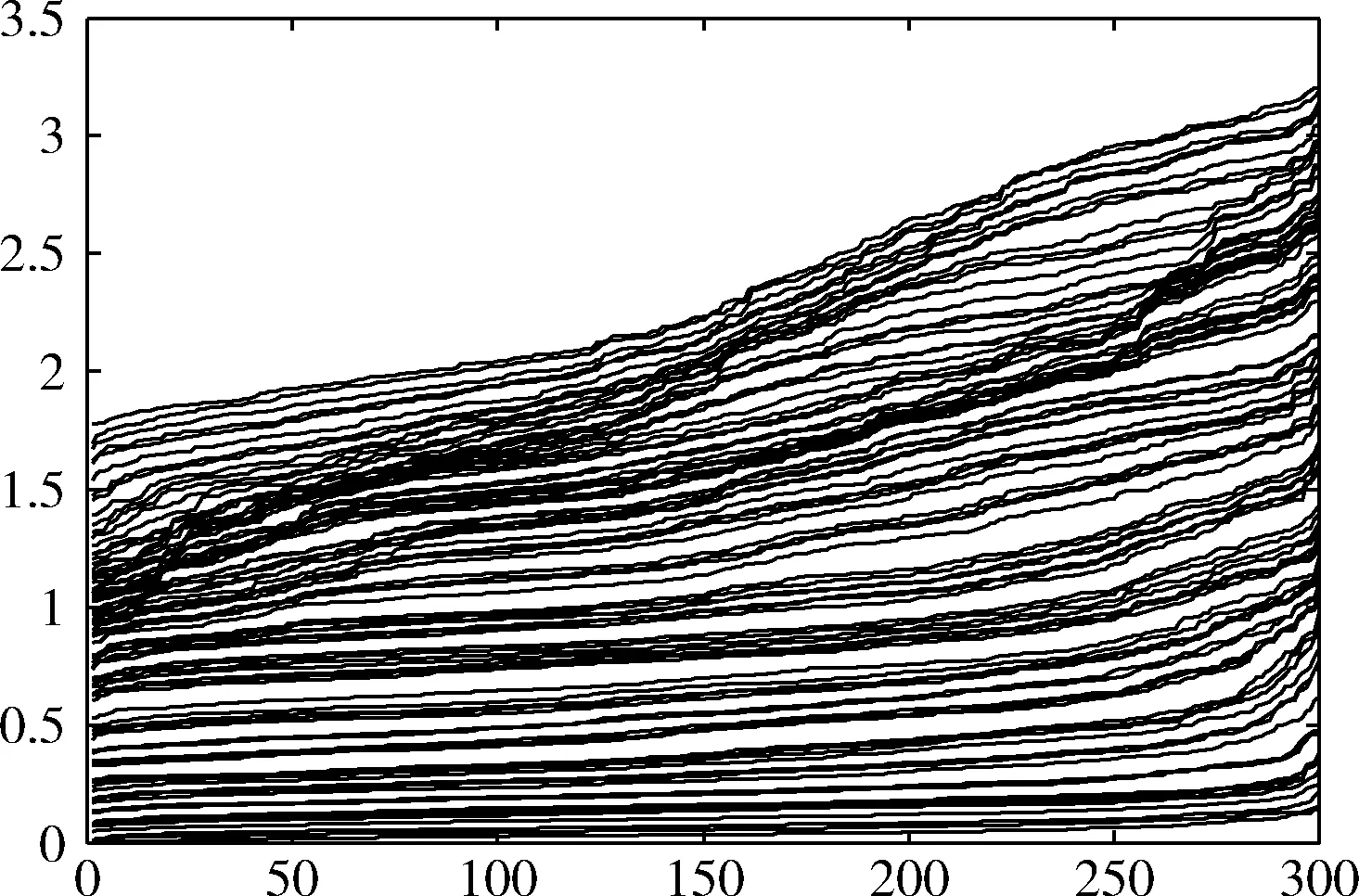
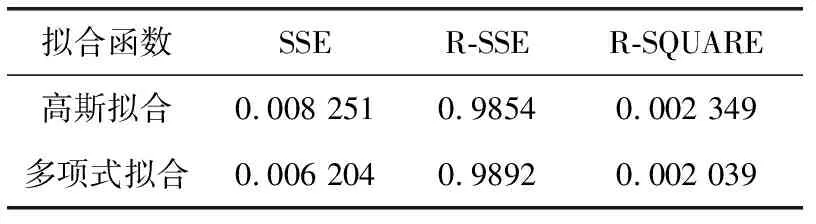
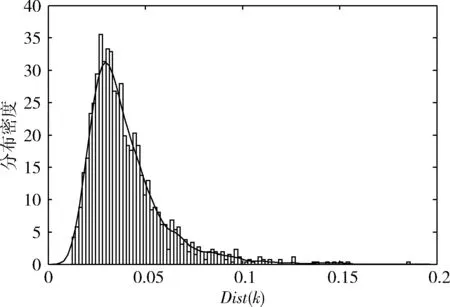
近邻传播聚类算法(AP)的基本思想是:对于数据集X={X1,X2,…,XN},使用距离公式计算相似度矩阵S,对支持度矩阵(responsibility,R)和归属度矩阵(availability,A)进行迭代更新,通过R和A筛选出聚类中心点。相似度矩阵S对角线上的元素S(i,i)称为偏向参数(pre-ference),它表示数据样本Xi成为聚类中心的可能性,此参数影响聚类中心的产生。初始时AP算法对角线元素S(i,i)取相同的值,表示每一个数据样本作为聚类中心的概率相同,记作:S(i,i)=p。在AP算法中,点间距离作为唯一的度量依据直接影响到S矩阵的构建、偏向参数的取值和R矩阵、A矩阵的迭代更新[12-14]。如图1所示,样本Xi、Xj、Xk的距离关系满足d(Xj,Xk) 图1 数据样本的密度分布 定义1 对于一个数据样本Yi,将Yi的Eps邻域 NEps(Yi)定义为以Yi为球心,以Eps为半径的多维超球体区域,即 NEps(Yi)={Yi∈D|dist(Yi,Yu)≤Eps} (1) 其中,D为多维实空间上的数据集,且D⊆Rd,dist(Yi,Yu)表示Yi与数据集中任意一个对象Yu的间距。选择的Eps越大,则该处数据点越稀疏,反之则数据点会越密集,所以如何选择合适的邻域半径对聚类效果十分重要。 定义2 对于数据集中的两点Yi和Yu,将Yi为中心,Eps为半径的区域看作一个圆,圆内包含的数据点数称为以Yi为圆心,Eps为半径的邻域密度,记做N1;同理,把以Yu为圆心,Eps为半径的邻域密度记做N2,将它们的交集即N1、N2相同数据点的集合定义为Rn Rn(Yi,Yu)= (2) 由式(2)可看出:Rn可能为空,也可能非空。当Yi、Yu所在区域密度较大,那么Rn也相对较大。 定义3 结合共同数据点集和欧氏距离,将数据集中点之间的相似度关系定义为邻域相似度Tn (3) (4) 其中,dist(Yi,Yu)表示Yi、Yu两点的欧氏距离,d为数据维数。邻域相似度Tn具有如下性质: (1)当两点相距很远时,它们共同区域中数据点的个数几乎为零,即Rn=0。邻域相似度Tn与欧氏距离类似,直接对数据点进行从属判断。 (2)当两点相距较近时,若它们共同数据点数较少,即Rn较小,此时Tn也会很小;若它们的共同数据点数较大,即Rn较大,此时Tn也较大。 对于复杂数据集,邻域相似度Tn能提高同一簇中各样本点之间的相似性,较传统欧氏距离更容易辨别数据特征。 用邻域相似度改进的AP算法流程如下: 输入:数据集V={X1,X2,X3…,Xn}; 输出:聚类中心的位置和个数; 步骤1 初始化算法的参数,包括:阻尼因子x,最大迭代次数maxits,连续收敛次数convits,初始化支持度和归属度矩阵。 步骤2 读入数据集,计算数据集中两点X1和Xk之间的欧氏距离,由此构建最近邻数据集合,对该集合的数据概率分布曲线进行拟合,求解导数与微分方程,求得密度半径Eps。 步骤3 求点X1和Xk的邻域密度,以及它们之间的相同数据点集Rn。 步骤4 通过式(3)求出Tn,从而构造相似度矩阵S,并求出偏向参数P。 步骤5 构造循环,进行以下步骤: (1)计算并更新支持度矩阵R (5) ri(i,k)=λ×ri-1(i,k)+(1-λ)×ri(i,k) (6) 其中 r(k,k)=p(k)-max{a(k,j)+s(k,j)} (7) (8) (2)计算并更新归属度矩阵A (9) ai(i,k)=λ×ai-1(i,k)+(1-λ)×ai(i,k) (10) (3)计算E=R+A,从E中寻找最大的数据样本即为聚类中心点。 (4)若该次迭代已经超过最大迭代次数maxits,或是连续convits次迭代聚类情况不发生改变,则迭代结束,否则继续进行迭代直到超过最大迭代次数或找到聚类中心点。 步骤6 输出聚类中心点的信息。 上述算法步骤中,步骤2较为关键,其细节说明如下。 由步骤2求得的最近邻数据集合绘制概率分布曲线,对距离的概率分布进行数据拟合,求取合适的Eps半径。选取常用的高斯拟合和多项式拟合函数进行数据拟合,其中,高斯拟合的公式为 f(x)=a×exp(-((x-b)/c)2) (11) 多项式拟合公式为 f(x)=axn+bxn-1+cxn-2+…+dx+e (12) 根据拟合结果,得到拟合组内方差SSE;均方根误差R-SSE;相关系数R-square[15,16];通过比较拟合精度和计算复杂度,选择合适的拟合函数进行计算。对于一个已知样本,通过以下步骤求其邻域半径Eps。 (1)首先计算数据集的距离分布矩阵 DISTn×n={dist(i,j)|1≤i≤n,1≤j≤n} (13) 得到一个n行n列的对称矩阵。 (2)进行列排序并转置得到KNNn×n矩阵 KNNn×n=sort(DISTn×n) (14) 为计算方便,去掉第一列的全零集合并进行列排序得到KNNn×(n-1)矩阵(以下简称KNN矩阵) KNNn×(n-1)=sort(KNN0n×n(1:end;2:end)) (15) (3)对KNNn×(n-1)矩阵的概率分布曲线进行数据拟合,得到拟合曲线。 (4)对拟合函数进行求解,去掉边界点得到所求Eps半径。 上述算法中,在AP算法的偏向参数中注入了数据样本之间相似度的先验知识,提高了AP算法对复杂数据特征的辨识能力。在步骤2中通过分析数据样本的统计特性自动求出邻域半径,提高了邻域相似度对不同数据集的自适应性。 在PC机上进行仿真实验,处理器为Intel Pentium G460(2.8 GHZ),内存8 GB,在Windows7 x64平台上用MATLAB实现算法。 选取以下3个指标对聚类算法的性能进行评价。 (1)准确率(accuracy,ACC) 准确率ACC表示聚类结果的正确率 (16) 其中,K为聚类结果的簇数目,Li表示聚类结果中第i簇内的数据样本能正确聚类的数目。聚类结果与真实类别个数完全相符时准确率为1,两者越不相符准确率越低。 (2)正则化互信息(normalized mutual information,NMI) 正则化互信息用来检验数据样本间的吻合程度 (17) 其中,K为簇数目,Ni和Nj表示第i、j个聚类的样本数目,N为样本总数,Nij表示第i个聚类结果与第j类的契合程度。NMI在[0,1]内取值,该值的大小表示聚类结果与真实情况吻合度的高低。 (3)芮氏指标(rand index,RI) 芮氏指标是在聚类结果与真实簇间关系未知时的准确性评价指标[17] (18) f00表示具有不同类标签的数据点被分到不同类别的数目,f11表示具有相同类标签的数据点被分到同一类别的数目,N表示数据样本总数。 本文实验取阻尼因子为0.8,迭代次maxits为1000,收敛迭代次数convits为50。选取的5个UCI测试数据集属性见表1。 表1 UCI测试数据集 本文算法(ZC-AP)与传统AP算法、M-AP算法作比较,以ACC、NMI、RI作为评价指标,结果见表2。图2是用表2数据绘制的准确率直方图,直观地展示3种算法在5个数据集上准确率ACC的比较。从表2和图2可看出,改进后的ZC-AP算法在5个数据集上的测试结果均优于原始AP算法和M-AP算法。以Twomoon数据集为例,原始AP算法的ACC、NMI、RI项指标分别为0.272、0.184、0.603,M-AP算法为0.728、0.184、0.603,而ZC-AP算法达到了0.997、0.969、0.993,ZC-AP比原始AP算法分别提高了3.67倍、5.27倍、1.65倍,比M-AP算法分别提高了1.37倍、5.27倍、1.65倍,说明改进算法在该数据集上的准确率有了较大提高,聚类结果与真实类标号吻合度较高。在German数据集上,ZC-AP算法比原AP算法在ACC、NMI、RI指标上分别提高了5.4%,34.5%和5.2%,比M-AP算法提高了7.7%、61.8%、5.2%。在Wpbc、Breast、Soybean等数据集上算法的准确率ACC均优于AP算法。 表2 聚类结果比较 图2 聚类结果直方图 为更直观观察ZC-AP聚类效果,我们从测试数据集中选择一个二维数据集Twomoon,将3种算法的聚类结果描绘在二维坐标轴上,如图3所示。由图3可看出,原始AP算法和M-AP算法虽然可将数据样本分为两类,但聚类准确率较低,而改进算法ZC-AP给出了正确的聚类结果。所以在对特征复杂数据样本进行聚类时,通过使用邻域相似度增大了同一簇点之间的相似程度,提高了聚类准确率。 图3 3种算法在Twomoon数据集上的聚类结果 在ZC-AP算法中,通过分析数据概率分布情况自动确定了邻域半径,而在人工选择邻域半径时,Eps需要在[0,50]之间随机选取,表3是以Wpbc数据集为例,展示人工选择邻域半径的聚类结果。由表3可看出:随机选取的Eps半径对聚类结果的影响很大,且聚类准确度均低于改进算法。例如,当Eps取0.258时,ACC为0.424,当Eps取10.821时,ACC为0.763,两者差别较大,由改进算法可以求得Eps为0.377,此时聚类精度达到0.818,NMI指标和RI指标也相应提升。因此改进算法较好地解决了邻域半径人工选取不当影响AP精度的问题。 ZC-AP算法需要拟合数据概率分布曲线,以Twomoon数据集为例,图4、表4、图5展示了拟合过程,此过程说明如下: 表3 人工选择Eps及相应准确率 图4 KNN 拟合函数SSER-SSER-SQUARE高斯拟合0.008 2510.98540.002 349多项式拟合0.006 2040.98920.002 039 图5 多项式拟合曲线 (1)计算Twomoon数据集的距离分布矩DISTn×n。 (2)对DISTn×n进行转置排序并绘图得到KNNn×(n-1)图,该图包含1502个样本点信息,由1502条曲线组成,排列较为密集,此处任取其中100条线显示其变化规律。 (3)KNNn×(n-1)图中各条曲线变化趋势大致相同,均在某点处急剧上升,其中K的取值范围为[1,1502],在该区间上K的取值对结果影响不大,可任意取值,为方便计算,取K=4反映其它曲线形状,绘制其概率分布图,分别进行多项式拟合和高斯拟合,比较拟合评价指标,发现高斯拟合精度高,但是拟合阶数也高,因此计算复杂度高。而在相同计算复杂度下,多项式拟合阶数较低,同时拟合精度较高,选择三阶多项式拟合和二次高斯拟合作比较,拟合结果见表4。 由表4可看出,三阶多项式拟合组内方差、均方根误差、相关系数这三项参数均优于二次高斯拟合,故选择多项式拟合求取Eps半径。多项式拟合效果如图5所示。 (4)对f(x)求二次导数可得f(x)″=12ax2+6bx+2c,求解二次导数方程的解为 (19) 舍去靠近边界的点,可得Eps=f(x0)。 (5)求以Eps为半径的邻域密度矩阵SRn。 (6)求邻域相似度矩阵STn。 (7)进行吸引度矩阵R和支持度矩阵A的计算和迭代更新。 本文提出一种基于邻域相似度的AP聚类算法,提高了传统AP算法在特征复杂数据集上的聚类精度,引入一种通过数据集相关统计特性自动确定邻域半径的方法,提高了算法的自适应性。在UCI数据集上与传统AP算法进行了聚类效果比较,验证了算法的可行性,得到以下结论: (1)采用邻域相似度作为新的聚类依据,取代原AP算法中的距离度量,能使算法在复杂数据集上的聚类精确度得到提高。 (2)采用统计学方法分析数据集的统计特性,根据数据概率分布自动求出邻域半径,提高了AP算法的自适应性。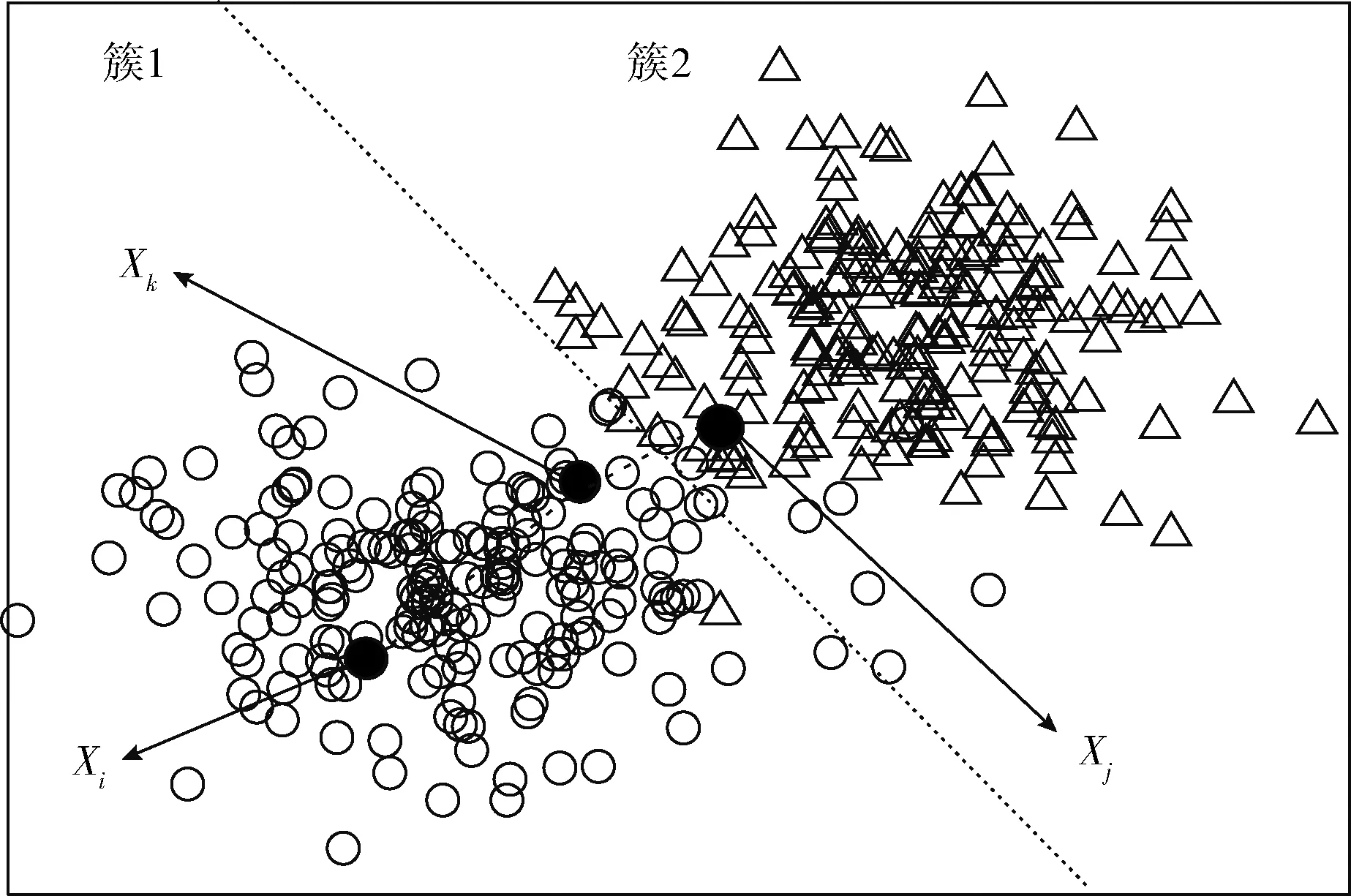
{(dist(N1,Yi)2 基于邻域相似度的近邻传播聚类算法
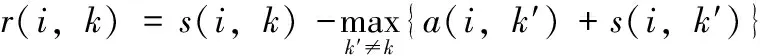
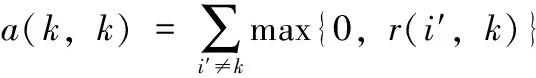
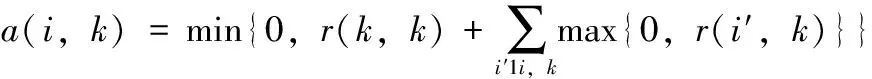
3 实验与分析

4 结束语

