通用特征基函数法结合MBPE计算目标宽带RCS

王仲根，唐晓菀，聂文艳

(1. 安徽理工大学电气与信息工程学院，安徽 淮南 232001；2.淮南师范学院机械与电气工程学院，安徽 淮南 232001)

矩量法(Method of Moments， MoM)[1]在计算目标宽带雷达散射截面(Radar Cross Section，RCS)时需要对频段内每个频率点逐一计算，计算效率低。随着一些高效方法的提出，如多层快速多极子法(Multilevel Fast Multipole Method，MLFMM)[2-3]以及特征基函数法(Characteristic Basis Function Method，CBFM)[4-6]的提出，有效地提高了单频率点的计算效率，但如果频段内需计算的频率点数多，将大大增加计算量，因此如何避免对每个频率点逐一计算是急需解决的一个难题。文献[7-8]提出应用阻抗插值技术以及最佳一致逼近技术减少阻抗矩阵的计算时间，但是这两种方法采用迭代法求解方程组，存在难以收敛的问题；文献[9-10]分别将渐近波形估计技术、最小二乘拟合与CBFM相结合计算目标宽带RCS，虽然上述两种方法有效地减少了所需计算的频率点数，但是每个采样点需重新计算特征基函数(Characteristic Basis Functions， CBFs)。文献[11-12]提出了一种通用特征基函数法(General Characteristic Basis Function Method， GCBFM)计算目标宽带RCS，该方法在待求频段的最高频率点构造与频率无关的通用特征基函数 (General Characteristic Basis Functions， GCBFs)，该GCBFs能够在待求频段内的每个频率点复用，节省了每个频率点计算CBFs的时间。

文献[13]提出了一种GCBFs自适应构造方法，减少了低频段的冗余计算，提高了计算效率；文献[14]应用奇异值分解技术(Singular Value Decomposition， SVD)对激励数目进行压缩，有效地减少了GCBFs数目，但是上述两种方法仍需重复计算每个频率点的阻抗矩阵以及缩减矩阵。

本文将GCBFM与模型参数估计技术(Model Based Parameter Estimation， MBPE)[15]相结合，通过计算少量采样频率点的RCS来获取目标整个宽频带RCS，该方法有效地解决了传统通用特征基函数法逐点计算RCS的难题，可应用于电大目标宽带RCS的计算。

1 通用特征基函数法

GCBFM将待分析目标剖分为M个子域，每个子域含有Ni个未知数(i=1，2，…，M)。在最高频率点fh，用多个方向的平面波激励照射每个子域，为每个子域构造主要特征基函数(PCBFs)。

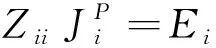
(1)

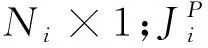
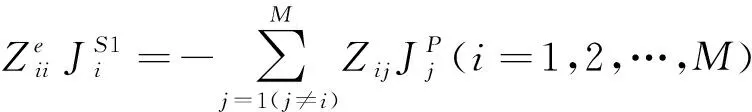
(2)

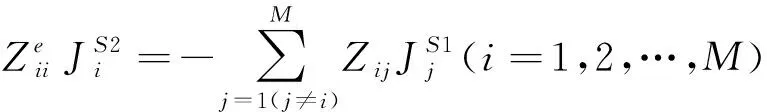
(3)

求解式(2)、(3)，即可得到各阶SCBFs。假设在θ和φ方向上各构造Nθ、Nφ个入射波激励，考虑2种激化方式，每个子域均可得到2NθNφ个PCBFs(JP)、2NθNφ个第一阶SCBFs(JS1)和2NθNφ个第二阶SCBFs(JS2)。应用SVD去除PCBFs以及各阶SCBFs中的冗余信息，即可得到每个子域的GCBFs。假设SVD后每个子域均得到K个GCBFs，则目标表面的电流可用GCBFs线性表示为

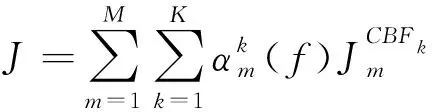
(4)

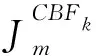
ZR(f)·α(f)=VR(f)

(5)

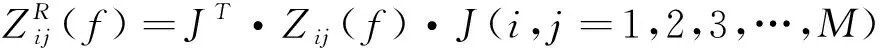
(6)

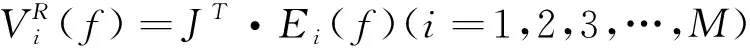
(7)

式中：α(f)为系数矩阵，直接求解式(5)并将α(f)代入式(4)，便可计算出目标在任意频率f处的表面电流。虽然GCBFs可以在待求频段内每个频率点复用，但当频率f变化时，ZR(f)需重新构造。从式(6)可以看出，ZR(f)构造过程中存在大量的矩阵向量积运算，对每个频率点重新构造缩减矩阵将不可取。本文将GCBFM与MBPE结合，通过计算少量插值频率点的RCS，快速获得整个频段的RCS，提高计算效率。

2 模型参数估计技术

根据有理函数插值法的基本原理，变量x的解析函数f(x)可以用一个有理分式表示。假设f(x)∈C[a，b]，则在区间[a，b]上，f(x)可表示成如下形式

(8)

式中：m、n分别为分子、分母的阶数，Dn(x)、Nm(x)均不可约，且Dn(x)≠0。f(x)中包含了m+n+2个参数，但自由度t只有m+n+1个，因此只需对f(x)进行t次采样，得到t组采样数据(xi，f(xi))(i=1，2，…，t)，便可得到f(x)的近似表达形式。

为得到有理分式f(x)的表达式，引入Thiele连分式[16]，假设第k次采样后，式(8)中分母Dn(x)和分子Nm(x)的表达式可通过下式确定

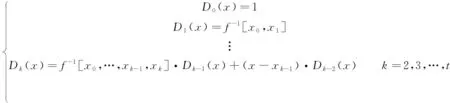
(9)

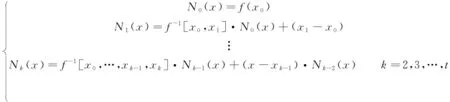
(10)

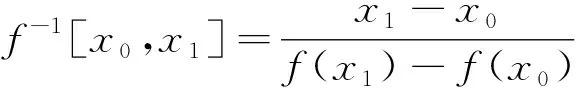
(11)

f-1[x0，x1，…，xi-1，x]=

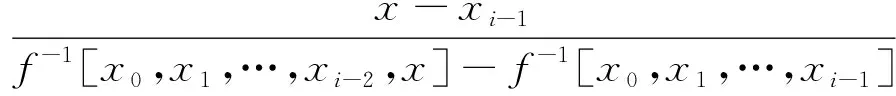
(12)

式中：i=1，2，…，k，通过k次采样后，得有理插值函数

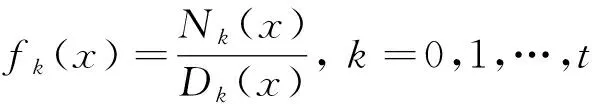
(13)

因此在待求频段[a，b]内，通过对采样点RCS的计算，即可得到待求频段内每个频率点的RCS，避免了对每个频率点缩减矩阵的重复构造，提高了计算效率。

3 数值算例与结果

为验证GCBFM-MBPE方法的有效性和精确性，分别对一个导体球以及一个导体组合体的宽带RCS进行了计算，SVD门限取0.001。

算例1：计算了一个半径为0.3m导体球在0.1～1GHz的宽带RCS，入射角θ=0°，φ=0°。在1GHz对目标进行剖分， 获得三角单元数2 346， 将其划分为8个子域， 未知数为5 250。 采用GCBFM， 在θ、φ方向上分别构造20个平面波激励，每个子域平均得到97个GCBFs，共778个GCBFs。分别应用商业软件FEKO、GCBFM以及GCBFM-MBPE计算了目标宽带RCS，计算结果如图1所示，GCBFM-MBPE的计算结果与与FEKO吻合较好，具有较高的计算精度。在GCBFM中，采样间隔为18MHz， 计算了51个频率点的RCS， 耗时33 469s。而采用GCBFM-MBPE只需计算24个频率点的RCS即可获得目标整个频段的RCS，耗时16 299s，与GCBFM相比计算效率提高了51%。

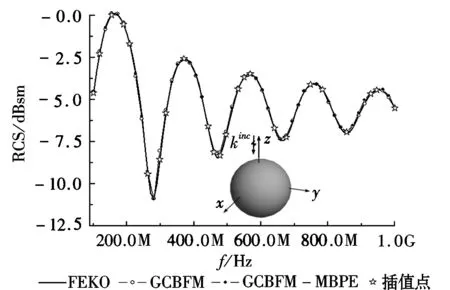
图1 导体球的宽带RCS

算例2：计算了一个导体组合体的宽带RCS，频率范围为0.1～3GHz，入射角θ=0°，φ=0°，组合体顶部边长为0.15m，疷部边长为0.075m，高为0.25m。应用FEKO软件对目标剖分，三角单元数为2 326，沿z轴方向将其划分6个子域，未知数为5 584，采用多激励入射共得到686个GCBFs。分别应用GCBFM、GCBFM-MBPE计算目标宽带RCS，两种方法计算结果如图2所示，GCBFM-MBPE的计算结果与GCBFM吻合较好。在应用GCBFM时，采样间隔为58MHz，计算了51个频率点的RCS，耗时38 732s；应用GCBFM-MBPE时，仅计算出22个采样频率点的RCS即可获得目标在整个频段的RCS，耗时18 204s，与GCBFM相比计算效率提高了53%。

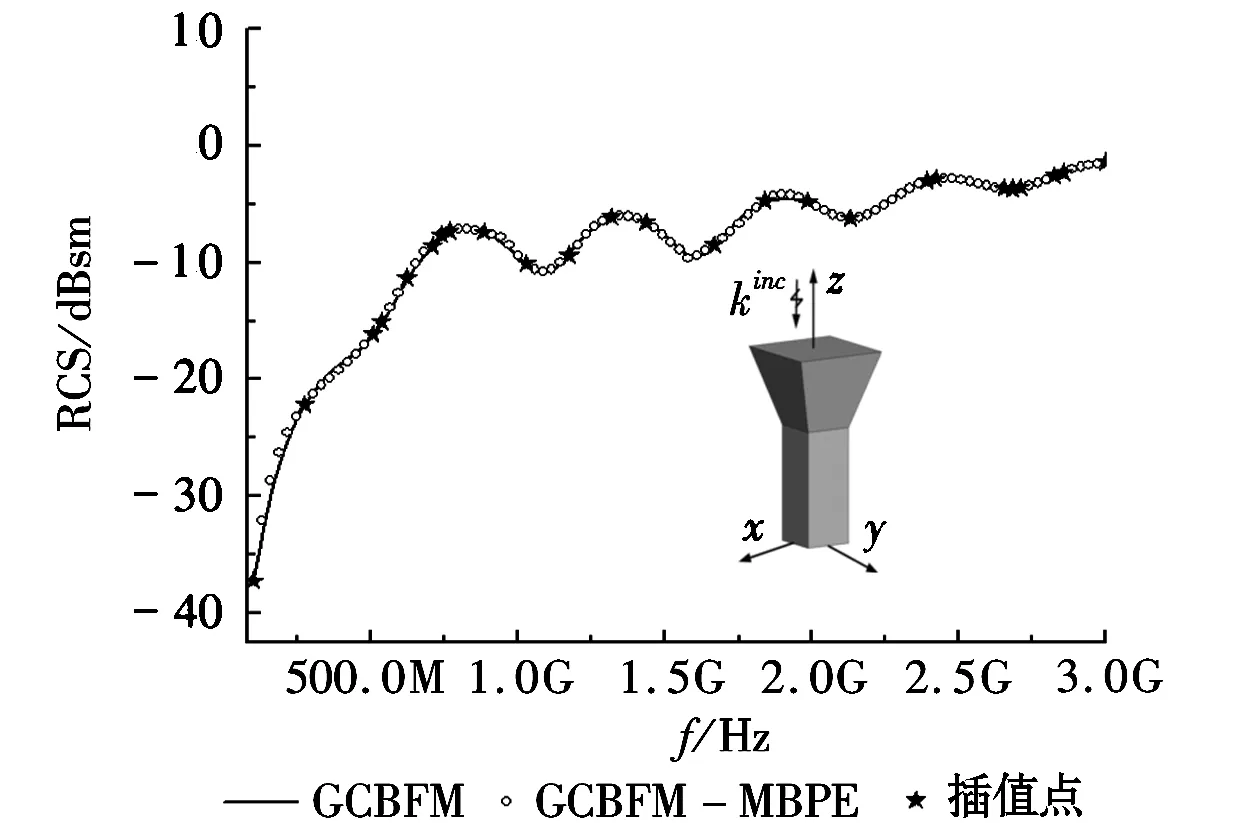
图2 组合体导体宽带RCS

4 结论

本文将GCBFM与MBPE相结合实现了导体目标宽带RCS的快速计算，该方法融合了GCBFM、MBPE两种方法的优点，即利用了GCBFM无需对每个插值频率点的CBFs重复计算的优点，又通过插值计算避免对每个频率点的阻抗矩阵以及缩减矩阵重复计算。算例验证结果表明，GCBFM-MBPE与传统GCBFM相比，计算效率得到了大幅度提高。