可扩展处理器中最大凸自定义指令迭代识别研究
王珊珊 刘万军 肖成龙
(辽宁工程技术大学软件学院 辽宁葫芦岛 125105) (celine.shanshan.wang@gmail.com)
可扩展处理器(专用指令集处理器)越来越多的被用到现代的电子设备中.例如Tensilica Xtensa[1],Argonaut RISC Core (ARC)[2],STMicroe-lectronic ST200[3],NIOS Ⅱ[4]等.可扩展处理器通过使用自定义功能单元(custom function unit, CFU)可以在灵活性和效率之间做出很好的折中.在CFU上执行的自定义指令封装了一组基本指令,并通过基本指令之间的并行化和链化来提高性能.通过对相同领域的不同应用程序使用相同的自定义指令集,可以使其具有一定的灵活性[5].此外,通过使用预验证的和预优化的基准处理器,可以减少设计复杂性和缩短产品上市时间[6].
为了满足成本约束,可扩展处理器经常在信号处理和图像处理等领域中使用.例如文献[7]提出了一种用于加速加密算法的自定义指令集的定制方法;文献[8]提出了一种专用于汽车应用领域传感器信号调理的可扩展处理器设计.可扩展处理器设计中涉及的最关键的问题之一是自定义指令识别问题.
近年来,自定义指令的自动识别成为嵌入式领域的研究热点之一.从程序的数据流图中人工识别一组最佳的自定义指令耗时且容易出错.因此,有必要构建完全自动化的自定义指令识别的编译流程.本文提出了一个用于识别最大自定义指令的最大凸自定义指令编译流程如图1所示.在设计流程中,应用程序源代码作为前端编译器generic compiler suite (GECOS)的输入[9].GECOS生成应用程序对应的控制数据流图(control data-flow graph, CDFG).CDFG是表示多个基本块之间的数据相关性的图.基于CDFG内的数据流图(data-flow graph, DFG),枚举出所有最大凸子图(最大凸自定义指令的图形化表示).然后,从所有枚举出的最大凸子图集合当中选择一组最佳的最大凸子图作为最终的自定义指令.每个选定的子图将聚合成1个虚拟节点.如果DFG仍然有未覆盖的有效节点,则继续执行1次迭代(包括枚举和选择).此过程持续到DFG中所有的有效节点均被覆盖.最后,将原始源代码转换为包含所识别的自定义指令的新源代码.
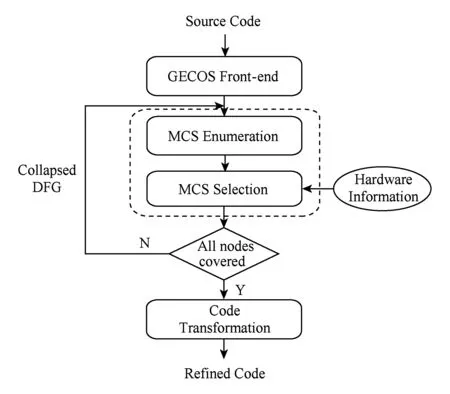
Fig. 1 Maximal convex custom instruction compilation flow图1 最大凸自定义指令编译流程
考虑到计算复杂性,之前的大多数研究仅枚举满足基准处理器的可用寄存器读写端口数目限制的自定义指令.此外,可以实现为硬件功能单元的自定义指令应该是凸的,否则不能原子地执行自定义指令.然而,通过使用内部状态寄存器,影子寄存器或Pozzi和Ienne[10]提出的技术,在大多数现有的可扩展处理器(诸如Tensilica Xtensa)中允许使用具有比寄存器读写端口更多的输入和输出操作数的自定义指令.此外,最近的一些研究表明枚举和选择最大自定义指令可以带来更多的性能提升[6,11].本文专注于最大凸自定义指令的自动识别.
本文的主要贡献有2个方面:
1) 提出了一种用于最大凸子图枚举的新算法.所提出的算法结合了自下而上的枚举方法和自上而下的枚举方法的优点.相比于文献[6,12]提出的算法,可实现数量级的加速.
2) 提出并实现了最大凸自定义指令迭代识别流程.在每次迭代中,采用高效的精确算法来选择最佳自定义指令集.与文献[6]中的方法相比,利用精确选择算法,在大多数情况下可以找到用于最大化提升性能的最佳自定义指令集.
1 相关工作
本节对自定义指令自动识别过程中涉及到的2个关键问题:自定义指令枚举和自定义指令选择,分别进行分析.
1) 自定义指令枚举.自定义指令枚举问题是从应用程序对应的数据流图中枚举出所有满足一定设计约束或用户约束的凸子图作为候选自定义指令.由于寄存器的读写端口的数目(IO)有限,例如 NIOS Ⅱ中的输入输出端口数一般为21,近期的一些研究主要是关注于枚举满足IO限制的子图.文献[13]首次证明了满足约束条件的子图(自定义指令的图形化表示)数目是多项式次的;Bonzini等人[14]提出了具有多项式时间的子图枚举算法;文献[15]使用约束编程解决子图枚举问题.然而,当应用程序对应的数据流图变大时,这些方法效率不高;文献[16]的作者首先提出了一种基于凸约束和IO约束下的二元决策树的枚举算法;Pozzi等人[17]通过添加基于永久输入数量的修剪标准进一步改进了该算法;文献[18]中提出的算法使用预过滤方法,在保留文献[16]中算法所有优点的同时,可以进一步修剪大量搜索空间;文献[19]在此前的研究基础上,提出了基于并行计算的子图枚举算法,实验结果表明相对于串行算法,并行算法可达到近似线性的加速比;Yu和Mitra[20]通过枚举向上的锥体型子图和向下的锥体型子图构建连通子图,然而,在这个算法中,同一子图可能被枚举多次.
此前的研究表明:放松输入约束和输出约束可以带来更好的性能提升[11,21].例如文献[21]的实验显示IO数目为21的约束下,识别自定义指令可以将DES加密算法的执行时间计数减少到67%,而完全放松IO约束的情况下算法的执行时间减少到56%.因此,在没有IO约束的条件下识别自定义指令近年来已经受到越来越多的关注.通过使用内部状态寄存器和影子寄存器,自定义指令枚举问题可以被转换为最大凸子图(maximal convex subgraph, MCS)枚举问题.Pothineni 等人[22]首次提出了MCS枚举算法,该算法基于不兼容性图枚举MCSs,然而,该算法仅生成连通MCS.文献[11]将等价节点分组并构建集群图,MCS枚举问题被转换为最大团枚举问题.Atasu 等人[6]首次证明了MCS数目上限是2|VI|,其中|VI|是DFG中的无效节点集合.文献[12] 按照自顶向下的方式通过对DFG进行分割来枚举MCS.然而,此方法不能保证所枚举的子图是唯一的和最大的.
上述研究都是以自底向上方式或自顶向下的方式来枚举MCS.自底向上方式可以通过聚合等价节点来减小DFG的大小;自顶向下的方式可以通过将DFG分解成更小的图来减小DFG的大小.为了结合自底向上方式和自顶向下方式的优点,本文提出了先自底向上聚合后自顶向下分割的方法来高效地枚举MCS(夹心方法).本文还给出并证明了在给定DFG中MCS的数量上限.
2) 自定义指令选择.在自定义指令枚举步骤之后,自定义指令选择步骤确定哪些枚举的子图应当作为最终的自定义指令,并在硬件中实现.一般来说,在自定义指令选择期间应该考虑的因素包括运行时性能(时钟周期计数)、面积成本、功耗和代码量[23].一些先前的研究旨在选择定制指令以在满足给定面积约束的同时实现最佳性能提升[6,24-25].一些其他工作尝试选择考虑功耗约束的自定义指令[26].这些研究通常在上述因素之间进行权衡.在本文中,自定义指令选择步骤关注于性能提升的最大化.没有其他因素的限制,可以实现最佳的性能提升.文献[6]使用一个价值函数贪婪地选择自定义指令.然而,实验显示候选子图的数量通常很少,而且很多候选子图之间存在覆盖关系.通过非覆盖约束条件,可以大量地修剪搜索空间.因此,采用精确算法可以保证性能提升的最大化.
2 相关定义
数据流图是一种有向无环图.它是一个图G=(V,E),其中顶点集v={v1,v2,…,vn}表示基本指令,边集E={e1,e2,…,em}∈V×V表示指令之间数据依赖关系.
定义1. 无效节点.由于体系结构的限制,内存操作和分支操作等基本指令不能包含在自定义指令中,代表这些基本指令的节点被视为无效节点.
子集VI⊆V表示G中的无效节点.子集V-VI表示G中的有效节点.枚举的最大凸子图是仅包含有效节点的图.
定义2. 凸子图.对于G的子图S,∀u,v∈Vs,若在G中u与v之间的任何路径都只经过S中的节点,则称S是G的凸子图.
可以实现为硬件功能单元的自定义指令应该是凸的,否则不能原子地执行自定义指令.数据流图中的凸子图如图2阴影部分所示.子图{n1,n2,n3}是一个凸子图,而子图{n1,n2,n4}是一个非凸子图.
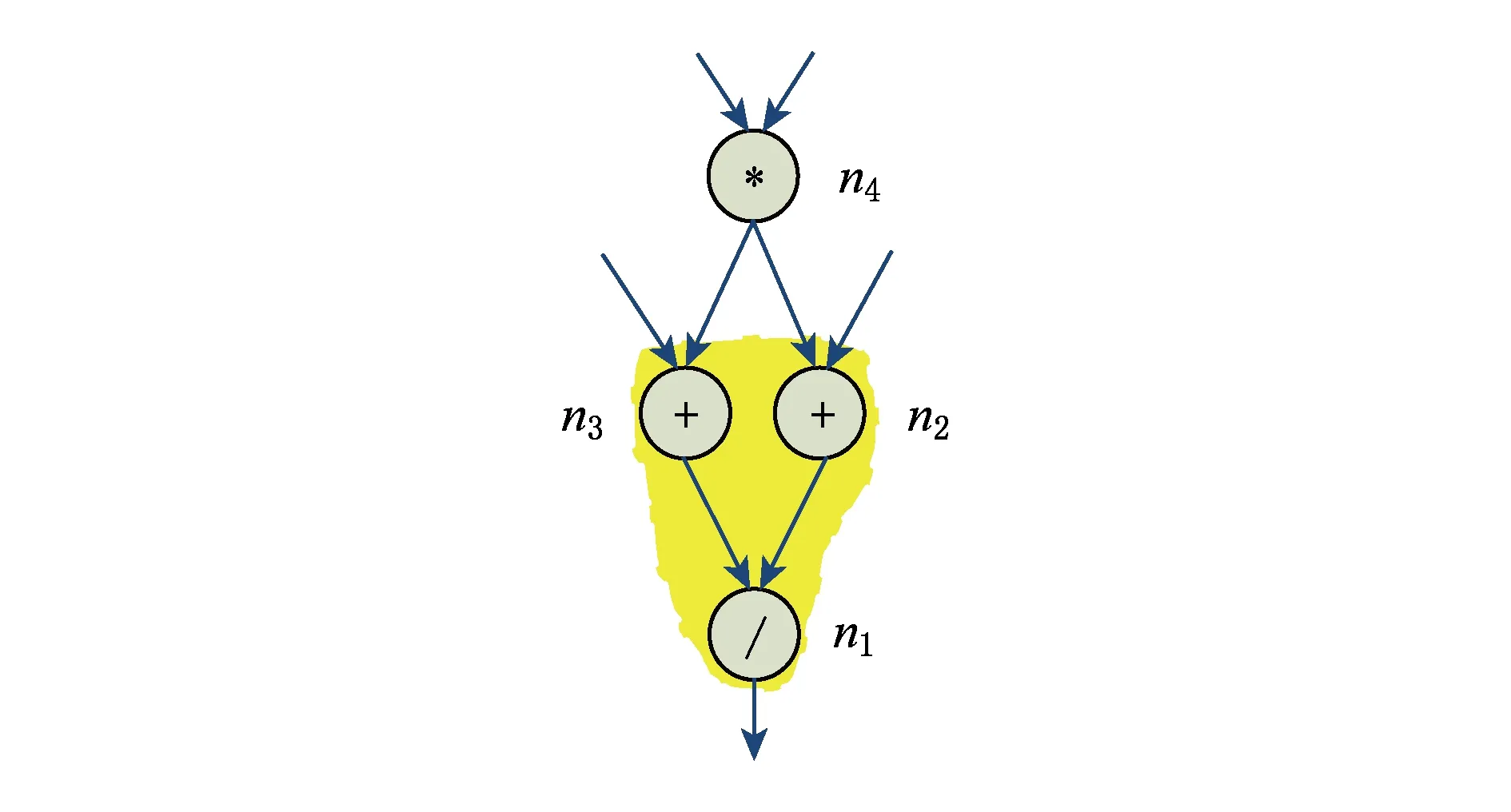
Fig. 2 A data flow graph with a convex subgraph图2 数据流图中的凸子图
定义3. 最大凸子图.G中凸子图S,其不包含无效节点,且不能通过添加VVI中的任一节点形成更大的凸子图,则称S为最大凸子图.
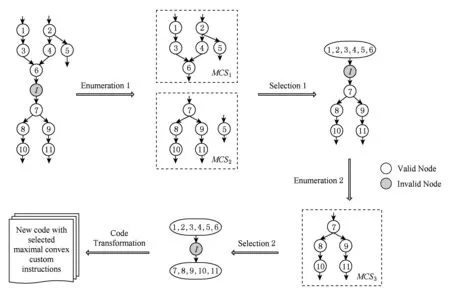
Fig. 3 An example using the iterative design flow图3 迭代设计流程示例
MCS识别包括2个基本步骤: MCS枚举和MCS选择.MCS枚举问题是找到给定DFG中的所有MCS;MCS选择问题是从枚举的MCS中选择最佳的非重叠的MCS子集.2个候选MCS可能有共同的节点.允许自定义指令间存在节点重叠,有时可以提升性能,但它也不必要地增加功耗并且使得代码转换变得非常困难.类似于文献[6]中提出的方法,本文不允许任何MCS之间存在节点重叠.迭代设计流程示例如图3所示.在第1次迭代步骤中枚举出了2个MCS即MCS1和MCS2.由于这2个MCS具有共同的节点5,根据非重叠的规则,只能选择MCS1或MCS2.
给定DFGG=(V,E)和节点u,G中的节点与u的关系可以定义:
1) 节点u的直接前驱节点集.IPred(G,u)={v|v∈V,(v,u)∈E}.
2) 节点u的直接后续节点集.ISucc(G,u)={v|v∈V,(u,v)∈E}.
3) 节点u的所有前驱节点集.Pred(G,u)={v∪Pred(G,v)|v∈IPred(G,u)}.
4) 节点u的所有后继节点集.Succ(G,u)={v∪Succ(G,v)|v∈ISucc(G,u)}.
5) 节点u的分离节点集.Disc(G,u)=G-Pred(G,u)-Succ(G,u)-u.
无效节点集可以进一步分为2组.
定义4. 边界无效节点.无效节点u是G的边界无效节点,当且仅当Pred(G,u)∩{VVI}=∅或Succ(G,u)∩{VVI}=∅.
定义5. 内部无效节点.无效节点u是G的内部无效节点,当且仅当Pred(G,u)∩{VVI}≠∅ 和Succ(G,u)∩{VVI}≠∅.
3 最大凸自定义指令迭代识别算法
图3给出了从给定应用程序的数据流图中识别MCS的过程示例.数据流图由12个节点组成,包括11个有效节点和1个无效节点(节点I).MCS识别流程以迭代方式进行.在第1次迭代中,在MCS枚举步骤枚举出2个MCS即MCS1和MCS2.然后,根据非重叠规则,MCS选择步骤仅选择其中一个MCS(例如MCS1)作为自定义指令.MCS1内的节点聚合到虚拟节点中,聚合之后生成的DFG作为第2次迭代的输入.在第2次迭代中,选择MCS3作为自定义指令.到目前为止,原始DFG中的所有有效节点都被覆盖了.最后,源程序被转换为包含了所识别的自定义指令的新代码.
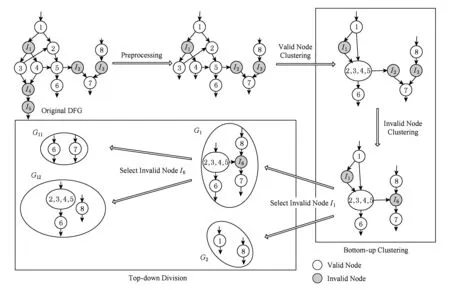
Fig. 4 Summary of our approach to maximal convex subgraph enumeration图4 最大凸子图枚举方法示例
最大凸自定义指令的迭代识别流程的伪代码如算法1所示.算法1接受DFG作为输入,并产生一组选定的最大凸子图作为输出.在每次迭代中,算法1首先调用最大凸子图枚举算法(行③);然后,根据候选子图的性能增益来选择非重叠的MCS作为自定义指令(行④~⑤).迭代结束的条件为原始DFG中所有有效节点均被自定义指令覆盖.
算法1. 最大凸自定义指令迭代识别.
输入:数据流图G(V,E);
输出:最佳最大凸自定义指令集.
①IterativeIdentification(GraphG);
② whileG包含有效节点do
③MCS=MCSEnumeration(G);
④ 按照性能增益对MCS中的最大凸子图排序;
⑤ 选择最佳的非重叠最大凸子图子集;
⑥ 在图G中将选择的每个最大凸子图聚合成单个节点;
⑦ end while
4 最大凸自定义指令枚举算法
本节提出了一种结合自下而上方法和自顶向下方法的夹心枚举算法.该算法首先删除边界无效节点;然后,通过自下而上的方式聚合节点;最后,采用自上而下的分割方法将DFG分割成更小的图,最终生成所有最大凸子图.最大凸子图枚举方法示例如图4所示:
4.1 预处理
根据定义,边界无效节点在VVI没有前导,或者在VVI中没有后继.因此,可以将边界无效节点DFG中移除而不会影响最大凸子图枚举的结果.例如在图4中,从DFG中移除边界无效节点I4和I5不会影响最大凸子图的枚举结果.在实际的应用程序对应的数据流图中存在着大量无效节点.移除所有边界无效节点的预处理可以最大地减少DFG中的无效节点数目,进而减少自顶向下分割步骤中涉及的递归次数.
4.2 自下而上聚合
1) 有效节点聚合.如果2个有效节点u和v满足Pred(G,u)∩VI=Pred(G,v)∩VI和Succ(G,u)∩VI=Succ(G,v)∩VI,则将节点u和节点v聚合成1个节点.通过有效节点聚合在保证最大凸子图的枚举结果不受影响的同时,可以大大减少DFG中的有效节点数目,从而减少枚举算法的运行时间.
2) 内部无效节点聚合.由于在预处理步骤中删除了所有边界无效节点,可以通过聚合内部无效节点进一步减小DFG中的无效节点数目和减少自顶向下分割过程中涉及的递归次数.G中的2个内部无效节点u和v,如果这2个节点满足以下3个条件之一,则u和v可以聚集到1个节点中,而不影响最大凸子图枚举的结果:
①Pred(G,u)∩{VVI}=Pred(G,v)∩{VVI};
②Succ(G,u)∩{VVI}=Succ(G,v)∩{VVI};
③Pred(G,u)⊆Pred(G,v)且Succ(G,u)⊆Succ(G,v).
内部无效节点聚合的示例如图4所示.内部无效节点I2和节点I3满足条件:
Succ(G,I2)∩{VVI}=Succ(G,I3)∩{VVI},
I2和I3可以聚合成1个无效节点I6.本文的内部无效节点的聚合方法和文献[6]的主要区别是:本文不仅聚集在VVI中具有相同后继集合或相同前驱集合的内部无效节点(条件①,②),而且满足第3个条件的2个节点也可以聚合成1个节点.而文献[6]中的方法只能聚合满足条件①,②之一的内部无效节点.图5中,使用本文提出的内部无效节点聚合方法,无效节点I1和无效节点I2满足Pred(G,I2)⊆Pred(G,I1)且Succ(G,I2)⊆Succ(G,I1),2个节点可以聚集成1个节点I.但是,文献[6]提出的聚合方法无法集合这2个节点.
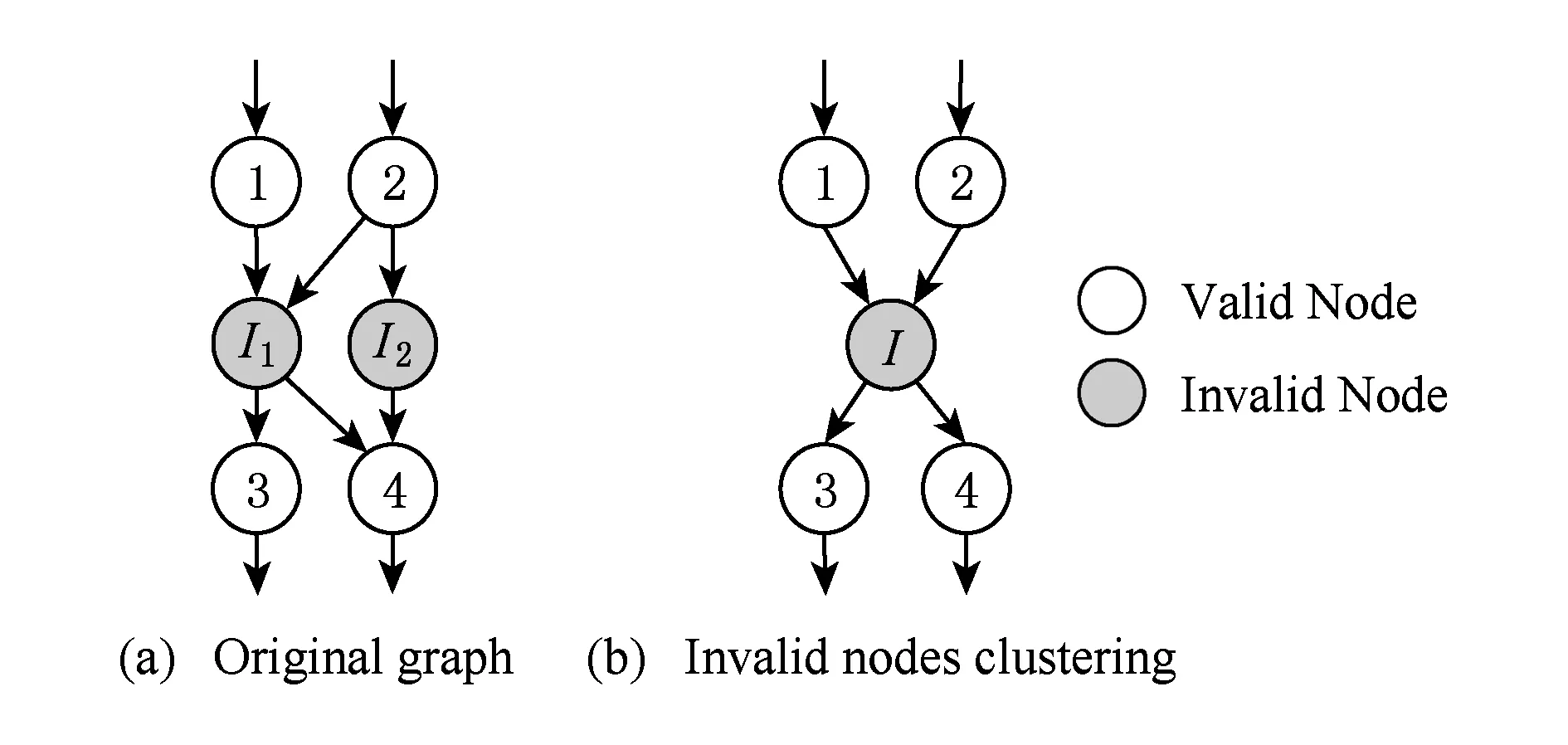
Fig. 5 Invalid nodes clustering图5 无效节点聚合
4.3 自顶向下分割
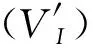
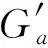
(1)
例如图4中,在预处理和自底向上聚合之后生成了一个由5个有效节点和2个无效节点(I1和I6)组成的图.首先选择无效节点I1作为分割点,根据式(1)导出2个新的子图G1和G2;然后,选择无效节点I6作为分割点,G1进一步分成2个子图(G11和G12).由于G11和G12中没有无效节点,因此G11和G12即为MCS.
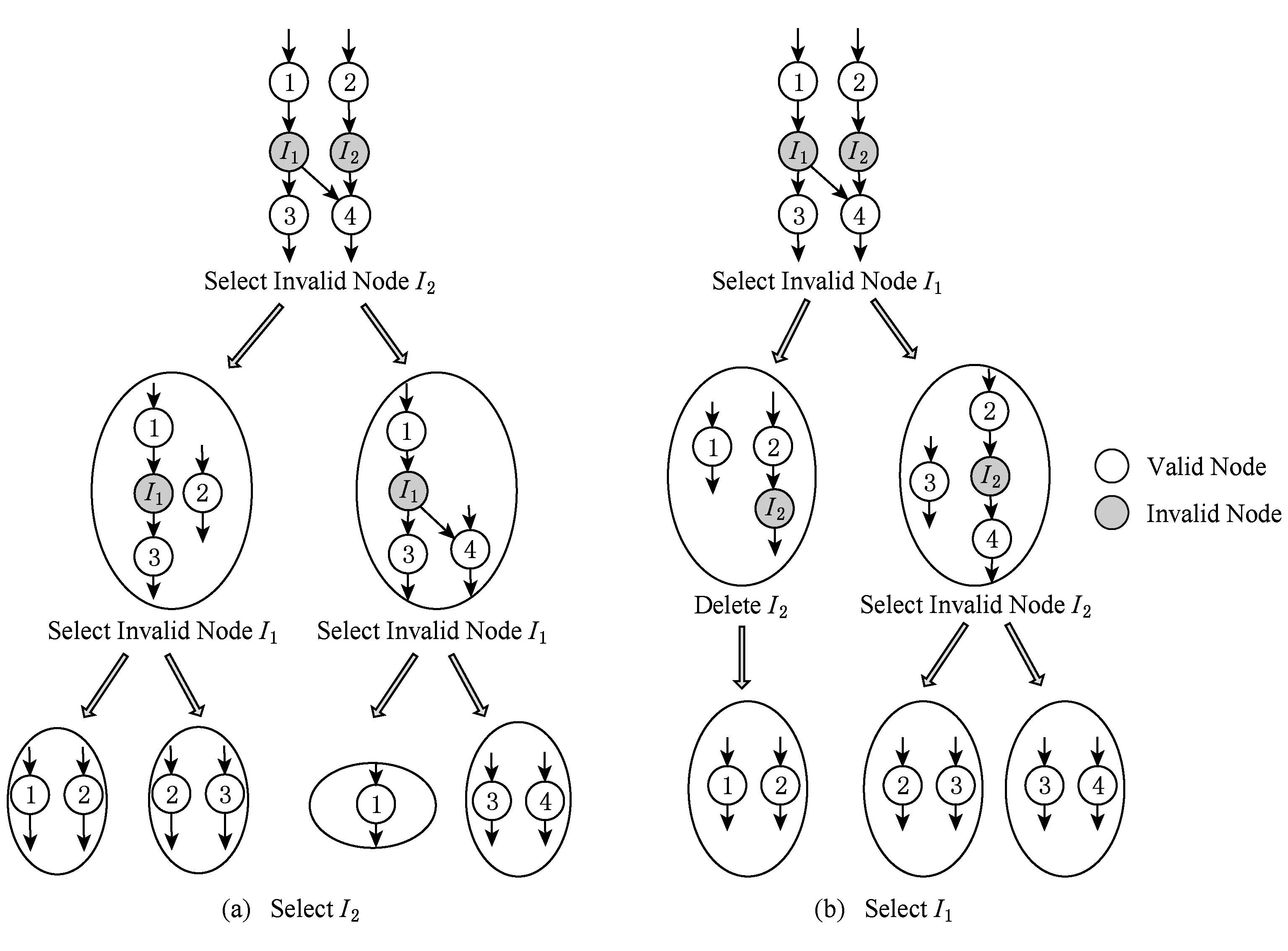
Fig. 6 Selection of invalid nodes for division operations图6 无效节点的选择对分割操作的影响
然而,选择哪个无效节点作为分割点对算法运行效率起关键作用.无效节点的选择对分割操作的影响如图6所示.在图6(a)中,首先选择无效节点I2进行分割,最终得到4个子图,其中子图{1}并非最大凸子图.在这种情况下,需要检查子图是否为最大凸子图,这样会额外增加算法的运行时间.然而,如果首先选择无效节点I1进行分割,则所有生成的凸子图都是最大凸子图,如图6(b)所示.这样不需要额外地检查来判断生成的子图是否为最大凸子图.观察发现,这是因为无效节点I1具有私有前驱和私有后继,而无效节点I2不具有私有后继.(无效节点的直接前驱或直接后继称为u的私有前驱或u的私有后继,当且仅当它是有效节点,并且不是任何其他无效节点的前驱或后继).
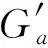
定理1. 给定1个无效的节点u,u至少有1个私有前驱或至少1个私有后继,那么在Disc(Gcur,u)中没有MCS.
证明. 假设在Disc(Gcur,u)中有1个MCS为m.如果u有1个私有前驱v,那么v不是任何其他无效节点的前驱.此外,v不能是Disc(Gcur,u)中任何无效节点的后继.因此,v可以添加到m以形成更大的最大凸子图.这与假设m是最大凸子图矛盾.
证毕.
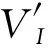
算法2. 最大凸子图枚举算法.
输入:数据流图G(V,E)、无效节点集VI;
输出:最大凸子图集.
①MCSEnumeration(GraphG);
②CHECK=False;
③ 预处理: 移除边界无效节点;
④ 聚合: 有效节点聚合及无效节点聚合;
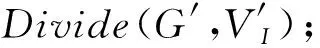
⑥ ifCHECK=True then
⑦ 进行最大化检查和冗余检查;
⑧ end if
⑨Divide(GraphG,InvalidNodeSetVI);
⑩ ifG=∅
基于本文的分割算法,可以得到给定DFG中的MCS数量的上限由定理2确定.
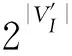
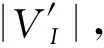
证毕.
本文提出自下而上的聚合方法产生的无效节点的数目通常小于通过在文献[6]中提出的聚合方法.因此,MCS数量的上限比文献[6]中给出的上限更小.
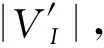
5 自定义指令选择
在自定义指令枚举步骤之后,现在的任务是从所有枚举出的最大凸子图当中选择最佳的子集作为最终的自定义指令.由于本文的目标是最大化提升性能,所以使用性能增益评估每个候选最大凸自定义指令.每个自定义指令S的性能增益P(S)可定义为该自定义指令S的硬件实现相比于用软件实现的性能提升(以时钟数表示),即:
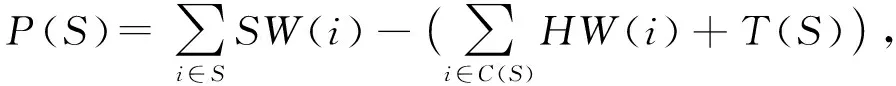
(2)
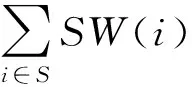
在文献[6]中,作者提出了一个价值函数来判定候选自定义指令的优先等级,以便在每次迭代中贪婪地选择等级高的MCS作为最终的自定义指令.然而,实验中发现枚举出的候选MCS的数量通常非常小.此外,通过应用非重叠规则,可以大大减少搜索空间.因此,采用精确算法来选择自定义指令可以保证最大化提升性能.
首先根据MCS之间的重叠关系,构建出兼容图.此兼容图为无向图,其中每个节点对应于由枚举步骤生成的MCS.如果2个MCS——MCSi和MCSj——不存在共同的节点,则在MCSi和MCSj对应的2个节点之间建立1条边.每个节点分配有相应MCS的性能增益.因此,自定义指令选择问题被转换为典型的带权最大团问题.带权最大团问题的最大团对应于自定义指令选择问题的最佳子集.一个具有5个节点的兼容图的示例如图7所示.每个节点被赋予权重(或性能增益).此示例的最大团是{MCS1,MCS2,MCS5}.
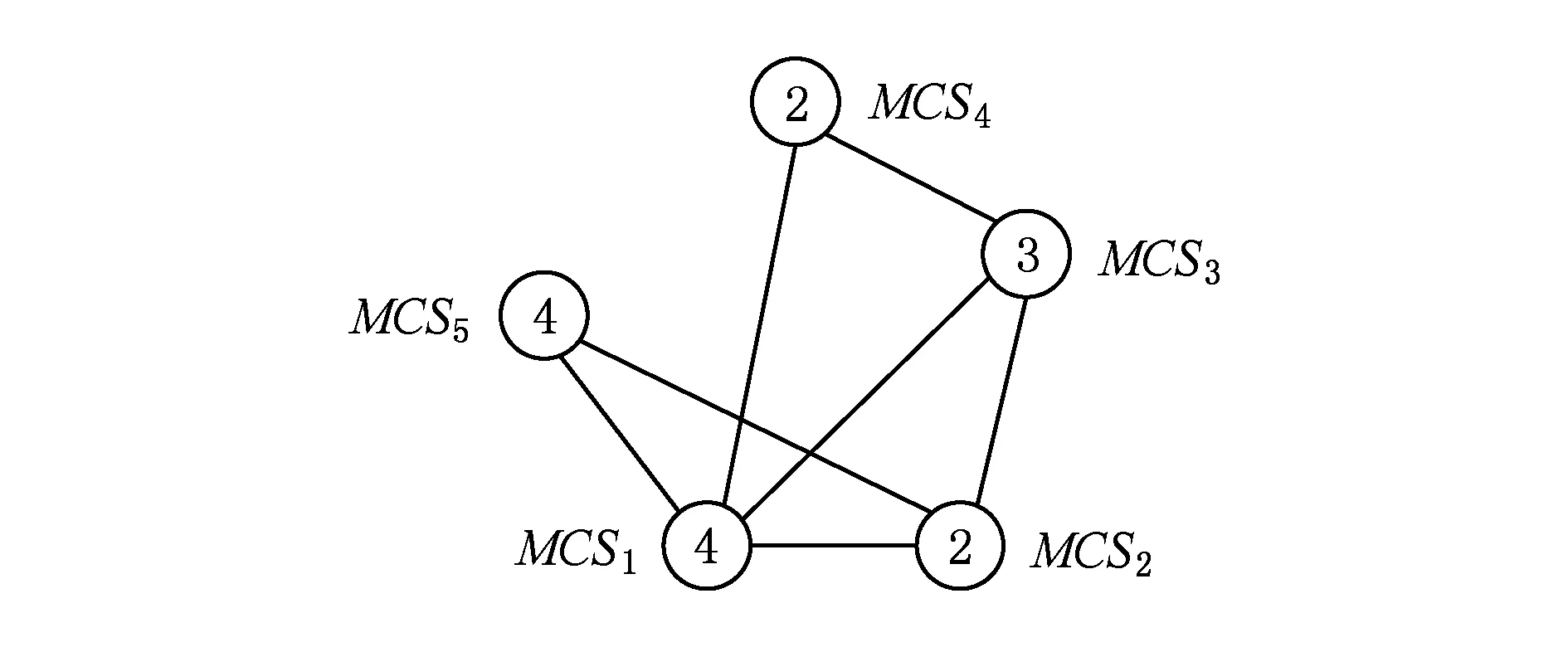
Fig. 7 An example of building compatibility graph图7 兼容图构建示例
在构建兼容图之后,使用分支定界的方式寻找最大团.在该算法中,所有候选MCS根据性能增益以降序排序.算法在分支定界搜索之前首先用贪婪算法生成一个解决方案.一方面,贪婪解决方案提供了一个很好的下限,可以在分支定界过程中快速修剪搜索空间;另一方面,获得的贪婪解决方案可以保证如果算法运行太长时间,则至少获得不劣于贪婪的解决方案.在搜索过程中,如果当前解决方案比目前为止的最佳解决方案好,则更新下限.
6 实验与结果分析
本实验的环境为 i3-3240 3.4 GHz处理器、4 GB主存储器、操作系统为Windows 8.测试基准集来源于MediaBench[27]和MiBench[28],这些基准是由通用编译平台GECOS[8]进行前端编译和模拟的.实验中使用的数据流图特征如表1所示:
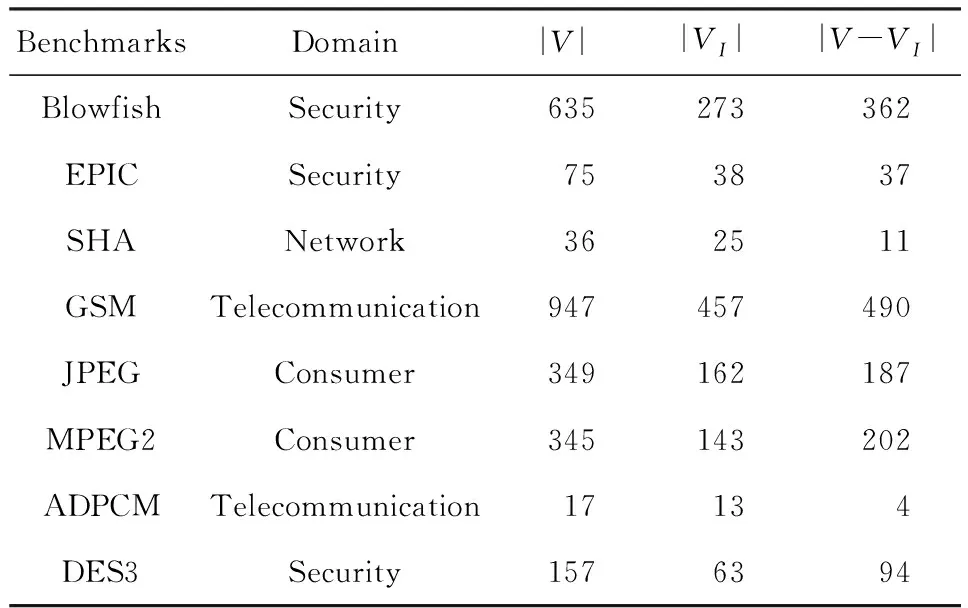
Table 1 Characteristics of the Data Flow Graphs of
列|V|、列|VI|和列|V-VI|分别表示数据流图中节点的数目、无效节点的数目和有效节点的数数目.实验主要分为2个部分:自定义指令枚举算法运行时间的比较和自定义指令对性能提升的比较.
6.1 预处理和聚合结果比较
在实验中,首先本文提出的自下而上聚合方法与在文献[6]中提出的聚合方法进行比较.为了详细比较聚合方法的效果,本实验分别评估有效节点和无效节点聚合之后的数量变化.2种聚合方法的结果见如表2所示.
由于本文中的预处理和有效节点聚合与文献[6]中的方法相同,通过预处理和有效节点聚合,2个方法获得的结果是相同的(列Preprocessing和列Valid Nodes Clustering).从表2可以看出,在预处理和有效节点聚合之后,无效节点的数量和有效节点的数量极大地减少.还可以观察到,本文提出的无效节点聚合方法优于文献[6]中的无效节点聚合方法.对于测试基准程序Blowfish,JPEG,DES3,本文的聚合方法将无效节点的数量分别减少到49,8,16,而文献[6]中的方法只能将无效节点的数量减少到53,10,19.
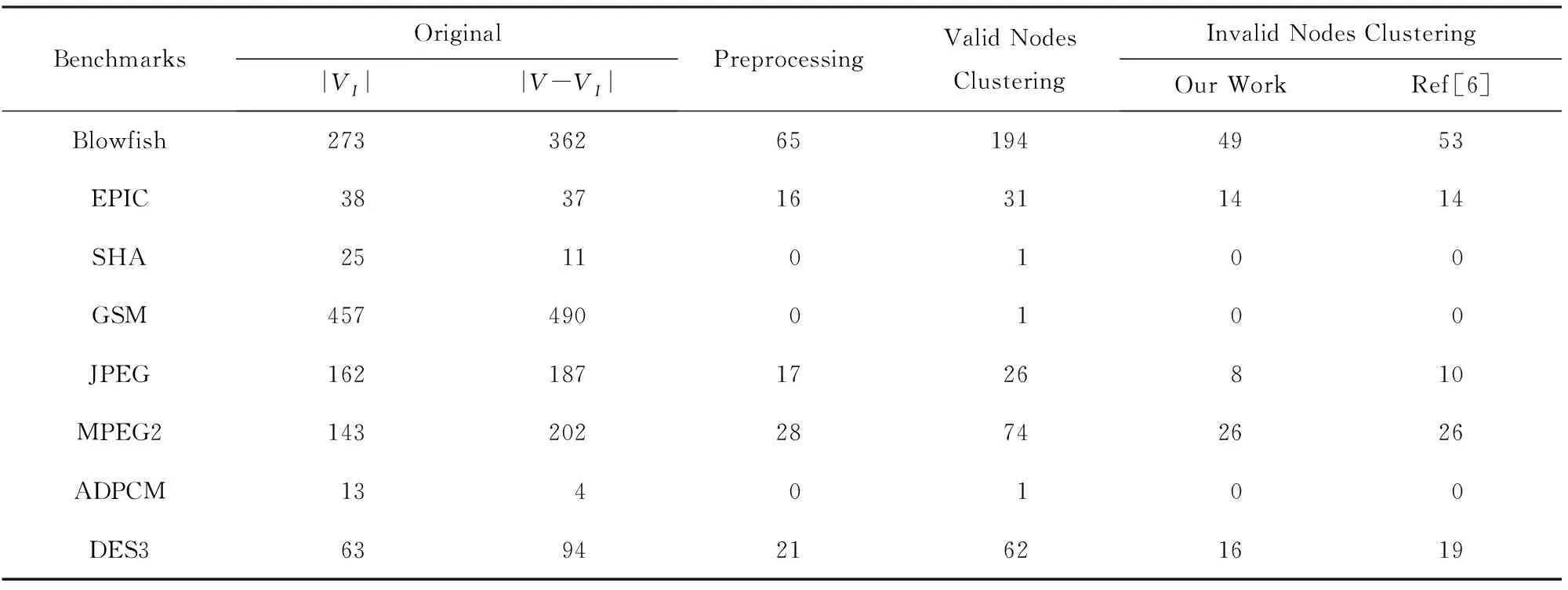
Table 2 Preprocessing and Clustering Results表2 预处理和聚合结果比较
6.2 最大凸自定义指令枚举算法运行时间比较
为了评估所提出的枚举算法的运行时间,将本文提出的最大凸子图枚举算法(表示为MS)与文献[12]中的自顶向下枚举算法(表示为TD)和文献[6]中的自底向上算法(表示为ILP)进行了比较.为了比较的公平性,所有相关的算法在相同的开发环境中实现,并且使用相同的数据结构表示MCS.
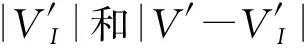
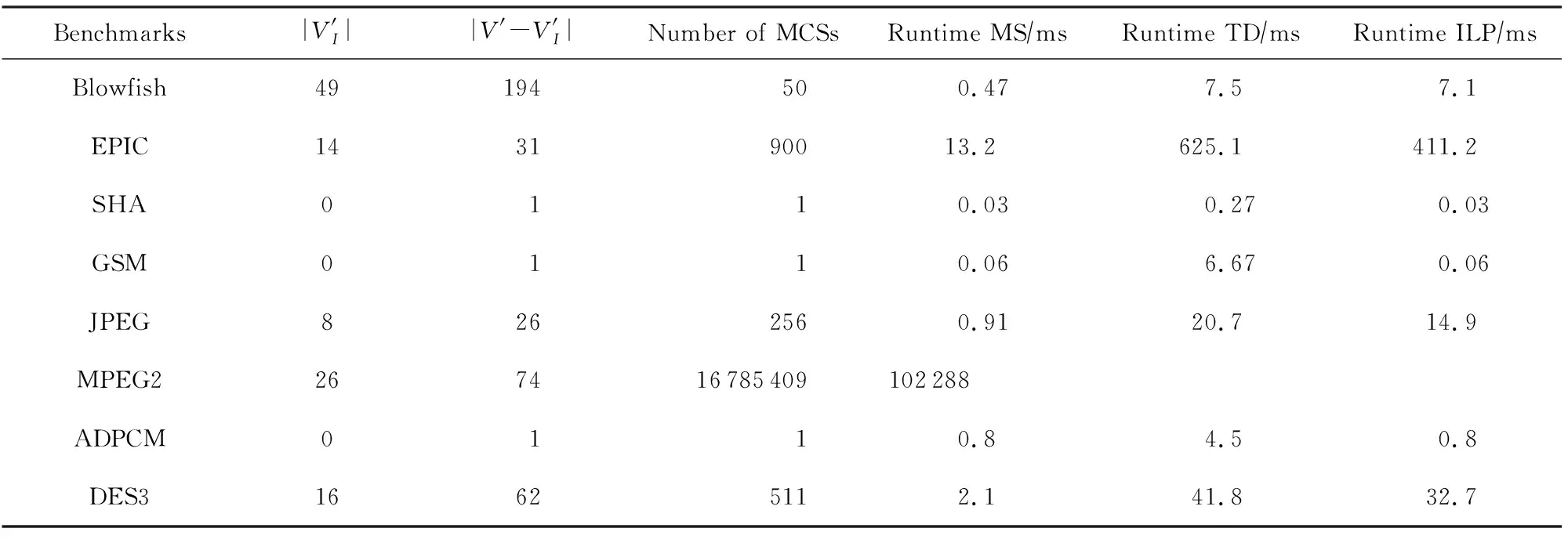
Table 3 Comparison of MCS Enumeration Algorithms表3 MCS枚举算法运行时间比较
实验结果表明:本文提出的算法MS显著快于算法TD和算法ILP.可以观察到:对于包含少于100个无效节点的测试基准程序,相比于自顶向下的算法TD,本文的算法可以达到5.6~47.3倍的加速.对于具有超过100个无效节点的测试基准程序,算法MS相对于算法TD的加速更加显著,为15.9~111倍.对于测试基准程序MPEG2,算法MS需要102 s产生超过1 600万个MCS,而算法TD无法在10 h内产生结果.由于算法TD无法在合理的实间内产生所有的结果,在算法TD中添加了一个计时器(时间设为102 s).当计时器设定的时间结束时,算法TD停止枚举.实验中观察到算法TD枚举的子图数量约为1 400万.在这些枚举的子图中,存在大量的子图是冗余的或非最大的.此外,从算法MS枚举的MCS中选择定制指令之后,对测试基准程序的性能提升是2.85倍.而从算法TD枚举的子图中选择自定义指令所达到的性能提升只有2.4倍.
相比于算法TD,算法MS的运行时间的减少主要有3个原因:
1) 通过预处理和无效节点聚合之后可以去除相当多数量的无效节点,使得二叉查找树的搜索空间大量减少.例如对于测试基准程序Blowfish和GSM,在预处理和无效节点聚合之后,无效节点的数量分别减少为49和0.
2) 有效节点聚合可以减小DFG的大小,这有助于减少诸如式(1)中的计算时间.例如对于测试基准程序JPEG,通过有效节点聚合之后,有效节点的数量从187减少到26.
3) 选择具有私有前驱和私有后继的无效节点可以避免产生冗余或非最大凸子图.如图6(a)所示,根据算法TD中提出的无效节点选择策略,其首先选择无效节点I2来分割图.在这种情况下,枚举出非最大子图{1},导致额外的搜索空间.此外,需要执行最大化检查以过滤掉非最大子图,这也极大地增加了算法的运行时间.相反,本文提出的枚举算法选择无效节点I1来分割图.所有枚举出的子图都是唯一的最大凸子图.
实验结果显示,对于测试基准程序SHA,GSM和ADPCM,算法MS运行时间和算法ILP的运行时间相当.分析发现测试基准程序SHA,GSM和ADPCM中的无效节点均为边界无效节点,经过预处理(算法MS和算法ILP的预处理相同),无效节点的数目为零,因此预处理之后的图为唯一的MCS.所以算法MS运行时间和算法ILP的运行时间一样.然而,对于测试基准程序DES3,JPEG,EPIC,算法MS相对于算法ILP的加速比分别为15.6倍,16.4倍,31.2倍.
相比于算法ILP,算法MS的运行时间的减少主要有2个原因:
1) 算法ILP不能保证枚举的凸子图是最大的,并且可能多次生成相同的子图.在这种情况下,需要额外的最大性检查和冗余校验来获得MCS,而最大化检查和冗余校验非常耗时.算法MS总是优先选择具有私有前驱和私有后继的无效节点进行分割,这样可以避免生成冗余MCS.只有当没有具有私有前驱和私有后继的无效节点作为分割点时,才需要执行冗余检查和最大化检查.
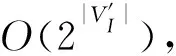
6.3 性能提升
本节将所提出的自定义指令选择方法所实现的性能提升与文献[6]中提出的启发式选择方法实现的性能提升进行比较.
在实验中,比照文献[29-30],假定基准处理器是单发射流水线结构的处理器.乘法指令的软件时延为2个周期,其余指令的软件时延均为1个周期.自定义功能单元中实现的基本指令的硬件延迟信息如表4所示:
Table4HardwareTimingoftheOperationsImplementedintheCustomFunctionUnits

表4 自定义功能单元中指令的硬件延迟信息
假定包含多个节点的自定义指令在自定义功能单元上执行,而应用程序中未被包含进自定义指令的基本指令在基准处理器上执行.给出了使用自定义指令应用程序总时延的计算:
(3)
其中,HW(i)表示自定义指令i的硬件延迟;T(S)表示传输自定义指令的输入和输出操作数所需的额外时延.式(3)等号右边的第1项表示所选自定义指令累积硬件时延的总和(SC表示所选自定义指令的集合,C(S)表示是位于所选自定义指令S的关键路径上的节点);式(3)等号右边第2项表示未包含进自定义指令的基本指令的累积软件时延(PI表示未包含的基本指令的集合).
通过使用最大凸自定义指令实现性能提升的计算:
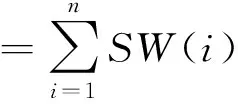
(4)
其中,式(4)等号右边是原始应用程序的源代码中所有基本指令的累积软件时延(n表示原始代码中基本指令的数量).
精确选择算法和启发式选择算法[6]所获得的性能提升的对比,如图8所示.在实验中,假设核心寄存器有2个输入端口和1个输出端口.使用式(4)计算相应的性能提升,可以观察到本文提出的方法优于文献[6]中提出的方法.例如对于测试基准程序DES3,本文方法实现的性能提升是5.8倍,而使用文献[6]中的方法实现的性能提升是5.2倍.对于测试基准程序SHA,GSM,ADPCM,MPEG2,2种方式达到相同的性能提升.这是因为对于测试基准程序SHA,GSM,ADPCM,只枚举出了一个候选MCS(见表3).因此,精确算法和启发式算法的选择结果是相同的.对于测试基准程序MPEG2,由于候选MCS的数量太大,精确算法提供与文献[6]中的算法相同的结果.
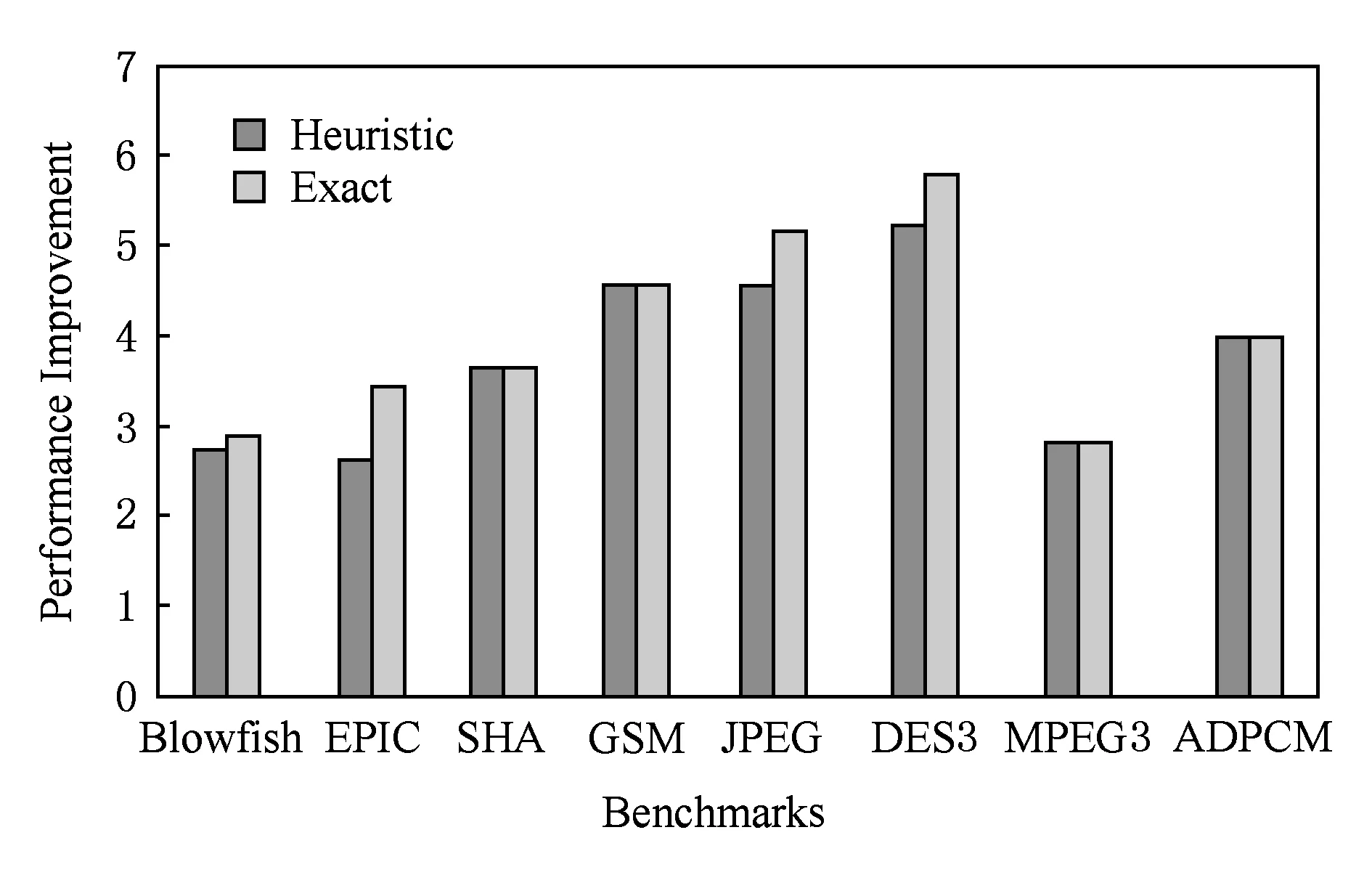
Fig. 8 Performance improvement of two algorithm[6]图8 2种算法[6]对性能提升的比较
7 总 结
本文提出了一种用于求解最大凸子图枚举问题的高效算法.该算法以夹心方式生成所有最大凸子图.夹心方式通过组合自下而上枚举方法和自顶向下方法,充分利用2种方法的优势.与最新算法相比,提出的方法可以实现数量级的加速,同时保证生成相同的所有最大凸子图集.此外,本文提出了使用精确选择算法的迭代识别流程,选择能够最大化提升性能的自定义指令集.与此前的启发式选择算法相比,所提出的精确选择算法可以实现对应用程序的更好的性能提升.
本文专注于选择最大凸自定义指令以最大化提升性能.由于低功耗已成为嵌入式领域研究的热点,因此在执行自定义指令识别时考虑功耗约束是很有必要的,这也是将来研究工作的重点之一.

