基于凸优化算法的参数不确定轮式移动机器人鲁棒PI控制

孙小康

（扬州高等职业技术学校，江苏 扬州　225000）

近些年机器人技术得到了飞速发展，呈现智能化、多元化趋势，并成功运用于国防、医院、工业和家庭等领域[1-2]。轮式机器人控制汇集了信息技术、机械技术以及传感器技术，是机器人研究领域中的一个重要分支，轮式机器人路径跟踪的精度影响着整个系统的性能[3-4]。然而轮式移动机器人又是一个多变量、强耦合、参数时变的非线性对象，难以对其进行高性能轨迹跟踪的控制[5]。近年来，随着现代控制技术的迅猛发展，一些现代控制方法被广泛地运用到了轮式机器人轨迹跟踪控制中，如反推（backstepping）控制[6]、变结构控制[7]、状态反馈线性化控制[8]、输入输出解耦控制[9]、组态方法[10]、粒子群优化算法[11]等。而文献[5]仅仅是针对轮式机器人的运动学模型设计路径跟随器，没有充分考虑系统摩擦力和参数不确定性对机器人运动性能的不良影响。

尽管传统的PID控制算法在移动机器人轨迹跟踪控制的研究上取得了一定成果，但随着环境的复杂化和不确定性，使得传统的控制方法已难以达到理想的控制效果。参数不确定对于系统产生的不良影响已经在全桥逆变器的控制领域中有所考虑，但在机器人控制系统中还有所欠缺[12]。

为此，本文主要研究参数不确定的轮式移动机器人路径跟踪控制问题。首先建立轮式机器人的动力学模型，并考虑摩擦力和环境的影响，进一步建立其参数不确定动力学模型。在此基础上设计一种基于凸优化算法的鲁棒 PI控制器，引入了 L1性能指标，并给出相关控制律，通过直接求解线性矩阵不等式即可得到控制器参数。最后，仿真结果表明该控制系统能够准确、快速地跟踪给定的参考路径，并能实现同时对给定的线速度、角速度和角度的跟踪。与常规的PI控制器相比，对于环境和摩擦系数变化产生的不确定性及扰动更具鲁棒性。

1　动力学模型

1.1　轮式移动机器人动力学模型建立

在绝对坐标系XOY固定平面内，移动机器人的运动示意图如图1所示。

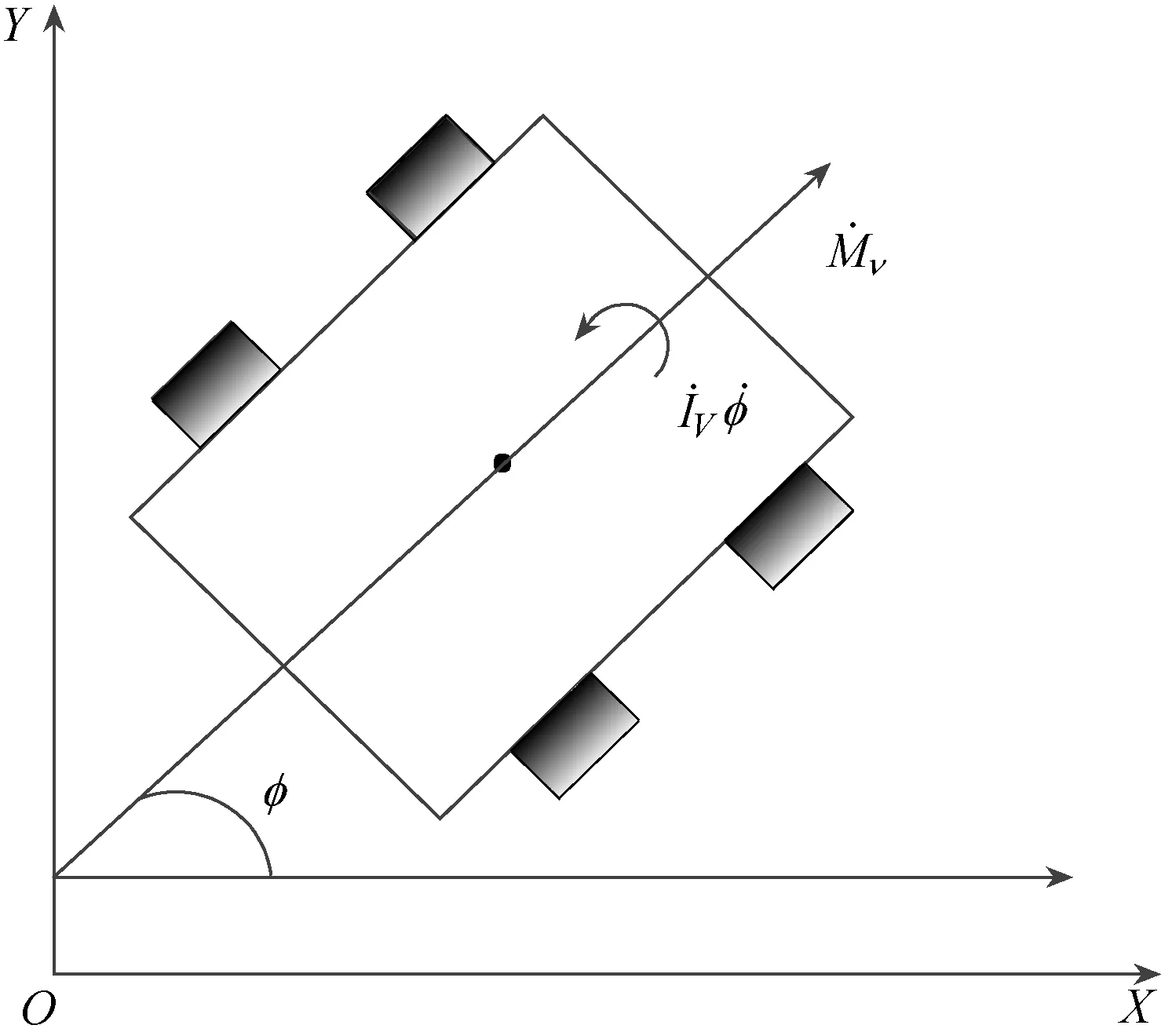
图1　移动机器人运动示意图

图1中，两个前轮为独立驱动轮，分别采用一组直流伺服电动机驱动，通过调节各自的输入电压控制两个前轮速度差，达到调整车体与跟踪路径的关系。而移动机器人的后轮为随动轮，仅起支撑车体的作用[5]。轮式移动机器人在忽略纵向滑动的条件下的动力学模型为[13-14]

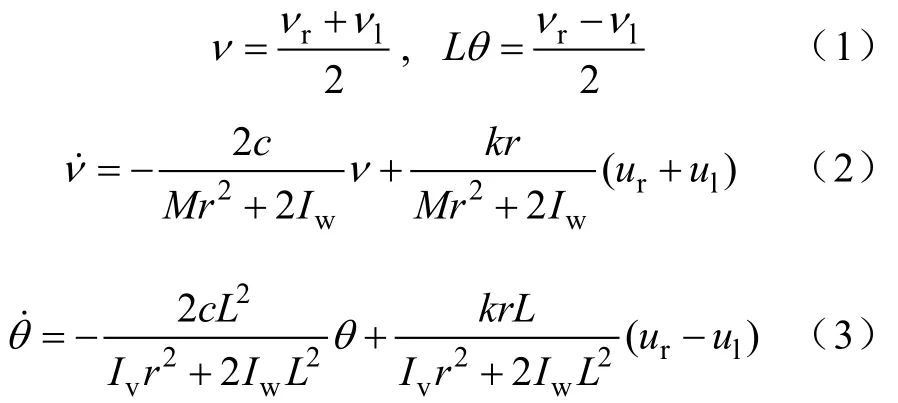
式中，ν为机器人前进线速度，ul和 ur分别为左右电机的驱动电压，νl和 νr分别为左右驱动轮的线速度，L表示机器人宽度的一半，φ 为机器人方向角，θφ=˙为机器人旋转角速度，c为轮胎与地面的摩擦系数，M为机器人总质量，r为车轮半径，k为驱动增益，Iv和Iw分别为绕机器人重心的转动惯量以及驱动轮的转动惯量。

定义：状态变量 x =[ν φ θ]T，控制输入 u =，输出变量 y= [ν φ]T，则根据式（1）至式（3）可得移动机器人的动力学状态方程为

其中：

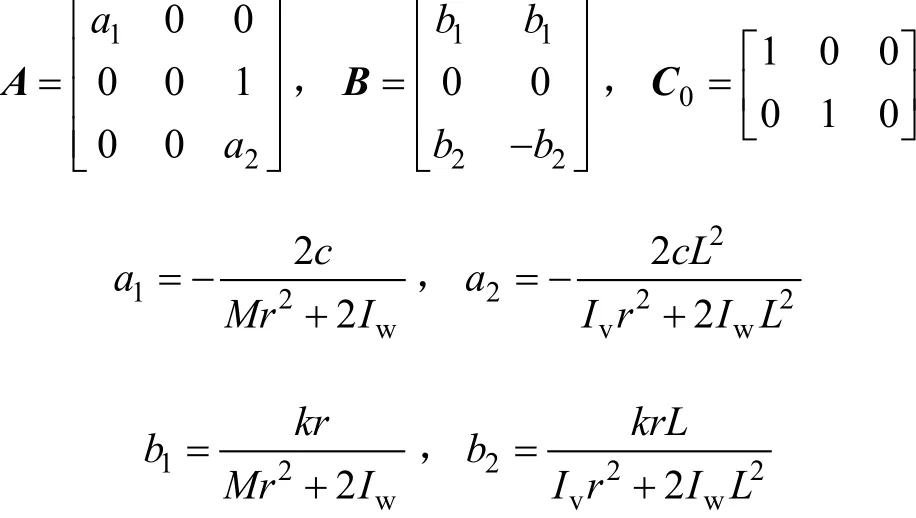
1.2　轮式移动机器人参数不确定模型建立

在实际应用中，移动机器人由于传动系统中减速器存在齿轮间隙，驱动电机的参数由于环境温度和路面摩擦系数的变化以及元件磨损等因素，都会引起伺服电机传动力矩的变化，因此，在控制系统的设计中，应充分考虑系统参数电机传动机构的驱动增益k、摩擦系数c的变化造成的影响。两种参数的不确定性描述为

此处，c0和 k0为相应的基准值，δc和δk分表代表了摩擦系数及驱动增益变化的比例，且满足δc≤Δc，δk≤Δk的条件，而Δc和Δk为已知的正常数。因此，轮式移动机器人的参数不确定模型构造如下：

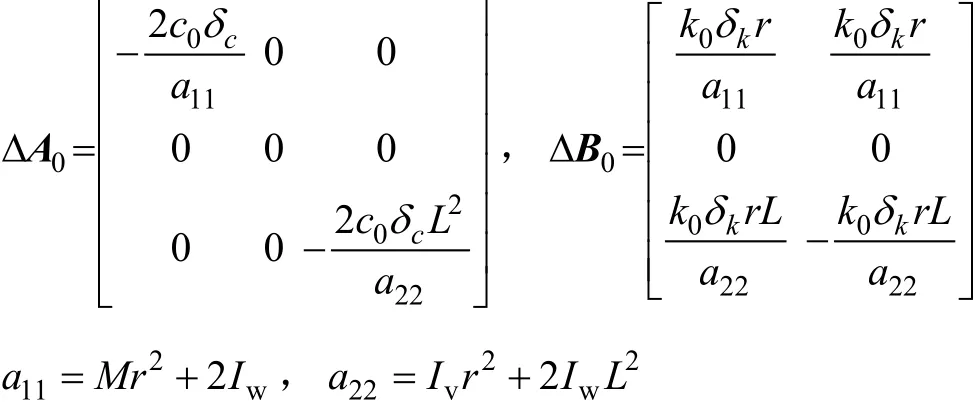
在系统（5）中，ΔA0和ΔB0为未知的不确定矩阵，同时满足如下条件：

F1(t)和F2(t)代表变扰动矩阵，并假设是Lebesque可测的。

2　控制器设计

为了高效便捷地解决系统的动态追踪问题，基于移动机器人的动力学参数不确定模型，设计如下的PI控制输入，即

式中，K=[KP1KP2KP3KI]为待求解的控制器增益，νd和φd为相应的目标值。

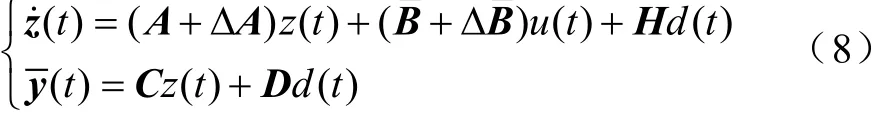
式中，y( t)为测量输出；矩阵C和D为适当维数常数矩阵，其他矩阵定义为

将u(t)=Kx(t)代入式（8），则相应的闭环机器人系统可以描述为

3　稳定性分析

定理1：对于给定参数 μi(i= 1 ,2)，εi(i= 1 ,2)和α＞0 ，若存在适当维数的矩阵， Q= P-1＞0、M=T-1＞0，R和常数γ＞0满足下列不等式条件：

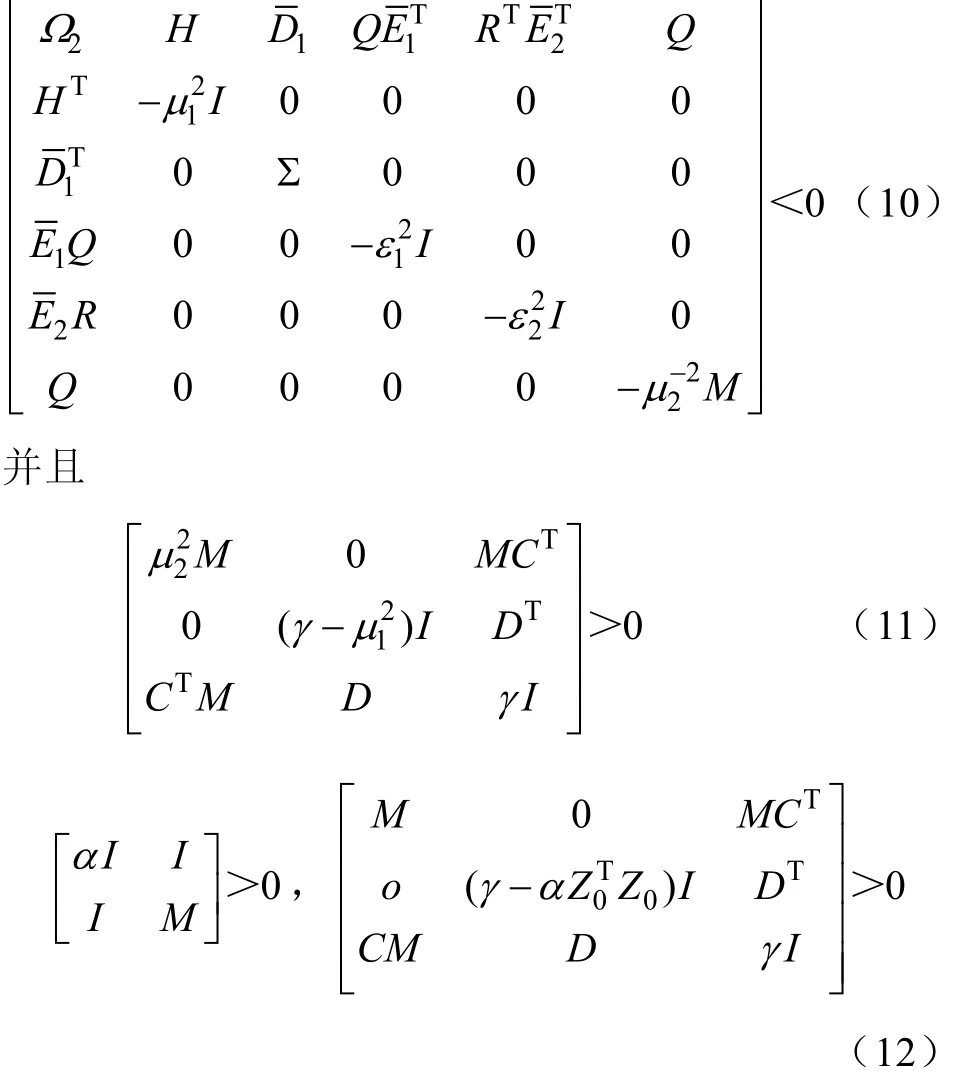
证明：选取Lyapunov函数 V ( z( t), t) = zT(t) P z( t )，易知 V ( z( t), t)≥0

进一步对其求导可得

在式（10）左、右乘以diag{P, I, I, I, I, I}，diag{P, I, I, I, I, I}，并结合Schur补引理，可以得到：(10)＜0⇔

成立；式中 z0(t)为初始状态向量，显然存在 d(t)的情况下闭环系统式（9）稳定。

下面讨论闭环系统的扰动衰减性能，式（19）可分为两种情形：

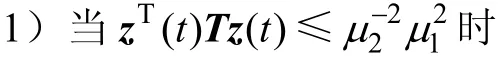
根据schur补引理，并在式（11）左右两侧分别左乘diag{,,}I IT和右乘diag{,,}I IT可得

进一步可以得到

同理，在式（12）左右两侧分别左乘diag{,}I T 和右乘diag{,}I T可得

进一步可以得到

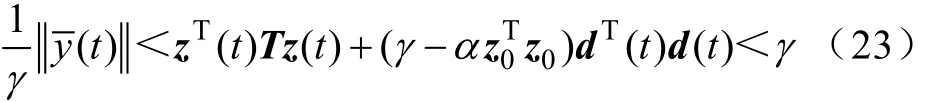
因此，闭环系统（9）满足扰动衰减L1性能指标。

最后，证明在控制输入 u(t)作用下系统的动态跟踪性能。假设θ1(t)和θ2(t)为闭环系统式（9）不同的两个动态轨迹。定义σ(t)=θ1(t)-θ2(t)，则关于信号的方程表述如下：

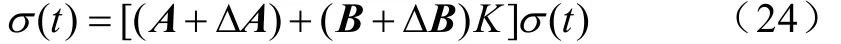
类似前述，选取Lyapunov函数如下：

基于不等式（10），同理可证：

式中，λmin(t)为 T的最小特征值。可得σ =0是系统惟一的渐近平衡点，同时意味着闭环系统式（9）存在惟一平衡点 z*，进一步可以得到跟踪误差积分收敛。因此，保证了闭环系统的跟踪性能。

4　仿真结果与分析

为了验证算法的有效性，分析参数c、k的变化对移动机器人运动控制系统的影响，本节在Matlab/Simulink平台上对所设计的鲁棒PI控制算法进行了仿真实验。实验中，分别选择正弦波形和圆形两种轨迹作为参考路径进行跟踪，更具一般性。机器人系统的物理参数见表 1。假定摩擦系数 c和驱动增益k的不确定量为δc=+10%，δk=+10%。同时选定矩阵不等式中相关参数如下：

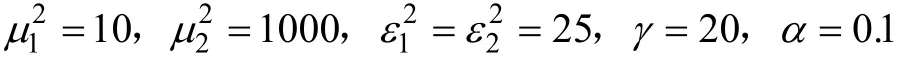
控制器增益通过直接求解线性矩阵不等式（10）至式（12）得到

表1　机器人物理参数

4.1　正弦波形轨迹跟踪

本节假设期望轨迹为 Y*=sin(0.2πX )的正弦波形，同时设定实际轨迹初始位置为(X ( 0),Y ( 0))=(0,0)，初始方向角 φ (0) = 0.2rad，初始角速度θ(0)=0.2rad/s，初始线速度ν(0) = 0.2m/s。期望线速度ν*=1m/s，期望角速度 θ*=φ˙=0.2πrad/s。

由图2至图4可知，设计的PI控制器使得轮式机器人系统在参数不确定条件下仍能快速地跟踪到速度和方向角的目标值，且跟踪误差收敛到零。由

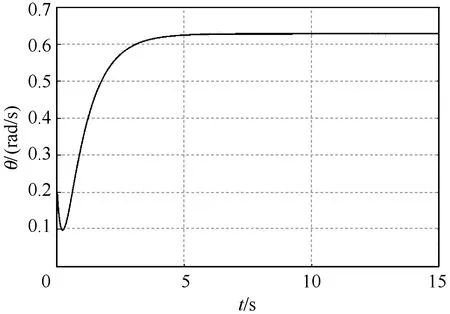
图2　线速度跟踪结果

图3　角速度跟踪结果

图4　跟踪误差

图5可知，机器人系统在控制器作用下快速、准确地跟踪到了设定的正弦波形轨迹，说明系统具备了良好的动态追踪性能和稳定性。

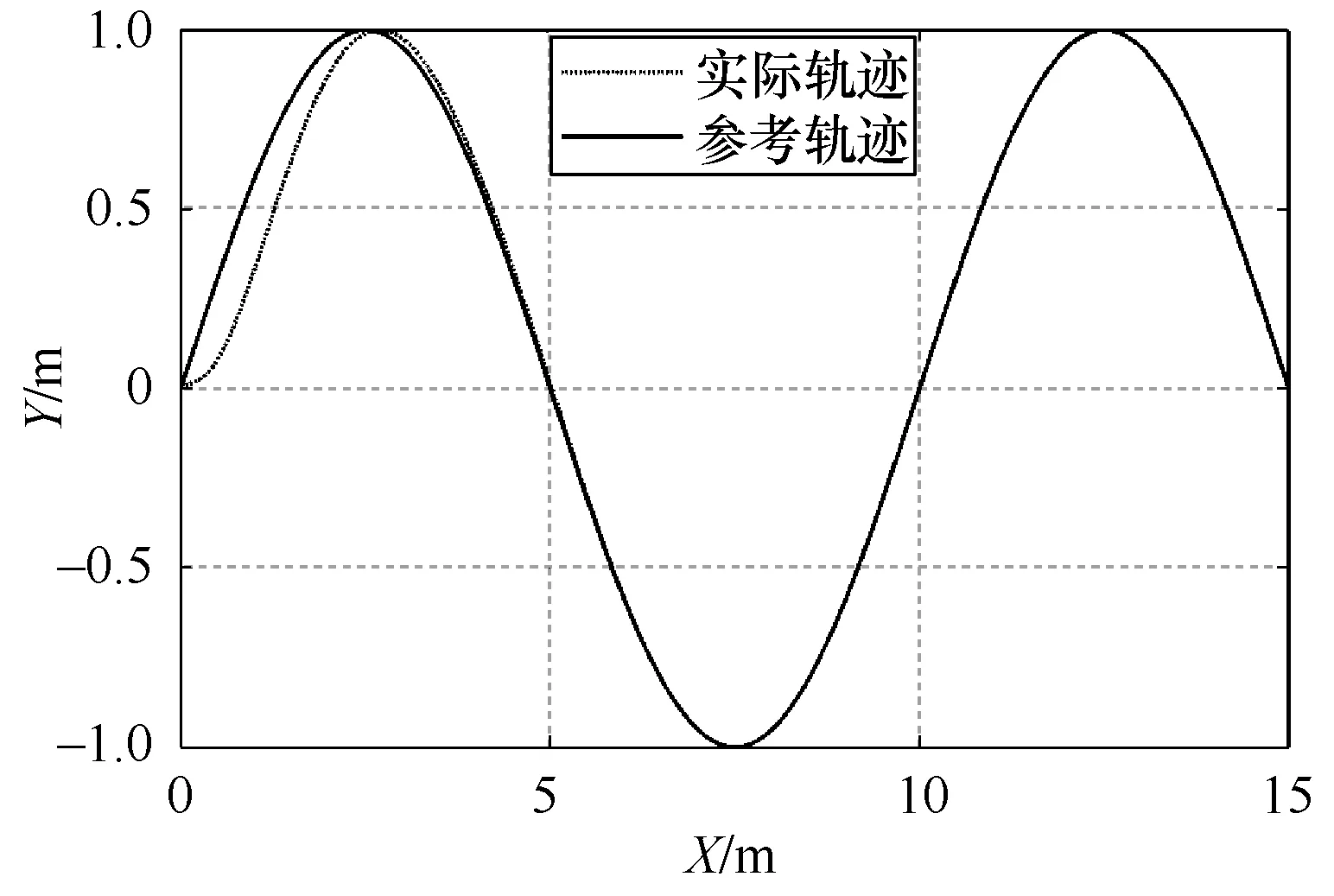
图5　正弦波形轨迹跟踪结果

4.2　圆形轨迹跟踪

本节假设期望轨迹为

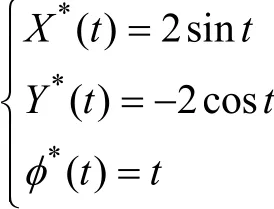
设定期望轨迹的初始位置为(X ( 0),Y ( 0))=(0.2,- 1 .4)，而实际轨迹的初始位置为(X ( 0),Y ( 0))=(1,- 1 )，初始方向角 φ ( 0 ) =0 .2rad，初始角速度θ( 0 ) =0 .35rad/s，初始线速度 ν ( 0 ) =0 .1m/s 。期望线速度ν*= 2 m/s，期望角速度 θ*=φ˙=1rad/s .

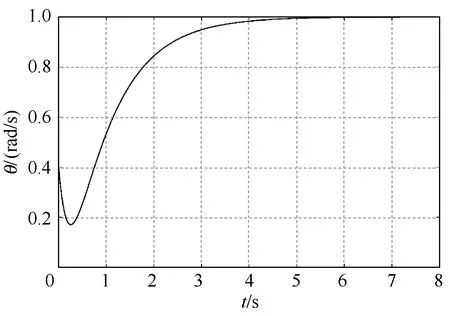
图6　线速度跟踪结果

图7　角速度跟踪结果

由图6和图7可知，设计的控制器能够使得参数不确定系统跟踪到设定的线速度和角速度。图 8说明了系统状态误差可以快速收敛到零。图9进一步验证了算法和控制器的有效性，尽管初始位置不一样，但控制器使得系统在跟踪圆形轨迹方面同样具备了良好的稳定性和动态跟踪性能。

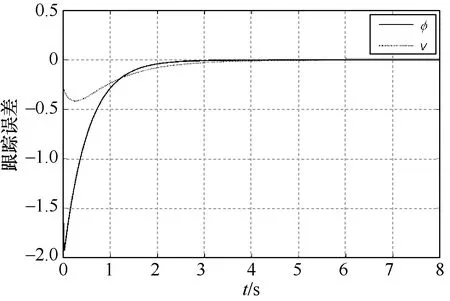
图8　跟踪误差

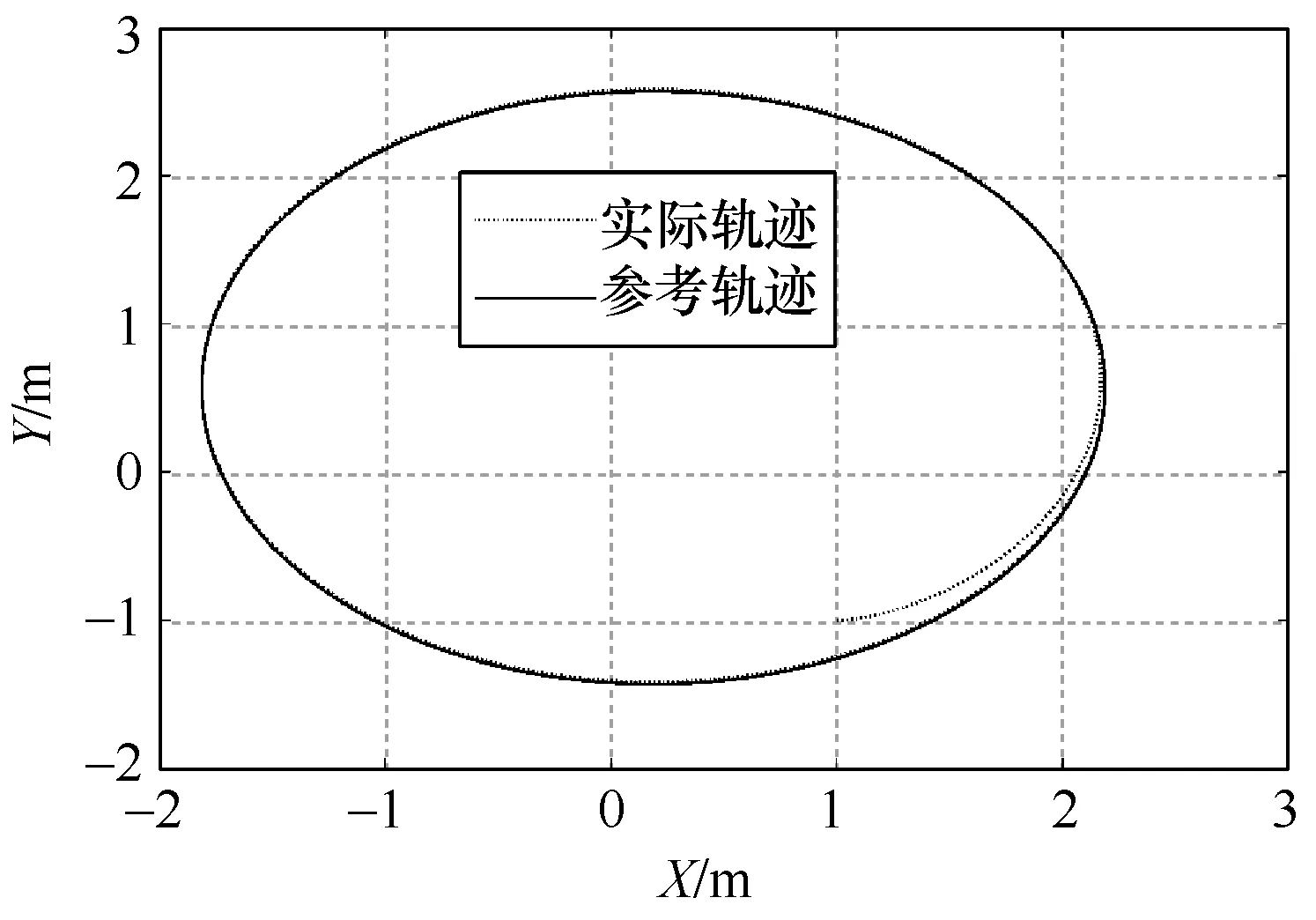
图9　圆形轨迹跟踪结果

5　结论

针对参数不确定的轮式移动机器人系统，本文设计了一种基于凸优化算法的鲁棒PI控制器，通过调节反馈控制输入使得移动机器人能够渐近地跟踪给定参考路径，并结合L1性能指标有效地抵制参数摄动的影响，增强系统的鲁棒性。同时，控制器也确保了轮式移动机器人的线速度、角速度和角度跟踪误差快速收敛到零。最后，基于Matlab平台的仿真结果进一步验证了设计算法的有效性。