关于伽利略斜面实验的思考

杨 君 丁庆红

(1. 北京教育考试院,北京 100083; 2. 北京教育学院石景山分院,北京 100043)

1 问题的提出

2014年北京高考理综卷第19题[1]是一道关于伽利略理想斜面实验的试题,原题如下.

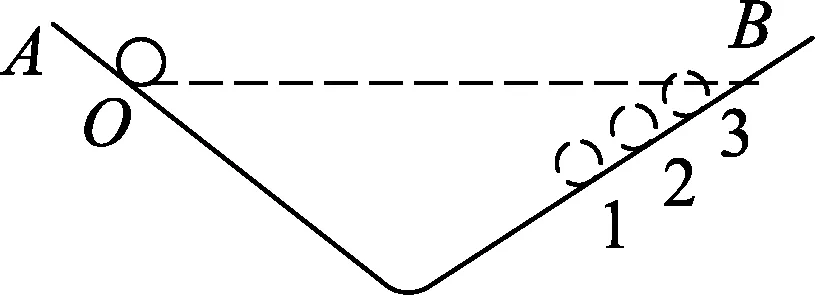
图1

伽利略创造的把实验、假设和逻辑推理相结合的科学方法,有力地促进了人类科学认识的发展．利用如图1所示的装置做如下实验:小球从左侧斜面上的O点由静止释放后沿斜面滚下,并沿右侧斜面上升．斜面上先后铺垫3种粗糙程度逐渐降低的材料时,小球沿右侧斜面上升到的最高位置依次为1、2、3．根据3次实验结果的对比,可以得到的最直接的结论是

(A) 如果斜面光滑,小球将上升到与O点等高的位置.

(B) 如果小球不受力,它将一直保持匀速运动或静止状态.

(C) 如果小球受到力的作用,它的运动状态将发生改变.

(D) 小球受到的力一定时,质量越大,它的加速度越小.

本题答案为(A),分析如下.

本题通过摩擦因素的实验提供考生逻辑推理的素材“斜面上先后铺垫3种粗糙程度逐渐降低的材料时,小球沿右侧斜面上升到的最高位置”越来越接近“与O点等高的位置”,这个现象中的变化因素是摩擦阻力越来越小,对应结果是“上升到的最高位置越来越接近与O点等高的位置”,所以这个实验得到的最直接的结论应该是选项(A)．选项(B)的内容是伽利略理想斜面实验两次理想过程之后才能得到的结论;选项(C)的内容与题干“3次实验结果对比”的要求不符合;选项(D)的内容是加速度与力和质量的关系的内容,题干叙述的定性实验无法得出这一定量表述．演示实验是物理教学的重要环节．课堂教学中,往往以演示实验为基础,或创设情景提出问题,或发现共性归纳结论,或通过实验验证规律,等等．学生在学习过程中,不仅要善于观察演示实验呈现的结果,还要有意识地应用把实验、假设和逻辑推理相结合的科学方法,以演示实验呈现的结果为基础,理清规律得出过程的层次性和逻辑性．

伽利略理想斜面实验是将实验、假设和逻辑推理相结合的典范,在教与学的过程中,既要重视实验的过程,也要重视逻辑推理的过程．深入理解伽利略理想斜面实验,深入挖掘其价值,对于物理教学和考试评价都有重要意义．

2 伽利略理想斜面实验

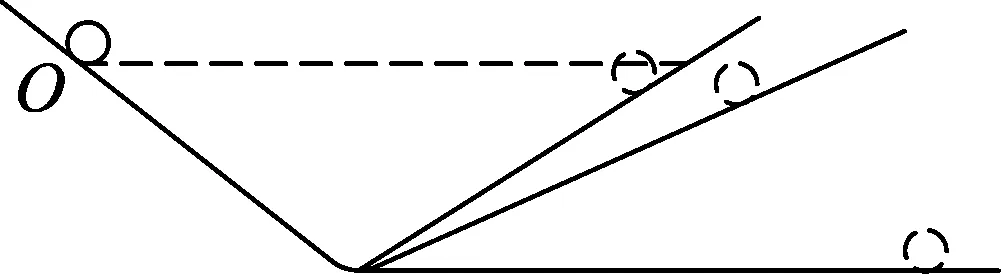
图2

伽利略为了说明力和运动的关系,设计了如图2所示的实验:让小球沿一个斜面从静止状态开始向下运动,小球将“冲”上另一个斜面,如果没有摩擦,小球将上升到原来的高度．减小第2个斜面的倾角,小球在这个斜面上仍将达到同一高度,但这时它要运动得远些．继续减小第2个斜面的倾角,球达到同一高度时就会离得更远．于是他问道:若将第2个斜面放平,球会到达多远的位置?显然:球将永远运动下去,却不再需要什么力去推动．这就是说,力不是维持物体运动的原因．

伽利略理想斜面实验应有两个层次．第一个层次是关于“摩擦”的理想化:“如果没有摩擦,小球将上升到原来的高度”;第二个层次是关于“运动”的逻辑推理:若将右侧斜面放平,小球将永远运动下去．前一各层次是第二个层次的基础,第二个层次是第一个层次的目标．显然,在实验过程中,最关键的因素是“摩擦”,这也是长期以来将人们引入歧途,认为“力是物体运动的原因”的根本所在．在实验过程中．由于不能消除完全消除空气阻力和摩擦力,也不能把第二个斜面做得无限长,所以伽利略的斜面实验是“理想实验”．

伽利略在“关于两门新科学的对话”[2]中对斜面实验的描述是:“取大约12库比特长、半库比特宽、三指厚的一个木制模件或一块木料,在上面开一条比一指稍宽的槽,把它做得非常直、平坦和光滑,并且用羊皮纸给它划上线,羊皮纸也尽可能地平坦和光滑,我们沿着它滚动一个硬的、光滑的和非常圆的黄铜球．”可以看出,为了减小摩擦的影响,伽利略选用了“硬的、光滑的和非常圆的黄铜球”,而且“羊皮纸也尽可能地平坦和光滑”．那么,实际实验过程中,是否摩擦系数越小,实验效果越好呢?伽利略是贴上了羊皮纸,使斜面光滑．但郭奕玲、沈慧君编著的《物理学史》[3]第17页中说:“有人证明,贴了羊皮纸的木槽,实验误差反而更大了．”什么原因?实心的黄铜球是否可以用其他诸如空心金属球、圆柱、圆环等替代呢?实验效果如何?下面将从定性和定量两个角度对上述问题予以分析．

3 关于实验的思考

小球沿斜面下滑的过程中,受到摩擦力和空气阻力.空气阻力与速度有关,速度越大空气阻力越大;一般而言小球下滑过程即不是纯滑动,也不是无滑滚动,而是连滚带滑,所以摩擦包括滑动摩擦和滚动摩擦．空气阻力可以通过降低斜面高度来减小.在忽略空气阻力的前提下,若斜面理想光滑,则小球沿斜面下滑(无滚动),则小球运动过程中无能量损失;若小球沿斜面无滑滚动,则由于一对静摩擦力不做功,小球运动过程中动能(包括转动动能)和重力势能相互转化,机械能守恒;在连滚带滑的情况下,则小球滑动过程中因摩擦生热将会损失机械能.

实际实验过程中,理想的光滑斜面是不可能的,但可以通过减小滑动摩擦因数逼近理想的纯滑动.这种情况比较简单.下面重点讨论无滑滚动.若斜面过于光滑,则小球易于滑动而难以滚动,此时机械能损失主要为滑动摩擦产生的热能;若斜面过于粗糙,虽小球易于滚动,但小球相对斜面仍有滑动,较大的摩擦因数也会带来较大的能量损失．为了逼近理想情况,应该在实现无滑滚动的同时减小摩擦因数,避免由此带来的机械能损失.

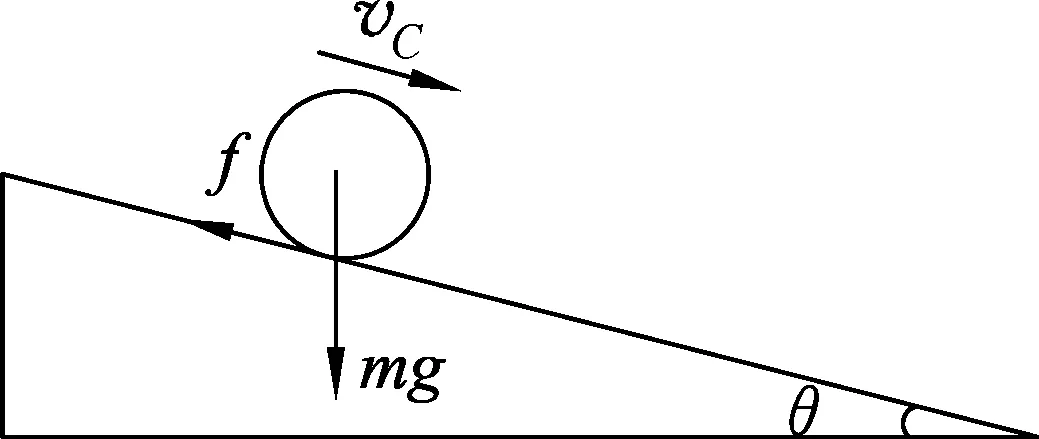
图3

为说明问题,下面定量分析小球沿斜面无滑滚动的条件．如图3所示,小球质量为m,与斜面的静摩擦因数为μ,斜面倾角为θ．

小球在下滚过程中,由牛顿第二定律

mgsinθ-f=maC，

(1)

其中aC为质心的加速度．

对于质心,重力的力矩等于0,只有摩擦力f的力矩,τf=Rf.

(2)

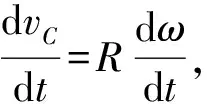
aC=Rα.

(3)

联立(2)、(3)式得

(4)

联立(1)、(4)式得

代入(4)式得

要使小球保持无滑滚动,所需静摩擦力不能大于最大静摩擦力,设最大静摩擦力

fmax=μN=μmgcosθ.

则f≤fmax,得

(5)

对于无滑的上滚过程,vC减小,ω亦减小,平动和转动都是减速的,受力及运动情形如图4所示．

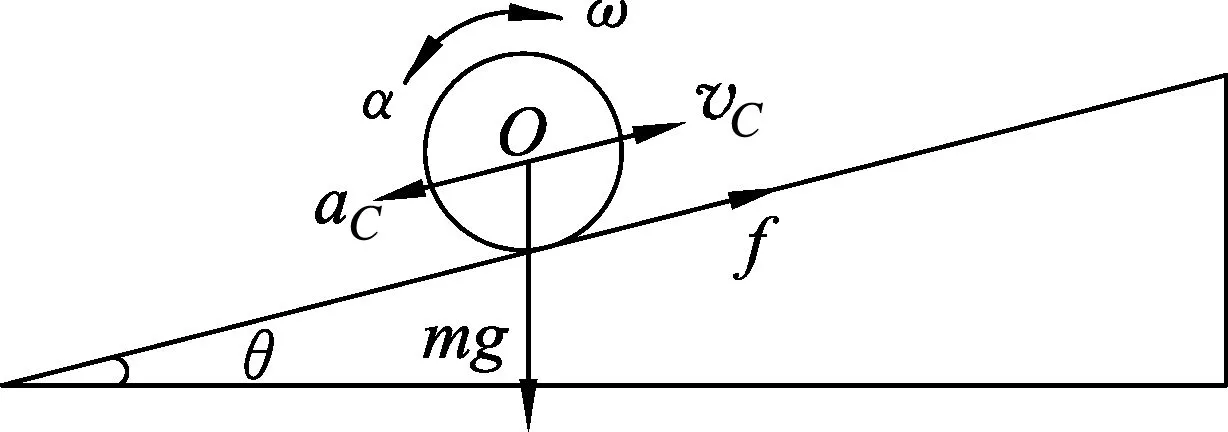
图4

由方程(1)和(4)可以看出,上滚和下滚的情形是相同的．

同理,对于圆环、空心圆桶、实心圆柱或空心小球,也可计算出实现其无滑滚动的条件．结果如下:

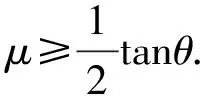
通过上述分析,可以得出两个结论：(1) 小球沿斜面做无滑滚动,斜面的静摩擦因数有一极小值,且极小值与斜面倾角有关．(2) 若采用同一倾角的斜面,相比其他物体,实心小球实现无滑滚动对应的静摩擦因数的极小值最小,即实心小球相对容易实现无滑滚动．因此,为提高实验精度,应一方面选择实心球体进行实验,另一方面,应尽可能使斜面的静摩擦因数接近于实现无滑滚动的极小值．

4 伽利略斜面实验的伟大成就

伽利略理想斜面实验是最美的实验之一．克里斯著《史上最美的十项科学实验》,[4]George Johnson著《历史上最美的10个实验》[5]两本书中均收录了这个实验．其中克里斯评论说:“伽利略的斜面实验本身就具有独特的美．事实上,伽利略的斜面实验,是种‘模式浮现’之美．这项实验的美是在于它的戏剧性作法,只用了相当单纯的装置,就能够让自然的基本原理生动展现,而乍看之下,这只是一组随机、混乱的事件——圆球滚落坡道．这就是那项定律最初向伽利略展现的方式,而今它也是以这种方式对学生展示．”

虽然从伽利略斜面实验还不足以判定伽利略发现落体定律的全过程,但可以窥视到伽利略研究运动学的方法．他把实验和数学结合在一起,既注重逻辑推理,又依靠实验检验,这就构成了一套完整的科学研究方法．可见,伽利略理想斜面实验蕴涵着方法美．正是伽利略把实验和逻辑推理和谐地结合在一起,有力地推动了科学的发展．伽利略的墓志铭上书:“他失明了,因为自然界已经没有剩下什么他没看见过的东西了．”是啊,的确如此!对于伽利略的成就和获得成就的方法,爱因斯坦的赞扬最具有代表性:“伽利略的发现以及他所应用的科学的推理方法,是人类思想史上最伟大的成就之一,而且标志着物理学的真正开端．”

5 对中学物理教学的启示

5.1 做好伽利略斜面实验,向学生展示实验之美

伽利略斜面实验装置几百年前就做得出来,我们现在更有理由和学生一起做好这个实验,让学生体会伽利略斜面实验具有原始的朴素美,它用最简单的装置——一个小球和一个斜面,展示了自然界最深刻的道理．

5.2 分析伽利略斜面实验,向学生展示方法之美

伽利略关于运动的研究中,斜面是他采用的最基本的思考问题的方法．在自由落体运动规律的研究中,他首先想到用斜面来”减小”引力作用,保证时间成为可测量的物理量．他从斜面外推到落体运动,通过逻辑推理得到落体运动的时间平方关系;进而通过斜面实验验证斜面的匀加速运动符合时间平方关系,间接证明落体运动也符合时间平方反比关系,与他的逻辑推理一致．在对惯性定律的研究中,他通过理想斜面实验得出结论:力是改变物体运动状态的原因．理想斜面实验,它来源于对真实实验或生活经验的逻辑推理或者是思辨,最终表述为牛顿第一定律．所以,无论是理想斜面还是真实斜面,都很明确地反映了伽利略研究问题的科学方法——实验+逻辑推理．虽然牛顿第一定律和落体运动定律是两个独立的物理规律,但是斜面实验将其二者联系在了一起,也体现出伽利略斜面方法在其研究中的连续性．因此,在理想斜面实验的教学中重点培养学生的是一种逻辑推理能力．

伽利略还指出,在科学研究中,懂得忽略什么,有时与懂得重视什么同等重要．

5.3 充分运用伽利略斜面实验追寻守恒量

深入研究伽利略斜面实验可以发现,能量及其守恒的思想,在伽利略的实验中已经显现出来了．如图1所示,在这个实验中,小球一旦沿斜面A滚落,它就要继续滚上另一个斜面B．重要的是,伽利略发现了具有启发性的事实:无论斜面B比斜面A陡些或缓些,小球的速度最后总会在斜面上的某点变为0,这点距斜面底端的竖直高度与它出发时的高度相同．看起来,小球好像具有灵性,“记得”自己起始的高度,或与高度相关的某个量．这说明某种“东西”在小球运动过程中是不变的,这个“东西”就是能量．