杆会滑离墙面?——基于问题链式的习题探究

吴文肖

(遵义市第三中学,贵州 遵义 563000)

问题链是中学物理教学中重要的教学方法,无论是教师教法指导还是学生学法养成抑或是题目命制与拓展,都可以取得较好的实践效果．

本文笔者基于问题链方法讨论刚性轻杆系统弹力突变问题.

1 文本信息反馈

图1

题目.如图1所示,小球a,b的质量均为m,a球套在竖直的光滑导轨上,与水平面相距h.b放在地面上,其中a,b通过铰链用刚性轻杆连接,轻杆的长度为l．现从静止开始释放,a,b可视为质点,重力加速度大小为g.则

(A)a球落地前,系统机械能守恒.

(B)a下落过程中,其加速度大小始终不大于g.

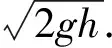
(D)a落地前,当其机械能最小时,b对地面的压力大小为mg.

解析： 对于a,b杆的连接体系统,下滑过程中只有动能及重力势能相互转化,故系统机械能保持不变,故选项(A)正确．下滑过程中,杆对a球的弹力先表现为推力后是拉力,当杆对a表现为拉力时,加速度可以大于g,故选项(B)错误．落地时,a球的速度方向竖直向下,沿杆长方向的分速度为0.由刚性杆不可伸长知，沿着杆的分速度始终相等,易判断b球也为0,故选项(C)错误．杆对a球先是推力后是拉力,既有负功过程又有正功过程,机械能最小时正是杆的推力变拉力的瞬间,此时刚性轻杆的作用力为0,对b球竖直方向运用二力平衡可得，b对地面的压力大小为mg,故选项(D)正确．

点评： 本题借助连接体模型,重点考查了机械能守恒,功能关系及矢量合成与分解等物理知识，训练了学生物理建模思想,运用数学解决物理的分析能力和推理能力．在中学生基础物理中层次性较高,区分度较好,是一道颇具遴选功能的好题．

2 思考与假设

假如将上题中的题设条件“a球套在光滑轻杆上”改为“斜靠在光滑的墙面上”,球a会滑离开墙面吗?如果会,滑离时距离地面高度多少?杆与墙面的夹角为多少?

3 提出问题与应对措施

问题1： 下滑的刚性杆系统弹力何时突变为拉力?(捕捉时间点)

措施1： 深度审题,巧抓“关键态”.

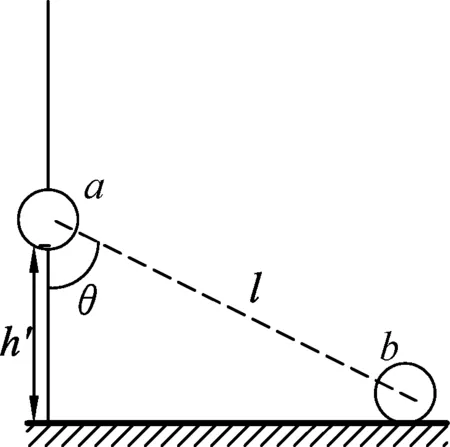
图2 弹力临界图

为了便于计算、推导,仍以原题为探究背景展开分析．设a球下滑至距地高度为h′时,速度为va,而b球速度达到最大值vb,刚性杆与墙面夹角为θ，如图2所示.

在上述问题中,对刚性杆系统,在下滑过程中什么时候推力会突变成拉力?这个力的关键转折点在哪儿呢?从b球的运动规律知道,杆对b球先是推力后是拉力,即先对b做正功再做负功,其动能先增大后减小．b球最大动能时就是杆弹力突变临界点.

问题2： 在何位置a球滑离墙面?(定位空间位置)

措施2： 活用不等式,妙解临界值.

由a,b杆系统机械能守恒易得

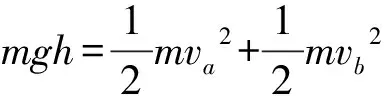
而a,b球沿着杆的速度满足关系

vacosθ=vbsinθ．

将上式化简为va=vbtanθ,并代入上式,整理得

vb2=2g(h-h′)cos2θ.

(1)

根据几何知识易知

代入(1)式可得

(2)

对于式(2),可采用均值不等式化简(或导数法,此处暂不赘述,读者可自行推导).

(3)

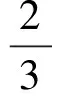
问题3： 滑离时刚性杆与竖直墙面夹角多大?(描绘物理结构)

措施3： 理论升华,返璞归真.

(4)

为了更直观描述刚性杆的其他脱离情况,笔者采用控制变量法,分别统计了等高度不同长度和等长度不同高度刚性轻杆系统沿光滑墙面下滑时的杆与墙面的夹角(以下称“脱离角”)情况,如表1,以供读者查阅借鉴之用．

表1 不同长度(或不同高度)刚性杆下滑参数

表中信息表明： (1) 对于刚性轻杆,滑离墙面时的高度与杆长l无关,只取决于靠墙高度h; (2) 靠墙高度相等(不相等)时,脱离高度一样(不相等),杆越长(或杆等长),脱离角越大(小).

在理论物理中,刚性杆组成的力学体系所含的物理信息很丰富,只有详细解剖其动力学规律,才可以取得举一反三的效果．在具体的研究对象下,问题链式的设计流程通过采取文本反馈物理讯息、大胆思考并提取核心问题点、采取有效的物理措施等环节使得知识与逻辑反复滚动倾轧,促进了心理认知的发展．基于问题链式的科学探究,学生思维跨度小,知识网格化紧密,理性逻辑承前启后,有助于学生在具体的教育环境中,积极主动地获取知识,发展能力．因此,学习物理,应时刻胸怀严谨务实之求真精神,科学之探究方法,方能做到拨云见日,尽览物理之余美．