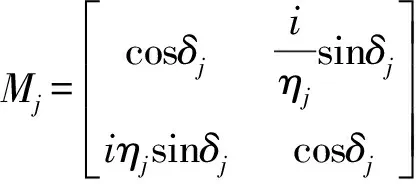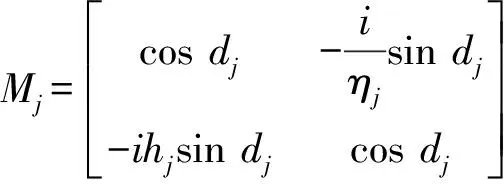关于金属材料复折射率符号的讨论及运用

殷嘉琳 王 妍 钱 敏, 2*

(1.苏州大学文正学院电子工程系,江苏 苏州 215104;2.苏州大学电子信息学院微电子系,江苏 苏州 215006)

在科学研究过程中,比如电磁场理论(电动力学)、光学、薄膜光学、半导体光电等,会涉及到材料的折射率,包括有耗介质金属材料的折射率.在不同的资料中,有关金属材料折射率提供了两种形式.在电动力学中[1],形式为N=n+ik,其中n称为常规折射率,k称为消光系数.在薄膜光学[2-3]、半导体光电[4]中提供的形式为N=n-ik.这给大家在计算过程中造成困扰.与折射率密切相关的一个参数是介电常数,根据经典电磁理论,折射率是介电常数的平方根.金属材料的介电常数与电磁波频率有关,所以改称介电函数.有文献资料[5-7]曾对该问题进行简单的讨论:提出造成金属介电函数有不同形式的原因是在推导过程中电磁场的波动形式采用了两种形式:e-i ω t和ei ω t.固然是如此,那到底在使用介电函数进行计算时,采用哪个形式呢?这给大家造成了一些困扰,笔者就该问题进行了比较深入的研究.

1 金属电子气极化及Lorentz-Drude模型

物质材料的介电常数取决于物质在外电场作用下的极化特性.一般由电子位移极化、离子位移极化、固有偶极矩取向极化组成.金属内部存在大量的近自由电子,可将金属晶体理解为淹没在电子海洋中的正离子实点阵,一般不具有固有偶极矩.同时由于原子核(离子实)与电子质量相差悬殊,对电特性研究,离子运动可以忽略,故离子位移极化亦可忽略不计,因此,金属的极化特性决定于自由电子位移极化.

根据经典电磁理论,无外电场时,电子进行绕核运动,正负电荷的中心重叠,因此固有偶极矩为0;当加外场后,电子轨道偏移造成正负电荷中心分离,产生偶极矩,通常称为感生电偶极矩.如何计算感生电偶极矩,必须采用一定的模型.经典方法是将绕核运转的电子视为束缚谐振电子,弹性恢复力属于束缚力,还受到辐射阻尼力,可以得介质中外场作用下电子的运动方程,电磁场形式采用e-i ω t形式:

其中ω0是电子固有束缚振动频率,ω是外场频率,γ是阻尼系数.上式的解的形式为

x=x0e-i ω t.

求出各阶导数,代入运动方程后并根据相对介电常数的定义得到

其中

以上假定金属中单位体积中有N个原子,每个原子有Z个电子,NZ是单位体积内的电子数,电子固有束缚振动频率均为ω0,ωp称为体等离子体频率.所有电子的固有束缚振动频率都为ω0,阻尼系数都为γ.但实际上,原子中电子可能存在多个束缚振动频率和阻尼系数.假设每个原子中的电子有K种振动频率和阻尼系数,束缚振动频率为ωj、阻尼系数为γj的电子有zj(j=0,1,2…K)个,则可将上式改写为

(1)

其中f0为自由电子比例,fj为固有频率为ωj的束缚电子比例,其中γ0也是辐射阻尼系数.约束条件为

这就是最终形式的金属相对介电常数.由于是外场频率ω的函数(是一个复数),所以又称为介电函数,该模型称为Lorentz-Drude模型.[8]需要说明的一点是,以上推导过程仅仅是一种模型而已,并不能完全说明介电函数的全部成因;实际的结果通常以实验测试值为准,相关参数通常根据该模型通过拟合得到,并不一定满足约束条件,此时改称fj为强度因子.[9]表1、2列出了Ag和A1金属材料相关拟合参数.

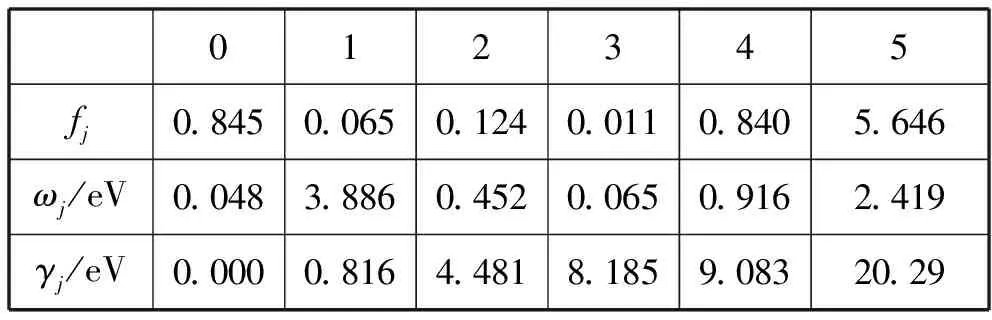
表1 Ag的复介电函数相关参数(ωp=9.01/eV,LD模型)

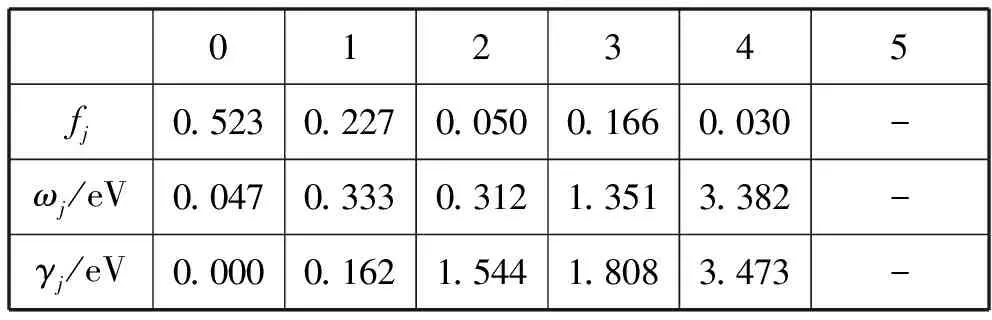
表2 Al的复介电函数相关参数(ωp=14.98/eV,LD模型)

2 高频近似Drude模型

当外场的频率远远大于原子中电子的束缚频率时(比如可见光频段),金属中的电子可视为是自由的,且阻尼可忽略不计,此时金属对电磁波的作用类似于由离子和自由电子组成的电离气体(等离子体)对电磁波的作用,此时金属的相对介电常数可由公式(1)作高频近似后得到

(2)

这就是自由电子的Drude模型;[10]在不忽略阻尼的情况下,近自由电子的介电常数可表示为

(3)

根据电磁场理论,我们知道,非磁性介质材料的折射率是介电常数的平方根;根据公式(3)可知,金属材料的折射率N也是一个复数.简单推导可以得到,折射率有N=n+ik的形式,实部n是通常的折射率,k是消光系数(k>0),它表示了电磁相互作用时,材料对电磁波的衰减作用.值得指出的是,以上推导过程,电磁波的形式采用了负指数形式;假如电磁波形式采用正指数ei ω t形式,那么最终推导的结果形式为

(4)

此时折射率有N=n-ik的形式,k>0.必须注意的是,在光学计算的过程中(比如薄膜光学特征矩阵的形式会不同),必须采用相应的形式,才能得到正确的计算结果.总结如下:

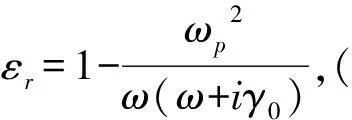
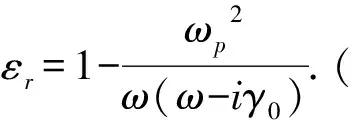
3 金属复介电函数和复折射率

根据复介电函数和复折射率的平方关系,画出幅角关系如图1所示.

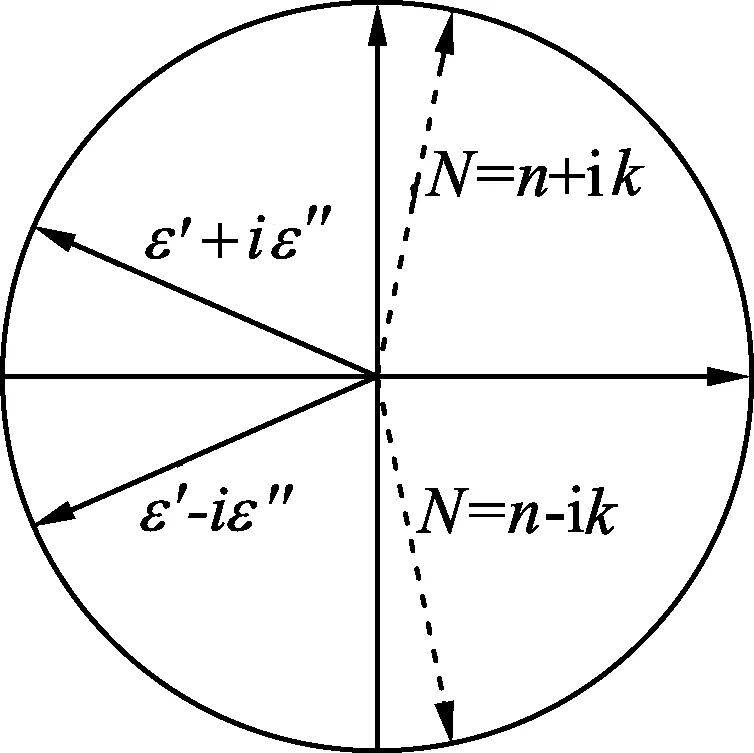
图1 金属复介电函数与复折射率之间辐角的关系

根据公式(2)(3),一般当光频小于等离子体频率时,金属的复介电函数的实部ε′<0,ε″取绝对值(>0),所以可见光频段金属被称为负介电常数材料.根据复数运算规则可见,两种形式下,介电函数、折射率的实部和虚部的绝对值是一致的.通常金属介电函数的实部绝对值比虚部绝对值大较多,导致复折射率的实部绝对值比虚部绝对值小较多.

事实上,这两种形式的复折射率对于电磁波在金属等有耗介质中的衰减传播形式是一致的,如下两式所示.

eiωt形式，N=n-ik:

e-iωt形式，N=n+ik:

由此可见,负指数衰减部分的形式是一致的.表3列出了常见金属材料的复介电常数和复折射率.

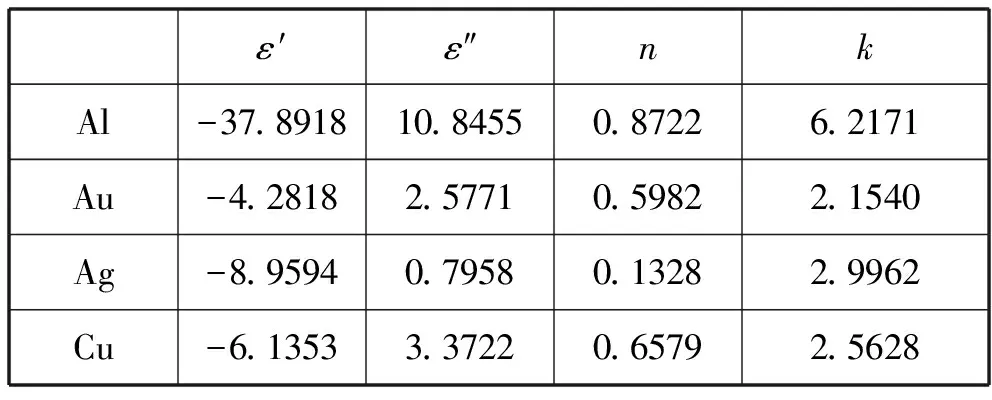
表3 常见金属材料的复介电常数和复折射率(@λ=528 nm,LD模型)[9]

4 折射率形式在薄膜光学计算中的运用

采用不同的电磁波振动因子形式,推导薄膜光学计算中相关计算公式,必须与相对应的金属介电函数配套使用;否则计算就会出现差错.

如含金属薄膜层的振幅分割的多光束薄膜干涉计算:

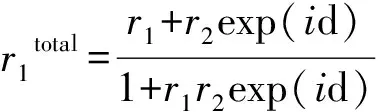
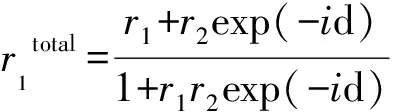
如用传输矩阵法计算含金属薄膜层的多层介质的透射系数和反射系数: