第34届全国中学生物理竞赛预赛中的数学技巧

林庆新 李志雄

(1. 莆田市教师进修学院，福建 莆田 351100; 2. 莆田第十中学，福建 莆田 351146)

第34届全国中学生物理竞赛预赛命题的突出特点是注重数理结合,对数学应用能力要求高,下面将揭示试题多次涉及的数列和递推等高中数学的方法和技巧．

例1.(第34届预赛第8题)某一导体通过反复接触某块金属板来充电．该金属板初始电荷量为6 μC,每次金属板与导体脱离接触后,金属板又被充满6 μC．已知导体第一次与金属板接触后,导体上带的电荷量为2 μC;经过无穷次接触,导体上所带的电荷量最终为________．

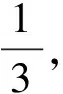
将两式相减得

利用上式,令n从1开始递增至n,将得到的递推关系式分行展开(并注意题给条件).

q1=2，

……

将以上各式等号左边各项累加(将逐项相消至剩一项),等号右边各项累加,得到

利用等比数列求和公式得

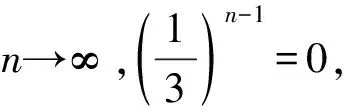
或且注意到经过无穷次接触后,导体上所带电荷量不再变化,即当n→∞时,有

解得qn=3 μC.

例2.(第34届预赛第15题),如图1,某根水平固定的长滑竿上有n(n≥3)个质量相同的滑扣(即可以滑动的圆环),每相邻的两个滑扣(极薄)之间有不可伸长的柔软轻质细线相连,细线长度均为L,滑扣在滑竿上滑行的阻力大小恒为滑扣对滑竿正压力大小的μ倍．开始时所有滑扣可近似地看成挨在一起(但未相互挤压)，今给第1个滑扣一个初速度使其在滑竿上开始向左滑行(平动)，在滑扣滑行的过程中,前、后滑扣之间的细线拉紧后都以共同的速度向前滑行,但最后一个(即第n个)滑扣固定在滑竿边缘．已知从第1个滑扣开始的(n-1)个滑扣相互之间都依次拉紧,继续滑行距离l(0

(1) 滑扣1的初速度的大小;

(2) 整个过程中克服摩擦力所做的功;

(3) 整个过程中仅仅由于细线拉紧引起的总动能损失．

图1

解析: 此题是计算题,下面的解答将给出比参考解答更严谨和清晰的分析．

(1) 先探讨一个运动物体和一个静止物体碰撞后,发生完全非弹性碰撞前后的能量变化．设两个物体质量分别为m1和m2,初速度分别为v1和0,发生完全非弹性碰撞后共同速度为v,则碰前的动能为

(1)

由于细绳拉紧前后时间间隔极短,可以忽略摩擦阻力,故前后动量守恒,有

m1v1=(m1+m2)v.

(2)

碰后的动能之和(即系统剩余动能)为

(3)

由(1)～(3)式得

(4)

设第一个滑扣以速度v10开始运动,其动能为

(5)

在第1个滑扣滑动距离L、第1与第2个滑扣之间的细绳刚拉紧前的瞬间,系统剩余动能为

E1f=E10-μmgL.

(6)

此后第1个滑扣与第2个滑扣拉紧(发生完全非弹性碰撞),2个滑扣共同滑行距离L后与第3个滑扣拉紧,3个滑扣共同滑行距离L后又与第4个滑扣拉紧……

设第k-1个滑扣与第k个滑扣拉紧后的动能为Ek0(即k个滑扣开始滑行的动能),共同滑行距离L后的动能为Ekf,则有

Ek0-kμmgL=Ekf.

(7)

第k个滑扣与第k+1个滑扣拉紧后的动能为E(k+1)0,则由(4)式结论有

(8)

由(7)、(8)式可得

(k+1)E(k+1)0-kEk0=-k2μmgL.

(9)

令k从1开始递增至k-1依次代入(9)式,将得到的递推式分行排列如下.

2E20-E10=-12μmgL，

3E20-2E10=-22μmgL，

4E20-3E10=-32μmgL，

……

kEk0-(k-1)E(k-1)0=-(k-1)2μmgL.

将以上各式等号左边各项累加(注意相消),等号右边各项累加,可得到

kEk0-E10=

-[12+22+32+…+(k-1)2]μmgL.

(10)

(11)

利用上式结论,从第1个滑扣开始的(n-1)个滑扣相互之间依次拉紧后的动能为

(12)

依题意,这(n-1)个滑扣共同滑行l(0

E(n-1)0=(n-1)μmgl.

(13)

由(5)、(12)、(13)式得

(14)

(2)整个过程中克服摩擦力所做的功为

W=μmgL[1+2+3+…+(n-2)]+μ(n-1)mgl.

利用等差数列公式得

(15)

(3)整个过程中仅仅由于细线拉紧引起的总动能损失为

ΔE=E10-W.

(16)

由(5)、(14)～(16)式得

23-13=3·12+3·1+1，

33-23=3·22+3·2+1，

……

(n+1)3-n3=3n2+3n+1.

将以上各式等号左边各项累加,等号右边各项累加,可得到

整理得