系列伺服作动器动态加载系统及其控制策略*

游有鹏， 荣　亮

(南京航空航天大学 机电学院， 南京 210016)

在导弹制导与控制过程中，伺服作动器作为导弹控制系统中的重要执行机构，其性能优劣直接影响到导弹的操控性和稳定性，因而利用地面的试验设备对伺服作动器系统的各项性能指标进行测试是其设计过程中的重要环节[1-2].

随着电机技术和电液伺服技术的快速发展，目前常见的加载方式主要包括电动加载和电液加载.文献[3]利用加载液压缸对船舶舵机进行力加载，采用机理建模法并基于MATLAB/Simulink建立了加载系统数学模型并进行了仿真试验，但由于液压系统是一种非线性时滞系统，且常规建模方法对系统进行了相应简化，因此，无法准确地描述系统特性，且该系统的加载频率较低，因而不适用于高频加载的情形.文献[4]利用直线电机对被测试系统进行力加载，其输出能力较弱，如果要求输出较大的加载力，则需要更换更大功率的伺服电机，因而成本较高且无法灵活地满足系列多型号伺服作动器系统的加载测试需求.文献[5]中的加载系统利用弹性杆传递力矩，可以在一定程度上减小多余力矩，但同时也引入了难以区分的结构因素，因而建立精确的加载系统数学模型具有一定的难度.

本文针对合作单位系列多型号伺服作动器的动态性能测试项目与指标要求，采用具有高动态特性的直线电机驱动增力模块实现对伺服作动器的动态加载.本文为加载系统设计了多闭环控制策略，即外环为力闭环，内环为由位置环、速度环和电流环组成的多闭环结构，因而可以提高加载系统的力控制精度.基于力前馈与速度前馈控制解决了系统相位滞后问题，同时基于结构不变性原理对伺服作动器的位移输出信号进行了前馈补偿，从而抑制加载过程中伺服作动器系统位置闭环控制对加载系统进行强位置干扰而产生的多余力.为了更加真实、准确地反映加载系统特性并控制方案的有效性，基于MATLAB/Simulink建立了加载系统的直线电机模型，设计了加载系统的控制方案，同时基于AMESim建立了增力模块与伺服作动器液压系统的仿真模型.为了便于发挥两款软件在各自领域的优势，通过接口技术对加载系统进行了AMESim/Simulink联合仿真试验[6].

1　加载系统结构

本文提出的动态加载系统结构原理如图1所示.该动态加载系统主要包括直线电机、伺服驱动器、增力模块、力传感器、位移传感器、运动控制器与工作台等.利用动态特性和直线加速性能较好的直线电机驱动增力模块，从而对伺服作动器进行小位移、大推力与高频率的动态加载控制.

图1　动态加载系统结构原理图Fig.1　Principle diagram of dynamic loading system

在动态加载过程中由运动控制器产生加载力指令信号，通过直线电机驱动增力模块，从而将力控制信号放大后作用于伺服作动器.增力模块由活塞面积较小的双出杆液压缸1和活塞面积较大的双出杆液压缸2串联组成，选用不同活塞面积的液压缸能够提升系统的驱动力，从而满足不同的加载测试需求.力传感器可以检测伺服作动器实际受到的加载力，并将其反馈至运动控制模块以便实现加载系统的力闭环控制.将两个位移传感器固定于工作台的绝对位置，从而测量加载过程中增力模块与作动器系统输出的位移.

2　加载系统联合仿真模型

2.1　直线电机MATLAB/Simulink模型

在不考虑磁路饱和并忽略端部效应的前提下，采用id=0的永磁同步直线电机磁场定向控制策略[5].根据直线电机d-q轴模型的运动学方程和电压平衡方程，基于MATLAB/Simulink建立了直线电机的仿真模型，具体结果如图2所示.

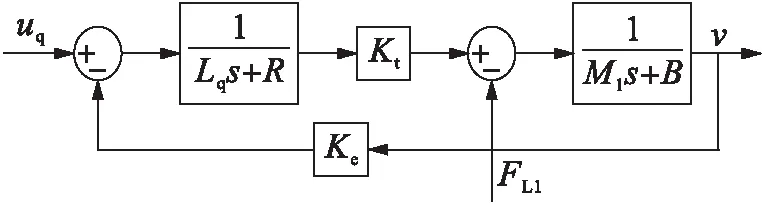
图2　直线电机模型Fig.2　Model for linear motor

图2中v为直线电机动子线速度；B为粘滞摩擦系数；FL1为直线电机受到的外部负载力；uq为q轴电压；Lq为q轴电感；R为每相绕组电阻；Ke为反电动势常数；Kt为推力常数；M1为直线电机动子部分和液压缸1活塞杆的质量之和.本文选用科尔摩根IC44-200型直线电机，其相关参数为Kt=406，Ke=332，R=6.4 Ω，Lq=63.3 mH.

2.2　AMESim模型的建立

AMESim软件作为当今领先的高级工程系统仿真软件，为流体和控制等工程系统提供了完善的仿真环境和灵活的解决方案，并可提供与其他仿真软件之间的丰富接口[7].液压系统是一种非线性时滞系统，对外界环境比较敏感.为了更加真实地反映加载系统的工作环境及系统特性，本文借助AMESim软件建立增力模块及伺服作动器液压系统的仿真模型，通过联合仿真分析可以在设计过程中预测系统性能，从而对该系统进行更深入的了解，以便及早发现系统所存在的薄弱环节并加以消除[8].

2.2.1增力模块AMESim模型

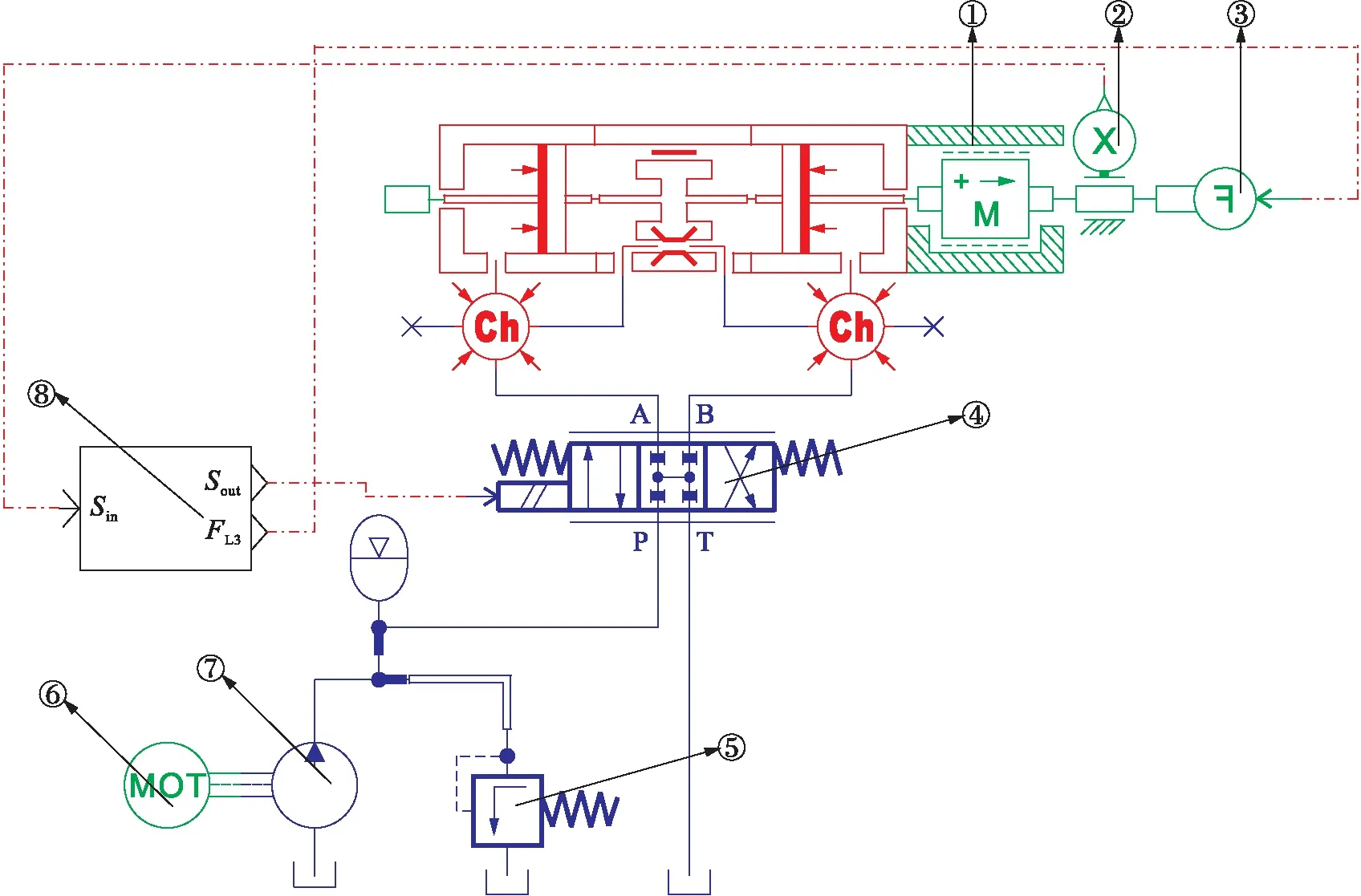
利用AMESim软件建立的增力模块液压系统模型如图3所示.增力模块作为加载系统中的能量传输与转换环节，主要由液压缸1和液压缸2串联组成，单向阀可以避免系统产生负压，溢流阀能够起到保护系统的作用.增力模块将加载系统中直线电机传递过来的机械能转换为双出杆液压缸1的液压能，随后液压能经过油液传递到双出杆液压缸2，之后再将液压能转换成活塞杆运动的机械能.可以通过更换液压缸改变力的放大倍数，使得加载系统灵活地适应不同加载需求的情形.

①、⑥油腔　②、⑤活塞杆　③、④活塞　⑦力传感器　⑧速度发生器　⑨接口模块 ⑩力发生器　位移传感器　质量块　安全阀　单向阀　蓄能器

为了实现与Simulink的联合仿真，需要设置两个仿真软件之间的接口.图3中接口模块表示利用AMESim软件的Interface模块将增力模块液压系统以非线性被控对象的形式输入到MATLAB/Simulink中，并在Simulink模型中以S函数的形式表示.接口模块中FL2为液压缸2活塞杆受到的外部负载力.

2.2.2伺服作动器系统AMESim模型

伺服作动器系统采用阀控非对称液压缸驱动模式，仿照增力模块液压系统的建模方法，利用AMESim软件中的液压库与信号库建立伺服作动器液压系统模型，具体结果如图4所示.图4中质量块表示移动的活塞杆，并通过质量块左右两端的行程来设置液压缸的行程[9].图4的接口模块中Sin为伺服作动器系统的位移指令信号；FL3为伺服缸受到的外部负载力；Sout为作动器系统控制器的输出信号.确定伺服作动器液压系统的关键仿真参数为D3(伺服缸直径)=24 mm，d3(伺服缸活塞杆直径)=16 mm，L3(液压缸行程)=500 mm.

2.2.3加载系统联合仿真模型

在AMESim软件中对已建立的增力模块和伺服作动器液压系统模型分别进行参数设置与编译，然后在Simulink仿真环境中添加S函数，并分别命名为“ZLMKModel_”与“ZDQModel_”，该名称必须与相应的AMESim模型名称一致且必须加下划线，得到的系统联合仿真模型如图5所示.其中：C为力传感器刚度；Fin与Fout分别为输入力和输出力；xin与xout分别为输入位移和输出位移；Ki为电流反馈系数；Kf和Kv分别为力前馈和速度前馈系数，且分别包含一个力指令到位置指令和速度指令的隐式转换.

①质量块　②位移传感器　③力发生器　④电磁阀　⑤安全阀　⑥电机　⑦液压泵　⑧接口模块

图5　系统联合仿真模型Fig.5　Co-simulation model for system

3　控制策略及仿真

3.1　多余力抑制策略与仿真

在对伺服作动器系统进行动态加载过程中，伺服作动器系统受到加载系统施加的力信号，同时因其本身处于位置闭环状态，因而会对加载系统产生强位置干扰，从而导致多余力的产生.力加载系统与伺服作动器系统共同组成一个双输入双输出系统，上述两个系统相互耦合并相互影响，属于典型的双向耦合系统[10].只要伺服作动器进行运动，多余力的产生就不可避免，因而会对加载系统的性能造成很大影响.当对伺服作动器的刚度特性和负载特性进行测试时，力加载系统为主回路；从加载系统的力控制信号输入到加载力输出为主回路通道，该通道体现了加载系统的力控制特性；从伺服作动器的位移输出到加载系统的力输出为多余力通道，该通道体现了加载系统的多余力扰动特性.多余力的存在严重影响了加载系统的性能和控制精度，因此，若要对伺服作动器系统进行高精度的力加载必须有效减小甚至消除多余力.

根据结构不变性理论，可对伺服作动器系统的位移输出进行前馈补偿，从而抑制多余力.结构不变性原理如图6所示.其中：R(s)为指令信号；Y(s)为系统输出信号；s1(s)为可测量的外部扰动信号；G1(s)和G2(s)为系统前向通道的两个不同传递函数；Gw(s)为前馈补偿通道传递函数.

图6　结构不变性原理Fig.6　Structural invariance principle

系统在外部干扰下的系统输出信号表达式为

(1)

为了完全补偿由外部干扰对系统产生的影响，必须满足

(2)

鉴于此，本文利用位移传感器测量伺服作动器系统因位置闭环控制而输出的位移信号，并对该位移信号进行前馈补偿从而抑制多余力.由于前馈补偿对干扰的补偿属于开环控制，因而不会影响原有系统的稳定性.在将增力模块近似为比例环节的基础上，借助MATLAB/Simulink设计加载系统的前馈补偿控制器，考虑到物理上的实现，需要串联滤波环节实现近似补偿.

在完成前馈补偿控制器的设计后进行仿真试验.令加载系统输入的力控制信号为零，伺服作动器位移指令信号频率为8 Hz，正弦信号幅值为0.5 mm，基于相应的系统控制方案，得到添加前馈补偿控制器前后的多余力曲线，结果如图7所示.

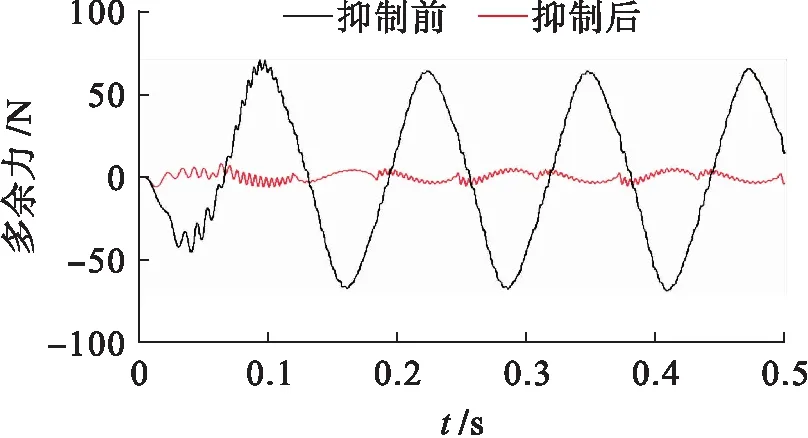
图7　抑制前后多余力曲线Fig.7　　　　Curves of surplus force before and after suppression

由图7可知，添加前馈补偿控制器对多余力进行抑制后，多余力幅值大幅降低，表明基于结构不变性原理的前馈补偿控制策略能够有效抑制大部分多余力，从而可以提高加载系统的力控制精度.

3.2　加载力跟踪策略与仿真

为了提高动态加载力的跟踪性能，本文采用多闭环与前馈复合控制策略.图5中加载系统外环为力闭环，内环为多闭环控制结构，该种结构可以减小力加载的稳态误差.基于力前馈与速度前馈控制，可使系统的输出信号能够快速地跟踪输入信号，减小系统相位滞后，提高控制精度.

通过选用合适的液压缸，可使加载系统中增力模块力的放大倍数为3倍.令伺服作动器系统处于位置闭环状态且位移输入信号为零，给定加载系统的输入力为正弦信号指令力，其频率为5 Hz，输出推力幅值为20 kN，通过仿真得到正弦力跟踪曲线，结果如图8所示.由图8可见，加载系统的实际输出力能够较好地跟踪期望输出力，基本无相位滞后，力跟踪误差较小.

逐渐提高正弦力的输入频率，得到当频率为50 Hz、输出推力幅值为5 kN时，加载系统的正弦力跟踪曲线，具体结果如图9所示.

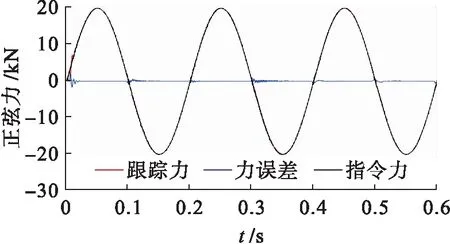
图8　频率为5 Hz、幅值为20 kN的正弦力跟踪曲线Fig.8　　　　Tracking curves of sinusoidal force with frequency of 5 Hz and amplitude of 20 kN

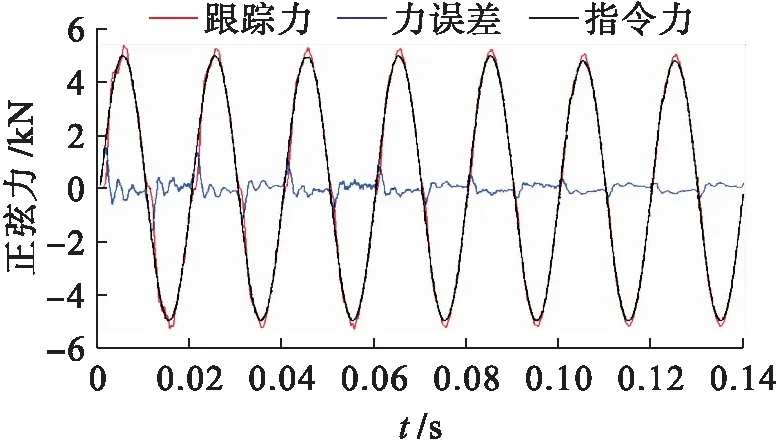
图9　频率为50 Hz、幅值为5 kN的正弦力跟踪曲线Fig.9　　　　Tracking curves of sinusoidal force with frequency of 50 Hz and amplitude of 5 kN

由图9可见，加载系统的相位滞后较小，正弦力跟踪误差呈现周期性稳定存在的状态，但这并不影响加载系统的整体性能.

3.3　系列作动器加载适应性仿真分析

根据应用需求，加载系统应满足不同型号系列伺服作动器的加载试验.为了满足大功率伺服作动器的动态加载测试需要，可以更换增力模块的液压缸.将增力模块的力放大倍数提升至14倍，当正弦力频率为5 Hz且加载系统输出推力幅值为100 kN时，得到的正弦力跟踪曲线如图10所示.

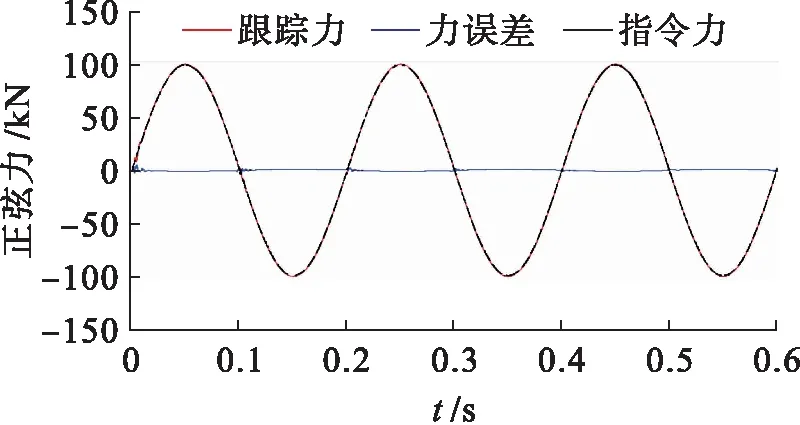
图10　频率为5 Hz、幅值为100 kN的正弦力跟踪曲线Fig.10　　　　Tracking curves of sinusoidal force with frequency of 5 Hz and amplitude of 100 kN

针对小功率伺服作动器的动态加载测试需求，更换增力模块的液压缸，将增力模块的力放大倍数减小至1.5倍，通过仿真试验得到当频率为70 Hz、输出推力幅值为100 N时的正弦力跟踪曲线，结果如图11所示.

图11　频率为70 Hz、幅值为100 N的正弦力跟踪曲线Fig.11　　　　Tracking curves of sinusoidal force with frequency of 70 Hz and amplitude of 100 N

结合图10、11可知，两种条件下加载系统的力跟踪误差及相位滞后均较小.通过更换增力模块的液压缸可以提高增力模块的放大倍数，从而提升加载系统的驱动力；而减小增力模块的放大倍数可以提高加载频率.对于不同型号系列伺服作动器而言，该加载系统可以灵活地满足不同载荷、不同频率的加载测试需求，具有良好的适用性.

4　结　论

通过以上试验分析可以得到如下结论：

1) 相比传统数学建模方法，联合仿真分析方法能够更真实地反映系统特性，仿真准确度更高.

2) 联合仿真结果表明，本文控制方案能够有效抑制多余力，减小系统相位滞后，并提高加载系统的力控制精度.

3) 本文提出的加载系统能够灵活地进行系列多型号伺服作动器系统的动态加载测试.通过更换增力模块的液压缸，可以方便地调整增力模块的放大倍数，从而满足不同的加载试验需求.增大增力模块的放大倍数，可以提升加载系统的驱动力；减小增力模块的放大倍数，可以提高加载频率.