跃出“舒适区”，创造学习场，提升学习力

王江

【摘 要】复习铺垫、创设情境、新知探索、巩固练习……这是教师熟悉的“舒适区”。当下的课堂需凸显儿童的主体地位，构建促进儿童自主学习的“学术课堂”，使儿童获得发展。这就需要教师跃出“舒适区”，走进转型后的课堂，继而激发儿童的深度学习力。因此，对于转型后的课堂，教师从“数学经验”“知识结构化”“素养本位”等角度展开实践与思考。

【关键词】数学经验；结构化；素养本位；课堂转型

不难发现，以前的课堂： 复习铺垫、创设情境、新知探索、巩固练习……教师对每个环节的每句话，都了然于胸，可这样的课堂，看不见儿童，也丢失了“数学味”。课堂正在转型，鲜明地转向“有儿童”的数学课堂，教师真正站在儿童的立场来教数学，这就需要教师跃出“舒适区”，继而真正激发儿童的深度学习力。课前的“研学”“先学”等是课堂转型的重要一环，它是教师理解儿童，准确把握儿童起点的重要手段。唯有理解儿童，知道他们究竟“在哪里”“往哪里去”，在求知的路上，困难在哪里？如此，儿童才能得到发展。

以苏教版六上58页“分数除以分数”一课为例，笔者在课前布置了课前研究单。

【我来研究】

同学们，下面的这道算式，你能正确计算吗？把你的思考和计算过程记录下来。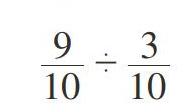

不难发现，六年级学生对于此题，有着多种计算方法，转化小数、画图、倒数……绝大部分能够正确计算，真正存在问题的，只是有些学生的书写不够规范，此外，还有部分学生是基于之前学过的整数除以分数、分数除以整数展开的并不严密的“猜想”。因此，笔者着力以这样的理念展开：儿童能够在小组内自主构建的内容，教师仅仅是“穿针引线”，不多介入，将更多时间用于带着儿童从“猜想”走向“验证”，找到方法之间的联系，经历探索过程。这样的课堂教学，教师需要逐步转型。

一、把握儿童知识起点，从“经而无验”走向“经而有验”

每一个儿童走进教室，或多或少带着经验而来，这会让老师感到“不舒适”，一个知识还没教，学生大部分已经会了，课堂上也并不想听！ 但是“经历了≠获得了”，学生必须实现“活动的内化”，这样才能从“经历”走向“经验”。

数学教学，教师要结合具体的教学内容，精准把握儿童的起点，精心设计数学活动，让学生在观察、思考、比较、分类、抽象、概括、交流和总结等活动中获得感悟和体验，进而深刻理解数学知识的精神实质，积累数学活动的经验。

【片段1】

师：你有什么想说的？

生：离我们的猜测又更近一步了。

师：什么猜测？

生：分数除以分数，就是乘上除数的倒数。（学生鼓掌）

毋庸置疑，数学活动经验需要在“做”的过程与“思考”的过程中积淀，在参与数学学习活动过程中逐步积累。笔者并没有简单告知学生分数除法怎么计算，那无疑是“牵牛上树”，而是巧抓学生的学习起点——“分数除以整数”“整数除以分数”的计算经验。笔者通过查阅学生的课前研究单，发现不少学生是把相关的计算方法迁移到了本节课，还有学生是转化成小数来计算，学生在碰撞、交流的过程中，自然而然积累了转化、迁移的经验，而这些经验，对后续学习有着积极的促进作用。

不仅如此，笔者更是重视数学思想的挖掘与渗透，当学生用一个例子、一类例子就得出结论的时候，笔者追问：“有一点可以肯定，咱们不能凭借这一类例子就下结论。”继而引发学生思维的深度碰撞，不完全归纳法的数学思想也在此时悄然渗透。學生经历了这样的知识形成过程，对分数除法的计算法则理解得更加深刻，在计算、观察、交流和体验中，积累了数学活动经验，同时也感悟了完全归纳法的数学思想。

二、重构儿童数学知识，从“碎片化”走向“结构化”

课前“研学”后，不难想象，儿童将会带着很多的数学知识点来到课堂，倘若我们的课堂仅仅是让学生汇报、交流，而教师不加以引导，那么学生获得的便是“碎片化”的知识点，这同样会让教师感到“不舒适”，因为这些知识点就只能单独地、孤立地存入记忆中，而且将很快被遗忘。因此，教师需要让学生通过自己的努力将知识建立起联系，使知识从“碎片化”走向“结构化”。结构化的数学知识能使学生举一反三，实现数学认知的高级目标。

【片段2】

师出示下图：

生：分母相同，分子能够整除。

师：嗯，这样的分数除以分数，老师赞成这样的方法。不过，同学们有没有想过，究竟为什么分母相同，分子就可以直接除呢？

师：真厉害！一下子就发现了知识的本质。可是，不是所有的分数除以分数，分母都相同啊，怎么办呢？

该片段中，有画图法、整数法、分子直接相除法、字母推导法等，笔者发现这些方法之间都是有联系的，即分母相同，计数单位相同，才有了这些方法。因此，笔者追问：“究竟为什么分母相同，分子就可以直接除呢？”从而引导学生聚焦知识本质：正是因为所含计数单位相同，才有了以上的方法。如此，笔者引领学生打通了刚才这些方法之间的联系，学生的学习自然从“碎片化”走向了“结构化”。

如果教师能够合理把握数学知识的整体框架，并能结构化地设计教学过程，教学就不会沦为“粗暴地给予数学知识碎片”。当我们站在学生的角度帮助他们在学习的过程中边学边“串”，将数学学习整体化，最终学生得到的不仅是数学“知识链”，更多的是数学思维能力、学习能力的提升。

认知结构的重要性不言而喻，而认知结构来源于知识结构，知识结构来源于知识之间的联系、关联、结构化，没有系统全面的数学知识的结构化，也就没有丰富的、联通的、高级的数学认知结构。结构化学习的实践探索，切合了当下数学学习的教学实践探索，也是基于数学学科本质的应然追求。

三、构建儿童深度对话，从“知识本位”走向“素养本位”

传统教学大都是在教师设计好的“支离破碎”的问题链上进行学习的，并且呈现出鲜明的线性方式。在一个个的封闭问题串中，儿童的发散性思维被紧紧地束缚在狭小的空间中。数学教学的价值追求不仅是数学知识与方法的传授，不仅是“做题”“得分”，更重要的是数学素养的培养，因为数学素养是最能体现数学学科独特价值、对学科知识的产生和发展具有重要意义的数学学科精华。

而深度学习是提升学生素养的重要途径，深度学习要求学习者积极地探索、反思和创造，在深刻理解的基础上记忆知识、把握知识之间的联系，并将知识迁移、应用到新的问题情境中，做出决策和解决问题。

【片段3】

生：我觉得不需要这样麻烦，（b÷a） ÷（d÷c）= （b÷a） ÷d×c=（b÷a）×c÷d。运用交换律就可以了。

师：说得挺好，不过这是交换律吗？（学生说是）

师：明白你们的意思，你想表达的是，这里有交换位置的味道，这是你的一种感觉，大家能明白吗？（明白）顺便问问，咱们学过哪些交换律？

生：乘法交换律和加法交换律。用字母表示： a+b=b+a，ab=ba。

生：不过，我还有个补充，这个也可以用字母式子来推算……

的确，笔者可以采用另外一种教学，算理清晰后，通过层层递进的练习，学生做题的正确率可以很高，但这样的教学给孩子留下了什么？如今，我们提倡“素养本位”，既要重视知识技能、思想方法的综合运用，还要重视贯穿数学学习始终的情感态度。

笔者没有止步于简单的结论告知“乘上它的倒数”，而是引导学生思考，进行思维碰撞。于是，字母推导法、方程推导法、商不变规律等方法应运而生，在此过程中笔者引导学生对问题进行积极的思考，并在逐步深入的探究活动中，激活儿童的数学思考，引领儿童经历问题发现、知识发生、思维发展的全过程。

笔者清晰记得在此课教学后的第二天，学生仍沉浸在探究与思考的氛围中，不少学生回家后用字母推导了方程法、商不变规律法。笔者坚信，这些对于学生后续掌握知识前后联系、积累数学思想方法、初中代数演绎等，都有着极其重要的意义。因此，儿童深化理解的不僅是一个简单的知识，还多了一回科学精神理性思考的深度体验。

“素养本位”下的教学，练习也可以从“教师设计”走向“学生设计”。通过一段时间的研究，笔者发现，有些时候学生自己设计的题目，更具意义！如本节课，有学生设计了两个题目（如左下图），问题一中教师可以追问“如果是三角形的面积呢”，问题二更加抽象，也更加聚焦到分数除法的本质：“乘上除数的倒数”。

笔者以为，学生课前研学后，教师对教学内容的把握不应是发散的，而是更应当聚焦。有效的课堂教学并不等同于难度大、范围广、容量大的课堂教学，教师应当基于儿童的起点，把教学的重点聚焦到核心概念的教学上。此外，教师的教学设计不应是微观的，而是宏观的，教师需要跳出一节课的限制，从全局出发把握不同学段的知识之间的联系，形成有利于儿童终身发展的数学教育，如此方能激发儿童的深度学习力。

参考文献：

[1] 高卫杰.从”经历“走向“经验”，以“经验”锻造“精神”[J]. 科学大众，2014（11）.

[2] 翟运胜.促进深度学习，提升数学核心素养[J]. 江苏教育，2016（10）.

[3] 李士锜，吴颖康.数学教学心理学[M].上海：华东师范大学出版社，2011.

[4]吴荣安. 为“不完全归纳”上把“安全锁”——对归纳的结论多些数学理解的实践[J]. 现代中小学教育，2011（2）.

（江苏省南京市玄武区北京东路小学阳光分校210042）