由Apollonius圆引出的一个轨迹问题及其对偶

吴　波　向　霞

(重庆市长寿龙溪中学　401249)

1　由Apollonius圆引出的轨迹问题

定义1[1]如图1，到平面上两定点A、B的距离之比为定值λ(λ≠1)的动点P的轨迹是一个圆，此圆叫做Apollonius圆．

若λ=1，此轨迹是线段AB的垂直平分线．如将直线看作是半径为无穷大的圆，也可以允许λ=1.

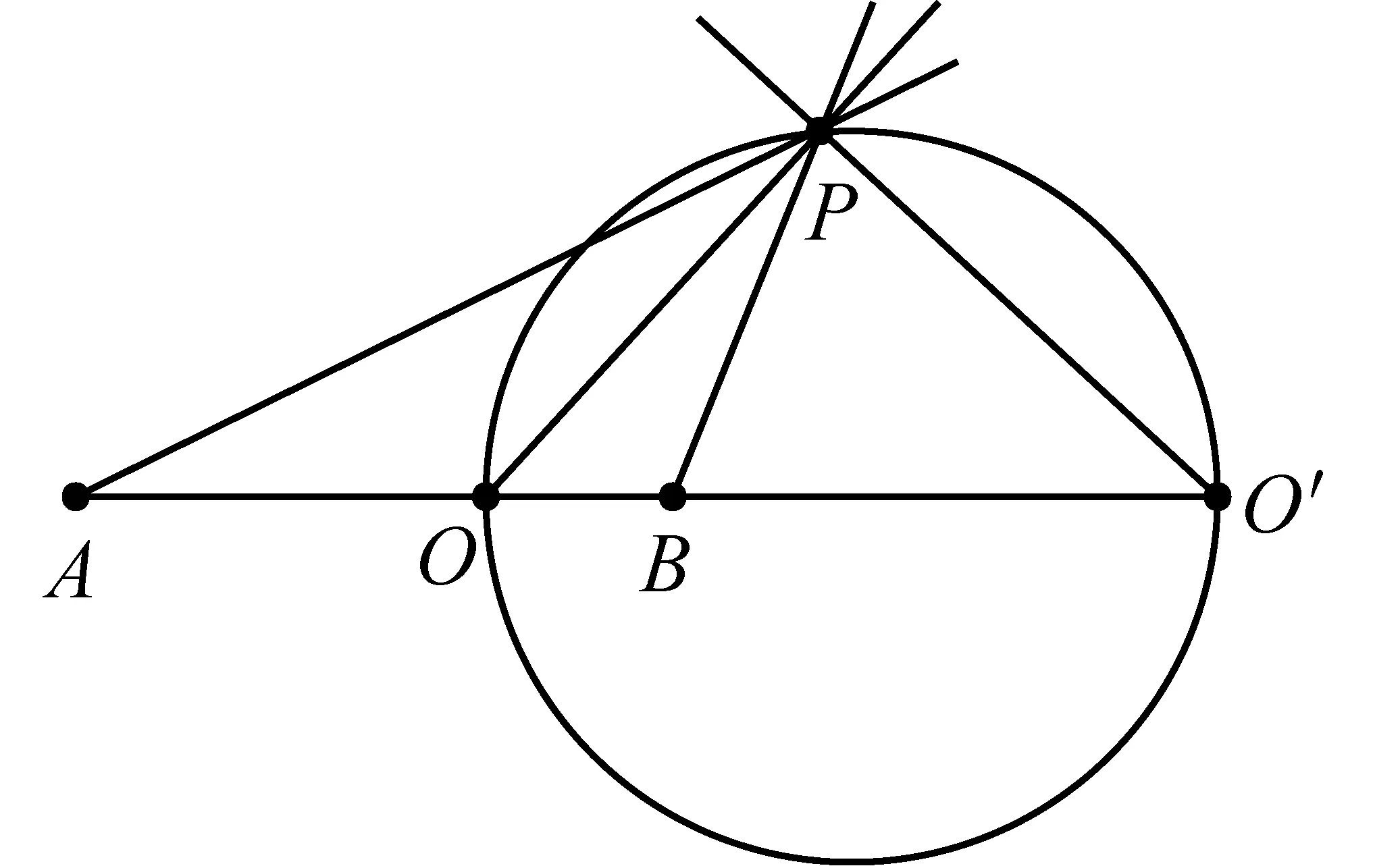
图1

Apollonius圆在高考和自主招生考试中都曾出现，已经有很多文章讨论过它的应用．而我们则注意到如下事实：

如图1，由定义1所确定的Apollonius圆交直线AB于点O、O′，则对圆上的动点P有：|PA|∶|PB|=|OA|∶|OB|=λ，从而PO平分∠APB．同理有：PO′平分∠APB的邻补角.

由此我们想到：能否将定义1中的轨迹改为如下表述形式呢?

如图1，A、B、O(或O′)为共线的三定点．求使得直线PA、PB关于直线PO(或PO′)对称的动点P的轨迹 (约定：动点P取A、B、O(或O′)时也符合条件)．

不过，稍加分析就可发现：按上面这种形式表述的轨迹与定义1中的并不相同．因为除Apollonius圆上的点外，新形式表述中的轨迹还包含直线AB上的点．

但按这种新的方式重新表述之后，若A、B、O为平面上的任意三个定点，则引出如下问题：

问题1设A、B、O为平面上的三个定点．求使得直线PA、PB关于直线PO对称的动点P的轨迹．

本文拟解决这个问题并探讨与其对偶的问题．

2　分析与作图

如图2，对平面上三定点A、B、O，假设点P满足问题1条件“直线PA、PB关于直线PO对称”．作点A关于直线PO的对称点A′，则A′在直线PB上．反过来，点P是直线BA′与直线PO的交点．

由此，我们就可以作出点P的轨迹．具体地说，作法如下：

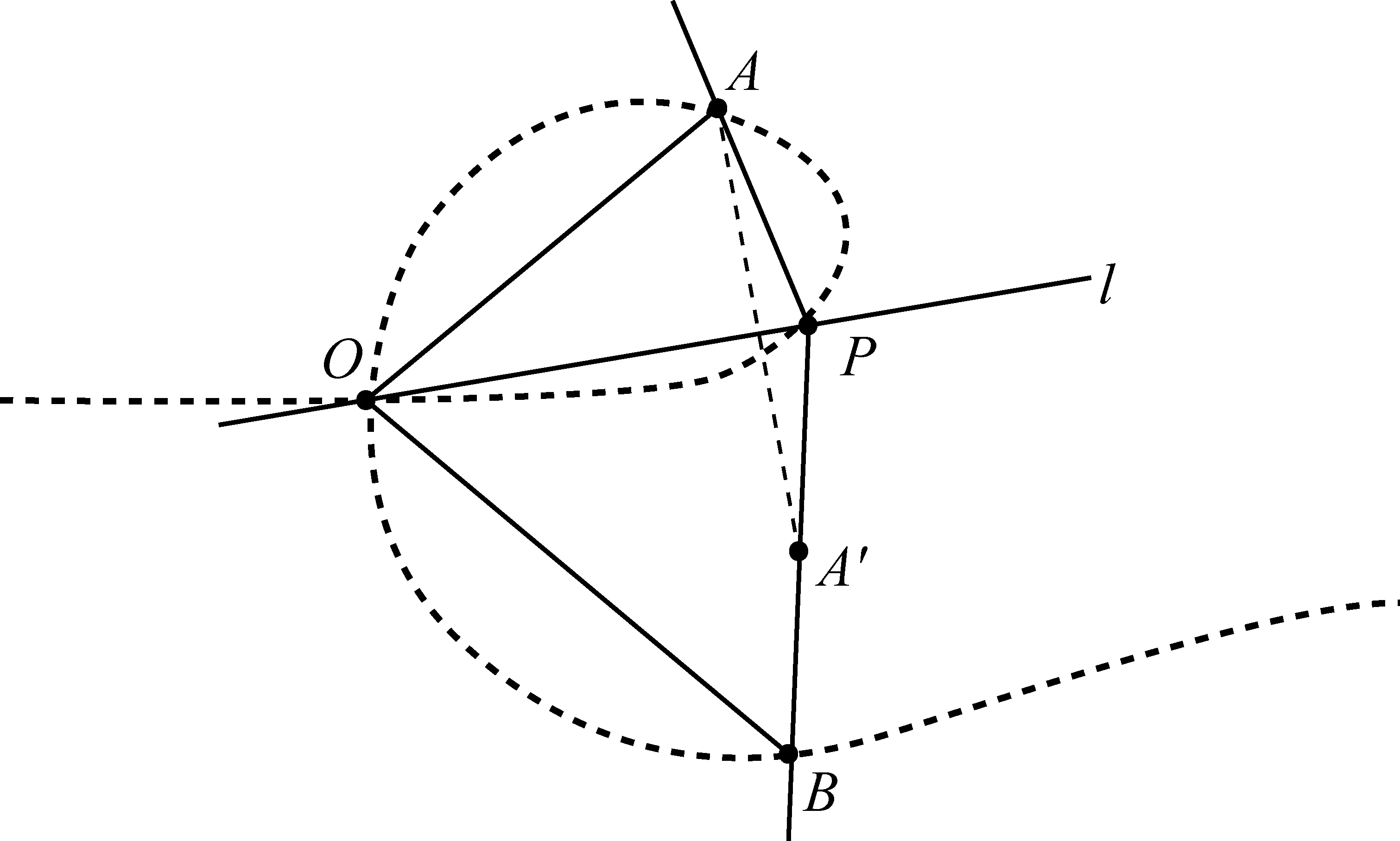
图2

步骤1如图2，过点O任作一直线l．作点A关于直线l的对称点A′．

步骤2作直线BA′，直线BA′与l相交于点P.

步骤3让直线l绕点O旋转，即可得动点P的轨迹．

当三定点A、B、O的位置关系如图2所示时，点P的轨迹曲线有一个结点O，曲线的形状非常像字母“e”．

如图2，当动直线l经过定点A时，A与A′重合．直线BA′是确定的，它与直线l的交点P即是A，因此直线PA无法确定．当动直线l经过定点B时直线PB无法确定．类似地，当P与O重合时，直线PO无法确定．

对上述三种情形，如图2，为保证轨迹曲线的完整性，对问题1我们补充约定：当动点P取A、B、O时也符合问题1的条件——即轨迹中含点A、B、O．

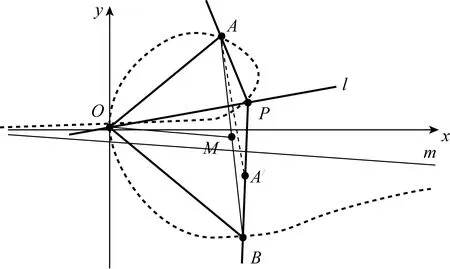
图3

3　轨迹方程

如图3，设│OA│=a，│OB│=b，∠AOB=2θ(其中a,b>0,θ∈[0° ，90° ]且A、B不重合)．

以O为原点，以∠AOB的平分线所在的直线为x轴，其邻补角的平分线所在的直线为y轴建立平面直角坐标系．则A(acosθ,asinθ)，B(bcosθ,-bsinθ).

设绕点O旋转的动直线l的倾斜角为α，则l的方程为xsinα-ycosα=0.

则A关于l的对称点A′的坐标为

(acos (2α-θ),asin (2α-θ)).

则BA′的方程为

(x-bcosθ)(asin (2α-θ)+bsinθ)

=(y+bsinθ)(acos (2α-θ)-bcosθ).

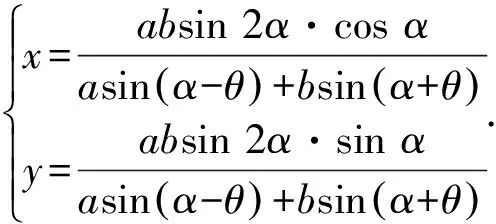
对照组：常规术后护理方法。术后，协助患者进行日常的生活活动，及时观察患者手术部位的伤口愈合恢复情况，指导患者多食用营养丰富的食物等。

下面我们消去其中的参数α．

注意到参数方程中的分母

asin (α-θ)+bsin (α+θ)

=(a+b)sinαcosθ-(a-b)cosαsinθ.

则参数方程中第一式去分母可得

[(a+b)sinαcosθ-(a-b)cosαsinθ]x

=absin 2αcosα．

(1)当α≠90° 时，上式化简为

[(a+b)tanαcosθ-(a-b)sinθ]x=absin 2α．

①

代入①式化简即得

(x2+y2)[x(a-b)sinθ-y(a+b)cosθ]+2abxy

=0.

②

(2)当α=90° 时，由参数方程得P的坐标为(0，0)，仍满足上式．

又，在某些特殊情形下点A′会与B重合，或者直线BA′会与l重合(见下面分析中的第(i)、(iii)、(iv)款)，但易知，这些情形下的轨迹方程仍为②式．

综上，方程②就是点P的轨迹方程．下面对此轨迹方程略作分析．

(i)若θ=0° 且a≠b，即点O在线段AB(或BA)延长线上时，由方程②知此时点P的轨迹方程退化为：直线y=0和圆(a+b)(x2+y2)-2abx=0．前者即直线AB，后者即是Apollonius圆．

(ii)若θ=90° 且a≠b，即点O在线段AB上但不是其中点时，由方程②知点P的轨迹方程退化为：直线x=0和圆(a-b)(x2+y2)+2aby=0．与情形(i)相同：前者即直线AB，后者即是Apollonius圆．

(iii) 当点O是线段AB中点，即a=b且θ=90° 时，由方程②知点P的轨迹方程退化为：xy=0．即轨迹是：直线AB和线段AB的垂直平分线．

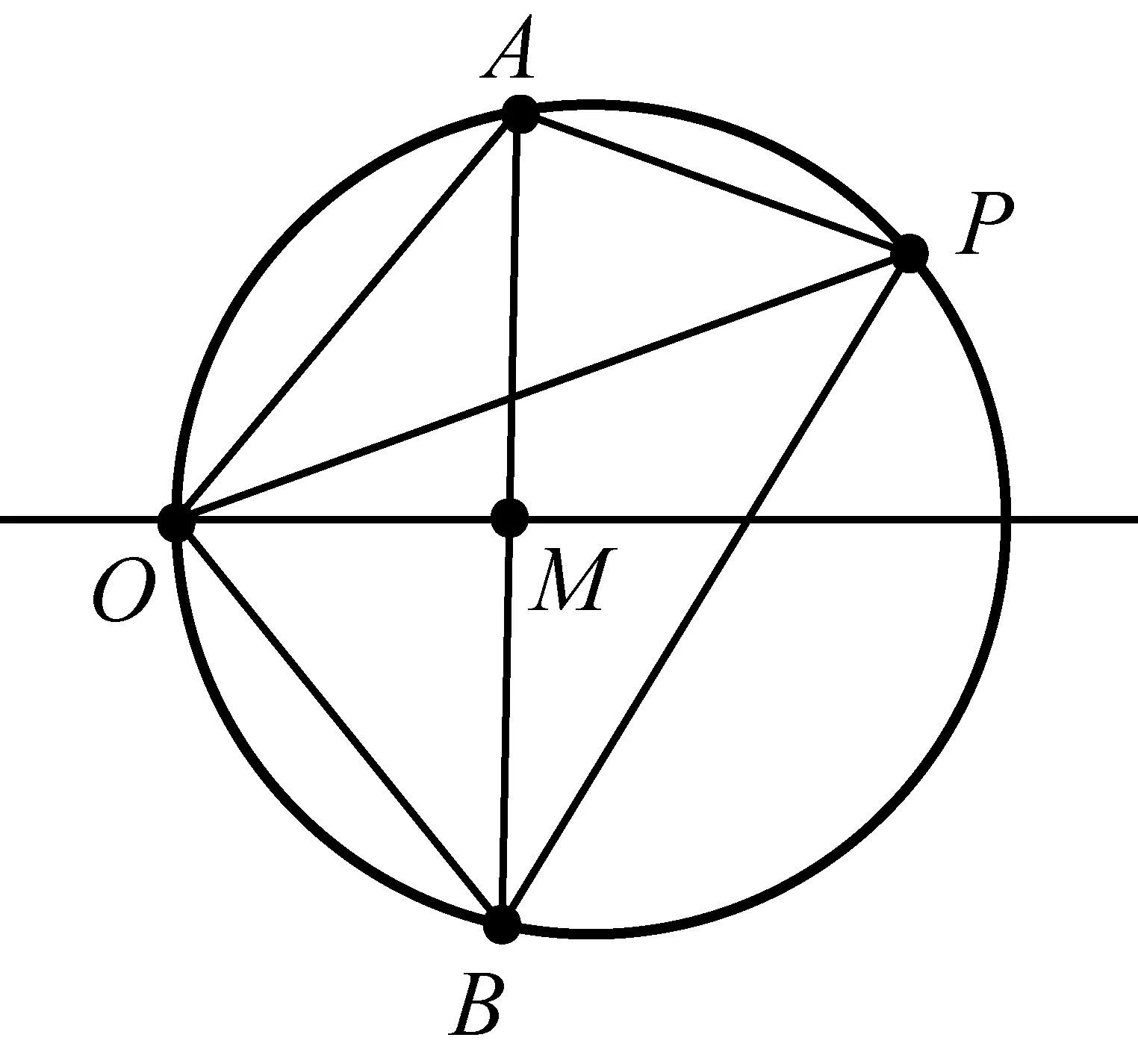
图4

(iv)如图4，三点O、A、B不共线且a=b时，由方程②知点P的轨迹方程退化为：直线y=0和圆(x2+y2)cosθ-ax=0．前者是线段AB的垂直平分线，而后者是△OAB的外接圆.

(v)如图3，当三点O、A、B不共线(即0° <θ<90° )且a≠b时，方程②表明：此时点P的轨迹是一条非退化的三次曲线．可以证明：这条三次曲线有一条渐进线(见图3中的直线m)，其方程为

x(a-b)sinθ-y(a+b)cosθ

如图3，设线段AB的中点为M．易知：渐进线m与直线OM平行．

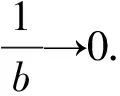
查询了一些相关文献后得知：非退化的三次曲线的分类非常复杂(参看文[2]文[3])．而上面B取无穷远点这种极限情形下的轨迹曲线(x2+y2)(xsinθ+ycosθ)=2axy就是三次曲线中的环索线[4][5][6]．据文[6]所说，环索线也称为“布尔梅斯特(Burmester)曲线”．

对环索线(x2+y2)(xsinθ+ycosθ)=2axy上的点P，仍有“直线PA、PB关于直线PO对称”的性质(只不过因B是无穷远点，作直线PB时要保持固定的倾斜角180° -θ)．值得注意的是：这一性质与文[4]中介绍的环索线的性质1有些相似，但不并相同!

三次曲线虽然是由方程来定义的，但上面的结果表明：这一类三次曲线仍有简单而有趣的几何性质．由此我们想到：

问题2是否还有其它的三次曲线——它们也有着简单而有趣的几何性质？

又，非退化的二次曲线有不少统一的几何性质．但对非退化的三次曲线，似乎鲜有所闻．

4　对偶问题

在问题1中，如将“直线”替换成“点”，将“关于直线对称” 替换成“关于点对称”， 将“动点的轨迹” 替换成“动直线的包络”，我们就想到了与问题1对偶的如下问题(但并非对偶命题!)：

问题3a、b、c为平面上的三条定直线．若动直线l被直线a、b所截得的线段被直线c平分，求动直线l的包络．

注：从包络的完整性角度考虑，我们约定：当动直线l取a、b、c时也符合问题3的条件．

如图5，设a、b、c两两相交的三交点分别为A、B、C(限于篇幅，本文仅研究这种情形)．

假设动直线l被a、b所截得的线段DE被直线c平分，即直线c过DE的中点P．则直线b关于点P对称的直线b′也会过点D．反过来，点D是直线a与b′的交点．而l可由D、P确定．

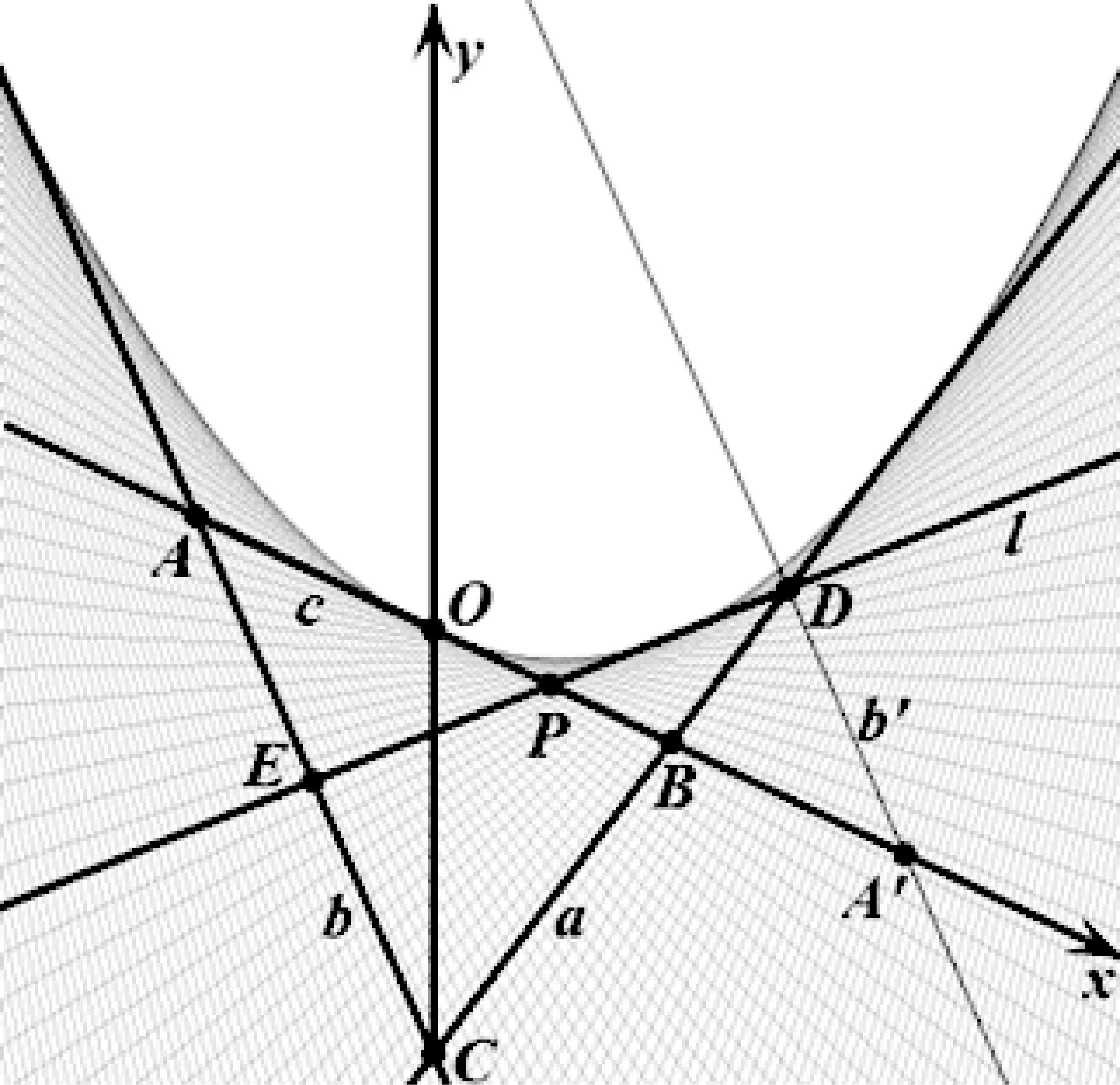
图5

由此，我们就可以作出动直线l的包络．

步骤1在直线c上任取一点P．作直线b关于点P对称的直线b′．直线b′交a于点D．

步骤2过D、P作直线l交直线b于点E．

显然，直线l符合问题3的条件．

步骤3如图5，让点P在直线c上运动即可得到动直线的l的包络．

直观地看，动直线l的包络应该是一条抛物线．下面我们将证明这一点．

定理1平面上三条定直线a、b、c两两相交但不共点．若动直线l被a、b所截得的线段被c平分，则动直线l的包络是一条抛物线．

证明如图5，取线段AB的中点O，作直线OC．设│OC│=m,│AB│=2n.

以O为原点，以直线c为x轴，以直线OC为y轴建立平面斜角坐标系.

则A(-n，0)，B(n，0)，C(0，-m).

则直线a为 -mx+ny+mn=0，

直线b为mx+ny+mn=0.

又设直线c(即x轴)上的动点P为(p，0)，

则点A关于点P的对称点A′为(2p+n，0),

则直线b关于点P对称的直线b′为

mx+ny-2mp-mn=0,

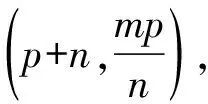
则动直线l(即DP)为mpx-n2y-mp2=0.

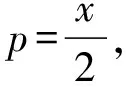
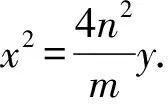
这表明：动直线l的包络为抛物线．证毕．

易知，两点(2kn，k2m)、(-2kn，k2m)都在此抛物线上，则它们的中点(0，k2m)在y轴(即直线OC)上．随着k的变化，以这两点为端点的弦构成抛物线的一组平行弦(平行于x轴，即直线AB)．而二次曲线的一组平行弦的中点轨迹是它的一条直径．这表明：直线OC是此抛物线的一条直径．换个说法即是：这条抛物线的对称轴平行(或重合)于直线OC．

5　定理1的反问题

对定理1,我们还有如下反问题：

问题4对任意一条抛物线，它是否存在三条切线a、b、c，使得对于这条抛物线的异于a、b、c的任意切线l都有：切线l被a、b所截得的线段被c平分?

回答是肯定的．我们可以证明以下定理2.

定理2如图6，直线li切抛物线C于点Pi(i=1,2,3)．P是C上异于P1、P2、P3的任意点．过点P作C的切线l，则直线l被l1、l2所截得的线段被l3平分的充要条件是：由P3和线段P1P2的中点所确定的直线平行(或重合)于抛物线C的对称轴．

证明设抛物线C为x2=2py(p>0)，点P(x0，y0)，Pi(xi，yi)(i=1,2,3).

则切线l的方程为xx0=p(y+y0)，

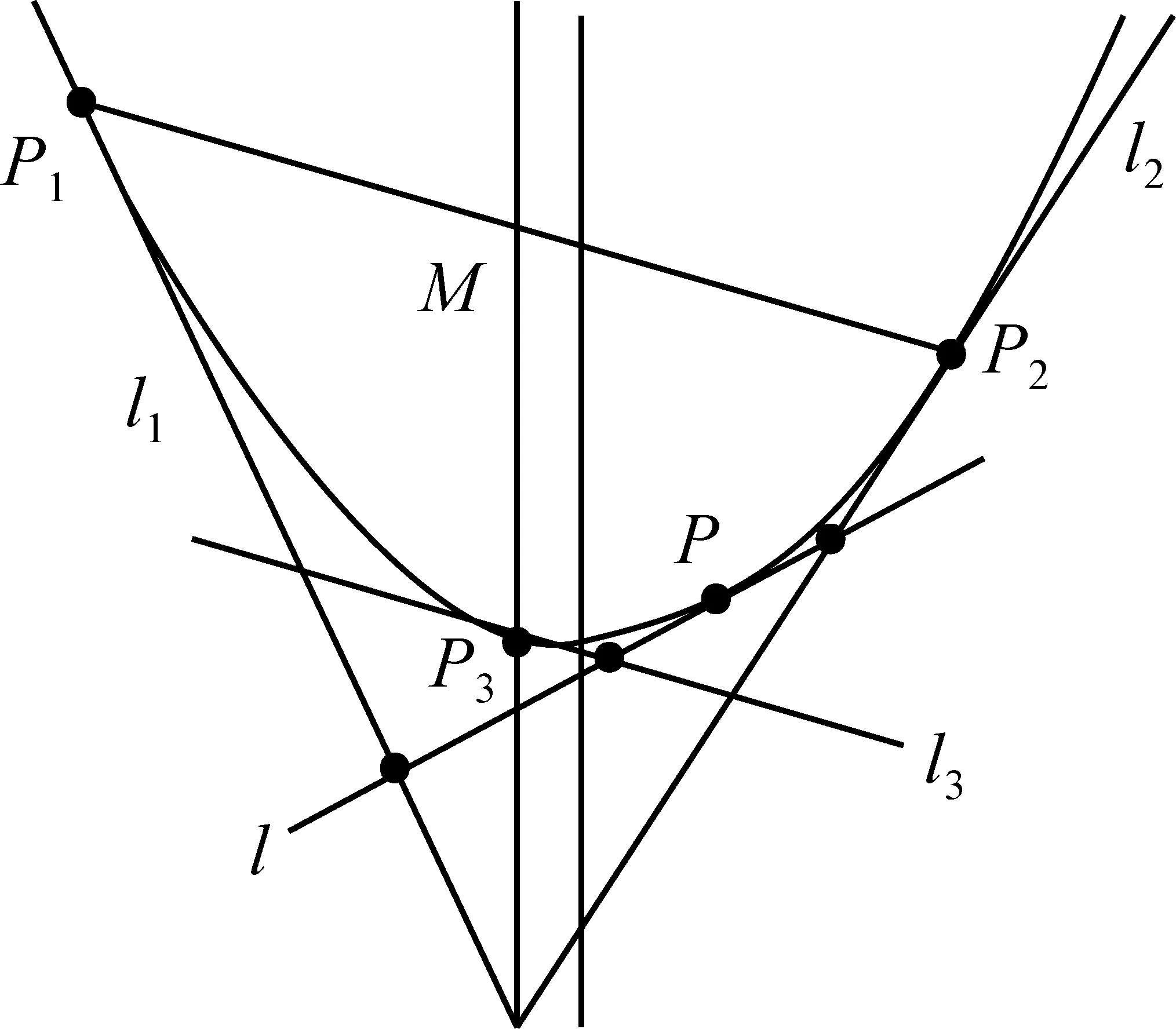
图6

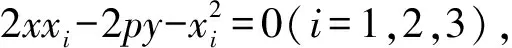
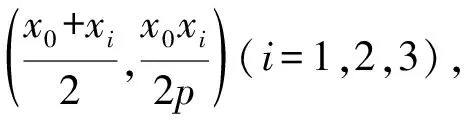
则直线l被l1、l2所截得的线段被l3平分的充要条件是

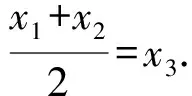
这也即是，由P3和线段P1P2的中点所确定的直线平行(或重合)于y轴 ，即C的对称轴．证毕.