在明暗交织的“问题—互动”教学中培育学生的核心素养 ——以高中“不等关系”教学设计为例

刘权华

(南京市教育科学研究所 210002)

深化课改对我们提出了许多新要求，“为发展核心素养而教”就是其中的一个关键词.人民教育出版社章建跃先生曾撰文说，当下实现学科育人的最关键问题是扎实开展数学教育实践研究，搞出一批“核心素养统领下的数学教学案例”使抽象的高大的“核心素养”获得具体的事例，实现“从思维的抽象发展到思维的具体，在思维中再现事物的整体性和具体性”，这样才能达到对数学核心素养的深刻认识.也就是说，更加迫切的、对实践的指导意义更强的是案例.在数学教学中着意创设一些与数学有密切关联的真实的熟悉的问题情境，从数学知识的发生发展过程，特别是如何发现和提出数学问题，获得数学对象的角度进行实践，是必要的，也是可能的，通过“问题—互动”的方式，可以促进数学教与学方式的转变，有利用于培养学生的模型思想和理性思维，这是新课改的要求，也是数学教学本原的回归.[1]

“不等关系”是苏教版高中数学必修5第三章第一节的教学内容，是“不等式”这章的起始课，教材只给出了可以表示不等关系的3个问题，5道课后练习题，尤其是初中也有“不等关系”这一节内容.如何进行设计，才能上出“味道”，达到培育学生核心素养的目的？

1　教学设想

(1)课标理解：通过具体问题情境，感受在现实世界和日常生活中存在着大量的数量关系，了解不等式(组)的实际背景.让学生感受不等式的意义，是重要的教学目标.虽然不等关系大量存在于现实生活中，但要从中概括出不等式的概念，深化理解不等式的意义，达到学生的心理认可，可能并不是一蹴而就的.

(2)教材分析：本节是章节起始课，对后继的一元二次不等式、二元一次不等式(组)表示的二平面区域、简单的线性规划问题以及基本不等式的证明等学习内容具有基础性的奠基作用，不可等闲带过.其重点是通过具体情境，建立不等式模型，对许多学生来说，这往往也是学习的难点.而要解决这个难点，必须要引导学生对问题中包含的数量关系进行认真、细致的分析，找出其中的不等关系，并由此建立不等式.教材中给出的三个问题，其数学模型为一元一次不等式，一元二次不等式，和线性规划问题.按照考纲要求，本节对问题的研究，只要求建立数学模型，而不要求解不等式.

(3)学情分析：初中有过同样的章节，对“没有内容”的章首课，学生往往不屑一顾.

(4)教学目标：通过具体问题情境，感悟不等式是研究实际问题的重要数学模型；了解不等式(组)的实际背景，会根据实际问题列出不等式，并解决一些简单问题；经历由实际问题建立数学模型的过程，体会其基本方法，培育数学核心素养.

如何通过他们熟悉的生活环境创生出不一样的问题，并通过巧妙的构思，鲜活的实例，合作互动的形式来吸引他们，我尝试以教材为基础，通过明暗两条线交织，并以问题—互动的形式来实施教学.

2　教学设计

2.1　创设情境，感受不等

话题引入秉承“承恩施善，德贯全程，敢当大任，回归社会”的江苏地铁自2005年南京首条地铁——南京地铁1号线开通运营以来，为同学们的出行提供了很多便利和人文关怀，截止2017年2月，南京已有7条线路，地铁建设创造了全国地铁建设的多个记录：

(1)地铁建设速度远远超过世界平均建设速度；

(2)票价低于国内其它城市；

(3)参与建设的工人人数控制在1200人以内……

在这里，建设速度的快慢、票价的高低、人数的多少……都反映了我们生活中的一种常见现象——不等关系.

设计意图创设真实问题情境，使学生感受生活中处处有数学，突出知识产生的背景及其与现实的联系，尝试用数学的语言描述生活中的现象，着意人文底蕴、健康生活、责任担当及数学核心素养之一的“数据分析”意识的培育.

问题1表示不等关系的有哪些句子？其含义是什么？

问题提出后，让学生集思广益，广泛发言，教师适时适切引导、追问，及时互动(下同)

设计意图地铁明线初显，熟悉的情境趣引“不等”话题(暗线).

问题2你能举出一些实际生活中蕴含不等关系或不等式的例子吗？

追问：对于生活中的不等关系，应该如何用数学式子来刻画呢？

设计意图让学生感受不等，揭示学习与研究的必要性，引出课题.

2.2　师生互动，表示不等

问题3如何表示不等关系呢？

根据学生的回答，启发出“用不等式来表示不等关系”.根据学生的回答，追问：什么是不等式？有哪些不等符号？帮助学生回忆出“用不等号(<、>、≠、≤、≥)表示的式子，叫不等式”.

进一步追问：不等号是哪一年发明的？谁首先使用的？

数学史料“不等号”由英国数学家哈里奥特于1631年开始使用，但当时并没有被数学界所接受，直到100年以后，才逐渐成为标准的符号.

设计意图介绍数学故事，不失时机地对学生进行数学史教育.

问题4你能举出数学上不等关系的实例吗？

提示引导：并转化为数学符号语言表达

(1)三角形两边之和大于第三边(a+b>c，a+c>b，b+c>a)；

(2)完全平方数不小于零，(a2≥0)等.

设计意图把学生的思维从日常生活中拉到数学内部.

教师及时补充实例，PPT显示如下内容：

南京地铁4号线运营后，南京地铁轨道线网将突破260公里；

南京地铁3号线的票价介于1.9至8元之间；

根据规定，乘客携带的物品重量不得超过15千克，体积不得大于0.15立方米.

问题5能用不等式表示上述问题中的不等关系吗？

追问：如何将文字语言的不等式转化为符号语言的不等式呢？

启发引导师生共同完成下表：

不等关系词突破介于……之间不超过,不大于不等式S>2601.9≤p≤8{G≤15,v≤0.15

设计意图启发引导找到不等关系，设出未知数，再将找到的不等关系转化为不等式；再显明线，仍用地铁为背景.

2.3　建立模型，应用不等

问：对于较复杂的问题，我们如何用不等式来建立数学模型呢？

例1某位同学为自己制定的月交通费支出总额为120元，若他乘坐地铁一次需要2元，乘坐出租车一次需要15元，问他每月需乘地铁多少次才不会超支？(假设该生每月从家到学校往返共40次)

解设该同学每月乘地铁x次，则他乘坐出租车(40-x)次.

故2x+15(40-x)≤120，(x∈N)

则有13x≥480.

设计意图让学生初步感受“一元一次不等式”模型，例题由教材第一个问题以“地铁”为背景改编而来.再次体现着意设计的“地铁”这条明线，更着意健康生活和数学抽象和模型化等素养的培育，没有求解出不等式，体现课标要求，下同.

问题6你能总结出解决不等关系的实际问题的一般步骤吗？

师生互动，共同得出：

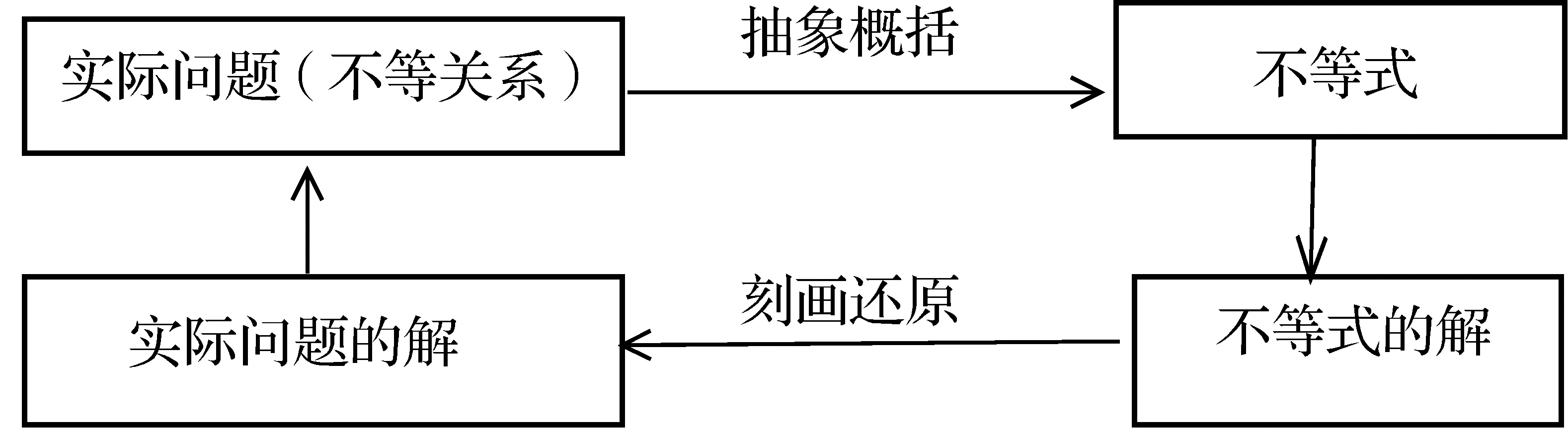
设计意图示以思维之道：用数学的眼光观察客观世界，用数学的思维分析实际问题，用数学的语言表达实际问题，用数学的方式和知识解决实际问题.使学生体会到不等式是研究实际问题的重要数学模型,同时经历由实际问题建立数学模型的过程，体会其基本方法，着意数学抽象和数学建模等核心素养的渗透和培育.

例2地铁站设有多台自动贩卖机出售饮料，若某种饮料以每瓶2元的价格销售时，月销售总量为10万瓶.经过大数据调查，若价格每提高0.2元，销售量就减少5000瓶.问每瓶价格的定价为多少元时，才能使该饮料月销售额超过22.4万元？

解设该饮料的定价提高x元，根据题意得到

(2+x)(10-(5x)/2)>22.4,

化简得5x2—10x+4.8<0.

设计意图用数学的思想分析问题，用数学的语言表达问题，用数学的知识得到模型，题中的数学模型是一元二次不等式，进一步经历由实际问题建立数学模型的过程，深化建模思想.此题源于对教材中第二个问题的改编.

例3在制造地铁列车的过程中，需要把长度为4000mm的钢管截成500mm和600mm两种.按照生产要求，600mm钢管的数量不能超过500mm钢管的3倍，请写出满足上述不等关系的不等式.

解设截成500mm的钢管x根，截成600mm的钢管为y根，则有，

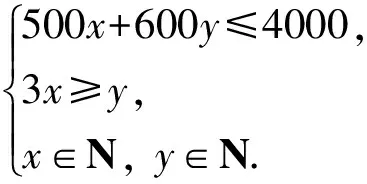
设计意图此题源于对教材中第3个问题的改编.模型是线性规划，表明我们还可以用不等式(组)来刻画不等关系，使学生进一步经历由实际问题建立数学模型的过程，体会其思想和基本方法.

2.4　深入延展　提炼不等

例4在b克糖水中有a克糖，若再加上m克糖(m>0)，则糖水变得更甜，试根据这个事实提炼出一个不等关系.

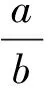
追问：我们用数学知识来诠释生活哲理，生活将变得韵味无穷，在日常生活中，你还能举出这样的例子吗？

启发引导出：女同志为什么喜欢穿高跟鞋？芭蕾演员演出为什么要踮起脚尖(一般人下半身与全身长之比在0.58—0.6之间，穿高跟鞋或踮起脚尖增加了比值，接近0.618)

设计意图题中数学模型是分式不等式，是对学生的数学抽象、建模意识和能力的进一步培育，理性思维的进一步提升.此题源于对教科书习题第5小题的改编，也为学生感受生活中处处有数学，时时有不等关系埋下知识的伏笔.此处没有对提炼的不等式进行证明、变式和甄别(如没有对m的正负,a,b的大小进行深度讨论、分析)是体现课标要求和对学情的尊重.

2.5　深入延展　感悟不等

问题7今天我们是怎样开展对“不等关系”的研究的？

经过师生充分的思考和互动之后，总结如下：我们从引以为傲的南京地铁谈起，从了解地铁、“乘坐”地铁，在地铁站销售饮料、“制造”地铁、“喝过”糖水不等式，这一条明线.另一方面，我们从感受不等开始，学习了如何表示不等、应用不等、提炼不等、感悟不等、回味不等，到最后证明不等的尝试，这是一条暗线.与此同时，还学习和建立了一元一次不等式，一元一次不等式组，一元二次不等式和分式不等式等数学模型……

2.6　总结提高　回味不等

问题8你有哪些收获、体验和感悟？

充分的互动，总结如下：通过本节课的学习，我们感受到生活中处处有数学，时时有数学，正如数学家陈省身所说：我们欣赏数学，我们需要数学.不等是绝对的，相等是相对的，不等关系是数学中最重要的一种关系，我们需要不等关系，我们用好不等关系，就可以用力最省，花钱最少，效益最高.

设计意图言归正传，适当小结，引用名人名言，进行数学史教育，强调等与不等的辩证关系，渗透辩证法思想.同时培养学生的语言表达能力，归纳概括能力，兼顾过程和方法；情感、态度和价值观方面教学目标；教育最终指向全面发展的人.

3　教学反思

让学生身临问题情境，尽量感悟提出、解决问题的真实过程，这是提升数学核心素养的有效途径.以问题引领来激活学生思维是数学课堂教学有力的抓手.有了问题，学生的思维才有了方向与载体、才有交流展示的机会、课堂才能被激活.基于以上认识，本课采用了问题—互动的教学模式，通过设计了8个环环相扣、层层推进的“问题串”，保证了课堂的有序和流畅.但“问题—互动”引领必须要遵循两个原则：一是要连续性原则，即设计的问题要围绕教学主题，连续不断地层次推进，才能保证学生步步为营的持续提高.否则，必将给人神散形也散之感.二是“最近发展区原则”，即设计的问题要来自学生的生活，贴近学生的认知水平和思维水平，必要时搭好“脚手架”，促进不同层次的学生均有所发展.三是要互动原则，即师生互动，生生互动，人机互动，全员互动.这种动不是教师牵着学生鼻子走(所谓“主导”)的动，也不是只有发言同学和少数尖子生的“垄断”的动，更不是看上去热热闹闹(所谓“主体”)实质上是注入式的缺少创新的动，而应是学生发挥主观能动性的自主的动，围绕教师精心设计的有思考价值的问题的交流、合作的动.[2]

“明暗交织”是“问题—互动”教学的一种美好形式.皮亚杰认为：认知发展可分为内化建构和外化建构，学生知识的掌握和能力的发展应该是内化建构和外化建构同时得以发展的过程.本节课教学以两条线展开，暗线是不等关系，从感受不等、表示不等、应用不等、提炼不等、感悟不等、回味不等直到作业布置中的再见不等和证明不等，明线是围绕南京人引以为豪的地铁展开，从选乘地铁、到南京地铁轨道线网、票价、乘客携带的物品重量规定等的地铁背景、乘坐地铁的费用支出(例1)、地铁站自动贩卖机饮料的出售(例2)、直到地铁列车的制造(例3).围绕明线的例题都是来自教材提供的例题或习题，数字没变，背景改动而已，因为主题没变，加上话题也始终是学生熟悉的具体的生活情境，故始终给人以整体感、真实感.或明或暗，明暗交织，使学生注意力思维活跃、敏捷；数学建模及思想方法的体会和运用恰到好处，初步达成了“为实现学生的核心素养而教”，实现了使课堂教学超越知识技能进而使数学核心素养“落地”的初心.[3]