高超声速飞行器非线性巡航控制器设计
赵宏宇, 黄得刚, 何启志, 章卫国
1.兵器工业集团 航空弹药研究院, 黑龙江 哈尔滨 150036;2.西北工业大学 自动化学院, 陕西 西安 710129;3.陕西省飞行控制与仿真技术重点实验室, 陕西 西安 710129
我国著名科学家钱学森于1946年首次提出了高超声速(Ma>5)的概念,能够超过这个速度的飞行器包括导弹、火箭和航天飞机,而在大气层内飞行的飞行器还未能以该速度巡航。从战略侦查的角度来讲,如果侦查飞行器具备了这种高超声速巡航能力,那么其隐身性能将不再重要。速度是新的隐身,为应对未来数十年可能产生的威胁与挑战,提高飞行速度十分必要。正如隐身技术改变今日的战场环境一样,速度将改变未来的战场规则和作战模式。
高超声速飞行条件下,气动热弹性为主要的物理问题[1-4]。气动热弹性现象的存在将会引发飞行器的外形发生变化、机体弹性形变、弹性振动等问题,也引入了动态不确定因素[5],这种现象的存在已经在美国SR-71侦察机上得到了验证[6],另外这种气动热弹性引起的弹性振动是一种极具破坏力的气动弹性不稳定现象,剧烈的震颤将会对飞行器壁板结构的疲劳寿命甚至飞行器的飞行性能产生十分不利的影响,甚至会导致飞行器在短时间内解体[7]。再者,相比于亚声速和超声速飞行器来说,高超声速飞行器在其控制问题上相对复杂[8],原因在于:①以X-43A和X-51A为代表的新一代高超声速飞行器,普遍采用吸气式冲压发动机为高速飞行推进系统的设计方案,研究表明,对于这一类飞行器来说,推进系统与机身之间存在严重的耦合效应;②高超声速飞行器与亚声速/超声速飞行器相比有许多不同的飞行特性,有的方面目前还无法完全掌握,使得高超声速动力学呈现强不确定性。高超声速飞行器的不确定性主要来源于气动特性、气热特性和大气干扰三方面[9-10];③高超声速飞行时,需要对飞行包线进行保护,一旦偏离飞行包线就会出现“热阻现象”,这种热现象显著降低飞行器的整体性能,最直接的方法对航迹角进行高精度控制[11];④随着飞行速度的不断提高,对飞行器的实时性要求越来越苛刻,对于以5马赫速度飞行的飞行器,每延时1 ms,就会产生1.5 m的误差。因此,控制系统的快速性也是一个需要解决的问题[12];⑤目前大量文献中的高超声速飞行器的控制问题一般只考虑纵向控制,如果加上横侧向的控制会使得问题变得更加复杂[13],因此,横侧向的控制对纵向控制的影响需要予以考虑。
对于高超声速飞行器的控制问题,国内外已有不少相应的研究成果,如鲁棒控制[14-16]、Backstepping控制[17-18]、滑模控制[19]、基于优化方法的控制[20]、动态逆控制[21]等,虽然这些先进控制方法都取得了不错的控制效果,但是对于上述给出的高超声速飞行器独有的特性来说,这些控制方法中并没有给予充分的考虑。本文以高超声速飞行器在30 km处以6马赫定速巡航飞行为研究背景,提出一种指令滤波积分动态面backstepping滑模控制方法,该方法首先利用一个二阶指令滤波器解决传统backstepping方法中存在的“计算膨胀”问题;其次,引入滑模控制解决存在匹配不确定性和外界扰动的控制问题,采用带调节函数的自适应backstepping方法来处理存在匹配不确定性的控制问题。为了降低引入滑模控制带来的抖动,本文利用高阶滑模控制的思想,在传统backstepping方法上增加了一个虚拟控制状态方程,将系统的最终输出作用在一个积分器上,从而达到降低滑模抖动的目的。这样所设计的控制器不仅可以解决匹配和非匹配不确定性以及外界扰动的问题,而且还可以降低引入滑模控制带来的抖动;然而引入一个附加虚拟控制方程会导致传统backstepping方法的“复杂性膨胀”问题,即随着系统阶次的增加,控制方法设计过程中的中间虚拟变量导数的计算将会维持不住[22],而动态面方法可以有效解决这一问题[23]。最后,本文从理论上证明了所提方法的全局稳定性,并同时通过仿真实验验证了该方法的鲁棒性和有效性。
1 高超声速飞行器6自由度非线性数学模型
本文采用高超声速飞行器的6自由度非线性模型作为研究对象
(1)

力和力矩的表达式为[16,26,27]
(2)
nA=nmrc+XcgY
i=1,2,3
式中
(3)
j=T,M,L,D
i=1,2,3
相关气动系数具体数值参见文献[7,15-16,18,24,26]。
为了便于实际应用中的控制器设计,需要将(1)式按照纵向和横侧向解耦的形式进行整理变形,可得纵向数学模型为
(4)
式中
fα=-tanβ(pcosα+rsinα)+
gα=1
fγ=
fh=0
gh=V
符号mA(δe)和L(α)表示俯仰力矩和升力的表达式中含有升降舵和迎角变量,可以利用相应的气动关系导出所需的控制变量。同理横侧向的数学模型为
(5)
式中
由于fμ书写过长,此处不在给出,按照(1)式中的倾斜角μ的微分方程可以很容易的导出fμ的具体表达式。另外符号lA(δa)和nA(δr)表示滚转力矩和偏航力矩中含有副翼δa和方向舵δr变量,利用气动特性可以导出相应的控制关系式。同样的方法可以得到发动机推力的数学模型为
(6)
式中
至此,根据(4)~(6)式的形式,很容易实现纵向为h→γ→α→q→δe的控制,横侧向为μ→p→δa和β→r→δr的控制,以及空速为V→Φ的控制。同时根据非线性数学模型的特点,还需要引入各种交叉耦合的影响。下面根据(4)~(6)式来设计6自由度非线性数学模型的控制器。
2 非线性控制器设计
2.1 二阶指令滤波
本文采用二阶backstepping控制方法,这样推导控制律时需要计算期望输入的二阶导数,故这里采用二阶指令滤波。假设滤波器的传递函数如下
(7)
式中,ζ为阻尼比,ωn为滤波器的自然频率,增加ωn可以使得闭环控制系统的解任意精度接近求解解析导数的闭环系统的解[28-29]。
2.2 积分backstepping控制
为了方便说明问题,本文仅以推导最内环的俯仰角速率控制器的设计过程为例,其它控制环的设计过程类似,此处不再赘述。假设俯仰角速率状态变量为x1,实际升降舵控制变量为x2,引入的虚拟控制u,则有
(8)
式中
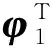
首先定义位置误差为
z1=x1-zd
(9)
式中,zd为状态x1期望的输入指令信号,则
(10)
定义
z2=x2-α1
(11)
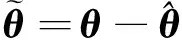
(12)

定义Lyapunov函数
(13)
并定义
(14)
式中,Γ是正定矩阵,V1对时间求导可得
(15)
令
(16)
τ1=φ1z1
(17)
从而可得虚拟控制量α1为
(18)
式中,c1>0,并将α1通过一个一阶滤波器
(19)
这样可以利用(19)式直接得到α1的一阶导数,无需再计算α1的解析一阶导数,因为随着系统阶数增加,α1各阶导数的解析形式十分复杂。
再对(11)式求导可得
(20)

(21)
如果z2=0,则V1≤0,为此需要进行下一步的设计
定义Lyapunov函数
(22)
对V2求导可得
(23)
由此可见,当采用动态面后,推导自适应backstepping方法的第二步时,弹性模态部分也被包含在中间虚拟变量α1中,同样无须计算弹性模态的导数,降低了backstepping方法的复杂性。

(24)

(25)

(26)
整理可得最终的虚拟控制量u为
(27)
从而可得
(28)
由(27)式可见,相比于传统的backstepping方法,所得最终控制律的形式十分简洁。
以上可称为标称系统的控制律设计,可以记为ueq=u,为了保证系统对外界的扰动和匹配不确定性的鲁棒性,设计切换控制律usw为
usw=-εsgn(s)-ks
(29)
式中,s为
s=λ(z1+z2)
(30)
式中,ε>0,k>0,λ>0,sgn(·)为符号函数,从而系统总的输出量为
U=ueq+usw
(31)
将(31)式的结果积分后恰为模型所需的升降舵控制输入x2,该指令滤波积分backstepping滑模控制的结构方框图如图1所示。

图1 指令滤波积分动态面backstepping滑模控制结构图
3 控制器的稳定性分析
为了分析控制器整体的稳定性,首先分析动态面Backstepping控制的稳定性,为此给出如下假设1和定理2。

定理1考虑非线性系统(8),给定非线性特性和不确定性满足假设条件1,则对于任意初始状态,存在面增益系数ci,i=1,2和时间常数ε1使得动态面backstepping控制器能够保证系统状态收敛到原点。
证明略,详细证明过程参见文献[22]。
得到动态面backstepping控制的稳定性之后,需要继续证明指令滤波动态面积分backstepping滑模控制器的稳定性。不失一般性,假设图1中的虚线内为一般非线性控制系统为
(32)
式中,y为实际控制输入经过指令滤波器后的控制量,同时将(7)式指令滤波器转化为状态空间形式

y=hξ,ξ∈Rq,u∈R
(33)


(34)
假设当y=0时,系统(32)在平衡点x=0处全局稳定,且存在Lyapunov函数V(x)满足
(35)
式中,W(x)正定。此时需要解决系统(34)是否为全局稳定的问题,该问题可以转化为镇定系统(33)不影响系统(32)稳定性的问题。
假设2系统(A,b,h)为反馈正实系统,即对于系统(33),存在线性反馈变换u=Kξ+v,使得(A+bK)是Hurwitz的,且存在p>0,Q≥0满足
(A+bK)TP+P(A+bK)=-Q
Pb=hT
(36)
引理设V(x)为系统(32)的Lyapunov函数,且满足式(35)。如果(A,b,h)是反馈正实系统,那么系统(34)的Lyapunov函数为
Va(x,ξ)=V(x)+ξTPξ
(37)
且控制律
(38)

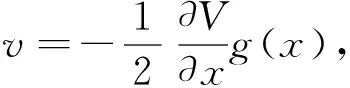
因为Va径向无界,且Va的导数为负半定,故x(t)和ξ(t)全局有界。此外LaSalle定理保证了x(t)和ξ(t)收敛到Ea的最大不变集Ma上。为了说明镇定系统(33)不影响系统(32)的稳定性,首先证明图1中虚线框内的积分动态面backstepping滑模控制器的稳定性。
定理2对于系统(8),采用控制律(31)可以使系统(8)渐近稳定。
证明:根据等效控制理论可知,为使设计的控制律U稳定系统(8),需满足滑模稳定条件[31],则定义Lyapunov函数
(39)
将其对时间t求导可得
(40)
整理可得
(41)
定理3如果y=0时,系统(32)在平衡点x=0处为全局渐近稳定,那么系统(33)在平衡点x=0,ξ=0处也为全局渐近稳定。


定理4如果内回路控制为全局渐近稳定,那么外回路控制亦为全局渐近稳定。
证明假设内回路俯仰角速率控制系统的跟踪误差为eq,针对外回路的迎角控制,需要考虑内回路对外回路的影响,为此选取Lyapunov函数为
(42)

(43)
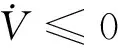
(44)
即内环俯仰角速率若为全局渐近稳定,那么其外环的迎角控制也为全局渐近稳定。由此易知,外环的航迹角控制和高度控制,各个回路均为全局渐近稳定;同理可知,横侧向控制系统亦为全局渐近稳定。至此,证明了所设计的控制系统能够保证高超声速飞行器6自由度非线性数学模型的稳定性。
4 仿真计算验证
临近空间指的是20~100 km的空间范围,本文假设高超声速飞行器以6马赫的速度飞行,飞行高度为30 km,该高度属于平流层,临近空间平流层的气流运动相对稳定,气流以水平运动为主,根据NASA给出的35 km以内的平均风速随高度的变化曲线示意图可知30 km处的风速平均为14 m/s左右[33],故本文利用Matlab中的Dryden风场模型,在高超声速飞行器过程中加入14 m/s的常值风干扰,并将文献[7,14-15,17,21]给出的所有气动数据摄动+20%,以此来验证所提方法的控制效果。
初始条件设定为
x0=[h,V,γ,μ,α,β,p,q,r]=[30 000,5 859.7,0,
0,0.447 88°,-0.1,0,0,-0.082],仿真时间设定为50 s,以高度30 km定高飞行时,6马赫对应的飞行速度为5 859.7 m/s,仿真结果如图2所示。

图2 高度跟踪 图3 高度跟踪误差 图4 速度跟踪
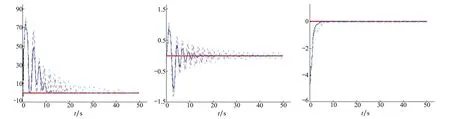
图5 速度跟踪误差 图6 航迹角跟踪 图7 侧滑角跟踪
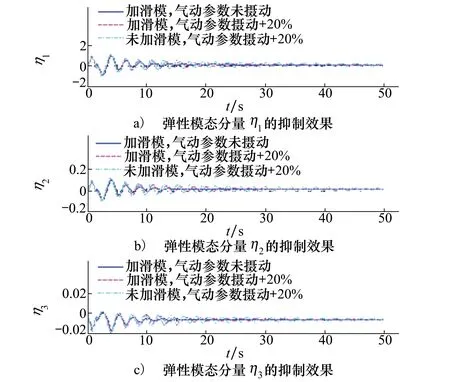
图8 弹性模态的分量

图9 弹性模态分量的叠加 图10 升降舵偏转 图11 燃料当量比
利用文献[16, 24]中给出的气动热引起的弹性振动表达式得到的仿真结果如图8和9所示,图8给出了弹性模态的3个分量,图9给出弹性模态3个分量的叠加结果,将这三者叠加后分别作用在升力、阻力、俯仰力矩和推力力矩上,以此来模拟气动弹性热对高超声速飞行器定速巡航时的影响。根据仿真图8和图9可知,当所有气动参数摄动+20%时(弹性模态参数同样摄动+20%),由于迎角、升降舵和弹性模态之间的耦合影响,使得舵面偏转加剧的同时,弹性模态分量的变化也随之加剧,从而使得叠加后的弹性模态振动加剧,显著影响高度跟踪的精度;从图2~图7的仿真结果可以发现,气动参数未摄动的情况下,高超声速飞行器可以很好实现高度的跟踪、航迹角的跟踪、侧滑角的跟踪和速度的跟踪控制,然而当所有的气动参数摄动+20%之后,去掉滑模控制的控制效果显然要差,这样从实验的角度说明了滑模控制在处理匹配不确定性和外界扰动问题的优越性。然而,即便是所有的气动参数摄动+20%之后,本文所提控制方法能够保证系统的全局稳定性,而且跟踪误差成渐近收敛的趋势。另外,根据图6的实验结果可知,航迹角约在1°范围内进行波动,系统不会出现“热阻现象”。再者,在设定的50s仿真时间内,升降舵的偏转如图10所示,该实验结果表明,在飞行器高超声速飞行时,升降舵的偏转角度在规定的范围内偏转,同时观察图10右下方的小图,该小图表明所设计的控制器没有因为引入了滑模控制而产生抖动现象;值得注意的是在仿真开始时,舵面的调整幅度较大,原因在于气动热弹性模态引起的振动较大,需要利用升降舵的偏转对其进行抑制。而在参数未摄动的情况下,随着气动热弹性振动趋于平稳状态,升降舵的偏转也趋于稳定状态,收敛值约为-4°,而当升降舵偏转角度出在5°偏转角的范围内时,飞行器高超声速飞行的阻力会显著降低[25],适合高超声速飞行;在参数摄动+20%的情况下,升降舵偏角同样可以收敛到5°偏转角的范围内,同样满足高超声速飞行的条件;最后,利用文献[16]中给出的燃料当量比的计算公式,可以得到相应的燃料当量比的仿真结果,如图11所示,根据该仿真结果可知,燃料当量比满足其约束范围。
5 结 论
高超声速飞行器在30 km处以6马赫定速巡航时,不仅存在气动参数的不确定性和外界大气扰动,而且由于高超声速飞行导致的气动热弹性问题较为严重,这种弹性振动对飞行器的稳定性的影响十分显著,处理不好这种弹性振动会使得高超声速飞行器变得不可控,甚至出现飞行器解体的危险,为此,本文提出了一种指令滤波积分动态面backstepping滑模控制器,仿真结果表明,所提出的控制方法不但可以有效地应对引言中提到的高超声速飞行器独有的一些飞行特性问题,而且可以较好地完成高超声速飞行器6马赫定速巡航的飞行任务。

