一类脉冲种群模型渐近概周期解的研究
王丽
(西北工业大学 理学院, 陕西 西安 710072)
脉冲微分方程对在瞬时干扰下状态发生突然变化的演变过程提供了一种自然的描述,关于该类方程的基本理论可参考文献[1]。周期解理论是脉冲微分方程理论中的重要分支[2],Mawhin延拓定理则是研究脉冲微分方程周期解存在性的一种有利工具[3-4]。事实上,Mawhin延拓定理也常被用来研究其它类型微分方程周期解的存在性,例如:泛函微分方程[5],Lienard型方程[6],P-Laplacian方程[7]等等,限于篇幅,此处不一一赘述。
2008年,谢毅、李宪高教授在文献[8]中首次利用Mawhin延拓定理证明了一类单种群模型的概周期解的存在性。随后,J O Alzabut等人延续文献[8]的思路,利用Mawhin延拓定理证明了一类Logarithmic 种群模型的概周期解的存在性[9]。本文作者在文献[10]中通过研究逐段连续的概周期函数性质,将Mawhin延拓定理应用到了证明带脉冲的一类种群模型的概周期解的存在性上。到目前为止,还未发现有文献利用Mawhin延拓定理研究方程的渐近概周期解的存在性。事实上,渐近概周期作为概周期的一种推广,具有重要的实际意义及研究价值[11],鉴于此,本文将利用Mawhin延拓定理研究一类脉冲扰动下的种群模型的严格正的渐近概周期解的存在性。显然,本文具有一定的创新性。除此之外,本文结论部分也说明了,本文的主要结果是已有相关结果的推广。
1 预备知识
在这一节我们将给出一些预备知识,为后面主要结论的证明做准备。首先要注意到的是,脉冲方程的解是分段连续的,所以,区别于Bohr意义下连续的渐近概周期函数[12](这类函数的全体组成的空间用AAP(R)表示),本文首先给出分段连续的渐近概周期函数定义,令PC(R,R)表示全体从R到R的具有第一类间断点tk并在tk处左连续的分段连续函数全体。



注1分段连续的渐近概周期函数定义2是Bohr意义下连续的渐近概周期函数定义[12]的推广。

本文主要研究一类带脉冲的种群模型:
(1)
进一步的,假设方程(1)中参数满足如下条件:
(H1)a(·),b(·),d(·)∈AAP(R),τ(·)∈AP(R),b(·),d(·)的概周期部分b1(·),d1(·)非负,{ck}是概周期序列,{tk} 是一致概周期序列;
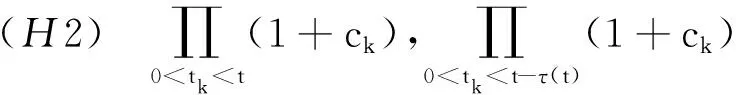
在开始研究方程(1)的严格正的渐近概周期解的存在性之前,我们首先考虑方程:
注意到条件(H2),类似于文献[10]可知,方程(1)和(2)的解有如下关系:
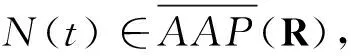
令y(t)=ex(t),则x(t)满足方程:
显然,若方程(3)存在AAP(R)解,则方程(2)存在严格正的AAP(R)解。结合引理3可知,为了证明方程(1)存在严格正的渐近概周期解,只需证明方程(3)的Bohr意义下的渐近概周期解的存在性。本文用到的方法Mawhin延拓定理可参见文献[4-10,13],为节省篇幅,此处省略不提。
2 论证过程
在这一节,我们将利用Mawhin延拓定理证明方程(3)的渐近概周期解的存在性。为此,我们首先令:
此处,α1,α,M是给定的正常数,F(·)是给定的概周期函数,令X=X1⨁X2,Z=Z1⨁Z2,对任意的φ∈XorZ,定义||φ||=supt∈R|φ(t)|,则有:
引理4X和Z均是Banach空间。

接下来我们定义一些Mawhin延拓定理中涉及的算子,令:
则,我们有:
引理5L是指标为0的Fredholm算子且P,Q连续,ImL=KerQ,ImP=KerL。


那么
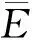
接下来,我们给出本文的主要结论:
定理6假设条件(H1)~(H3)成立,那么,方程(1)存在严格正的渐近概周期解。
证明:从上面的分析可知,为了证明方程(1)存在严格正的渐近概周期解,只需要证明方程(3)的Bohr意义下的渐近概周期解的存在性。定义:J:ImQ→KerL是个恒等算子,为了应用Mawhin延拓定理证明方程(3)的Bohr意义下的渐近概周期解的存在性,我们接下来需要寻找合适的延拓定理中提及的有界开子集Ω。对任意λ∈(0,1),方程Lx=λNx意味着:
(4)
如果x(·)是方程(4)的解,我们对方程(4)两边取平均极限值,可得:
因此
从而可得
由此可以断言,一定∃t*∈R, s.t.|x(t*)| 注意到x(·)是方程的解,其概周期部分记为x1(·)满足方程: 基于上面的不等式,我们立刻可得: 取 类似[8,10]可知此时Ω满足Mawhin延拓定理的所有条件,根据该定理可知方程(3)存在渐近概周期解,从而方程(1)存在严格正的渐近概周期解。证毕。 Mawhin延拓定理之前被广泛用于证明各类微分周期解或概周期解的存在性,本文用该定理证明了一类脉冲种群模型的渐近概周期解的存在性,因此,本文具一定的创新性。 利用Mawhin延拓定理,文献[8]研究了当ck=0时方程(1)的Bohr意义下的概周期解的存在性;文献[10]研究了方程(1)的概周期解的存在性。本文研究了方程(1)的渐近概周期解的存在性,根据文献[12]可知,此时方程一定存在概周期解,故本文的结论推广了已有文献的结论。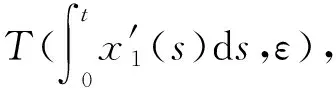
3 结 论

