具有时滞的复值微分系统的概周期解

方聪娜

(集美大学理学院，福建 厦门 361021)

0　引言

众所周知，泛函微分系统广泛应用于各个领域，如核物理学、电路信号处理、生态系统、神经网络、流行病学、化工循环系统等。许多学者致力于研究实值泛函微分系统并且取得了丰富的研究成果[1-7]。但是在诸多应用领域中，实值微分系统也有一定的局限性，如在电子信息工程领域，人们就需要处理复数数据，因此，复值泛函微分系统自然而然地被提出来。近年来，一些学者主要研究了复值泛函微分系统的稳定性及周期性的问题，特别是关于复值神经网络的研究取得了一定的成果[8-11]。从目前来看，对于复值微分系统概周期解的相关问题的研究很少，而概周期解比周期解更具有一般性，所以研究复值微分系统的概周期解具有一定的理论意义和实用价值。本文将复值微分系统分离成实部和虚部，研究了一类具有时滞的复值泛函微分系统的概周期解，得到了保证该系统存在唯一的概周期解的充分条件。

1　相关引理

定义1对于复值函数z(t)=x(t)+iy(t)(x(t)=Re(z(t)),y(t)=Im(z(t)))，若x(t),y(t)都是概周期函数，则称z(t)为概周期函数。

考虑如下概周期系统

x′(t)=A(t)x(t),

(1)

和

x′(t)=A(t)x(t)+k(t),

(2)

这里A(t)是t的概周期函数矩阵，k(t)是t的概周期函数向量。设X(t)是系统(1)的基本解矩阵。

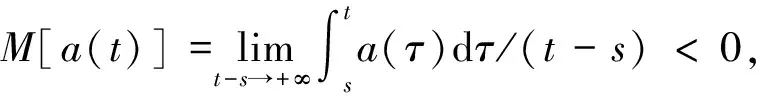
2　主要结果及其证明

本文研究复值微分系统

Z′(t)=A(t)Z(t)+B(t)f(Z(t))+D(t)g(Z(t-τ))+H(t),

(3)

其中Z(t)=(z1(t),z2(t),…,zn(t))T∈Cn,A(t)=(aij(t))n×n∈Rn×n,B(t)=(bij(t))n×n∈Cn×n,D(t)=(dij(t))n×n∈Cn×n,H(t)=(h1(t),h2(t),…,hn(t))T∈Cn,τ>0为时滞，A(t)、B(t)、D(t)都是t的概周期函数矩阵，H(t)是t的概周期函数向量，f(Z(t))=(f1(z1(t)),f2(z2(t)),…,fn(zn(t)))T∈Cn,g(Z(t-τ))=(g1(z1(t-τ)),g2(z2(t-τ)),…,gn(zn(t-τ)))T∈Cn,zj(t)=xj(t)+iyj(t),xj(t)=Re(zj(t)),yj(t)=Im(zj(t))，fj(zj(t))=fjR(xj(t))+ifjI(yj(t)),fjR(xj(t))=Re(fj(zj(t))),fjI(yj(t))=Im(fj(zj(t))),gj(zj(t-τ))=gjR(xj(t-τ))+igjI(yj(t-τ)),gjR(xj(t-τ))=Re(gj(zj(t-τ))),gjI(yj(t-τ))=Im(gj(zj(t-τ))),fjR(·)，fjI(·),gjR(·)，gjI(·)为连续函数，j=1,2,…,n。

令x(t)=(x1(t),x2(t),…,xn(t))T∈Rn,y(t)=(y1(t),y2(t),…,yn(t))T∈Rn；B(t)=BR(t)+iBI(t),BR(t)=(bijR(t))n×n,bijR(t)=Re(bij(t))，BI(t)=(bijI(t))n×n,bijI(t)=Im(bij(t))；D(t)=DR(t)+iDI(t),DR(t)=(dijR(t))n×n,dijR(t)=Re(dij(t))，DI(t)=(dijI(t))n×n,dijI(t)=Im(dij(t))；H(t)=HR(t)+iHI(t),HR(t)=(h1R(t),h2R(t),…,hnR(t))T,hjR(t)=Re(hj(t))，HI(t)=(h1I(t),h2I(t),…,hnI(t))T,hjI(t)=Im(hj(t))；fR(x(t))=(f1R(x1(t)),f2R(x2(t)),…,fnR(xn(t)))T，fI(y(t))=(f1I(y1(t)),f2I(y2(t)),…,fnI(yn(t)))T；gR(x(t-τ))=(g1R(x1(t-τ)),g2R(x2(t-τ)),…,gnR(xn(t-τ)))T，gI(y(t-τ))=(g1I(y1(t-τ)),g2I(y2(t-τ)),…,gnI(yn(t-τ)))T，则系统(3)可化为如下实值系统

(4)

则方程(3)存在着唯一的概周期解。

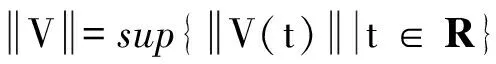
对任意的V=(v1,v2)∈G,现在考虑如下的概周期微分系统

(5)

由条件1)及引理2可知,系统(5)存在唯一的概周期解XV(t)=(xV(t),yV(t))T,它可表示为

(6)

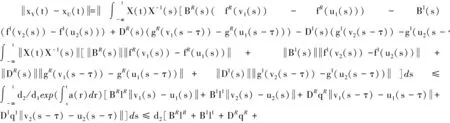
(7)

直接由式(7)的两边同时对t求导即知，(φ(t),φ(t))T是方程(4)的唯一概周期解，从而方程(3)存在唯一的概周期解。